冻融砂岩的能量演化规律与损伤本构模型

高红梅， 李洪伟， 徐 立， 杨 帆

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

岩石作为一种典型的非均质各向异性材料，普遍存在于工程实际中，由于岩石所受荷载极其复杂，加之构成岩石的颗粒分布极端不均匀，导致岩石的本构曲线呈非线性特征[1]。在我国的北方寒区，岩石在自然界中受到冻融循环的影响，冻融循环作用会加大岩石内部初始缺陷(节理、微裂纹、孔隙)的扩展速度，加剧岩石的内部损伤，弱化岩石本身的力学性能[2]。基于热力学定律发现，自然界中物质的破坏实际上是由物质内外部能量变化引起的，可以说是一种原有稳定状态失衡现象，因此，从能量角度出发，研究冻融砂岩变形破坏过程能量的演化规律，对岩石开采和冻融灾害的研究有重要的现实意义。

国内外诸多学者开展了岩石能量与本构关系的研究，杨科等[3]通过分离式霍普金森压杆(SHPB)实验系统加载煤样，得出试样在整个破坏过程中能量与含水率的变化规律。秦涛等[4]给出了在不同围压下岩石试件能量演化与特征应力、裂纹发展等之间的规律。苗胜军等[5]通过对特殊地区岩石三轴循环加卸载实验研究，获得各种能量与含水率之间的变化规律。Dougill等[6]指出损伤理论作为探索岩石的理论基础。谢和平等[7]应用耗散能理论，构建了岩石损伤演化模型，给出了基于损伤理论的本构关系。张树光等[8]采用最小耗能原理及应变等效原理建立了岩石损伤方程和非线性的蠕动方程。刘文博等[9]对饱和砂岩进行常规力学压缩实验，结合能量原理得出适用于水岩耦合下砂岩破坏准则。孙清佩等[10]以统计损伤理论作为理论依据，结合耗能原理建立了砂岩的损伤本构模型。张尧等[11]从能量角度推导了损伤应力-应变函数，以此建立基于能量耗散的岩石损伤本构模型。邓华峰[12]通过砂岩的单轴加卸载实验，获得损伤变量、残余应变和各种能量的演化规律。林大超等[13]基于Mohr-Coulomb准则，给出了一种估算岩石压缩强度的方法。郎东明等[14]分析冻融损伤对岩石试样的变形以及力学性能影响，建立了岩石损伤本构模型。

目前，以能量法为理论基础对岩石损伤破坏机理的研究，主要集中在岩石本构模型的构建和能量演化规律的探究，笔者结合冻融岩石的损伤破坏特性与能量演化特征，依据热力学定律和能量耗散定律，结合砂岩的单轴压缩实验，研究冻融砂岩在加载过程中的能量演化规律及损伤演化机理，为解决冻融岩石开采等实际问题提供理论依据。

1 实 验

1.1 冻融循环实验

文中所选红砂岩均采自山东地区，将所取红砂岩制作成直径为50 mm，高为100 mm的圆柱体粗砂岩试块，共12块，3个砂岩试块为一组，共4组，设置冻融循环次数分别为0、10、35和50次，实验砂岩如图1所示。在冻融循环前将砂岩进行饱和处理，冻融循环实验采用冻融实验机，调节冻融实验机的温度保持在-20～20 ℃之间。

图1 砂岩试样Fig. 1 Sandstone sample

1.2 单轴压缩实验

采用伺服万能实验机对冻融后的砂岩进行单轴压缩实验，以速率为0.01 mm/s的位移加载方式加载。砂岩的单轴压缩应力-应变曲线如图2所示。

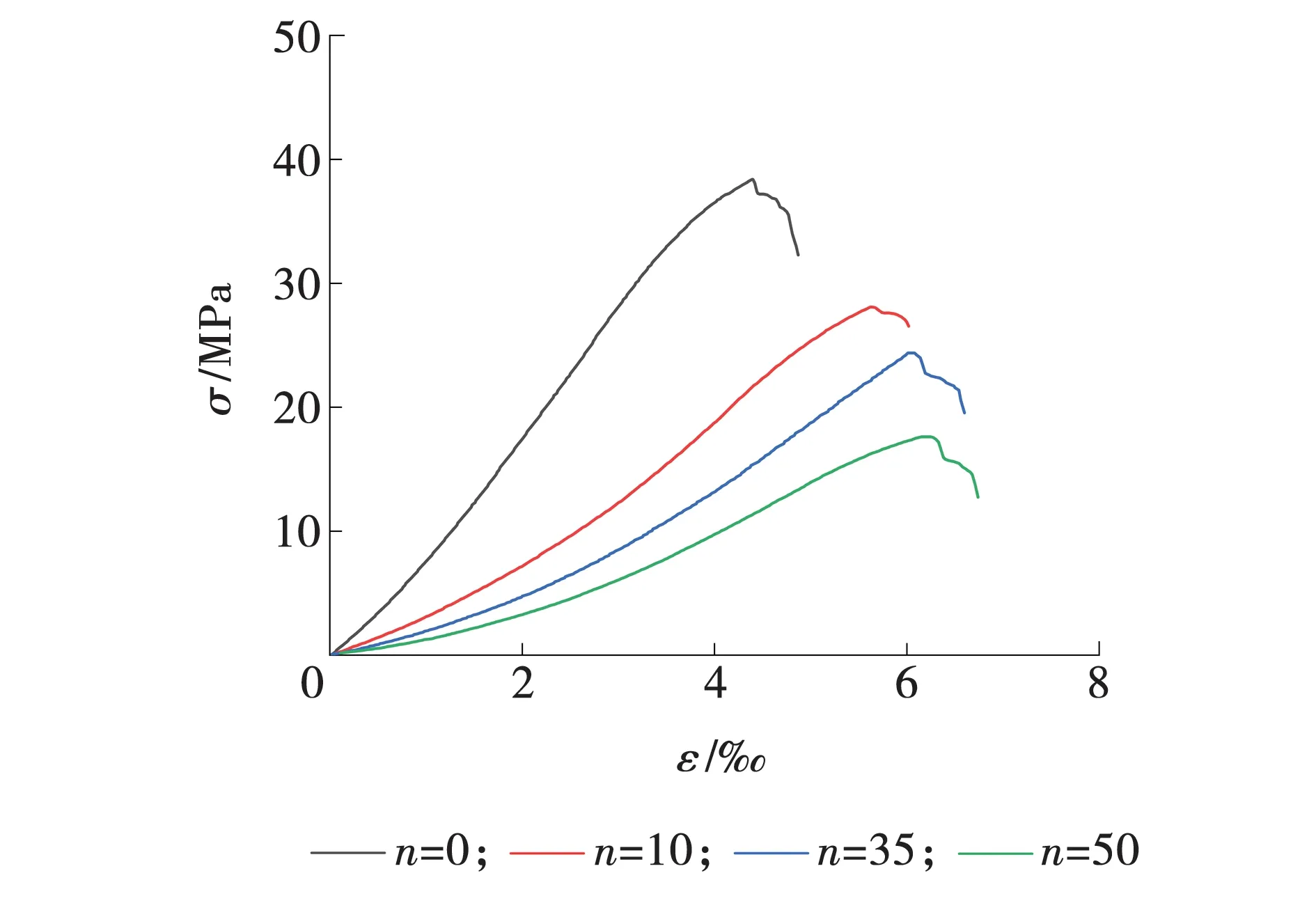
图2 砂岩的单轴压缩实验曲线Fig. 2 Uniaxial compression test curve of sandstone

由图2可知，随着冻融次数的增加，砂岩的强度逐渐降低，曲线也越来越平缓。砂岩的初始孔隙会随着砂岩冻融损伤的增加而增加，增加的速率在不同冻融次数下有所不同[15]。孔隙度增大的主要原因是冻融循环使岩隙中的水反复结晶和融缩致使裂纹不断发展，新的裂纹不断发育[16]。不同冻融次数下的砂岩的力学参数，如表1所示。其中，砂岩冻融次数为n，峰值强度为σf， 峰值应变为εf，弹性模量为E。

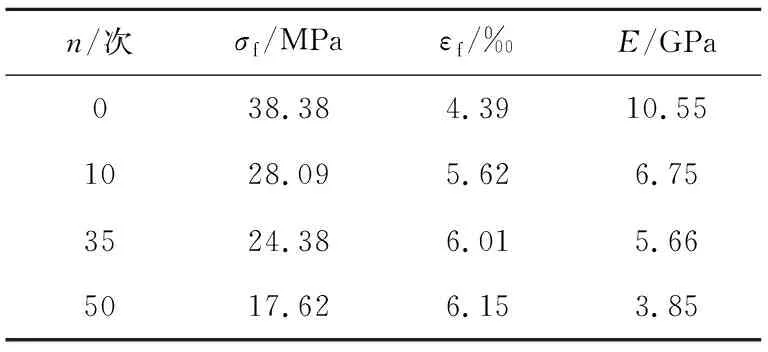
表1 砂岩力学参数

由图2和表1可知，砂岩强度随冻融次数的增加而降低，弹性模量整体上也呈现逐渐降低的趋势，峰值应变出现逐渐加大的变化。与冻融0次的砂岩相比，冻融50次的砂岩强度损失54.09%，弹性模量下降63.51%。冻融10次与0次相比强度损失了26.81%，而冻融35次与0次相比只降低了36.4%，说明前10次冻融造成的损伤大于10次到35次的损伤。表1中砂岩的强度、弹性模量与冻融循环次数之间存在着函数关系，采用指数函数在砂岩的强度参数与冻融次数建立函数关系，结果如图3所示。

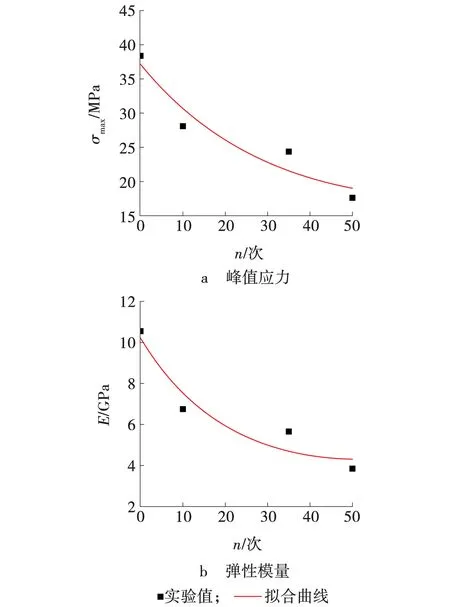
图3 岩石强度参数与冻融次数的关系Fig. 3 Relationship between rock strength parameters and freeze-thaw times

2 冻融砂岩的能量分析

2.1 能量计算原理

由热力学定律可知，假定系统与外界环境无热量交换，外力对砂岩系统所做的功一部分转化为弹性能，一部分转化为耗散能，若考虑残余应变和滞后效应，还有一部分转化为储存在砂岩内部的储存能。砂岩的能量计算公式为

U=Ud+Ue+Us,

(1)

式中：U——输入的总能量；

Ud——耗散能；

Ue—— 弹性应变能；

Us—— 储存能。

依据式(1)能准确计算砂岩的耗散能。由实际的单轴循环加卸载曲线可知，砂岩滞回环曲线是不闭合的，存在着滞后效应，还存在一部分的输入能以储存能的方式存在于砂岩中。在加载的过程中该部分能量同弹性能一样在砂岩内部持续积累，在卸载阶段，弹性能会从砂岩内部逐渐向外界释放，然而该部分能量即未释放，也未耗散，而是永久的储存在砂岩的内部[17]，但为了计算方便，往往忽略此部分的能量。修正后的能量计算公式为

(2)

式中：σi—— 砂岩的三个主应力，i=1,2,3；

当采用单轴实验加载时，σ2=σ3=0，此时，式(2)变为

(3)

2.2 砂岩的能量演化规律

砂岩的总能量为应力-应变曲线与应变轴所围成的面积，弹性能可由式(3)求得，总能量与弹性能的差值为砂岩的耗散能。砂岩能量计算结果如图4所示。

由图4可知，随着加载实验的进行，三种能量曲线整体上呈现上升的趋势，达到峰值应变之前，输入砂岩的总能量增长最快，弹性能其次，耗散能增长最缓慢[18]。在压密阶段，弹性能和耗散能增长较慢，此时，输入的能量主要用于砂岩内部结构的不可逆形变；在弹性阶段，输入的总能量绝大部分转化为弹性能储存在砂岩中，弹性应变能增长的速度明显大于耗散能增长的速度，说明此阶段输入砂岩内部的能量主要以弹性应变能的方式储存在砂岩结构中。从图4c可以看出，不同冻融次数下砂岩的耗散能都会呈现一个先增加到一个稳定的水平，然后再持续增加，冻融0次与10次增加的趋势最明显，表明在整个加载过程中砂岩一直以产生不可逆变形的方式消耗能量，加载前期与达到峰值应变时不可逆变形的速率比弹性阶段的增长速率快。

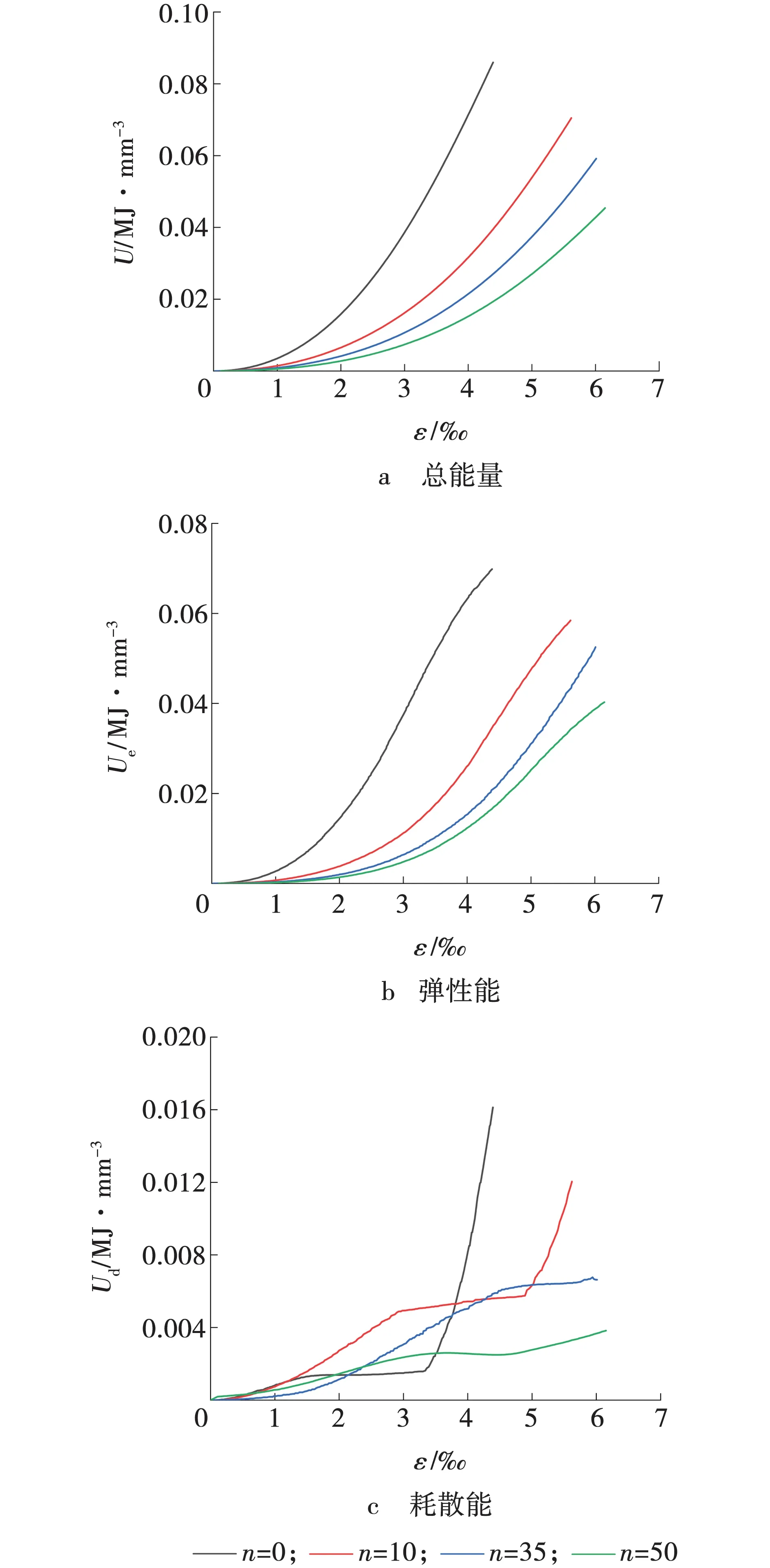
图4 砂岩能量变化Fig. 4 Energy change of sandstone

由表2和图4可见，砂岩总能量在冻融0次时为0.085 97 MJ/mm3，当冻融10次为0.070 48 MJ/mm3，当冻融35次时为0.059 16 MJ/mm3，当冻融50次时为0.045 41 MJ/mm3。与冻融0次相比，总能量在砂岩冻融10、35和50次时的总能量分别降低了18%、31.2%和47.18%。随着冻融次数的增加，极限弹性应变能出现逐渐下降的趋势，冻融50次与冻融0次相比下降了42.32%；耗散能也出现了逐渐降低的趋势，由冻融0次的0.016 13 MJ/mm3下降到冻融50次的0.005 13 MJ/mm3，降低了68.2%，整个变形破坏过程实质上是能量耗散与能量转化的综合表现[19]。由图4b可知，冻融循环作用会降低砂岩储存能量的能力，使砂岩在外荷载的作用下更易达到材料的储能极限，最终导致砂岩的开裂破坏。

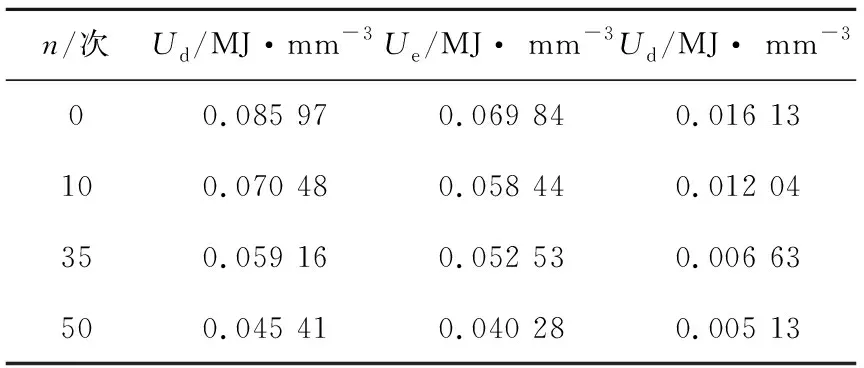
表2 砂岩能量特征值

3 砂岩的冻融荷载本构模型

3.1 砂岩的冻融损伤变量

冻融循环作用会弱化试样的力学性能，降低材料的弹性模量。随着冻融次数的增加，岩石的各种力学性能变弱[20-21]，内部裂纹增加[22-23]，因此,通常采用弹性模量定义冻融损伤变量[24]为

(4)

式中：E0——未冻融时的弹性模量；

En——冻融n次时的弹性模量；

Dn——岩石的冻融损伤变量。

由表2可知，冻融循环作用会降低砂岩储存能量的能力，使砂岩在外荷载的作用下更易达到材料的储能极限。外界能量的输入导致砂岩内部的损伤加剧，此过程伴随着能量的耗散，因此，可用耗散能定义损伤变量为

(5)

式中：a、b——与材料有关的参数，通过式(5)拟合获得；

Udf—— 0次冻融时的峰值耗散能；

Udfn—— 冻融n次的峰值耗散能。

3.2 砂岩的荷载损伤变量

由于砂岩颗粒大小的不均匀性和分布的随机性导致砂岩的各向异性，内部初始缺陷的存在导致其强度值也是随机变化的，故可采用Weibull分布函数表示砂岩材料的微元体破坏的统计分布为

(6)

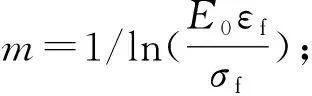
λ—— Weibull分布参数。

引用张慧梅[24]中损伤变量与分布函数的关系为

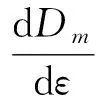
(7)

由式(6)和(7)可得：

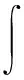
(8)

式中：ε——材料应变；

εf——峰值应力σf所对应的应变值。

冻融与荷载共同作用的损伤变量计算公式为

1-Dnm=(1-Dm)(1-Dn)，

(9)

式中，Dnm——冻融受荷总损伤变量。

将冻融损伤变量与荷载损伤变量代入式(9)可得总损伤变量为

(10)

由式(7)、(10)可知，总的损伤分为两部分，分别为冻融损伤与受荷损伤，两者相互约束、相互影响，可较真实的反应冻融砂岩的损伤破坏规律。

根据损伤力学的基本关系[25]有：

σ=E(1-D)ε，

故冻融荷载损伤耦合作用下岩石的本构方程为

(11)

4 砂岩本构模型的验证

由式(5)可知，结合表1可拟合得参数a、b的值分别为0.944 4与0.797 45，且R2=0.907 1。拟合结果如图5所示。

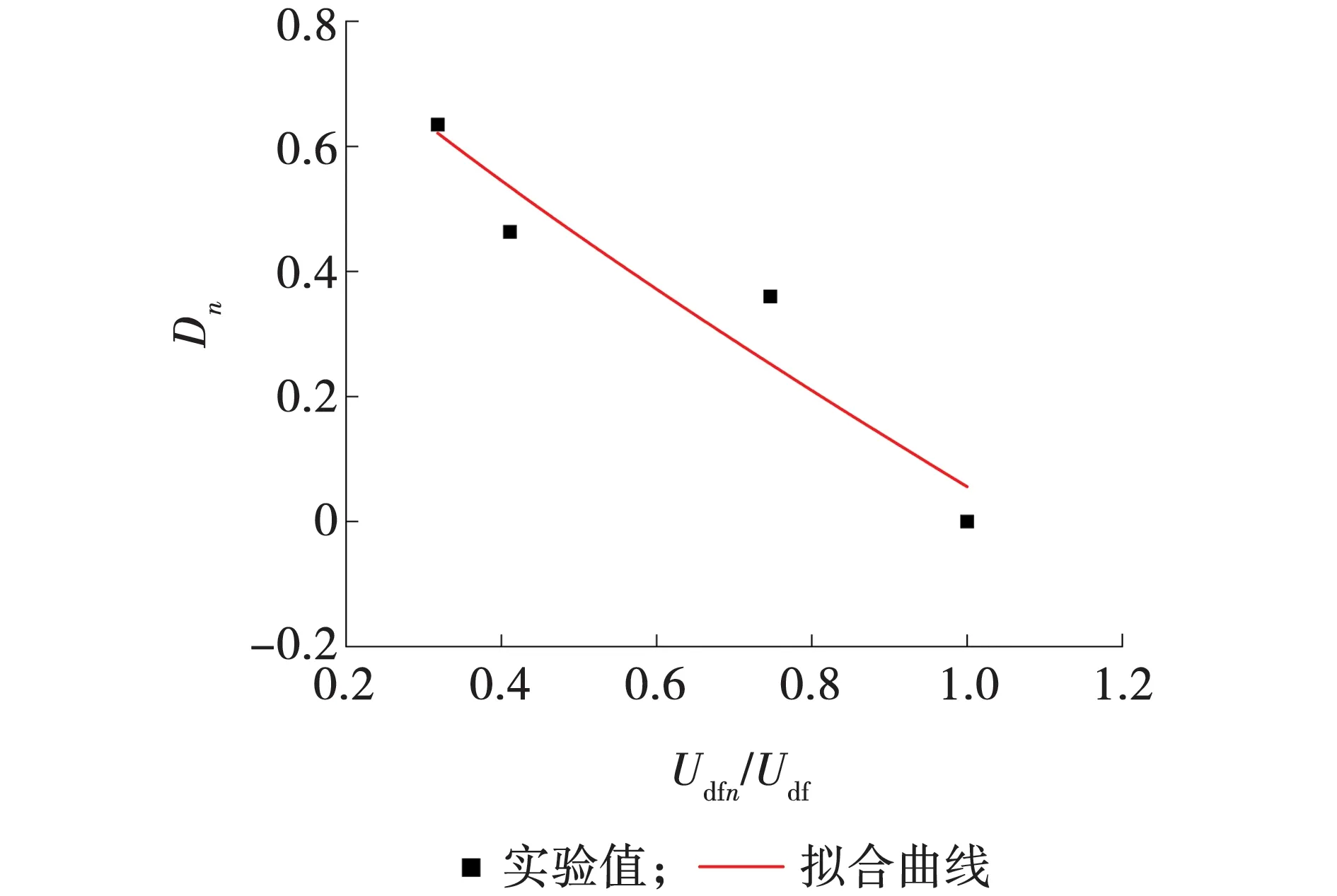
图5 耗散能比与冻融损伤变量关系Fig. 5 Relationship between dissipation energy ratio and freeze-thaw damage variable

利用式(10)依据不同冻融次数条件下的单轴压缩实验数据，获得不同冻融次数下应变与总损伤变量关系，如图6所示。

由图6可知，在应变为0时，不同冻融次数下的冻融损伤不同，冻融0次曲线从坐标原点出现，表明其没有冻融损伤仅发生荷载损伤。冻融10、35和50次曲线皆存在冻融损伤，且曲线出发点分别为0.25、0.54和0.62，表明砂岩的冻融次数越多，冻融损伤就越大。随着加载实验的增加，岩石所受荷载损伤越来越大，直至应变达到9‰时，损伤变量接近1，表明试样已几乎开裂破坏。有冻融损伤与无冻融损伤曲线相比，前者由于有冻融损伤的存在，使在发生相同的应变条件下，前者的损伤大于后者的损伤，这与客观事实相符。在相同冻融次数下，随着加载实验的进行，岩石内部的裂纹孔隙等初始损伤不断发育扩展，最后贯通形成宏观上的裂缝，导致岩石的损伤加剧。相同的总损伤变量的条件下，冻融次数多的砂岩发生的变形要小于冻融次数小的变形，因此，其初始冻融损伤程度大，导致更易发生受荷载破坏。

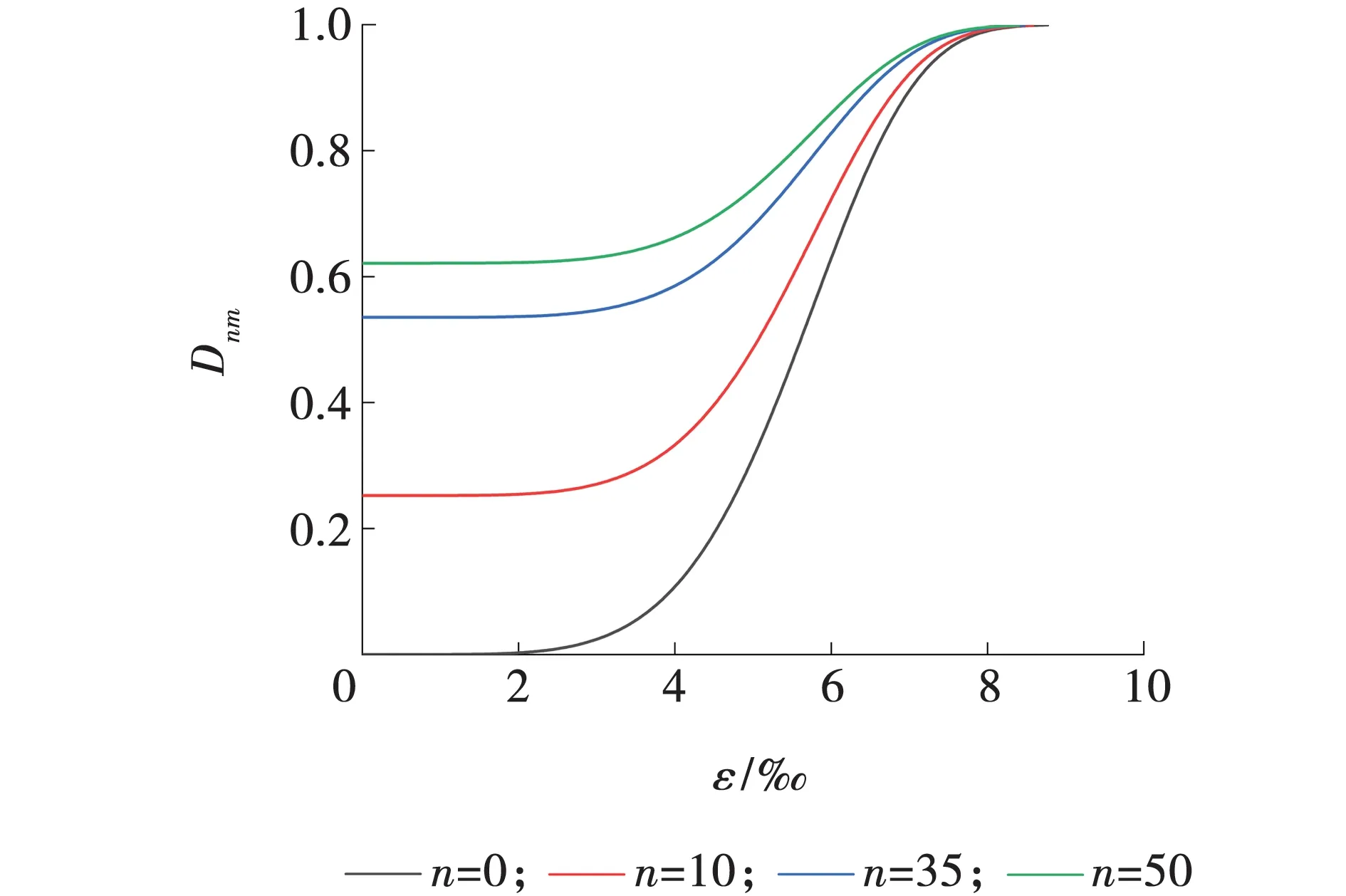
图6 砂岩应变与总损伤变化曲线Fig. 6 Variation curve of sandstone strain and total damage

为研究总损伤演化率与应变之间的关系，由式(9)可得：

(12)

整理式(12)可得：

(13)

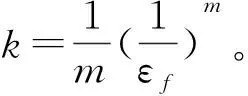
利用实验测得的数据代入式(13)可得，不同冻融循环次数下砂岩的应变与总损伤率的关系如图7所示。

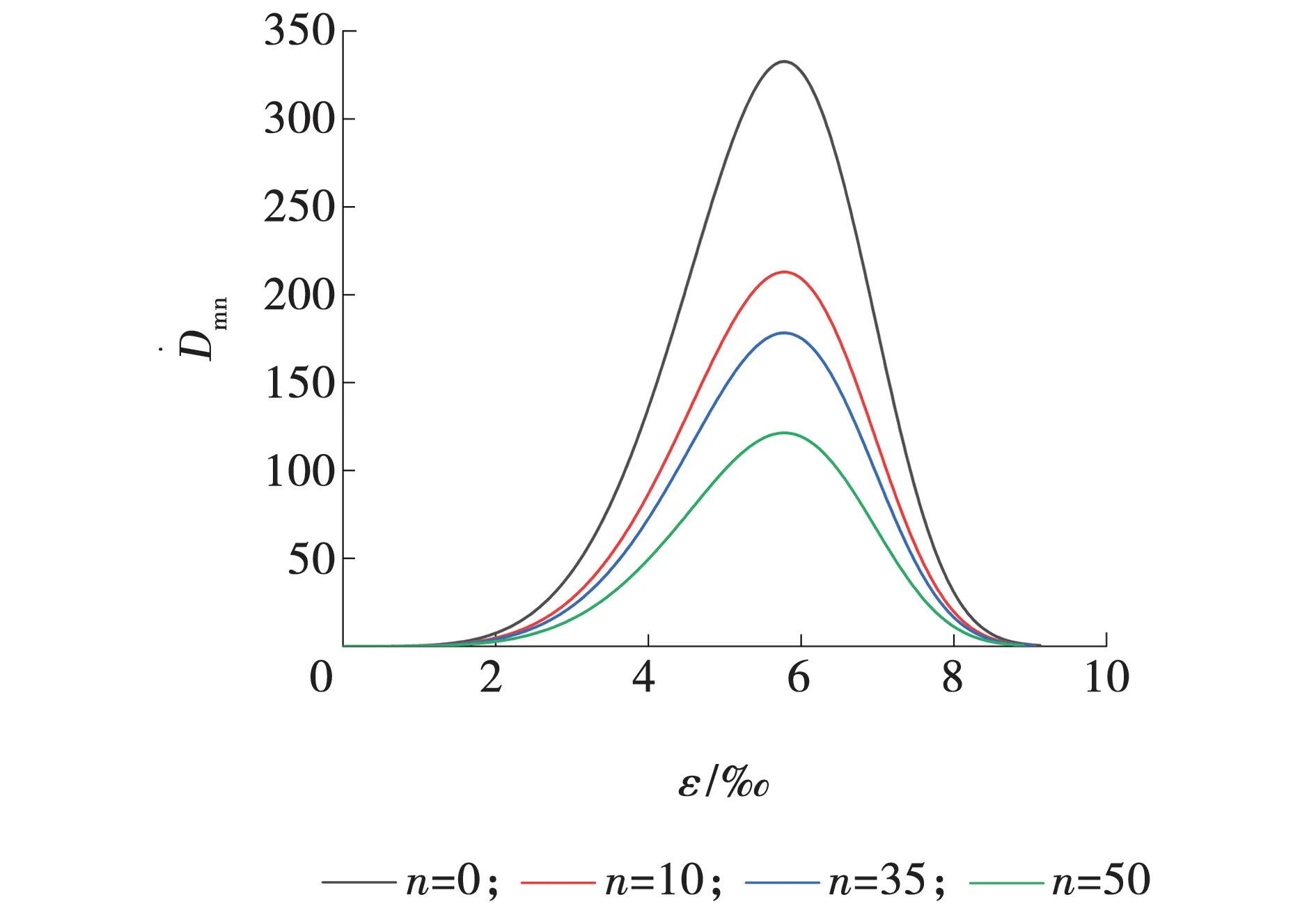
图7 应变与总损伤演化率的关系Fig. 7 Relationship between strain and total damage evolution rate

由图7可知，冻融循环次数不影响总损伤率的变化趋势，仅会影响其数值大小。在相同的应变条件下，随着冻融次数的增加，损伤演化率的数值减小，冻融0次至冻融10次变化最大，冻融10、35和50次变化较稳定。达到峰值损伤变化率之前，上升的趋势较峰后平缓，表明峰前的的脆性小于峰后的脆性。相同冻融次数下，随着应变的增加，总损伤演化率都出现先增加至峰值后降低的趋势，表明在加载的中期阶段(峰值演化率左右)，砂岩内部的损伤达到最大。

5 结 论

通过砂岩单轴压缩实验结果分析了砂岩全过程能量演化规律，结合能量耗散理论和损伤力学原理建立了冻融荷载砂岩本构模型。

(1)砂岩的强度与弹性模量随着冻融次数的增加逐渐降低，冻融循环作用造成的损伤弱化了砂岩的力学性能。与0次冻融相比，冻融50次时弹性模量损失了63.15%，峰值强度损失了54.09%。采用多项式函数拟合了砂岩抗压强度、弹性模量与冻融次数之间的关系，拟合精度良好。

(2)随冻融次数的增加，砂岩的弹性能和耗散能皆呈现出降低的趋势。在峰值应变前，输入的能量主要以弹性能的方式储存在岩样内部，仅有很少一部分能量转化为耗散能，直至达到峰值应变，耗散能的增长速度有所增加而弹性能趋于稳定，表明此时砂岩存储的能量已基本达到材料的储存极限，宏观上表明为砂岩的开裂破坏。

(3)运用耗散能定义冻融损伤，受外荷载损伤假设微元体强度服从Weibull分布，由此构建了冻融损伤与荷载损伤耦合作用的本构模型。冻融荷载耦合总损伤变量与应变存在着明显的非线性特征，冻融与荷载的耦合作用使总损伤弱化。冻融损伤不影响总损伤演化率的变化趋势，只会影响其数值的大小，总损伤演化率峰值后的脆性要大于峰值前的脆性。