一种水上电动飞机支撑结构分级优化方法
赵立杰, 田孟伟, 李景奎
(1.沈阳航空航天大学辽宁省通用航空研究院, 沈阳 110136; 2.沈阳航空航天大学民用航空学院, 沈阳 110136)
随着中国经济的发展对民航运输和通用航空的需求日益增长,新能源电动飞机的出现为航空的彻底绿色化提供了一条光明的技术途径[1]。而针对中国水域众多和土地紧张的国情,发展各种性能优良的水上电动飞机将有广阔的市场[2]。浮筒以及所连的支撑结构作为水上飞机的主要承力结构,在飞机水上降落时会承受巨大冲击载荷,可靠性良好的起落装置对飞机的安全性能有着更好的保障。在概念设计初期,满足传力要求的最优路径是首要任务。
现有拓扑优化的结构参数化和理论研究较多,结构设计方面的应用研究较少。在桁架研究方面多体现在形状优化和尺寸优化,与较高层次的拓扑优化结合较少。Assimi等[3]采用MATLAB开发的改进遗传算法,对平面桁架结构的形状、尺寸和拓扑结构进行优化,使桁架总质量最小。邱福生等[4]针对机翼在实际应用中的气动-结构耦合问题,开发了一种在机翼翼型表面直接加载气动载荷的三维拓扑优化方法。赵立杰等[5]利用对机翼前后缘柔性支撑结构进行了拓扑优化设计。戴一范等[6]以某空间设备支撑结构为例,分析结构材料在设计空间的分布形式和桁架结构的传力路径,获得满足要求的空间桁架结构并进行优化设计。徐皓等[7]基于优化驱动设计的思想,提出了一种分步结构优化方法,应用于卫星的支撑腿结构设计中,实现了多目标的形状尺寸优化方案。苏若斌等[8]针对卫星用复合材料桁架结构,提出一种多级优化设计方法,对复合材料桁架结构的空间构型、几何参数以及材料铺层角度开展协同优化设计。杨丰福等[9]在拓扑优化基础上利用iSight对光纤传像支撑结构,进行了集成优化计算,取得了明显的减重效果。
现以双座电动水上飞机为背景,结合飞机减重的需求和桁架结构特点,对浮筒支架结构进行优化设计。首先基于三维拓扑优化方法对支撑架的包络空间进行迭代计算,得到最优传力构型,得到合理的节点位置和杆件连接方式。接着利用ANSYS和iSight对杆件截面参数进行联合优化,采用多岛遗传算法得到各个截面的最小尺寸;最后通过增加“翼型”整流罩减小杆件的阻力值,降低桁架结构对飞机气动性能的影响。通过提出一种新的浮筒支架总体布局和构型优化方式,旨在为水上飞机支撑架设计提供一种新思路,也为相似的类桁架结构优化提供理论依据和技术支持。
1 三维拓扑优化理论
浮筒支架的结构概念设计主要是在机身与浮筒之间的区域寻找最优传力路径,满足在体积约束下实现结构柔度最小化。三维区域拓扑优化属于连续体优化问题,采用变密度理论中的固体各向同性材料惩罚(solid isotropic material with penalization,SIMP)模型,通过引入中间密度单元,将离散型问题转化成连续型优化问题,而实际上,中间密度单元是无法存在和制造,因此要尽量避免中间密度单元的产生,减少中间密度单元的数目,此时就需要对设计变量中出现的中间密度值进行惩罚[10]。与使用现有优化软件相比,利用MATLAB进行关键代码的修改,可以实现优化区域网格快速定义、边界与载荷条件的设定等,使得规则三维区域寻优过程更加高效简洁。
1.1 材料插值模型
变密度理论的材料插值模型引入中间密度单元,即
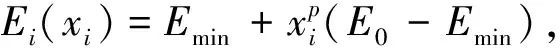
xi∈[0,1]
(1)
式(1)中:Ei为插值后的弹性模量;E0为实体材料的弹性模量;xi为单元相对密度;Emin为孔隙材料的弹性模量,为避免有限元刚度矩阵的奇异性,使其不为0。
改进的SIMP方法与经典的SIMP公式相比具有许多优点,包括材料弹性模量的最小值与惩罚因子之间的独立性。与二维拓扑优化99行方法相比,三维问题也会遇到数值上的困难,如网格依赖性、棋盘化问题和局部最小值。为了缓解这些问题,常见的方法是利用正则化技术引入密度过滤器[11]。
定义一个基本的滤波密度函数,即

(2)
式(2)中:Ni为元素xi积vi的邻域;Hij为权重因子。邻域定义为
Ni={j:dist(i,j)≤R}
(3)
式(3)中:操作符dist(i,j)为元素i的中心到元素j的中心的距离;R为滤波器的大小。例如,权重因子Hij可以定义为相邻元素之间距离的函数,其中j∈Ni。
Hij=R-dist(i,j)
(4)
筛选后的密度定义了一个修改后的物理密度变量,实际上,这里省略了物理密度对设计变量过滤密度的依赖,并且被更新到拓扑优化公式和SIMP模型为
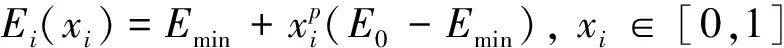
(5)
1.2 有限元分析
1.2.1 平衡方程的建立
根据SIMP方法和广义胡克定律,各向同性单元的三维本构矩阵插值方程为
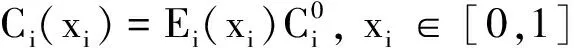
(6)
式(6)中:Ci为具有单位杨氏模量的本构矩阵,单位本构矩阵为
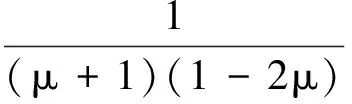
(7)
式(7)中:μ为各向同性材料的泊松比。使用有限元方法,弹性实体单元刚度矩阵是单元本构矩阵Ci与应变位移矩阵B的体积积分,形式为
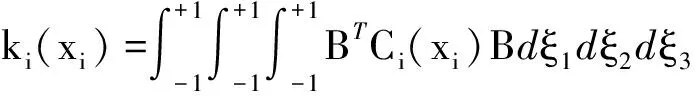
(8)
ξe(e=1,2,3)为图1所示的八节点六面体自然坐标。应变位移矩阵B将应变与节点位移u联系起来。利用SIMP方法,将单元刚度矩阵插值为

(9)

(10)
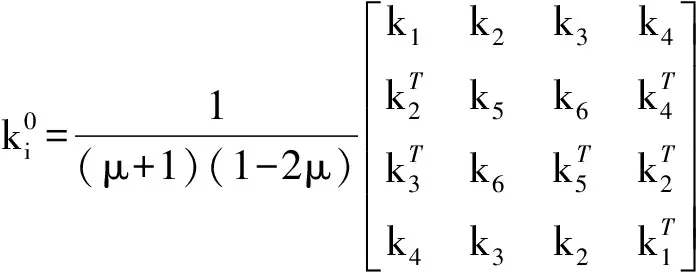
(11)
整体刚度矩阵K通过装配元素级对应的ki得到
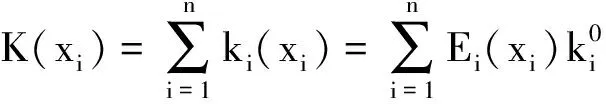
(12)
将插值公式代入得

(13)
最后,节点位移矢量U(x)为平衡方程的解, 其中F是节点力的矢量,即
K(xi)U(xi)=F
(14)
1.2.2 网格离散与编排规则
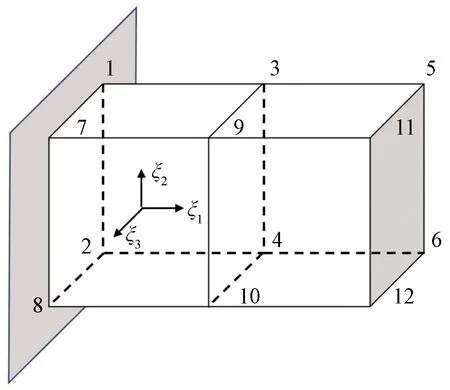
图1 网格离散编排示意图Fig.1 Schematic diagram of grid discrete arrangement
以图1中的离散棱柱结构为例,它由八节点的六面体组成。使用编号标识的节点按从上到下、从左到右和从后到前的顺序排列。每个节点的位置是根据笛卡尔坐标系定义的,原点在左上后角。在每个元素中,8个节点N1~N8按逆时针方向排列。通过给定体积的大小(nelx×nely×nelz)和节点N1(x1,y1,z1)的全局坐标,通过映射关系可以识别该单元中其他7个节点的全局节点坐标和节点ID。每个元素的节点ID被集成在一个连接矩阵中,大小为nele×24,24代表每个单元具有24个自由度,连接矩阵会被装配到总刚度矩阵中。
1.3 优化问题的描述
最小柔度问题的目标是找出在规定的支撑和荷载条件下,使结构变形最小的材料密度分布x。结构的最小柔度被定义为
c(x)=FTU(x)
(15)
三维结构在体积约束下的最小柔度优化问题为

(16)

1.3.1 灵敏度分析及计算
体积分数、柔度对设计变量的导数分别为

(17)
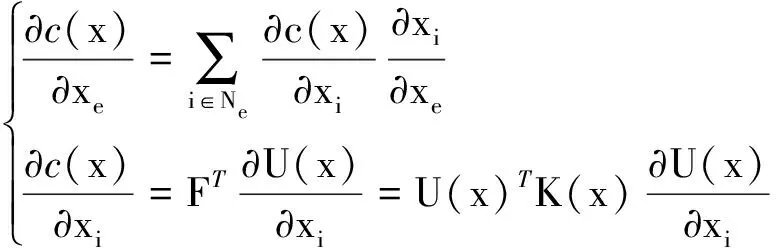
(18)
将插值公式(13)和平衡方程(14)代入式(17)、式(18)可得
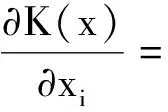
(19)
最终可得
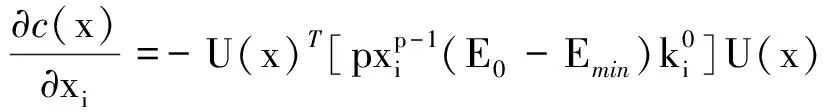
(20)
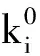
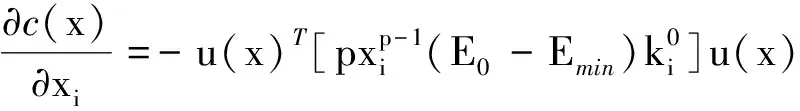
(21)

1.3.2 优化算法
这里只考虑了单目标函数与单约束条件下问题的求解,采用收敛速度较快的优化准则法。其特点为计算规模与求解变量无关,推导过程简单直观,拥有较快的收敛速度。OC算法的制定基于以下条件:
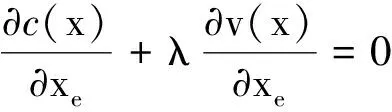
(22)
如果约束0≤x≤1处于非活动状态,则当k=1,2,…,n,满足KKT条件时就可以实现收敛,其中λ为与约束v(x)相关的拉格朗日乘数。该最优条件可以表示为Be=1,
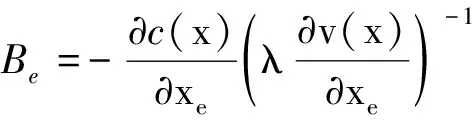
(23)
更新方案
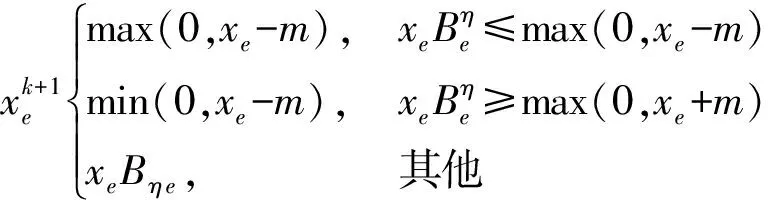
(24)
式(24)中:m为正移动极限;η为数字阻尼系数。对于最小的依从性问题,建议选择m=0.2和η=0.5。具体流程如图2所示。
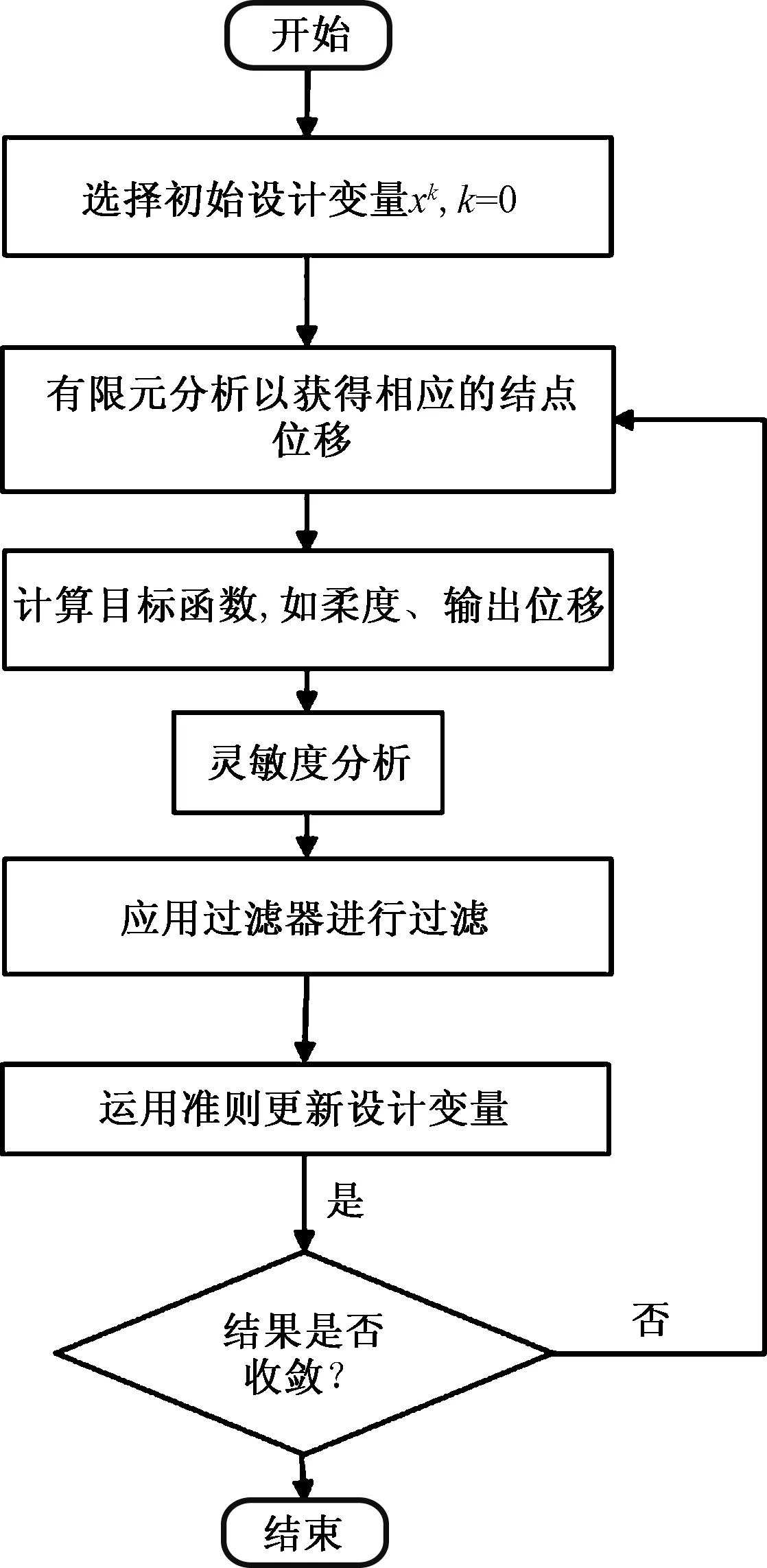
图2 OC算法流程Fig.2 OC algorithm flow chart
1.4 边界条件和载荷条件
考虑飞机静态设计载荷要求,支撑结构主要承担机身纵向载荷,现有飞机载荷600 kg,在浮筒与机身之间的包络空间(图3中蓝色区域)作为设计区域,以现有浮筒尺寸和支撑点位置,确定依旧采用4点传力的方式。对支撑架模型简化设计,将主要载荷施加在上表面前后主要受力集中点,包络空间底部4点为固支约束。
对设定好的有限元模型进行迭代计算,得到如图4所示的较为清晰的结构骨架。由图4可知,支撑架的主要传力路径由4根主支撑和8根副支撑组成。

图3 设计区域包络图Fig.3 Design area envelope

图4 结构骨架Fig.4 Structural skeleton
2 ANSYS和iSight的联合尺寸优化
iSight是功能强大的计算机辅助优化平台,广泛应用于航空航天汽车领域的零部件、子系统优化,以及复杂产品的多学科优化设计。用户可以通过iSight集成和管理复杂的仿真流程,运用多种优化算法自动探索得到优化方案,从而缩短研究周期,降低研发成本[12]。优化流程如图5所示。
2.1 桁架骨架建模
对拓扑结果进行提取,可以得到16节点的桁架结构,在ANSYS中利用APDL语言建立支撑结构桁架有限元模型(图6)。在极限载荷下进行有限元分析,得到最大应力,作为后续设计的约束条件。在有限元基础上利用iSight优化软件对各个杆件的截面尺寸进行详细优化设计。考虑到支撑架抗压抗弯的力学要求和减重的需求,初步设计截面采取管状截面。首先对桁架结构进行参数化编写,对桁架结构进行简化编码,包括材料单元设置、各个杆件的截面定义、节点与杆件的连接、网格的划分、载荷与约束的施加,并将结果输出制作ansys.bat文件。
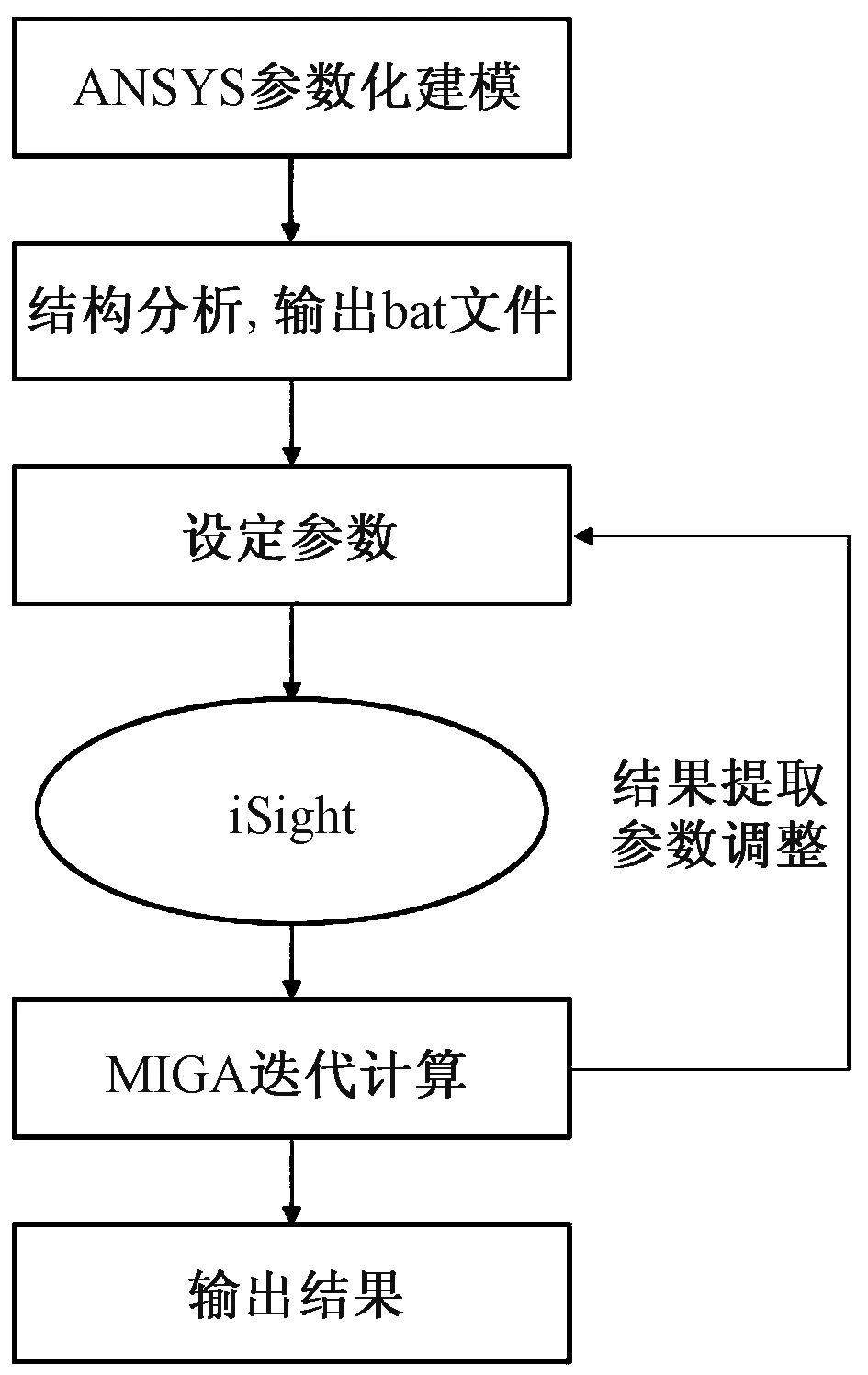
图5 联合优化流程图Fig.5 Joint optimization flow chart
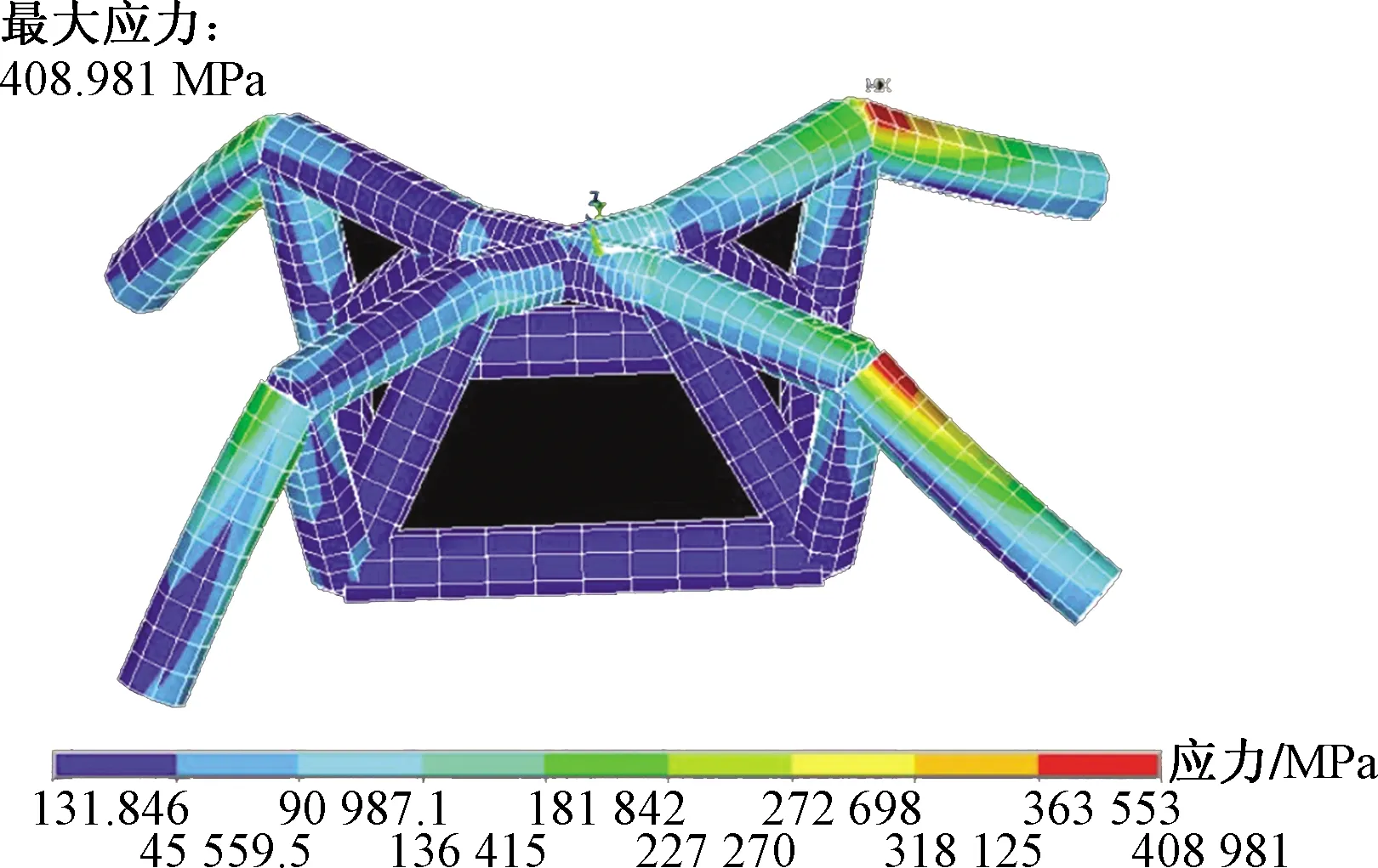
图6 ANSYS建模Fig.6 ANSYS modeling
由图6可知,最大应力在材料的弹性变形范围内,出现在机身后部支撑杆位置,基本符合水上飞机重心在断阶位置的要求;最大受压应力为408.981 MPa,低于材料的许应力550 MPa,符合强度设计要求。
2.2 iSight集成优化计算
基于iSight的优化设计计算流程如图7所示,主要由遗传算法优化组件、ANSYS结构设计组件、数据交换组件和质量计算组件构成。
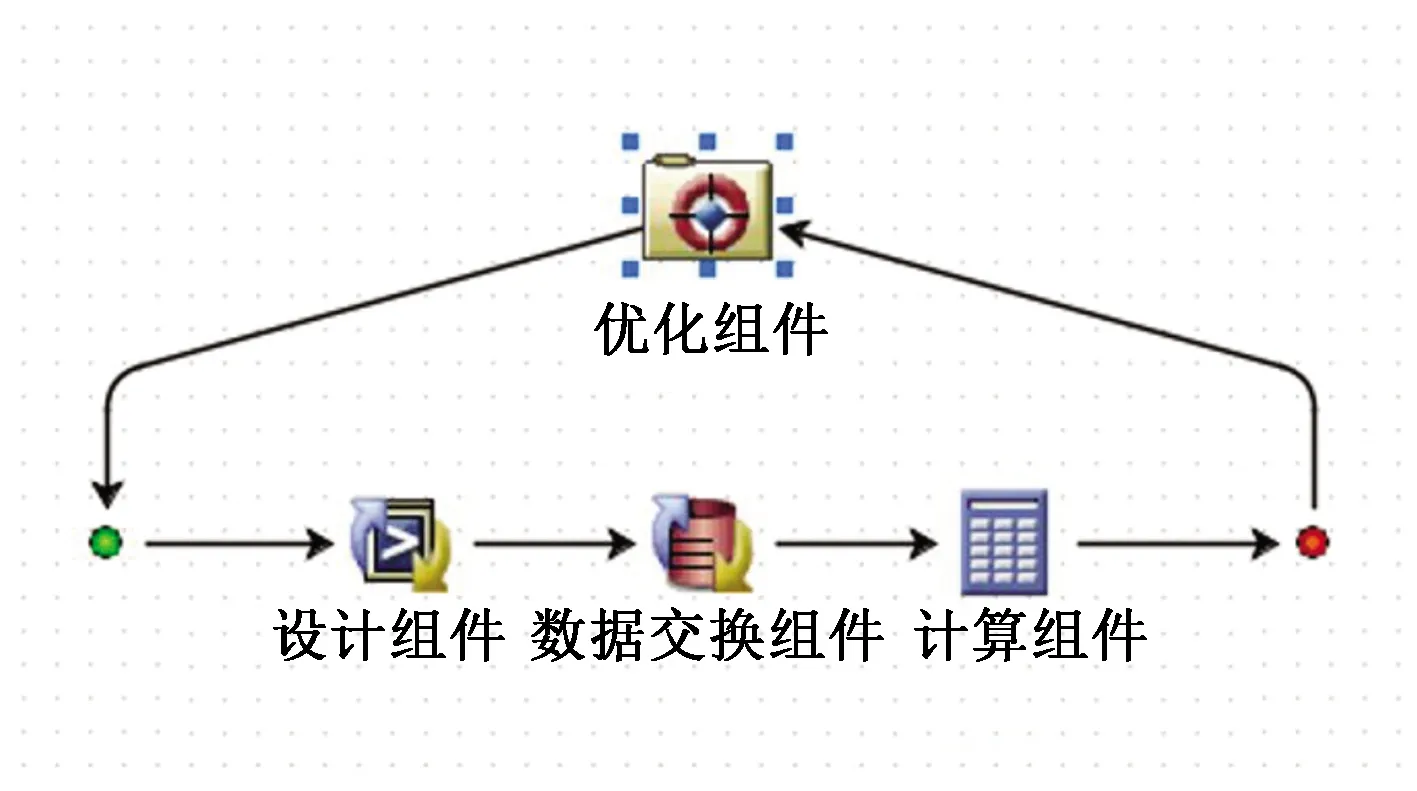
图7 iSight结构设计组件流程Fig.7 iSight structural design component flow
首先通过结构参数化计算,定义设计变量,对横截面a1~a24进行初始化;定义约束条件包括尺寸约束(设定截面面积上下限)和强度约束(优化后的桁架结构所承受的最大应力不得超过材料的屈服应力);所求解目标函数为桁架总质量最小。
优化算法的选择:选用多岛遗传算法,该方法是基于并行分布遗传算法的改进,对于大规模的桁架结构,比传统的遗传算法具有更优良的全局求解能力和计算效率[13]。对种群的主要3个操作:选择、交叉、变异依赖于每个“岛”,将大的种群分成若干个子种群,称之为岛,在各个岛内利用传统遗传算法进行子种群进化。遗传算法配置参数为:每个岛屿个体数目为20,岛屿个数4,种群个体数目为10,迁移率为0.01,迁移间隔为1,交叉概率为0.9,变异概率为0.01。
支撑杆原结构包括4根纵向撑杆和浮筒间的两个横向撑杆,总重大约6 kg。而通过优化计算的新构型,经过801组数据迭代,桁架整体结构质量得出全局最优解,迭代变化如图8所示,所得到的最小质量为5.182 5 kg,与原结构相比质量减少13.6%。在保证材料强度的约束下,优化后各个杆件的具体截面面积如表1所示。
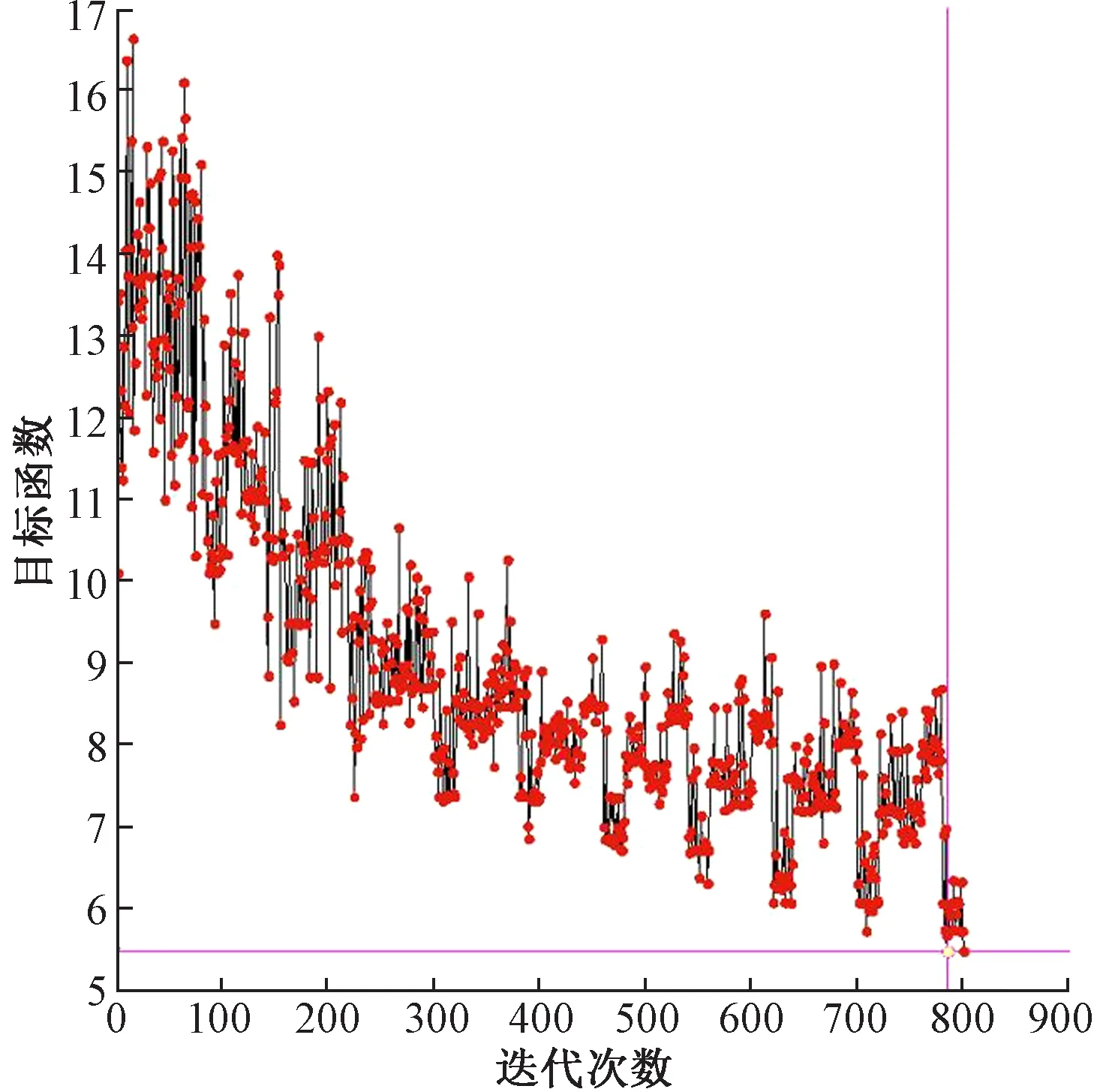
图8 结构质量迭代过程Fig.8 Structural quality iteration process

表1 优化后各杆件的截面面积
3 加装导流罩结构
在实际工程应用中,为了减少浮筒支撑结构对飞机整体气动性能的影响,考虑在杆件外部加装“翼型”整流罩。对于圆柱杆件结构而言,椭圆外形杆件的阻力值和气动噪声比圆柱杆件要小很多[14]。而翼型截面柱体在船舶工程设计中常常被采用,例如尾轴支架,为了降低其产生的附体阻力,多采用翼型或者其他流线型的截面。
这里采用的导流罩分为前缘和后缘两个部分进行设计,前缘形状对于气动减阻方面具有相当大的实用和理论意义。通常对已有恒定半径的圆形前缘进行几何形状的钝化,而幂次外形可以实现所需要的良好钝度。因此前缘采用楔形幂次前缘外形以获得良好的气动外形;后缘采用与圆相切的过渡曲面,将气流平顺地引导至杆件背面,从而实现减阻的效果[15-16],如图9、图10所示。
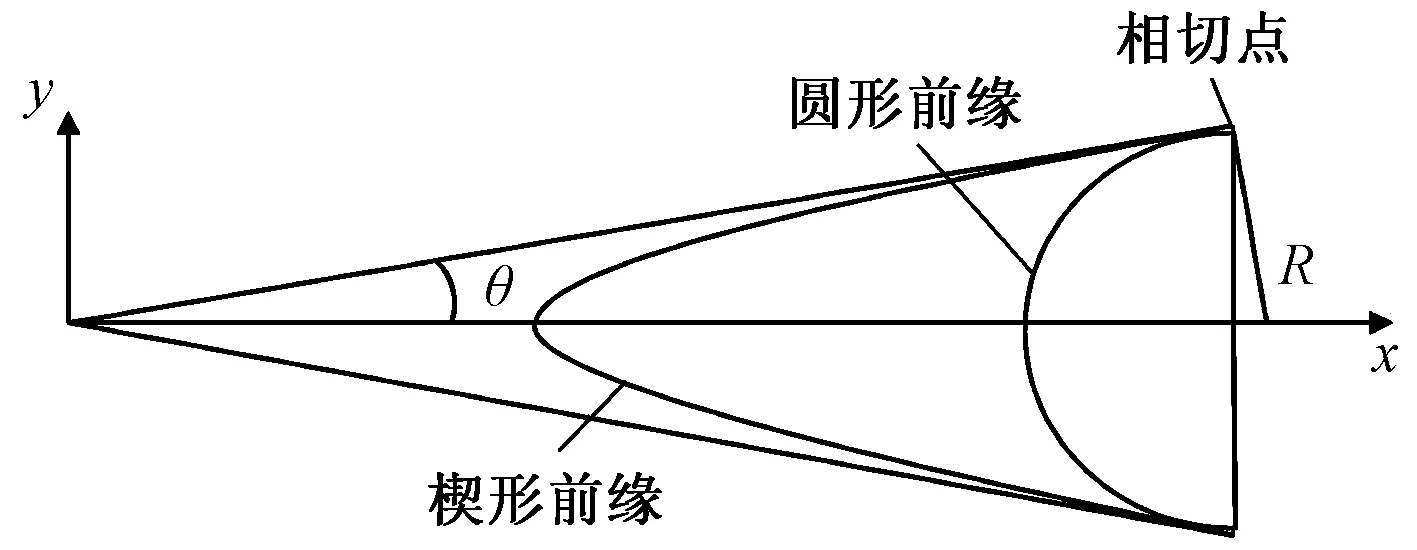
图9 楔形前缘示意图Fig.9 Schematic diagram of the wedge leading edge
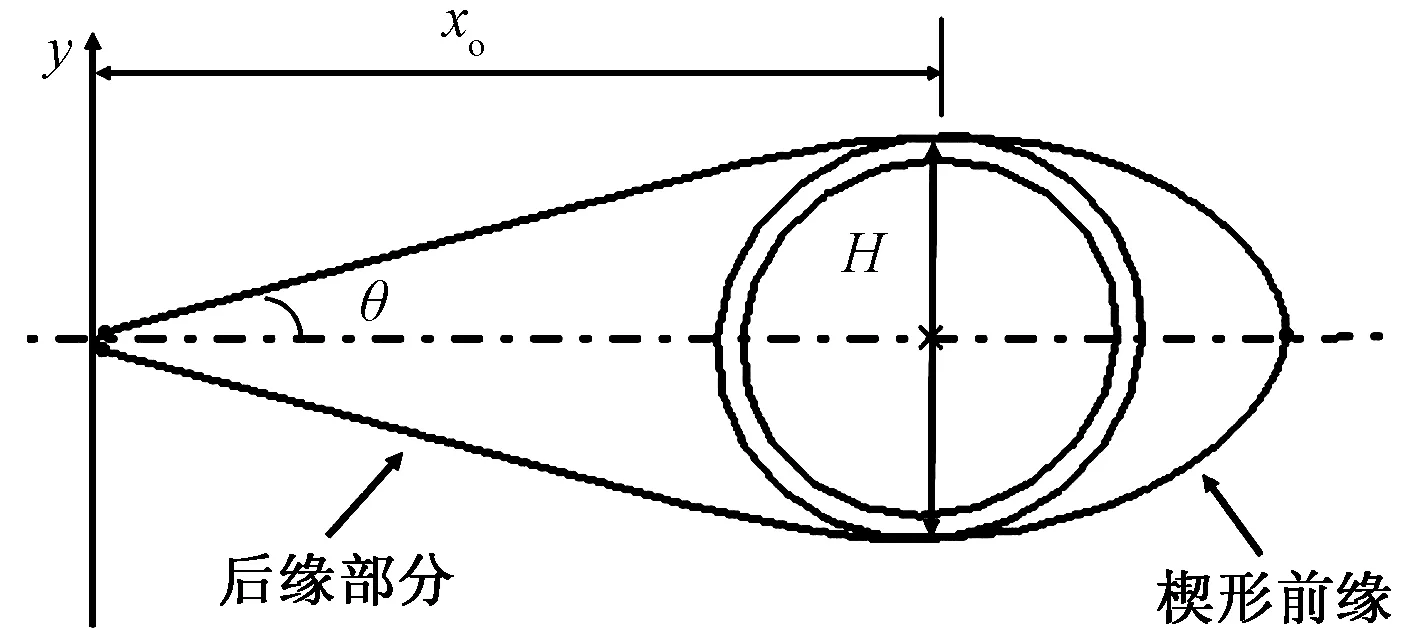
图10 整流罩结构示意图Fig.10 Structure schematic diagram of fairing
3.1 幂次前缘几何定义
二维形式的幂律形状为
y=axn
(25)
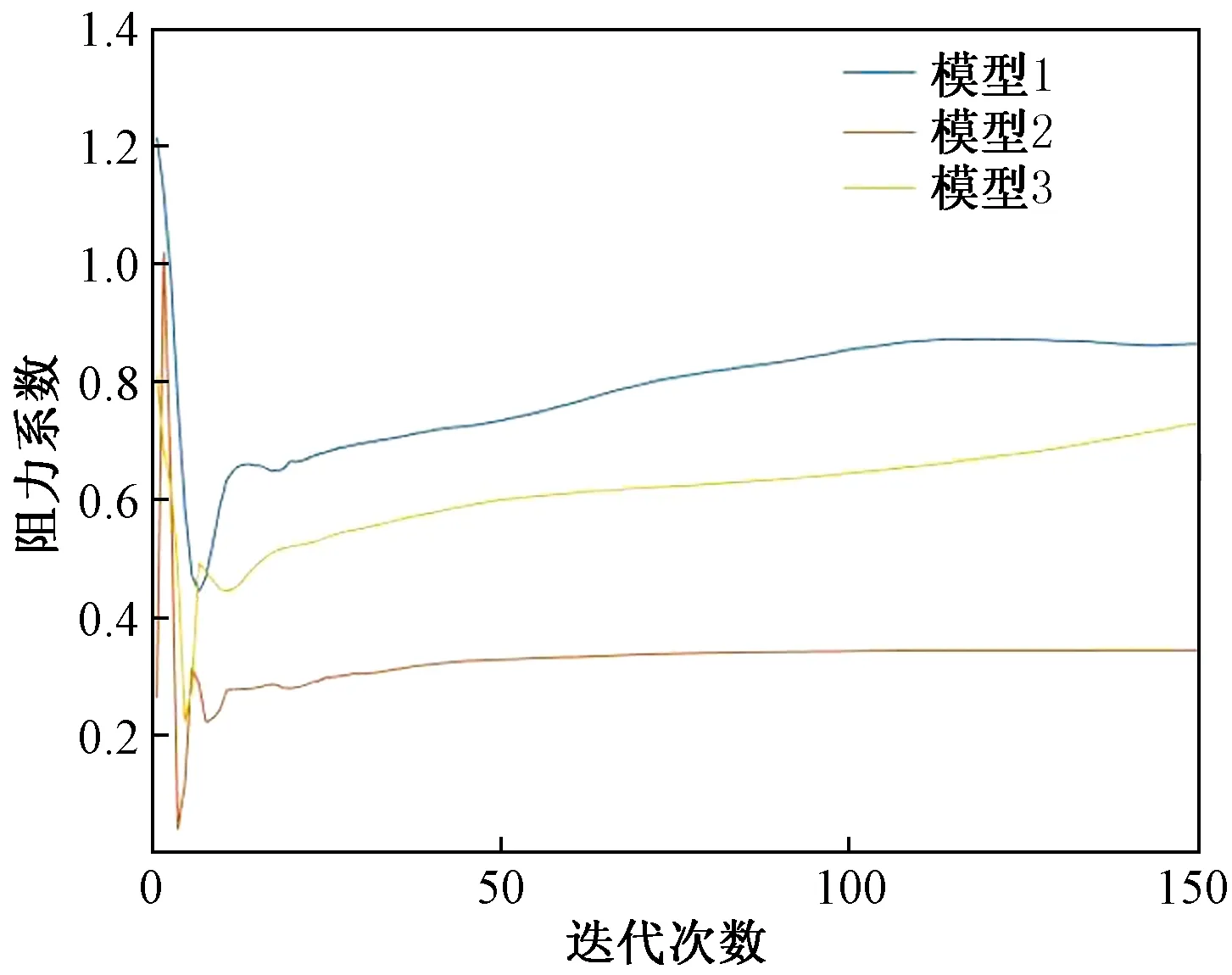
式(25)中:n为幂次外形指数,0 (na)2x4/3(n-2)]3/2 (26) 通过计算和参考实际工程经验,得出了楔形前缘外形参数a和n对气动阻力的影响。常数a取值范围通常为0.17~0.18;阻力系数随着n增大而减小,在0.8~0.9时基本收敛达到最小值。因此这里设定a和n分别为0.175、0.85;后缘半角角度为18°。 首先对原始外形杆件(模型1),增加单一楔形前缘外形杆件(模型2),以及增加完整整流罩杆件(模型3)进行验证分析。为了减小计算量,通过选取支撑杆件的典型尺寸,建立有限元模型,流场模型的入口边界为速度入口,空气流速取飞机最大飞行速度160 km/h,出口设置为压力出口,采用Realizedk-e模型分别对3种不同外形的杆件模型进行流场分布计算。 图11显示了3种模型的阻力系数计算结果,可以看出,加装导流罩的模型1和模型2气动减阻明显,减阻效果为模型3>模型2>模型1,阻力系数降幅分别到达16.4%和60%。 从压力分布云图(图12)可以看出,与原始外形(模型1)相比,杆件前缘弯度减小,前表面压力峰值明显减小,而原始外形在背风侧会产生较大范围的涡流区,产生明显的空气流动分离;在杆件两端出现不稳定的漩涡和气流波动。加装导流罩的杆件(模型3)利用流线型的前缘有效地将气流进行分流,而后缘过渡曲线的存在,减小尾部区域分离涡流的分布与最值,明显降低了迎风与背风区域的压差阻力,显著降低气动阻力。 图11 阻力系数迭代计算图Fig.11 Iterative calculation chart of drag coefficient 图12 杆件压力分布云图Fig.12 Cloud map of bar pressure distribution 利用分级设计优化策略对水上电动飞机浮筒支撑结构进行了再设计,改变了过去依照经验设计的方法。首先利用MATLAB语言所编写的三维拓扑程序获得新的架构方式,然后利用ANSYS和iSight对杆件截面尺寸进行联合优化。新桁架结构在保证支撑强度的条件下,支撑架总质量与原结构相比下降13.6%,最后通过加装“翼型”截面整流罩,减小了杆件前后缘的空气流动分离,减少了阻力,降低了支撑结构对飞机总体气动性能的影响。新结构已应用在B-00EH型水上电动飞机上,整体试飞效果良好,说明了分级优化设计方法的可行性,并为相关工程设计工作提供了一定的借鉴。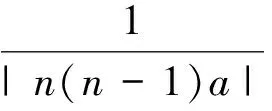
3.2 流场计算
3.3 计算结果分析

4 结论

