辅助墩对大跨斜拉桥在地震作用下的影响
——以禹门口黄河公路大跨斜拉桥为例
梁建军, 巫 炯
(1.中交一公局集团有限公司, 西安 710075; 2.长安大学公路学院, 西安 710064)
近年来,斜拉桥发展迅速[1],因其结构新颖、跨越能力大而成为现代桥梁中最具有竞争力、发展最快的桥型之一[2-3]。对于这种高次超静定柔性结构[4]来说,从静力分析方面,因辅助墩的设置可以提高结构的整体刚度及改善主塔和主梁关键截面的挠度,故大多设计者对该类桥梁采用有辅助墩设计,对于无辅助墩的设计,该类型桥梁受力性能如何,中外也有部分学者进行了这方面受力特性的研究[5]。高金萍[6]指出,就静力分析方面采用无辅助墩方案,斜拉桥的整体刚度将有所降低,而对于有辅助墩的设计,桥梁在主梁跨中的挠度及跨中弯矩、主塔塔根弯矩、塔顶水平位移等内力方面有很大的改善;彭鹏[7]对某双塔双索面PC斜拉桥进行了静力特性方面的分析,结果表明,一个辅助墩的设置对该桥主梁、主塔以及尾索的受力性能和主梁的挠度有很大程度的改善;喻梅[8]分析了辅助墩的数量对主塔个数不同的斜拉桥静力特性的影响,同样得出有辅助墩的设置亦有利于提高多塔斜拉桥整体刚度,且主塔的内力及位移均有所降低的结论。
就辅助墩的设置数量对斜拉桥受力性能的影响来看,大多学者均分析研究了在静力作用下辅助墩数量影响斜拉桥受力特性,而对于跨度较大的斜拉桥进行设计时,动力特性方面的分析是必不可少的。Flieming等[9]对跨度200 m的斜拉桥加入几何非线性问题进行抗震研究;Nazmy[10]建立了基于Wilson-θ法的非线性时程分析方法,经历了反复计算得出主跨大于600 m的斜拉桥几何非线性会有较为明显的影响。之后薛素铎[11]对跨径300~450 m的四座斜拉桥进行动静力作用下的研究,得出大跨径斜拉桥应当考虑几何非线性,其对结构的动静力学响应均有较大的影响。美国对斜拉桥的抗震设计进行了大量的研究,编著了《斜拉桥设计指南》,但其中对于抗震设计的部分过于简略。中国也有大量的专家学者针对大跨度斜拉桥的抗震性能进行研究,并且取得了不少成果,可是目前仍然无统一标准,大跨径斜拉桥在进行抗震性能设计和地震响应分析时考虑的因素众多,对大跨度斜拉桥在抗震设计方面还有很长的路要走。至于辅助墩的设置对抗震性能的影响问题更有待解决。现以禹门口黄河公路大桥作为依托工程,进行地震作用下,从改变结构辅助墩的数量出发,研究其对结构主要截面的内力及线形的影响,得出相应结论,以期为同类型桥梁的设计研究提供参考。
1 工程概况
图1 全桥立面图Fig.1 Full bridge elevation
陕西禹门口黄河大桥主桥为(245+565+245) m 的双塔双索面钢-混组合梁斜拉桥,总长为 1 055 m。斜拉桥主梁横断面的布置形式为双工字型钢梁+混凝土桥面板,桥梁宽度为27 m(不含布索区),主梁断面全宽 30.25 m(含布索区)。纵向为半漂浮体系,索塔采用“H”形,钢筋混凝土结构,设置上、下两道横梁,塔柱分为上、中、下3部分。该桥立面图如图1所示。
2 有限元模型的建立
运用CSiBridge有限元分析软件建立不同辅助墩位置的有限元模型,经过多次对比分析最终分别确定了一个和两个辅助墩方案的合理位置:一个辅助墩模型的最终辅助墩位置建立在距过渡墩0.3倍的边跨跨径处,两个辅助墩模型最终将两个辅助墩分别建立在0.25及0.5倍的边跨跨径处,无辅助墩模型即为原设计方案。上述不同辅助墩方案的全桥模型如图2所示。
3 动力特性分析
对桥梁结构的自振周期、振型等动力特性进行分析对于抗震研究来说具有十分重要的意义。对该大跨组合梁斜拉桥分别进行了无辅助墩、一个辅助墩和两个辅助墩模型的自振特性分析计算,得到3种模型的前10阶自振频率f和振型,并给出了其自振频率的对比图,如表1和图3所示。
通过表1及图3可知辅助墩对斜拉桥动力性能的影响有如下特点。
(1)在上述3种方案中,随着模态的增加每种方案的频率都相应增加,由图3可以直观地看出,频率随模态的增加而增加的显著趋势只有在前4阶模态中比较突出,从第4阶开始,随着阶数的增加频率逐渐增加的这种变化趋势逐渐减小,特别是到了第6阶模态以后,几乎没有什么变化。就辅助墩个数的改变对自振频率的影响来看,增加辅助墩的设置使该大跨组合梁斜拉桥各阶模态所对应的频率相应增加,但就一个辅助墩和两个辅助墩的设置来看,这种变化趋势并不明显。由此可得:增设辅助墩会增大该大跨组合梁斜拉桥的整体刚度,但增设两个辅助墩对刚度的提高并不显著。
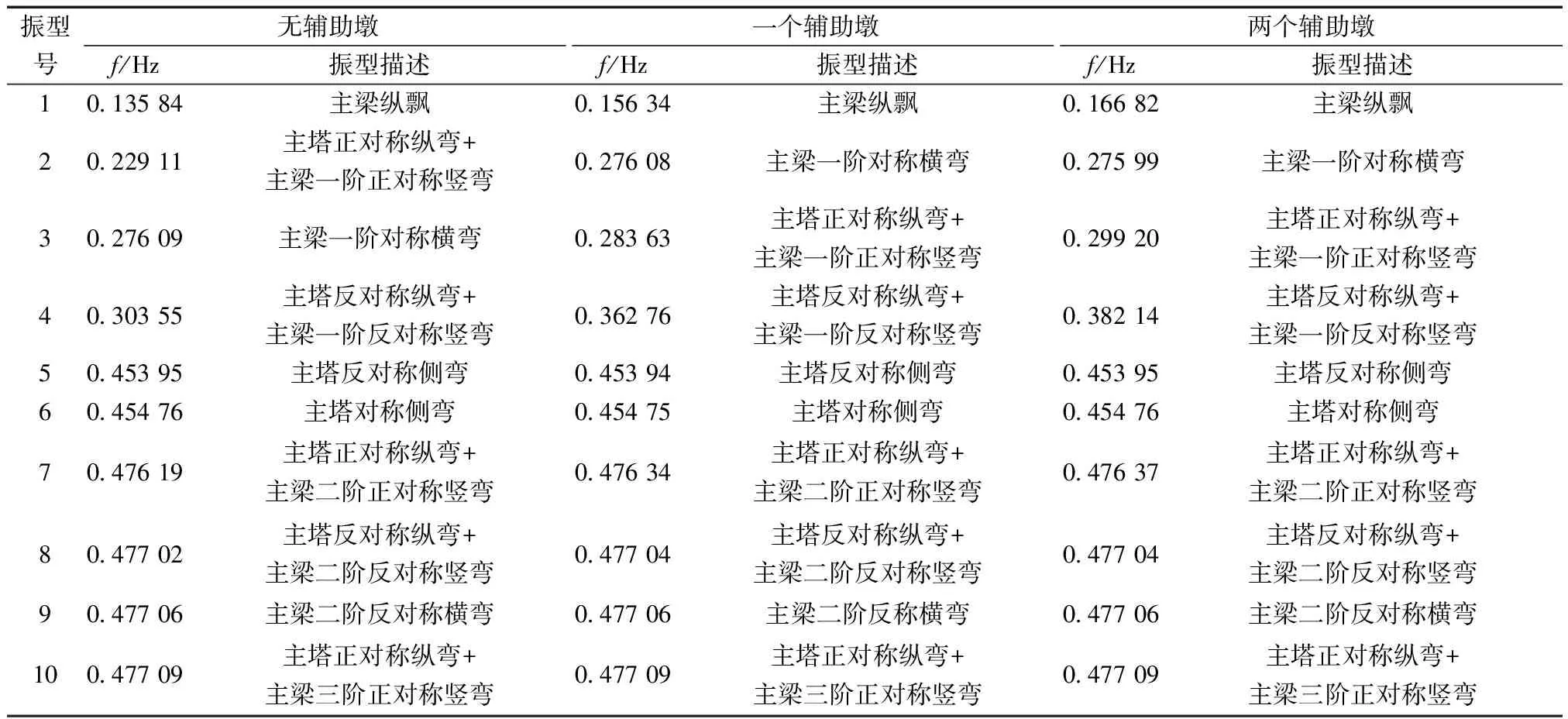
表1 3种模型前10阶自振频率及振型特点

图2 斜拉桥全桥模型Fig.2 Full bridge model of cable-stayed bridge

图3 各个方案下自振频率对比Fig.3 Comparison of natural vibration frequency under each scheme
(2)在上述3种方案中,无论何种辅助墩方案的一阶模态均为主梁纵飘,且此时的自振频率相对于后面几阶振型来看均为最小,由此可以看出该种振型在本组合梁斜拉桥的纵向地震响应中具有十分重要的地位。通过对一个辅助墩和两个辅助墩方案与无辅助墩方案相比较,可以得出一个辅助墩的设置方案其一阶模态的频率增加了13%,两个辅助墩的设置方案其一阶模态的频率增加了18%,两个辅助墩的设置比一个辅助墩频率增加了6%,这说明该结构增加辅助墩的设置对其纵向刚度有影响,但就设置一个辅助墩及两个辅助墩的方案来看,对纵向刚度影响不大。
(3)在上述3种方案中,从第3阶模态(不包括第3阶)之后3种方案的振型一致,自振频率的变化也越来越小。可以看出无辅助墩的第3阶模态与有辅助墩的第2阶模态一致,就振动频率来看,一个辅助墩方案与两个辅助墩方案均比无辅助墩方案的振动频率增加了约17%,即增加辅助墩的设置可以提高该大跨组合梁斜拉桥结构的竖向刚度,对结构抵抗竖向变形能力有利。
(4)在上述3种方案中,由各种方案的2、3阶振型可以看出,当主梁出现1阶对称横弯模态时,3种方案的结构频率基本一致。由此看出,辅助墩的设置对该大跨组合梁斜拉桥的横向弯曲几乎没有影响。
(5)综上所述,增设辅助墩对该斜拉桥的整体刚度、纵向刚度以及竖向刚度均有所提升,而对横向刚度的影响并不明显。
4 地震响应分析
4.1 地震波的输入
反应谱法是当前结构抗震设计中广泛使用的方法[12],根据禹门口黄河公路大桥的抗震设计要求,水平向设计加速度反应谱按文献[13]确定,选取主梁和主塔的关键截面分别进行该斜拉桥在E1、E2水准的横向+竖向、纵向+竖向共4种工况的上述3种方案下关键截面内力及线形对比。
地震作用下的动态时程分析,在选取地震波方面主要从以下几个因素考虑:峰值、频谱特征、持时和数量,综合考虑上述影响地震波选取的因素,最终从PEER地震动数据库中选取3条符合该桥梁场地特征的地震波进行3种辅助墩方案的时程对比分析,选取的3条地震波分别为ChiChi地震波、Imperial Valley地震波和Loma Prieta地震波。采用横向+竖向和纵向+竖向的地震激励方式,其中竖向时程取值为水平时程的1/2。主要工作内容如图4所示。用x、y、z分别表示横向、顺向、竖向。
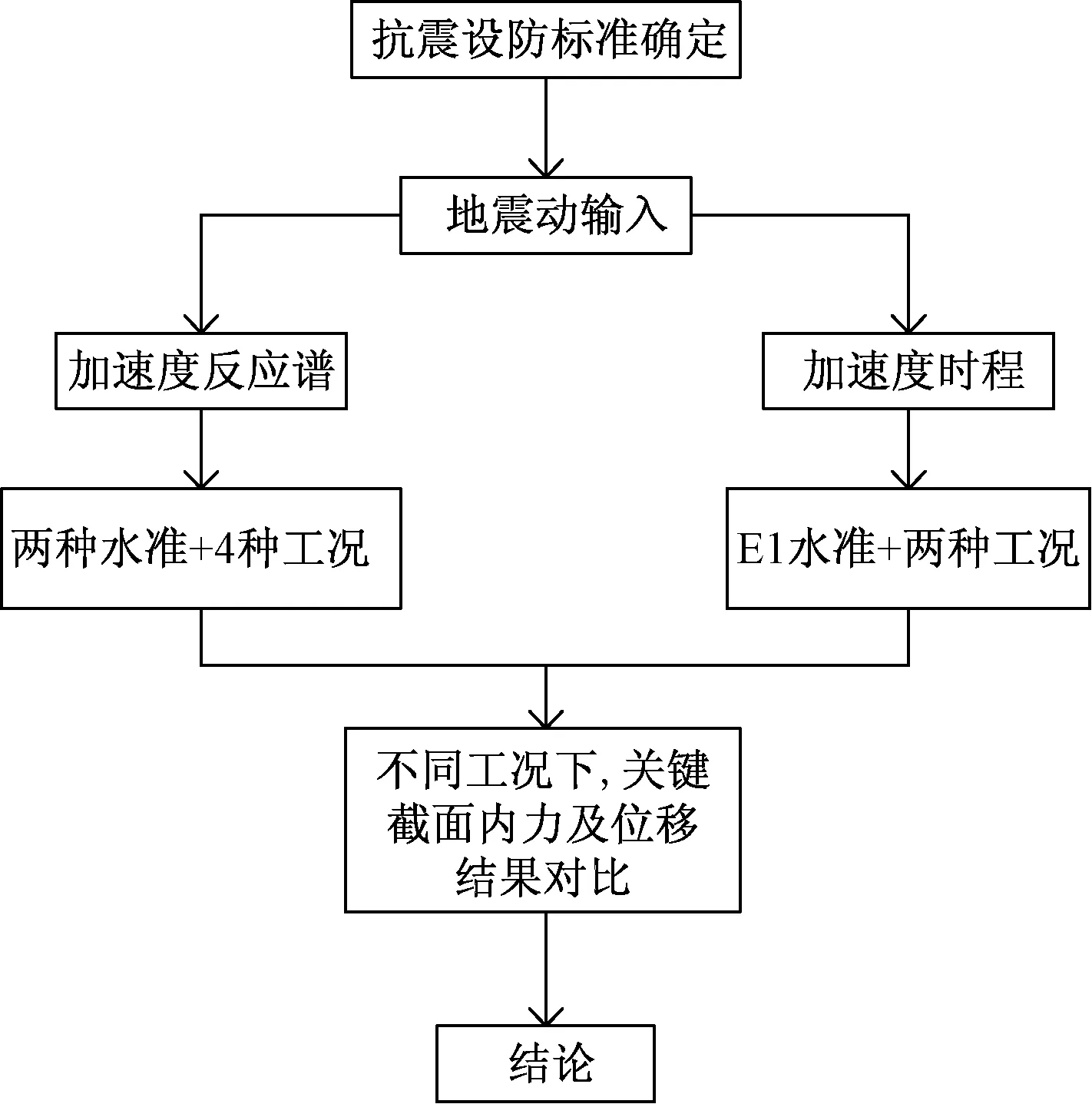
图4 主要工作内容流程Fig.4 Flow chart of main work content
4.2 结果对比分析
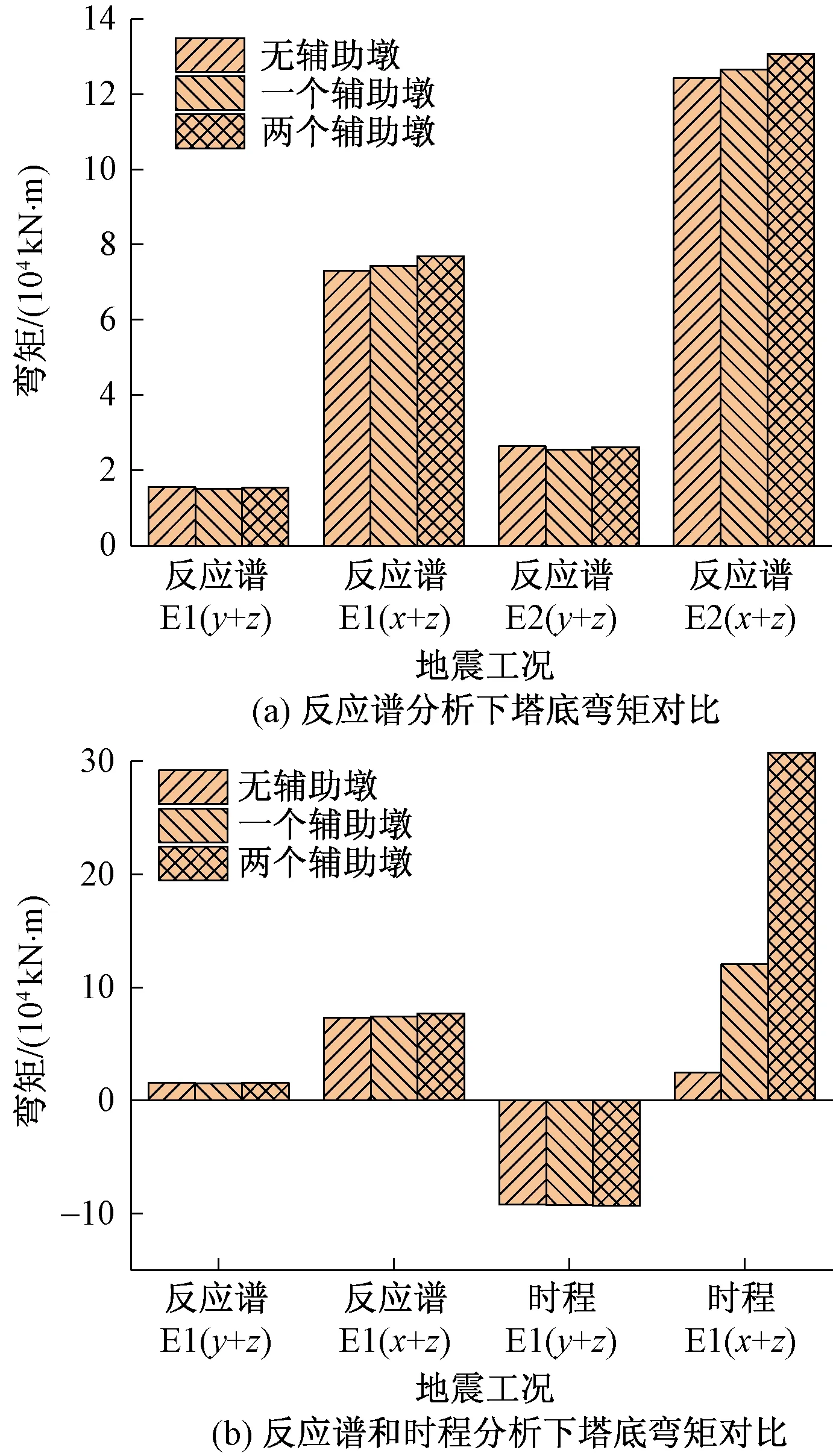
图5 塔底弯矩对比Fig.5 Comparison of bending moments at the bottom of tower
如图5所示,无论对于横向+竖向(x+z)还是纵向+竖向(y+z)地震力作用,在反应谱分析下的E1和E2两种水准来看,该斜拉桥塔底的弯矩变化值具有基本一致的变化趋势;3种辅助墩方案下,横向+竖向工况的塔底弯矩值总远大于纵向+竖向的塔底弯矩值,这表明:对主桥桥塔塔底而言,受到横向+竖向地震力作用时,其受力性能更为不利;无论是E1还是E2水准,在纵向+竖向工况下,均为一个辅助墩方案下塔底弯矩相对较小,无辅助墩和两个辅助墩方案塔底弯矩均有所增加但增加值并不显著;而对于横向+竖向工况,3种方案均为采用无辅助墩时塔底弯矩较另两种方案小。再由反应谱和时程的对比分析来看,二者分析结果差异较大,纵向+竖向地震工况时,塔底弯矩出现正负之分,且3种方案下时程分析的负弯矩值明显大于反应谱分析,而对于横向+竖向工况,由时程分析来看,增加辅助墩的设置塔底弯矩增加明显,而反应谱分析相差甚微。
如图6所示,就反应谱分析而言,当纵向+竖向地震力作用时,无论在E1水准还是E2水准下,无辅助墩方案的边跨跨中弯矩值都是最小的,而一个辅助墩与两个辅助墩方案的弯矩值都有所增加,其增加值相对于无辅助墩方案来说分别为62%和31%;在横向+竖向地震力作用下,在E1、E2两种水准下均为两个辅助墩方案下的主梁边跨跨中弯矩值最小,而无辅助墩方案的弯矩增加值相对于两个辅助墩方案来说为22%,而无辅助墩方案的弯矩增加值相对于两个辅助墩方案来说为42%。就反应谱分析和时程分析的结果对比来看,在纵向+竖向地震力作用下,时程分析下的无辅助墩方案弯矩值明显减小,一个辅助墩方案为负弯矩,两个辅助墩方案弯矩增加明显,在横向+竖向地震力作用下的无辅助墩方案亦为负弯矩,其余两种方案表现出了与前者类似的规律,且随辅助墩数量的增加,边跨跨中弯矩值增加明显。
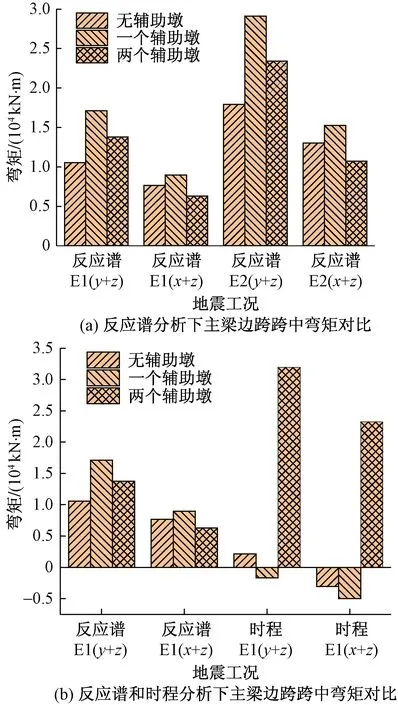
图6 主梁边跨跨中弯矩对比Fig.6 Comparison of bending moments of the middle span in the side span of the main beam
如图7所示,对于主梁中跨跨中弯矩值而言,3种方案下的反应谱分析无太大差别,两个水准变化趋势相近,且弯矩值E2水准大于E1水准。就反应谱分析和时程分析的对比来看,后者在E1水准 3种方案两种工况下,弯矩值均大于前者,且随辅助墩数量的增加负弯矩值也明显增加。
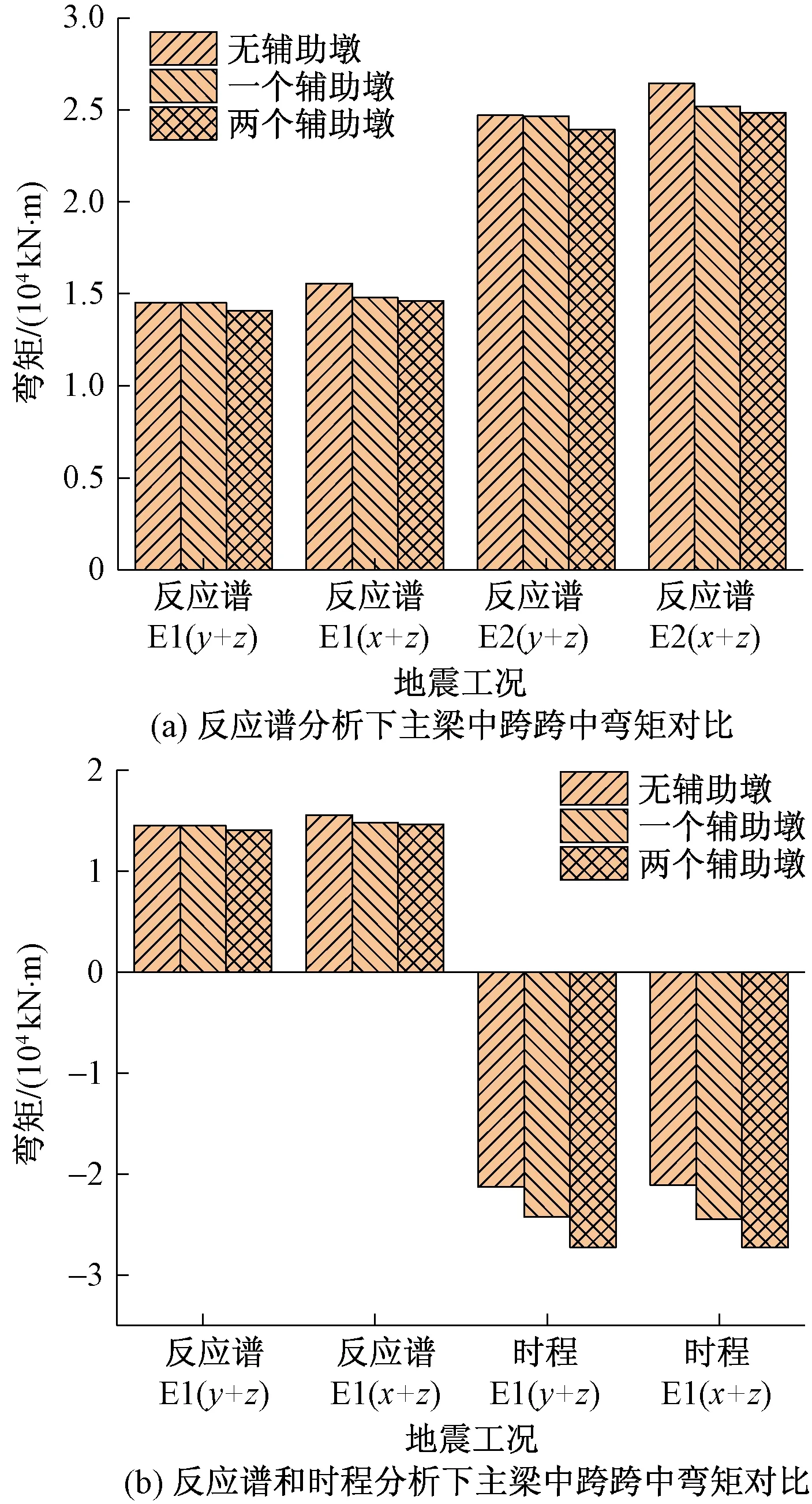
图7 主梁中跨跨中弯矩对比Fig.7 Comparison of bending moments in the span of the main beam
由图8可以看出,反应谱分析下,无论是E1还是E2水准,在纵向+竖向地震力作用下全桥的纵向位移量基本相同,中跨跨中的位移值相对有所增加但并不显著。在E1水准下,就反应谱分析和时程分析对比来看,3种方案的纵向位移值随主梁坐标的增加而减小,且变化趋势基本相同,在两种分析方法下均为无辅助墩方案的纵向位移量最大,且随辅助墩数量的逐渐增加主梁的纵向位移值均依次减小。由此可看出,增加辅助墩的设置能明显限制主梁的纵向位移量。
由图9可以看出,在反应谱分析下,对于边跨跨中,两种水准下均是两个辅助墩方案的竖向位移最小,一个辅助墩方案的竖向位移值最大,这可能与辅助墩对主梁的支撑作用有关;对于中跨跨中,两种水准下均为两个辅助墩方案下位移值有所增加,一个辅助墩方案的主梁竖向位移值最小。但无论是位移值的增加还是减小,这种变化趋势均不显著。就反应谱分析和时程分析对比来看,时程分析下主梁中跨跨中竖向位移值增加较大,边跨跨中反而有所减小,但 3种方案下的变化趋势基本相同,均为中跨跨中无辅助墩时最小,边跨跨中两个辅助墩时最小。可以看出,在横向+竖向地震力作用下,就全桥的竖向位移来说,辅助墩仅对边跨有利,而对中跨来说相对不利。
5 结论
就已有辅助墩对大跨径斜拉桥在地震作用下的响应影响研究来看,大多学者均单从反应谱分析或时程分析出发,总结规律得出结论,这样的研究并不全面。分别进行了这两方面的研究并对两种分析方法进行了对比,得出以下结论。
(1)单从反应谱分析来看,增加辅助墩的设置对提到的3方面弯矩的影响不大,甚至是不利影响;而对于纵向位移有明显的减小,竖向位移针对主梁不同截面影响有利有弊。
(2)单从时程分析来看,增加辅助墩的设置对提到的3方面弯矩的影响较大,均为不利影响;而对于纵向位移有明显的减小,竖向位移针对主梁不同截面影响有利有弊。
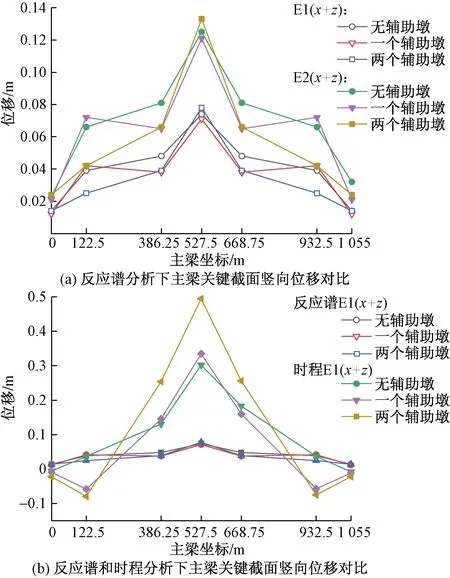
图9 主梁关键截面竖向位移对比Fig.9 Comparison of vertical displacement of key section of main beam
(3)从反应谱分析和时程分析的对比来看,二者结果出入较大,但对于主梁中跨跨中弯矩、纵向和竖向位移来说,二者在3种辅助墩方案下总体变化趋势一致。

