磁浮列车悬浮系统的反步控制方法及实验研究

张文跃， 佟来生， 朱跃欧， 徐俊起， 荣立军

(1.中车株洲电力机车有限公司磁浮系统研究所, 株洲 412001； 2.同济大学(国家)磁浮交通工程技术研究中心, 上海 201804)

磁浮车辆作为新型轨道交通工具,具有无摩擦,低噪音,转弯半径小,爬坡能力强等优点。中外已有多条磁浮交通线路投入运行,未来这种新型交通工具有望得到大力发展和应用[1-3]。但由于磁浮车辆的悬浮系统是一种复杂的非线性系统,具有开环不稳定,易受扰,耦合性强等特点,传统的线性控制方法(proportional-integral-derivative, PID),已经难以满足运载速度不断提高对悬浮控制精度和鲁棒性的要求[4]。

悬浮系统是磁浮车辆的核心和关键部件之一。近些年来在现代智能控制技术的推动下,中外学者对高性能磁悬浮自动控制进行了大量的研究,取得了一定进展。刘德生等[5]利用中间变量将原非线性系统以线性形式表达,但本质仍然是非线性系统,进而利用丰富的线性理论对控制器进行设计。吕志国等[6]基于反馈线性化和在线参数辨识提出一种自适应控制方法,能够实现小球的稳定悬浮。Zhou等[7]针对electro magnetic suspension(EMS)型磁浮列车悬浮系统设计了带有FIR(finite impulse response)滤波器的自适应控制方法来减小车辆的振动。孙友刚等[8]将可变边界层和指数趋近律结合,设计一种改进型的滑模控制方法,仿真和实验证明该方法可以提高系统鲁棒性。张静等[9]针对磁悬浮系统提出了无源控制器,仿真结果表明该方法能提高磁悬浮系统抗干扰性能。Sun等[10]基于模糊控制理论设计了自适应控制器。该方法能够自动调整控制参数以使闭环系统远离Hopf分叉点,避免车轨耦合振动的发生。Xu等[11]提出了一种基于磁通密度反馈的自适应滑模控制器,该方法可以提高系统的稳定裕度。这些现代智能控制方法推动了磁悬浮控制系统的发展,但是仍然存在一些问题。如反馈线性化控制抗干扰能力较差；模糊控制无需建立精确的数学模型,但是控制稳态精度较低。无源控制一般只能借助注入阻尼来设计控制律,稳定性难以保证。反步(Backstepping)法可将复杂的非线性系统分解成不超过系统阶数的子系统,然后为每个子系统分别设计Lyapunov函数和中间虚拟控制量,通过设计和修正虚拟控制律确保非线性系统的稳定性,可实现磁浮车辆系统的悬浮控制。该方法具有稳定性分析无须线性化或近似,控制性能优良的优点。

首先搭建了磁浮车辆悬浮系统动力学模型,然后基于反步法设计了新型悬浮控制器,借助 Lyapunov 函数最终获得悬浮系统实际的控制律,然后基于 Lyapunov稳定性理论严格证明了控制系统的稳定性。 最后通过仿真和实验证明所提控制方法的有效性。

1 磁浮车辆悬浮系统动力学建模

悬浮系统是磁悬浮列车的核心部件之一,结构如图1所示。电磁铁模块沿磁浮列车的左侧和右侧两边排列。磁浮列车的悬浮架具有结构解耦功能[12],每个单点悬浮控制系统可以认为在一定范围内彼此独立。因此,研究单点悬浮系统的控制性能具有通用性,可以将单点悬浮系统视为控制器设计的最小动力学单元[13]。

Nm为电磁铁线圈匝数；xm(t)为悬浮间隙;Am为电磁铁的磁极面积；Fm[im(t),xm(t)]表示电磁吸力；um(t)和im(t)分别表示电磁铁线圈的电压和电流；m为名义悬浮质量；fd(t)为扰动力；g为重力加速度图1 磁浮列车悬浮系统示意图Fig.1 Schematic diagram of suspension system of maglev train

根据麦克斯韦方程和毕奥-萨伐尔定理,悬浮电磁铁和轨道间的电磁吸力为

(1)

式(1)中：Wm[im(t),xm(t)]为磁场能量,可表示为

(2)

由电磁学的基尔霍夫定律可得

ψm[im(t),xm(t)]=Nmφm[im(t),xm(t)]=

(3)

式(3)中:ψm[im(t),xm(t)]表示间隙磁链；φm为总磁通量；R(xm)为磁阻,可表示为

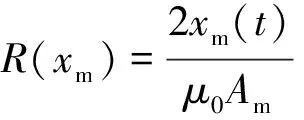
(4)

式(4)中：μ0为真空磁导率。依据式(1)～式(4)可将悬浮电磁铁和轨道间的电磁吸力改写为

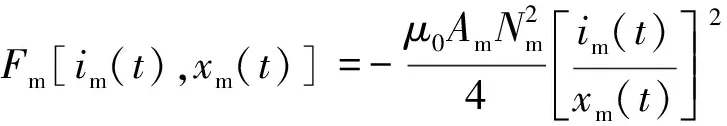
(5)

电磁铁线圈的电压可以表示为

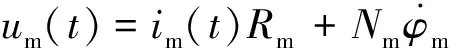
(6)

(7)

式(7)中：Lm为电感,可描述为

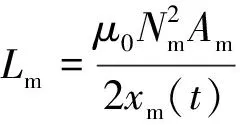
(8)

由式(6)～式(8)做简单数学变化,整理后有

(9)

将式(9)代入式(6)得

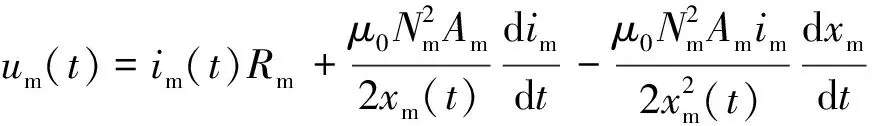
(10)

式(10)可以重新写为

(11)

根据牛顿第二定律,得到系统垂向运动方程为

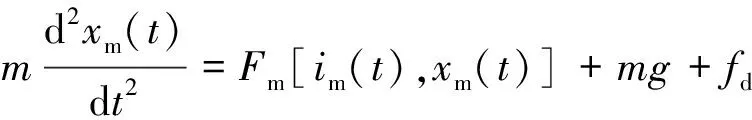
(12)

将式(5)代入式(12)有

(13)

综上所述,常规单点磁浮系统的数学模型可表示为

(14)

显然,式(14)表现出强非线性,对控制器的设计提出了很大的挑战。

2 控制器设计

图1所示的磁浮列车悬浮系统的动力学方程可由式(14)完全确定。目前悬浮控制系统采用串级控制的结构,将悬浮系统分为电流环和位置环两个子系统[14]。电流环可由斩波器实现,而针对位置环进行控制器的设计,此时为电流控制器u=im(t)。

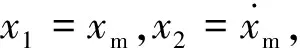
e1=x1-xd

(15)

(16)

选取一级子系统的Lyapunov候选函数为

(17)

第一级子系统的虚拟控制量定义为u1,则

(18)

式(18)中：e2(t)为辅助信号误差，其表达式为

e2(t)=-u1(t)+x2(t)

(19)

根据式(15)～式(19),设计u1为

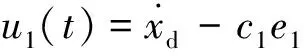
(20)

式(20)中：c1为控制系数,且c1>0。

将式(20)代入式(18)可得

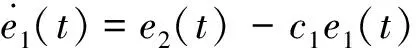
(21)

对式(17)两边求导可得

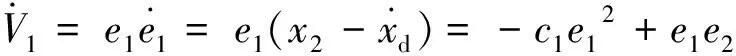
(22)

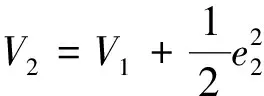
(23)

式(23)中：V2为二级子系统的Lyapunov候选函数；V1为一级子系统的Lyapunov候选函数；e2为辅助信号误差。

对式(23)两边求导,并代入式(14)可得

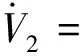
(24)

根据Backstepping法和(24),设计非线性的悬浮控制器为

(25)

式(25)中：c2为控制器系数,且c2>0。

为了证明Backstepping控制器的稳定性,将式(25)代入式(24)可得

(26)

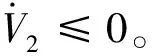
3 仿真分析

磁浮列车悬浮系统的参数取值如表1所示。

表1 悬浮系统的参数

对于Backstepping控制器,c1=40,c2=20。为了证明所提控制器的优越性,将所提控制器的仿真结果和线性PD控制器的仿真结果进行对比。

PD控制器的设计过程为:首先,利用泰勒公式在平衡点位置附近求得系统线性状态。

令

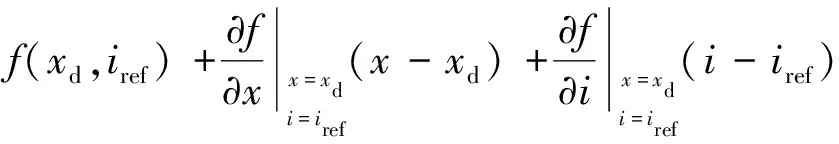
通过简单的计算,最终可得平衡点附近的悬浮系统的线性化方程为

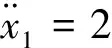
(27)

设计线性PD控制器为

(28)

式(28)中：upd为PD控制器,kp为比例系数,kd为微分系数。

根据式(27)和根轨迹法[4],可以选取PD控制器的参数为kp=4 500,kd=1 500。

通过MATLAB/Simulink搭建磁浮列车仿真模型,并分别采用线性PID控制器与Backstepping控制器,气隙响应的仿真结果如图2所示。

从图2可以看出，Backstepping法没有传统线性PD控制器中超调的现象,且所提控制方法的静态误差基本为零,而PD控制器静态误差为0.91 mm。超调和静态误差容易导致磁浮列车有效悬浮间隙变小,容易引发车辆撞击轨道,威胁磁浮列车运行安全。

图2 悬浮气隙响应比较的仿真结果Fig.2 Comparison of response of suspension air gap of simulation results

磁浮列车在运行中不可避免地会遭受外部干扰的影响。为了验证本文方法在干扰下的鲁棒性,在仿真中引入如图3所示的外部非线性干扰力。仿真结果如图4所示。

图3 外部干扰力Fig.3 External disturbance force

图4 干扰下悬浮气隙响应的仿真结果Fig.4 Response of air gap with disturbance of simulation results

由图4可以看出,悬浮系统在外部干扰下存在0.31 mm的气隙波动,但仍然能稳定悬浮。这说明所提出的Backstepping具有很强的鲁棒性。

4 实验结果

通过单点磁悬浮实验平台来进一步验证所提出的控制策略的有效性。因为在全尺寸的磁浮列车上做实验比较困难,搭建了如图5所示的单电磁铁悬浮系统。由电磁铁、车厢载荷(添加钢板改变质量),二系弹簧和dSPACE 实时控制系统组成。相关控制算法都可以在MATLAB/Simulink中编程实现对单点悬浮试验台实时控制。

图5 单点磁悬浮实验平台Fig.5 Single point maglev experimental platform

实验将单点悬浮模块从初始位置悬浮到目标位置。其气隙动态响应如图6、图7所示。

由图6、图7可知,所提出的Backstepping控制方法能够实现系统稳定悬浮,且没有超调和静态误差,进一步证明了该方法的有效性。

图6 气隙动态响应Fig.6 Dynamic response of air gap

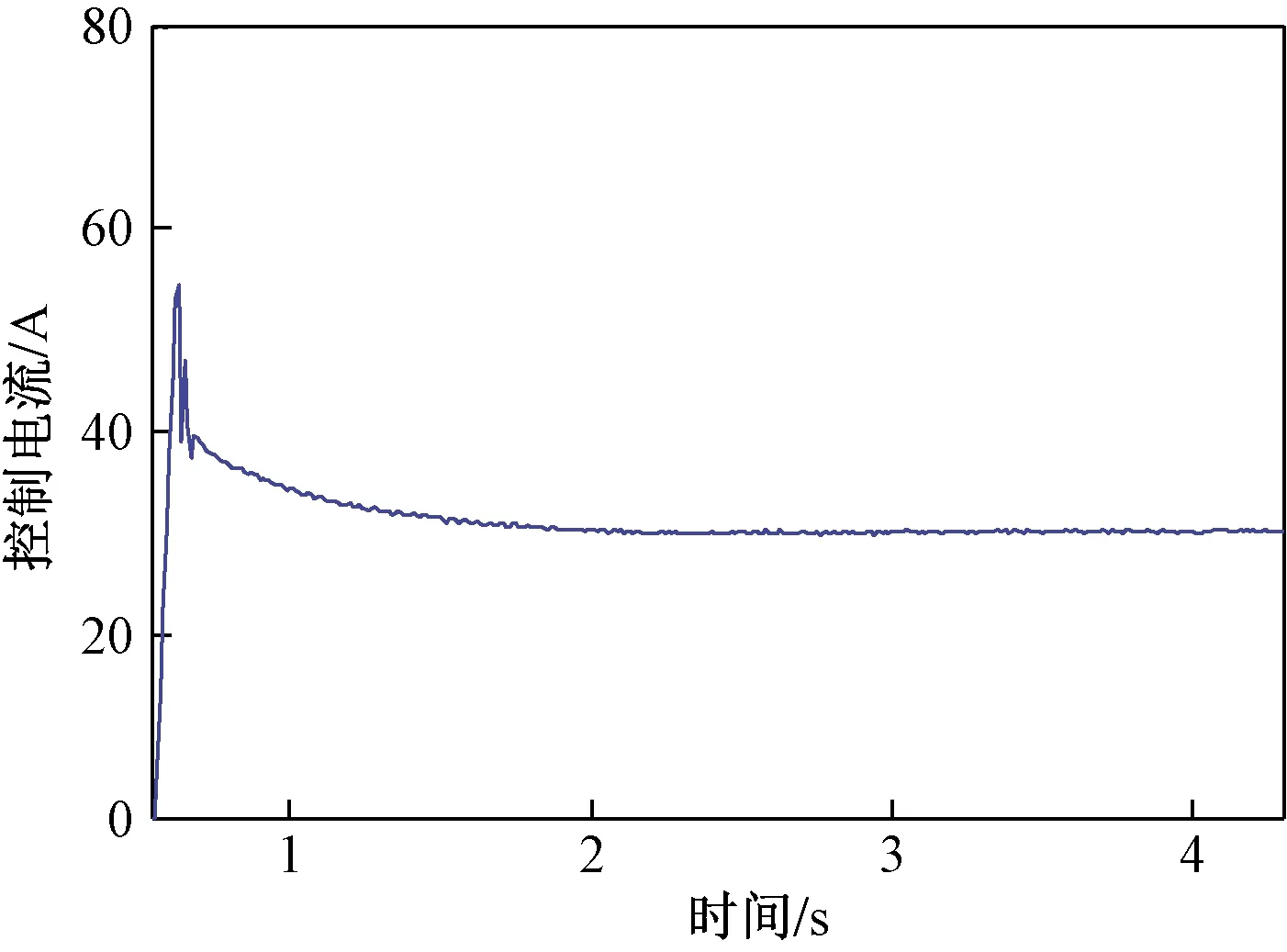
图7 控制电流响应Fig.7 Control current response

5 结论

针对磁浮列车的单点悬浮系统的悬浮控制,提出了Backstepping控制方法。选取磁浮列车的单点悬浮系统为最小动力学单元,建立了系统的动力学模型,并在MATLAB/Simulink中搭建悬浮控制系统,进行仿真研究。将Backstepping控制器和线性PD控制器进行比较,结果表明Backstepping控制方法具有更好的动态表现,且没有稳态误差。当存在外界干扰时,也能很好的抑制干扰对悬浮系统的影响,鲁棒性较强。最后,实验结果表明该控制方法具有很快的响应速度和很高的悬浮精度。因此该控制方法有效,符合磁浮列车悬浮系统设计的要求。