蓄热体与换热时间的数值模拟分析
邵和平, 汪建新*, 张庆宇, 吴启明, 王佳微
(1.内蒙古科技大学机械工程学院, 包头 014010; 2.北京京诚凤凰工业炉工程技术有限公司, 北京 100176)
高温空气燃烧技术因具有环保、节能、效率高等特性[1],受到广泛的关注。该技术在运用中表现出提高能源使用效率、有害气体排放极少等优势[2-3]。蓄热体[4]是蓄热室内反应过程中的转换媒介,有助于烟气中热量的回收和对空气的预热,也是高温空气燃烧技术不可缺少的重要部分[5-6]。
高温空气燃烧技术发展以蓄热式热交换技术为基础的集环保、节能于一身的燃烧技术,也称蓄热式燃烧技术[7-8]。近年来,蓄热室的结构设计对蓄热体的换热特性和能量交换效率的提升起着关键作用,研究人员针对这方面开展了多次研究。郑志伟等[9]运针对蜂窝状蓄热体而研究发现,蓄热体在热交换过程中压力会随着气体流动速度和蓄热体的长度改变而改变。表现为蓄热体越长,气体温度越高,热量回收效果越高。王皆腾等[10]通过从蓄热室换热效率及温度散失研究,表明了不同规格和尺寸的蓄热体有着不一样的最佳换向时间,蓄热体长度越长则最佳换向时间将延长。杜玮等[11]通过对蓄热体的传热和阻力等特性上实验得到,蓄热体的阻力损失随着体积流量的扩大而增加,且在入口温度一定时,换热效率会随着比表面积的扩大而提升。吕情恒等[12]通过对球体蓄热体的热饱和时间进行分析求解得出,对流系数适当的增加会减少蓄热体的热饱和时间,而蓄热体的直径和选材会使得其呈线性递增。Li等[13]、贾力等[14]在蜂窝状蓄热体上通过对冷周期和热周期稳态时刻的分析,能获取蓄热体在时间上的流动阻力特性。
目前,前人对于蓄热体的研究工作探讨的因素主要集中在蓄热体热量传递和流动特性[15]。然而对于蓄热体自身在内部的位置随时间而变化的温度分布及热饱和时间的研究尚鲜见报道。为此,将采用数值模拟方法对蓄热期、冷却期进出口温度和壁面的温度进行探讨,对于计算特定的蓄热体材料的热饱和时间及由该材料构成的蓄热式燃烧系统的换向时间具有一定的指导意义。
1 数值计算
针对蓄热式换热器研究的技术路线是:①找到热交换的平衡方程;②进行方程常规的离散化;③得到差分方程并讨论其敛散性;④利用对应的已知条件解得所需答案。
1.1 假设条件
蓄热体吸放热量的途径有三种不同的组合—产生的烟气进行放热或预热的空气需要吸热;蓄热体蓄热和产生的烟气热交换;蓄热体内部的导热、蓄热和放热。简化计算,做如下假设:①组成蓄热体的任意小球其特性一样,对任一球体进行单位化进行探讨,并且小球与外壁是隔开而不传热的;②不考虑蓄热室中通过其他形式传热;③介于两个连续的冷却周期,在即将结束时刻,在排烟口处温度与上一周期相差3 ℃以内,表明此时处于热交换的稳定阶段。
1.2 蓄热体的选择
选择陶瓷小球,如果为正方排列堆叠,如图1(a)所示,材料层的孔隙率是最大的,并且如果是自由堆积的形式;如果为自由堆积,如图1(b)所示,材料层的孔隙率是最小的。在一般工程,在已知的孔隙率两者范围内,并不是由球直径大小而改变的,可以将蓄热室内部所用材料看作其透气性是均匀分布的,以便于对模型中采用正方排列方式进行数值模拟。
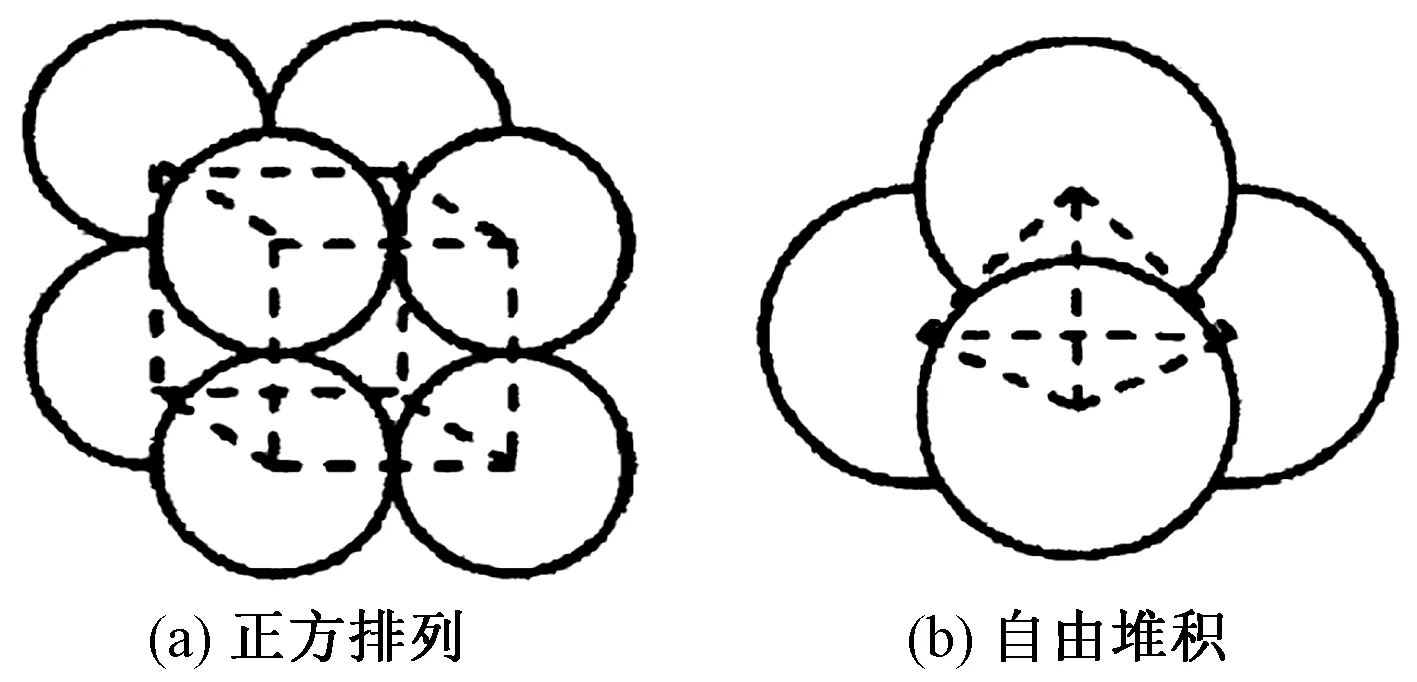
图1 排列方式Fig.1 Arrangement mode
1.3 物理模型的建立
蓄热体直径为12 mm,蓄热室模型如图2所示,蓄热室为100 mm×100 mm×100 mm的立方体方体,壁厚10 mm,蓄热体物理参数如下:密度3 000 kg/m3,比热容为1.05 J/(kg·℃),导热系数为1.1 W/(m2·℃)。

图2 蓄热室模型Fig.2 Regenerator model
1.4 数学模型
陶瓷小球组成的蓄热体热量之间的传递能够用如下方程表达。
(1)连续性方程:
(1)
(2)动量方程:
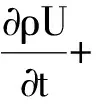
(2)
式(2)中:t为时间,s;P为压强,Pa;μ为动力黏度,N/m2·s;SM为控制方程的源项。
(3)能量方程:

(3)
式(3)中:htot为换热系数,W/(m2·℃);λ为气体导热系数,W/(m2·℃);T为气体与固体温差,℃;SE为控制方程的源项。
(4)理想气体状态方程:
P=ρRT
(4)
式中:R为气体常数,J/(mol·℃);T为体系温度,℃。
(5)固体内部导热方程:

(5)
式(5)中:ρs为固体密度,kg/m3;cp,s为固体定压比热,J/(kg·℃);λs为蓄热体热导率,W/(m2·℃);Ts为固体温度,℃。
(6)边界条件:
Tg|x=0=Tg1,Ta|x=L=Ta1,
vg|x=0=vg1,va|x=L=va1
(6)
式(6)中:Tg为烟气入口温度,℃;Tg1为初始的速度场为零时的烟气入口温度,℃;Ta为空气入口温度,℃;Ta1为初始的速度场为零时的空气入口温度,℃;vg为烟气入口速度,m/s;vg1为初始的速度场为零时的烟气入口速度,m/s;va为空气入口速度,m/s;va1为初始的速度场为零时的空气入口速度,m/s;L为蓄热体高度,m。
(7)初始条件:
Ts|x=0=T0=26 ℃,u=v=w=0
(7)
式(7)中:T0为环境温度,℃;u,v,w为速度分量,m/s。
(8)换向条件:
Ths|t=t′=Tcs|t=0,Tcs|t=t′=Ths|t=0
(8)
式(8)中:Ths为加热期达到换向时间的温度;Tcs为冷却期达到换向时间的温度;t′换向时间,s。
1.5 计算求解
由于进行计算的区域是由比较规则而组成的立方体形状,需要分解成不均匀的网格。为此涉及壁边界层效应,对离壁接近的区域内划分的网格要求是紧密的。蓄热室内部的蓄热体在反应过程中与气体之间的热量交换:在高温烟气流动下,蓄热体蓄热;进入的冷空气经过蓄热体回收存储的余热后释放被预热至比较高,蓄热体与气体之间进行热量的交替是一个循环的状态,趋于饱和温度的标志是存储热量的介质与室内气体达到一种稳态现象。
给出初始条件入口速度和温度等,分别为:烟气入口温度Tg1=1 200 ℃,流速Vg1=1.69 m/s;出口对外压力P′=0,空气入口温度Ta1=26 ℃,流速va1=0.45 m/s,最初速度场u=v=w=0,蓄热体最初温度Ts0=26 ℃,蓄热室内部最初压力场Pre1=0,其时间长度单位为1 s,得到的结果恰好为一个时间步长。
利用熟悉的离散气体能量方程,可以求出回路中气体温度的分布情况。热量传递方程在气与固体两者中能够得到固体在内部区域的温度变化情况,运用此结果看成初始场。在接下来的运算过程中,能够清晰地看出蓄热体内气体每一时间步长的结果。
2 分析与讨论
为了得到结果的合理性,得到的结论与之现有常用的高温燃烧系统,如表1所示。两端出口的偏差分别是11%、3%以内,因此利用数值解出的答案是有依据的。

表1 计算数值与实测值对比
2.1 蓄热体的温度分布
在最起始的几个循环过程中,蓄热体和内部的烟气之间温度差还是有很大区别,因此容易出现较大对流换热,并且存储的热量较大,与此同时作为中间介质与冷流体之间的温度差却很小,也不难看出在其间比没有很强烈的对流作用,所以放出的热量较小。当这个过程趋于稳定时,会出现存储的热量减少,而释放的热量却在增加的现象,最后到二者分别趋于一种平衡状态。启动过程中,图3、图4为蓄热期蓄热室进口、出口温度分布;图5、图6分别为蓄热小球、壁面温度云图;图7、图8分别为冷却期蓄热室进口和出口温度分布;图9、图10分别为蓄热小球、壁面温度云图。

图3 蓄热期蓄热室进口温度云图Fig.3 Inlet temperature cloud diagram of regenerator during heat storage period

图4 蓄热期蓄热室出口温度云图Fig.4 Temperature cloud diagram of regenerator outlet during heat storage period

图5 蓄热期蓄热体温度云图Fig.5 Temperature cloud diagram of heat storage body during heat storage period
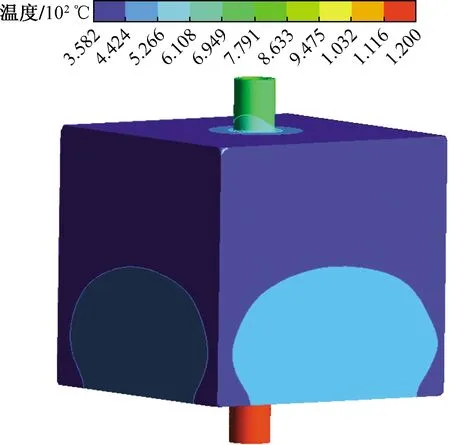
图6 蓄热期蓄热室壁面温度云图Fig.6 Temperature cloud map of regenerator wall during heat storage period
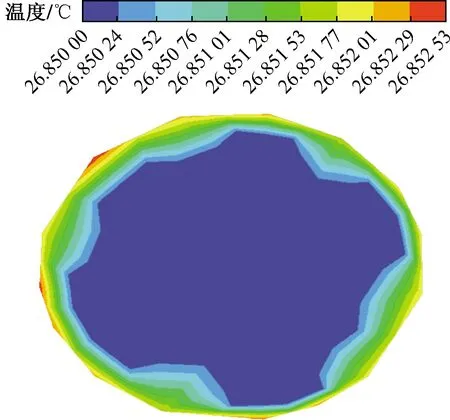
图7 冷却期蓄热室进口温度云图Fig.7 Convey diagram of inlet temperature of regenerator during cooling period
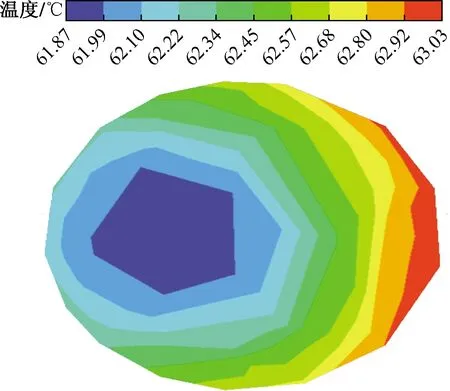
图8 冷却期蓄热室出口温度云图Fig.8 Temperature cloud diagram of regenerator outlet during cooling period

图9 冷却期蓄热体温度云图Fig.9 Temperature cloud diagram of heat storage body during cooling period

图10 冷却期蓄热室壁面温度云图Fig.10 Temperature cloud map of regenerator wall during cooling period
2.2 运行之中的蓄热室内温度分布解析
由图11(a)可知,在出口处显示出烟气的温度情况是由起初好几次的快速上升,接着幅度开始减小,结束时接近于水平状态。
由图11(b)可知,换向次数的增加会直接影响到出口空气的温度,并且换向次数越多温度就会越高。

图11 反应过程中烟气、空气出口温度随时间变化趋势Fig.11 Trend of flue gas, air outlet temperature change with time during the reaction process
2.3 稳定状态时蓄热室内部温度分布分析
如图12所示,在最初阶段,蓄热室内的蓄热体未经吸热且温度不是很高,经过对高温度的烟气吸收热量,蓄热体温度开始慢慢升高,随后出口处的烟气温度慢慢下降。不难看出在冷却时期,此时组成蓄热体的小球温度比较高,因此蓄热体与空气接触很全面且反应剧烈,换热率达到不错的预期。所以推出空气在进行预热时候,温度还是很高的,由于时间在慢慢地推移,由于换热导致蓄热体温度越来越低,换热的效率也会随着温度降低而降低,最后在出口处检测到地空气温度也会慢慢变低。
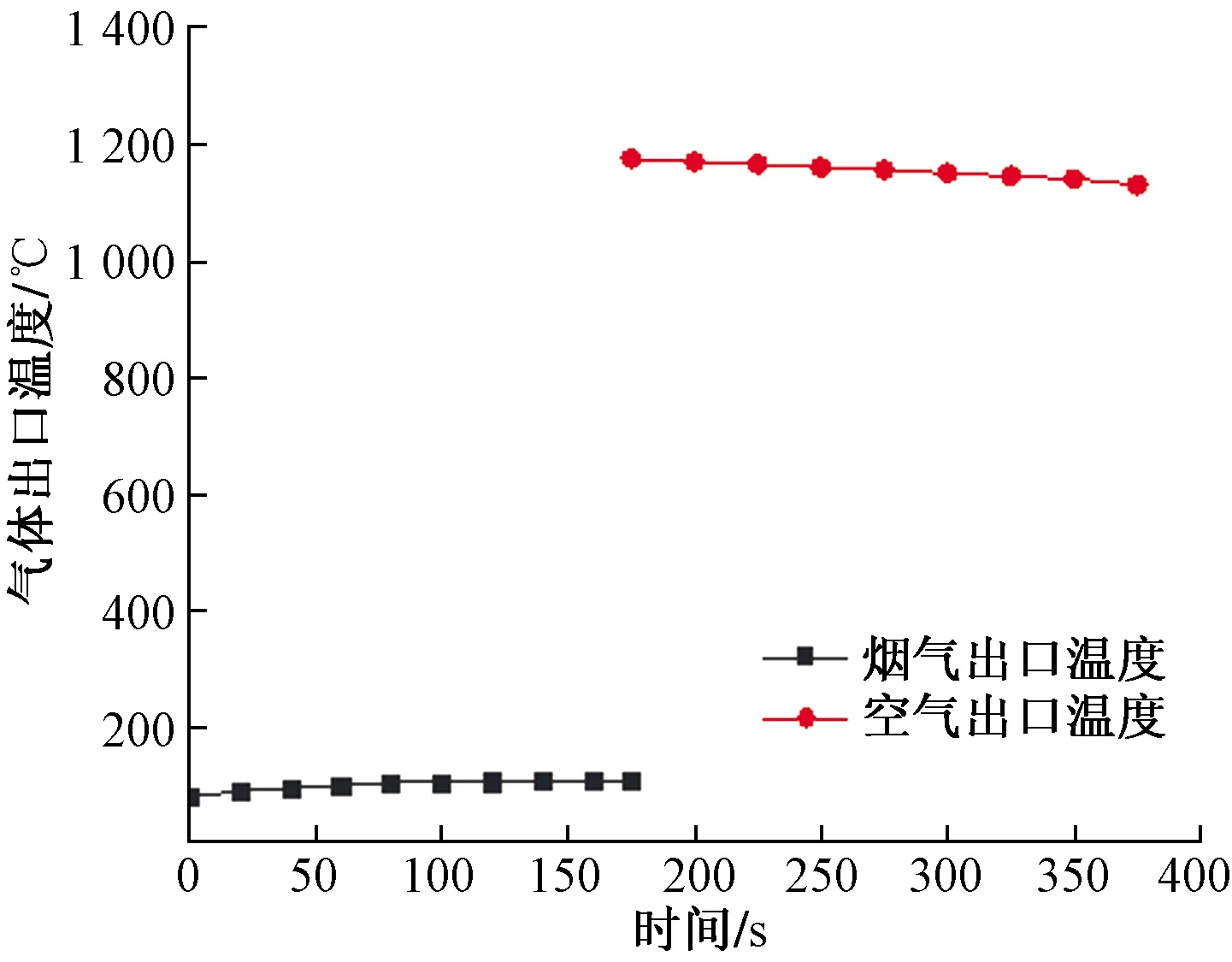
图12 一个换向周期中的出口烟气与空气温度变化趋势Fig.12 The trend chart of outlet flue gas and air temperature in a commutation cycle
3 结论
通过模拟实验得出如下结论。
(1)运行过程中,在蓄热阶段,蓄热体(蓄热小球)能够较好地吸收高温度的烟气带来的热量,经过一段时间,蓄热体(蓄热小球)并不能有效转换烟气中含有的热量,而达到饱和状态,烟气残余的热量较多,通过出口排出的温度慢慢上升。
(2)蓄热体内的温度和气体出口都是随着换向次数的增加才上升的,若换热进行到稳态时,蓄热体表现为热、冷周期的时,对应着温度升高和下降差值是相等的,此时出口温度达到一个稳定状态。在稳定状态时刻中的某一周期内,蓄热体和蓄热室内温度在时间上呈线性变化。
(3)在蓄热过程中由于蓄热体(蓄热小球)能够有效吸收热量大于放出预热空气的热量,直到两者相同,整个运行处于稳定工作状态。
(4)从蓄热体的横截面温度分布分析,在整个蓄热体内4个面上中间处换热效率高,在4个角落换热效率较差,还有在蓄热体的温度在横截面上分布还是比较均匀的。

