压裂裂缝间距优化设计
张矿生, 唐梅荣, 陈文斌, 徐创朝, 杨典森, 周再乐*
(1.中国石油长庆油田油气工艺研究院, 西安 710021; 2.中国科学院武汉岩土力学研究所, 武汉 430071)
水力压裂已经成为非常规油气资源开采的必要手段,其中多裂缝间距的设置已经成为缝网压裂优化和设计的关键问题。对于压裂过程中多裂缝的延伸问题,中外的许多学者都做了大量的研究。
刘翔鹗等[1]在中国较早开展了二维和三维水力压裂物理模拟试验,分析了压裂所形成的裂缝特点、裂缝形态随地应力的变化关系。刘建中等[2-3]对水力压裂室内模拟认为,裂缝扩展是一个非连续的过程,井筒水平段取向的改变可以使裂缝呈现出I-II型复合裂缝的特点,在形态上表现为S型。陈勉等[4]周健等[5]组建了大尺度(30 cm×30 cm×30 cm)的水力压裂试验系统,为多裂缝的水力压裂试验创造了条件。Zhou等[6]通过多簇射孔的压裂试验发现,相对于常规连续泵注而言,循环泵注可以起裂更多的射孔簇;而采用更高的压裂液黏度可以增强这种效果。无论在常规连续泵注和循环泵注条件下,更高的泵注压力有助于起裂更多的水力裂缝。侯冰等[7]通过开展真三轴水力压裂试验建立了水力裂缝网络扩展规模评价方法。
夏海帮[8]采用新型的压差聚合胶结型暂堵剂用于页岩气压裂优化暂堵,从而形成了更为复杂裂缝网络。刘威[9]结合不同泵注参数对支撑剂在缝内的铺置进行模拟,影响改造效果的排量、液量、砂量以及前置液比例等关键参数进行优化,实现体积改造最优化。蒋廷学等[10]基于常压页岩气井改造中的难题,从射孔方式、人工裂缝控制及支撑技术、现场施工工艺及压裂材料等多方面进行优化,研究探索了配套的高密度缝网压裂工艺方案,初步实现了多簇裂缝均衡延展及多尺度人工裂缝网络。王飞等[11]提出了宽带体积压裂技术理念,即通过在原人工裂缝侧向开启次生裂缝或沟通天然裂缝,增加裂缝带宽,对宽带体积压裂裂缝的合理带宽进行了优化,建立了合理裂缝带宽计算方法,在此基础上采用正交试验方法对主次裂缝的导流能力,裂缝半长等其他缝网参数进行了优化设计。张勇等[12]针对高应力差地层,提出采用提高缝内净压力的方法来促使天然裂缝发生剪切破坏,从而形成更为复杂的网络。
通过对水力裂缝在含缺陷、弱面以及呈各向异性地层扩展过程的研究,Daneshy[13]发现随着裂隙张开度的增加,裂隙对水力裂缝的延伸偏移作用也会增强;随着裂隙长度的增加,裂隙对水力裂缝偏转作用也会显著增强。Blanton[14]研究发现,水力裂缝的延伸受到已有水力裂缝的影响。随着现有水力裂缝长度增加和缝内流体压力的升高,后起裂的水力裂缝偏向已有的水力裂缝的趋势逐渐增强,甚至发生相交。
Cleary[15]在考虑岩石各向异性的情况下,认为现有裂缝或者裂隙能够吸引或者排斥临近正在延伸的水力裂缝。Thallak等[16]通过有限元方法模拟了两条裂缝的相互作用,发现两裂缝前缘之间会相互排斥,临近裂缝所产生的“应力阴影”的作用甚至要大于远场地应力作用。Jeffrey等[17]通过数值模拟研究了多裂缝延伸问题,发现保持两条平行裂缝同时延伸所需的净压力比单条裂缝情况下要高,裂缝间相互争夺缝宽,每条裂缝缝宽均比单条裂缝时的缝宽要窄。Palmer等[18]认为,对于多条平行延伸的裂缝而言,缝内净压力值与裂缝条数平方根成正比。Warpinski等[19]对多级压裂进行研究,发现前一级压裂所形成水力裂缝会对后一级压裂时水力裂缝的起裂及延伸产生影响,尤其是当裂缝间距较小时,这种影响会更加显著。为了减小“应力阴影”所造成的影响,Fisher等[20]建议平行裂缝的间距应该大于1.5倍的裂缝缝高。
Ben-Naceur等[21]推导出了多产层水力裂缝同时延伸模型。Elbel等[22]通过对多裂缝剖面的分析,给出了各个产层进液量分配的定量计算方法;相对于限流压裂前期根据射孔眼数个数来简单分配液量的方法,该方法在准确性和数学理论严密性方面均有大幅度的提高,Olson[23]也提出了多裂缝延伸流量分配的近似解析。Gu等[24]将拟三维模型与流量的动态分配相结合提出了自己的多裂缝延伸模型。该模型能够考虑裂缝砂堵或者射孔孔眼磨蚀后对流量分配以及裂缝延伸速度的影响。
而在储层中的岩石非均质性较强以及应力分布存在很大的不确定性,上述数值计算研究中往往通过DDM(边界元)以及FEM(有限元)往往假定地层为理想的均质地层,且需要通过冗长复杂的数值迭代才能对裂缝间距来进行优化,而在地层性质难以了解透彻的情况,结果与实际仍然偏差较大。因此前面文献中所采用的裂缝间距优化方法计算复杂,在操作的便捷性方面难以满足现场的压裂的施工设计。故而现场施工设计更需要一种简单易行的方式来对裂缝间距进行优化。
无论在国外还是国内,开采非常规油气资源最为常用的方式就是水平井多裂缝分段压裂技术。在储层中多条裂缝间的相互干扰即“应力影”效应,又促使形成更为复杂网状裂缝,达到了体积压裂的效果。对于页岩超低渗致密储层而言,体积压裂相对于常规压裂而言具有更大的泄流面积,故而能够取得更好的储层改造效果。
在压裂施工过程中,每一条裂缝的张开都会挤压其周围的地层,所形成的力称之为诱导应力。而多条裂缝间诱导应力的相互叠加又会影响各条裂缝本身的延伸,即形成 “应力影”效应[25-26]。现从单裂缝诱导应力场基础分析出发,根据诱导应力场能够降低页岩储层水平地应力差(σH-σh)的特点[27-29],提出了较为实用的有裂缝间距间距设计方法。
1 水力裂缝引起的诱导应力模型
水平井多级压裂过程中最为常用的是分簇射孔压裂技术,即用桥塞将水平井段分为若干压裂段,每一段包含2~5个射孔簇。在压裂过程中,裂缝会从各个射孔簇处起裂并延伸,如图1所示。
为了对裂缝间距(簇间距)进行优化,这里从基础的诱导力学解析解出发进行分析。

图1 水平井多级压裂示意图Fig.1 Diagram of multi-stage fracturing in a horizontal well
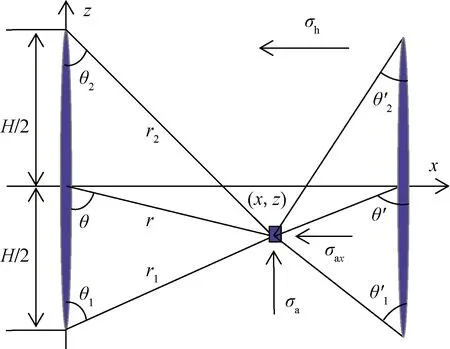
假设无限大储层内有一条竖直面内水平延伸的双翼形裂缝,以垂直裂缝面的方向为x轴,缝长方向为y轴,缝高方向为z轴,当裂缝缝长相对于缝宽尺寸足够大时,该裂缝附近地层的形变计算可视为平面应变问题。如图 2 所示,垂向应力σv沿着z轴方向,水平最小主应力σh沿着x轴方向,水平最大主应力σH沿着y轴方向。则此时二维垂直裂缝在点(x,z)的诱导应力场分量[27-28]为

(1)

此时水平最大和水平最小主应力方向的综合应力可用公式表示为
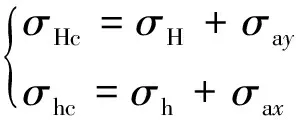
(2)

图2 单条裂缝下的诱导应力计算示意图Fig.2 Calculation diagram of induced stress under single hydraulic fracture
2 水力裂缝诱导应力场及缝间距优化
2.1 诱导应力的基本变化特征
以中国某区块页岩储层为例,其地层参数如下:最小主应力σh=40 MPa,最大主应力σH=42 MPa,σv=62 MPa,压裂后裂缝内流体压力p=45 MPa,泊松比μ=0.22,以裂缝缝高H=60 m为例,水力裂缝所产生的诱导应力在水平最大和最小主应力方向的值及二者的差值随距离坐标x的变化曲线如图3所示。

图3 水平主应力方向的诱导应力随距离坐标x的变化曲线Fig.3 Variation curve of induced stress vs distance coordinate x along the horizontal principal stress
由图3可知,最小主应力σh方向的诱导应力值σax大于最大主应力σH方向的诱导应力σay,由式(1)可知,水力裂缝本身的出现会显著减小裂缝周围水平最大和最小主应力的差。
2.2 低应力差储层的簇间距优化
致密储层压裂施工作业中,水力裂缝附近诱导应力在原最小主应力σh方向的分量要高于最大主应力σH方向的应力分量[30-31],当原有致密储层的最大地应力σH和最小地应力σh相差不大时,并满足方程时,裂缝附近区域诱导应力的产生往往会使原最小主应力方向的综合应力值σhc超过原最大水平主应力方向的综合应力值σHc,即产生应力反转现象,通过求解不等式可以将应力反转区域求出。
σH-σh<(σax-σay)max
(3)
即
σH+σay≤σh+σax
(4)
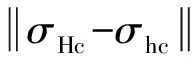
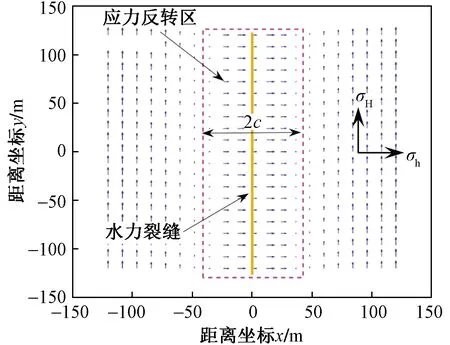
图4 应力反转区域示意图Fig.4 Schematic diagram of stress reversal area
在x轴上θ1=θ2,θ=π,应力反转边界与裂缝之间的距离c,可通过方程求出σHc=σhc,即

(5)
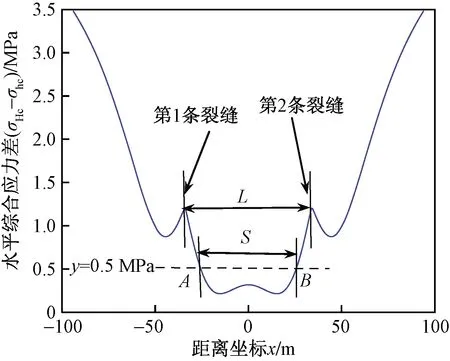
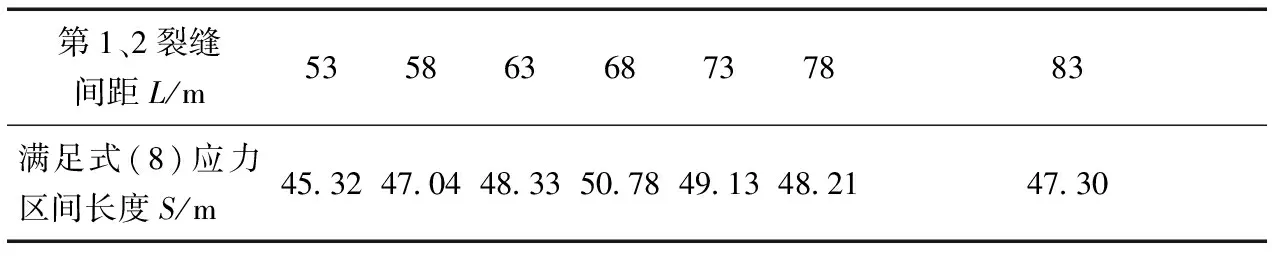
应力反转区域可表示为-c 在对致密储层进行大排量水力压裂过程中,在应力反转区域以内,压裂液会在现有裂缝的垂直壁面方向(即新的最大主应力方向)上起裂形成新的正交T形垂直裂缝。当有足够多的该T形裂缝产生时,即可相互连通形成网状裂缝,故而在水平地应力相近的储层,即使采用较大的裂缝间距往往也能取得很好的开发效果。 在这种情况下,此时为了使射孔簇压裂能够形成复杂缝网,所需采用的簇间距值的最优值Dopt应为 Dopt=2c (6) 当前大量的研究表明[30-36],在对致密储层进行多级压裂过程中,当水平最大和最小主应力的相差越大,射孔簇起裂时越容易形成长而宽的双翼形缝,储层改造效果往往较差。而当地层两水平主应力相差越小时,水力压裂越容易形成复杂裂缝。 而当水平地应力差条件无法满足不等式时,这里可以采用近距离布置若干水力裂缝,利用多条水力裂缝诱导应力的相互协同叠加作用,促使原场水平地应力的差异性进一步减小。此时调整裂缝间距将地层的综合水平应力差值(σHc-σhc)降低到一定范围时,通过在双裂缝中间插入新射孔簇,起裂时即可形成复杂分枝状裂缝。通过优化裂缝附近的应力差(σHc-σhc)的方式来反过来优化裂缝间距,即射孔簇的间距,其计算示意图如图5所示。 图5 多裂缝下的诱导应力的叠加计算示意图Fig.5 Calculation diagram of induced stress superposition of multiple fractures 对于每一特定力学性质的储层来说,都存在一临界地应力门限差值K,在该应力差值范围内,压裂时能够很好地形成网状裂缝,临界门限应力差值K与储层脆性、应力状态和压裂施工条件密切相关,可通过岩石三轴压裂物模试验得出[6,37-40]。只有当该井段区域水平地应力差值差小于K时才能在水力作用下形成有效的网状裂缝。此时令综合应力差函数为 φ(L)=(σH+σay1+σay2)-(σh+σax1+σax2) (7) 式(7)中:σay1、σax1为第1条裂缝沿最大、最小水平主应力方向产生的诱导应力;σay2、σax2为第2条裂缝沿最大、最小水平主应力方向产生诱导应力。 若存在一连续区间x∈[x1,x2],使得该区间内任意x值都能满足 0≤φ(L,x)≤K (8) 由于远场地应力差(σH-σh)本身较大,即使在叠加诱导应力作用下也难以到达复合应力差φ(L)=0的状态,此时令 (9) 则此时满足方程中综合应力差条件的井段长度S为 S=x2-x1 (10) 当第1条和第2条裂缝的距离L相距过远时,会导致水平地应力数值相近条件不足,而使中间裂缝也起裂扩展成为渗流效果较差的双翼型裂缝。 另一方面,当第1条和第2条裂缝距离过近时,若在其间再次起裂第3条裂缝时,会使裂缝间应力叠加作用过于强烈,各裂缝之间相互剧烈争夺缝宽致使起裂延伸压力过高,甚至根本无法起裂而导致储层改造效果同样不佳。 如图6所示,如果在间距为L的两条裂缝之间再次起裂第3条裂缝时,为了使第3条裂缝延伸时能够形成网状裂缝,需保证第1和第2条裂缝之间有一段应力场重塑区域符合上式的条件,其计算过程可参照图7。找出当应力场重塑区的长度S获得最大值时所对应的第1条和第2裂缝间距Lopt,此时最优裂缝间距值可用方程表示为 (11) 图6 双缝间应力改善区分支状裂缝形成示意图Fig.6 Schematic diagram for the formation of branch cracks in stress improved area between two fractures 图 7 射孔簇距优化方法示意图Fig.7 Schematic diagram of perforation cluster spacing optimization method 以中国南部某页岩气井水平井段储层为例,原地应力σh=40 MPa,σH=45 MPa,缝内压力p=45 MPa,μ=0.22,两条裂缝缝高均等于页岩储层的厚度,H1=H2=60 m,通过对所取岩心进行三轴应力破坏实验求得临界改造地应力差值K=0.5 MPa,对第1、2裂缝间距取几组不同值,依次联合进行迭代求解,满足不等式条件的应力区间长度S如表1所示,画出第1、2裂缝分布取得最优值的总水平地应力差值曲线如图7所示,此时满足应力差区间[0<φ(L)<0.5 MPa]的距离S取得最大值Smax=50.78 m,此时Dopt=0.5L=34.0 m即为最优的射孔簇间距值。 表1 不同裂缝间距下符合形成复杂裂缝应力差条件的地层区间长度对应表 根据射孔簇间距优化的方法,可以根据诱导应力来计算求取第1级压裂的最优裂缝间距Dopt1。 从趾端开始第1级压裂段的长度可表示为 L1=n1Dopt (12) 而当进行第m级压裂时,前m-1(m≥2)级压裂所产生裂缝的诱导应力改变了第m级的水平应力状态,故而在算第m级的簇间距时,需要将前m-1级压裂所生成的诱导应力叠加到第m级压裂储层的主应力之上,以新的复合应力作为初始应力代入第2部分所阐述的模型中,求解得出第m级的射孔簇间距值。这里假设水平井沿着最小主应力方向钻井,以水平井的趾端为坐标原点,建立直角坐标系,如图8所示。 式(12)中设第k级压裂段的射孔簇数为nk,那么当开始第m级压裂时(m≥2),前m-1级所有射孔簇总数为 N=n1+n2+…+nm-1 (13) 假设这N个射孔簇所起裂裂缝缝高均相同,根据线弹性力学理论,第m级压裂段射孔簇处的复合应力的大小同样可以采用应力叠加的方式获得,假设其所在横坐标为x,那么在第m级压裂段射孔簇的水平最大主应力方向复合应力可表示为 σHc(x)=σH+σay1(x)+σay2(x)+…+σayN(x) (14) 水平最小主应力方向复合应力可表示为 σhc(x)=σh+σax1(x)+σax2(x)+…+σaxN(x) (15) 式中:σayi(x)为第i个水力裂缝在第m级压裂段所产生的沿最大主应力方向的诱导应力;σaxi(x)为第i个水力裂缝在第m级压裂段所产生的沿最小主应力方向的诱导应力。 此时将新计算的最大和最小方向的复合水平主应力代入第2节所述的计算模型中,以此计算求出各个压裂段的最优射孔簇间距的值。 在逐级压裂的过程中,由于前面各级水力裂缝的干扰作用,后面各级的起裂压力和最终的闭合关井压裂也会逐级增加。 图8 水平井用于分段压裂的分簇射孔分布示意图Fig.8 Distribution diagram of cluster perforation for staged fracturing in a horizontal well 对于裂缝内部的压力,可以通过改变排量和液体黏度来调节,研究[41-42]表明,裂缝内部的泵注压力与黏度和排量的乘积μQ相关,由于高黏度对形成复杂裂缝不利,故而采用大排量可以调节裂缝内部的净压力。而对于排量和黏度已经固定的地层来说,裂缝内部所能达到的净压力pnet往往保持相对固定(略高于地层抗拉强度),通过现场施工压力曲线即可很容易获得。 本文中所提到的簇间距设计方法可以在缺少地下各个水平井段详细储层信息的情况下,通过较为简单的设计并结合水力压裂施工经验参数(缝内净压力)即可获得最优的射孔簇间距。通过长庆油田现场长6致密砂岩气储层水平井多级压裂取得了良好的试验效果。该簇间距优化方法的使用使得油田储层改造效果进一步得到改善,通过微地震显示,水力压裂裂缝的复杂度进一步提高,单井平均增幅可达6%。 如何设计水力裂缝间距使压裂时尽可能形成复杂缝网是储层改造设计的关键问题。水力裂缝的形成会在裂缝周围产生诱导应力使得储层的应力差异(σH-σh)得到改善。根据单条水力裂缝诱导应力的解析解提出了一种简便的裂缝间距设计方法,从而能最大限度促进复杂缝网形成。以平面二维水力裂缝的线弹性应力场为基础,采用应力叠加的方式来计算,通过调整水力裂缝间距将储层应力差(σH-σh)缩小至能够形成缝网的范围以内,构建最佳的射孔簇间距。 (1)水力裂缝所产生的诱导应力能够部分抵消原始水平地应力差异性,当原始水平主应力差(σH-σh)较小时能够在储层中产生应力反转现象,此时应力翻转区边界所控制的区域宽度就是最优射孔簇间距值。 (2)当单条水力裂缝不足以使水平应力(σH和σh)方向发生反转时,可通过两条裂缝间诱导应力的叠加协同效应,将裂缝间的地层的水平地应力差降低至复杂裂缝形成的门限应力差K以下,最终使新插入的射孔簇能够形成网状裂缝,根据该思路,通过本文的模型求解出该种应力状态下的最优簇间距值。 (3)当进行多级压裂时,下一级压裂的应力场可以通过前面所有水力裂缝所产生的诱导应力依次相互叠加获得,然后再根据前述的方法进行该级压裂段的裂缝间距优化。2.3 高应力差储层的射孔簇间距优化

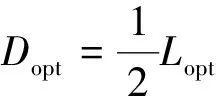

3 多级压裂的裂缝间距优化

4 讨论
5 结论
——以淮南矿区为例

