基于车车通信的前向碰撞预警策略
惠 飞,邢美华,郭 静,唐书宇
(长安大学信息工程学院,西安 710064)
(*通信作者电子邮箱xingmeihua@chd.edu.cn)
0 引言
近年来,交通事故造成了巨大的人员伤亡和经济损失,使之成为各国面临的一个严峻问题[1]。据美国高速公路安全管理局(National Highway Traffic Safety Administration,NHTSA)统计,2018年有36 560人死于车辆碰撞事故,且前向碰撞占据约30%,其中,大部分碰撞事故是人为因素造成的[2]。因此,有效检测和避免前向碰撞的预警系统对提高道路安全性具有重要意义。
前向碰撞预警(Forward Collision Warning,FCW)系统可以分为两种:一种基于毫米波雷达、激光雷达、摄像头等传统传感器感知并获取前方车辆信息;另一种通过车车(Vehicleto-Vehicle,V2V)通信实现车辆间运动、轨迹信息交互。尽管前者的精度较高且研究起始时间较早,但是存在一定缺陷,如:基于激光雷达的系统在雨、雪、雾等恶劣天气中无法稳定运行[3];激光雷达系统和雷达系统的检测都在视距(Line-Of-Sight,LOS)范围内,并且通常是定向的[4];摄像头在隧道中由于光线不足、天气因素导致视线范围缩小等。相对而言,车车通信方式不易受天气、光线等影响且能实现对非视距车辆的感知,所以,基于车车通信的碰撞预警系统成为了近年来研究的热点。
Zardosht等[5]提出了一种基于V2V的碰撞事故决策算法,并根据不同场景给驾驶员提供预警建议;Li 等[6]提出了一种基于V2V 的追尾预警系统,该系统基于风险感知来识别危险,当系统检测到不安全的行驶速度时给驾驶员发出减速警告;Xiang 等[7]分析了专用短程通信(Dedicated Short Range Communication,DSRC)作为V2V 通信方式的优势,并建立了一种基于车辆动力学和神经网络的多级预警系统;王婷婷[8]提出了一种基于DSRC 和差分全球定位系统(Differential Global Positioning System,DGPS)的协同FCW 系统,并建立了前车静止、匀速、减速三种场景下的碰撞避免模型;Zhao 等[9]提出了一种基于DSRC 的多源误差补偿的最小安全车距模型,并设置了不同级别的预警策略。
上述研究大多基于DSRC 的车车通信技术且假定延时时间内后车匀速运动。无线上网(Wi-Fi)、DSRC、长期演进技术-车辆(Long Term Evolution-Vehicle,LTE-V)和红外通信等无线通信技术均可用于V2V 通信[10]。目前,LTE-V 以其支持车辆应用具有高可靠性、大带宽[11]、全球部署、可快速实现商业化[12]等特点受到了广泛关注。因此,本文设计了基于LTEV2V 通信的FCW 系统,分析了该系统的主要延时时间,并建立了修正GPS误差并考虑主(后)车延时时间内运动状态的碰撞避免模型;针对远(前)车匀速、加速、减速不同场景给出了相应的预警策略,通过Matlab 仿真实验验证了报警策略的有效性以及考虑延时时间内主车运动状态的必要性,并针对主车延时时间内加速的情形,对提出的预警策略正确避撞率进行了验证。
1 系统结构
LTE-V 包括LTE-V 集中式(LTE-V-cell)和LTE-V 分布式(LTE-V-direct)两种模式(如图1)。与IEEE 802.11p 相比,LTE-V-Direct 是一种新的分散式架构,它对时分-长期演进技术(Time Division Long Term Evolution,TD-LTE)物理层进行了修改并尽可能保留其通用性以提供短距离直接通信、低延迟和高可靠性。据Chen 等[11]的研究,LTE-V 被视为基准模式并可以作为DSRC 的一种替代方案。通过车辆之间的实时信息共享,每辆车都可以获得周围环境的当前信息,这为道路安全和交通效率应用奠定了基础。LTE-V-Direct 用于在车辆之间直接交换与道路安全相关的低延迟安全服务信息。由于FCW 是典型的与安全相关的低延迟场景,因此本文仅关注LTE-V-Direct模式。

图1 LTE-V通信的两种模式Fig.1 Two modes of LTE-V communication
基于LTE-V 的FCW 系统(如图2)可以被分为四个部分:数据采集模块、LTE-V 设备通信模块、算法执行模块以及预警与控制模块。数据采集模块通过车辆控制器局域网络(Controller Area Network,CAN)、GPS 和加速度计等传感器获得车辆的运动学特征(如经纬度、速度、航向角、加速度等);LTE-V 设备通信模块负责广播和接收基本安全消息(Basic Short Message,BSM);算法执行模块利用主、远车信息进行当前危险状况判断并给出预警策略传送至预警与控制模块,其中,主(后)车信息通过蓝牙模块直接获得,而远(前)车信息通过接收远车LTE-V设备广播的BSM获得。
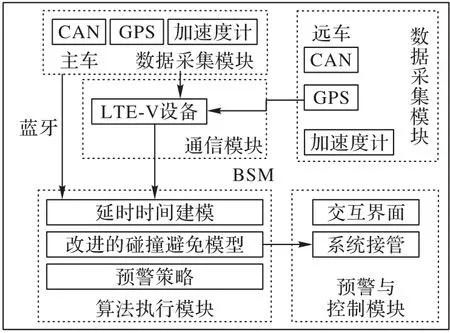
图2 基于LTE-V通信的FCW系统框架Fig.2 Framework of the FCW system based on LTE-V communication
2 延时时间建模
通过第1章中分析基于LTE-V通信的FCW 系统的整体构成如图3 所示,考虑系统中的主要延时信息获取时间、信息传输时间、警告生成时间和驾驶员反应时间对延时时间用高斯模型进行建模。
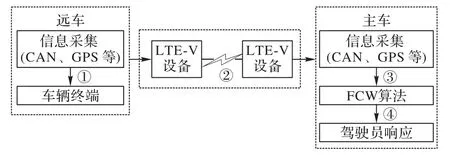
图3 基于LTE-V的FCW系统信息传输流程Fig.3 Information transmission process of FCW system based on LTE-V
2.1 数据获取时间
数据从CAN、GPS 和加速度计等传感器采集并发送到车辆终端的周期为Tc(单位:ms)。车载终端整合收集到的信息并采用ASN.1方式将信息编码形成BSM。基于LTE-V通信的BSM 发送周期为TBSM(单位:ms)。信息采集周期小于BSM 的发送周期,所以将信息获取时间表示为:

2.2 信息传输时间
LTE-V2X 通信系统分为基于SideLink(SL)的V2X 工作模式、基于UpLink(UL)或DownLink(DL)的V2X 工作模式以及中继V2X工作模式[13-14]。基于SL的V2X工作模式通过PC5接口可以高效地实现车辆间信息的直接交换。在此模式下,信息传输延时指远车通过SL 链路发送V2X 消息到主车所需的持续时间[15]。具体来说,该传输延时时间Ttrans分为:
1)远车用户设备(User Equipment,UE)等待SL链路调度周期Twait;
2)远车UE 接收SL 链路控制信息(Sidelink Control Information,SCI)传输时间TSCI;
3)远车UE 通过SL 链路将数据传输到主车UE 所用时间Tdata;
4)主车UE 解码接收信息所需时间和主车UE 高层协议栈解码所需时间Tprocess。

用描述信息传输时延的最小单位——传输时间间隔(Transmission Time Interval,TTI)描述上述过程,其中一个缩短TTI 对应0.5 ms,那么延时时间取值范围为57.3~91.1 ms[15],用高斯分布对信息传输时间进行建模,Ttrans为随机变量,服从,按照3σ原则,有:
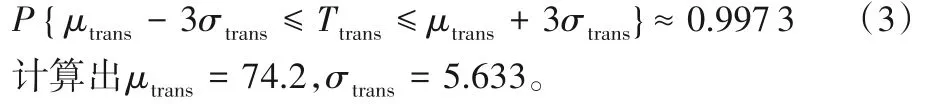
2.3 警告生成时间
主车中整个FCW 算法的执行包括处理接收到的信息(如将接收到的BSM 消息中经纬度转化为适合算法建立的XY 平面坐标、存储一定时间内的历史数据用于拟合车辆历史轨迹),根据处理后的信息确定远车所处车道,与主车的前后位置关系,建立碰撞避免模型给出预警策略并最终生成警告。警告产生的延迟指从主车接收到远车的BSM,执行FCW 算法生成警告的时间Tgen。
2.4 驾驶员反应时间
驾驶员的反应时间Tresp指从收到警告信息至踩下制动踏板的时间。驾驶员的反应时间受驾驶员的状态、车速和目标状态等因素影响很大,因此难准确确定。根据Zhao 等[9]的驾驶员反应时间测试实验,结果表明反应时间阈值边界为0.6~1.6 s。用高斯分布对驾驶员反应时间进行建模,Tresp为随机变量,服从Tresp~N(μresp,σ2resp),按照3σ原则,有:

计算出μresp=1.1,σresp=0.167。
综上,整个FCW系统的延时时间Tdelay为:
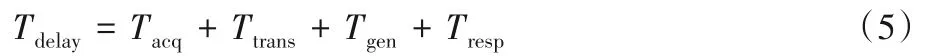
其中:信息传输时间Ttrans、驾驶员的反应时间Tresp为统计独立的高斯随机变量。那么,延时时间Tdelay仍服从高斯分布(如图4)。
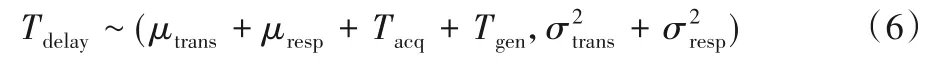
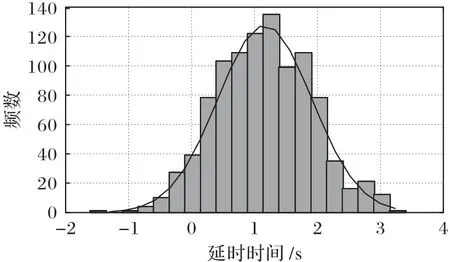
图4 延时时间高斯分布图Fig.4 Gaussian distribution of delay time
3 碰撞避免模型
为了提高预警策略的准确性,首先给出主远车的基本运动模型,然后分析GPS 误差并用圆概率误差(Circular Error Probable,CEP)进行定量表达,最后确立一种修正GPS误差并考虑主车延时时间内运动状态的碰撞避免模型。
3.1 基本运动模型
首先,确定考虑延时时间内后车运动状态的基本运动模型。假定初始时刻和主车的初始位置均为0,主、远车初始位置、速度和加速度分别记为xhv0、vhv0、ahv0、xrv0、vrv0、arv0。在延时时间Tdelay后,主车期望响应减速度记作aERD。任意时刻主车(Host Vehicle,HV)、远车(Remote Vehicle,RV)的速度、位置表达式如下:
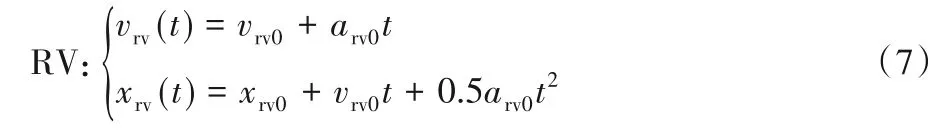
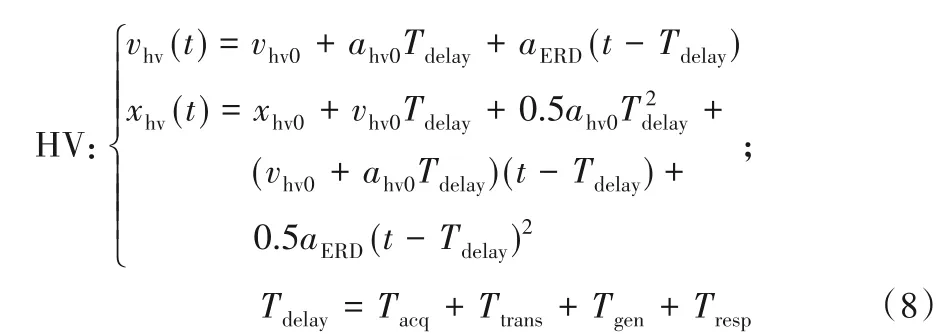
记xrel0、vrel0、arel0为初始相对位置、速度以及加速度,它们满足:

3.2 误差分析与修正
GPS 误差导致实际相对距离与理论相对位移有误差,为了进一步提高碰撞预警模型的准确性,对GPS 误差进行分析修正。
GPS 误差源包括控制段误差(如卫星钟差和卫星轨道误差)、传输误差(对流层、电离层误差)和测量误差(接收机噪声和多径)[16],所以很难为GPS 误差建立一个准确的模型,一些研究将GPS 误差假设为高斯分布[7,17],另外,还有一部分学者通过实验数据计算GPS 误差[18-19]。本文假设GPS 误差服从高斯分布:

其中:μ为均值,σ2为方差。由于误差为随机变量,所以用统计的方法圆概率误差(CEP)进行定量表达。利用圆概率误差描述定位精度在导航界广泛使用且可达到99%的置信度[20]。当概率为99%时,CEP定义为:

式中:ξCEP取值为1.522 2;σφ为二维位置坐标误差的经度方向的标准差;σλ为纬度方向的标准差。
假定二维坐标两个方向具有相同的标准差,如σφ=σλ=σ,且LTE-V设备的精度要求达到1.5 m,那么1.522 2 ×(2σ)=1.5 m,σ=0.493。μ为0,通常一个GPS 接收者不会有恒定的位置偏差[7]。那么dgps的分布函数为:

3.3 碰撞避免模型建立
由于众多经典模型[8,21-24]中均假定主(后)车在延时时间内做匀速运动,这会导致主车本身加速时低估当前风险,而在主车本身减速时高估风险。因此,本文基本运动模型中就考虑了主车在延时时间内的运动状况,又对GPS 误差进行了详细的分析。最后,将总的安全车距Ds分为车辆间相对位移xrel、误差修正项xcorr和车头时距xmin。碰撞避免模型的时序分析如图5。
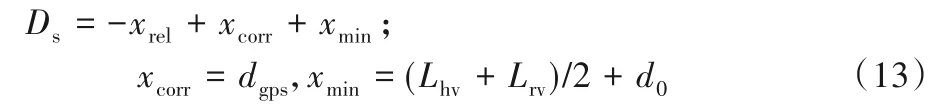
式中:Lhv、Lrv分别为主、远车车长;d0为车辆静止时应保持的最小车距。
4 预警策略
根据远(前)车的运动状况,本文将前向碰撞预警分为远车匀速(静止)、加速和减速三种场景并针对不同场景制定不同的预警策略。一般情况下,当远车加速时,碰撞的几率较低,但是当远车初始速度较小且加速度较小而此时主车速度、加速度较大时仍有碰撞的危险,所以将远车加速场景考虑在内;而减速情形又根据主车与远车减速度的相对大小分为普通减速和急减速两种情形。
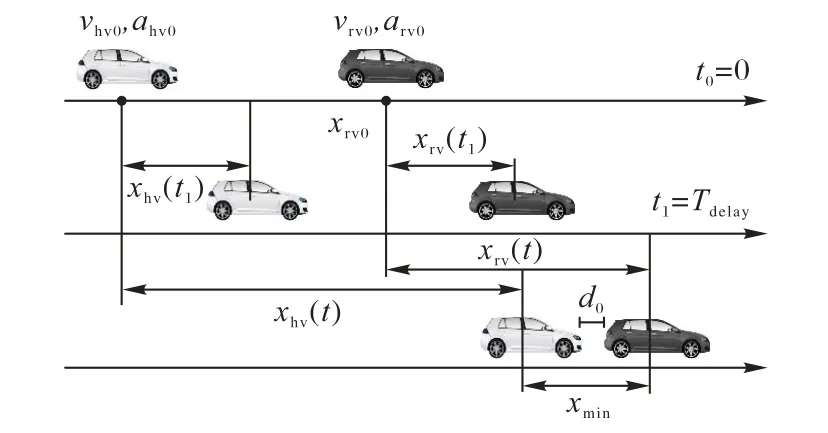
图5 碰撞避免模型的时序分析示意图Fig.5 Time series analysis diagram of collision avoidance model
4.1 远车匀速(静止)或加速
要避免主(后)车与远(前)车发生碰撞,则需满足的最基本条件是主车位移小于远车位移,结合对运动过程中不可避免的误差补偿以及车辆停止时需保证的车头间距,得到下述约束条件:

由式(7)、(8)可得,车辆间的相对运动xrel(t):
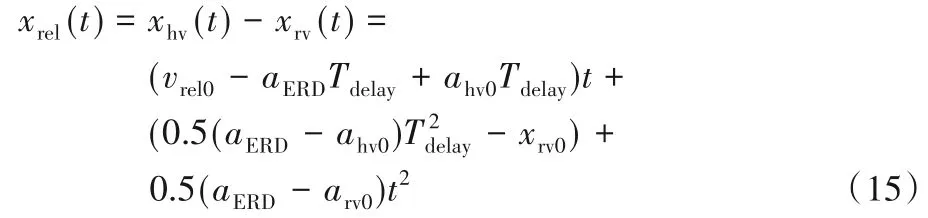
将式(15)代入约束条件式(14),得到xsafe(t)是关于t的二次函数。进一步转化,可得:
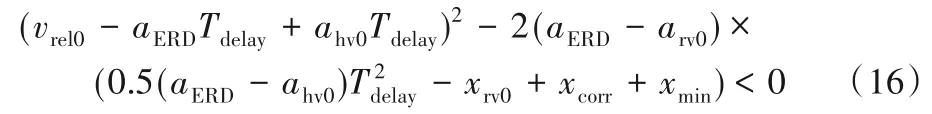
那么,通过式(16)可以得出主车制动过程需要的减速度为:

进一步地,将aERD=a1代入xsafe(t)=0,得到方程的解thv:

4.2 远车减速
设远车制动时间为trv,根据trv与thv的关系将远车减速场景分为普通减速和急减速两种情形。远车减速至0 时,trv=-vrv/arv。
1)当-vrv/arv≤thv,arv<0,表明此时主车先于远车减速至0,定义为普通减速情形。此时避免碰撞的约束条件同式(17),后车制动过程需要的减速度为aERD<a1。
2)当-vrv/arv>thv,arv<0,表明此时远车先于主车减速至0,定义为急减速。此时避免碰撞的约束条件为:

那么,通过式(16)可以得出主车制动过程需要的减速度为:
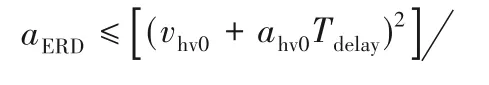

综上,不同场景的预警策略为:

其中:远车匀速(静止)、加速、普通减速的情形的策略为aERD<a1;急减速情形的策略为aERD<a2。
5 仿真与结果分析
为了验证模型的可靠性,本文运用Matlab 2016b 仿真软件对前述场景的不同情况分别进行仿真实验,结合前述的延时时间建模、GPS误差修正分析等,将仿真中必要参数的设置如表1所示。

表1 仿真参数设置Tab.1 Simulation parameter settings
由于延时时间内车辆加速时会低估当前风险、增加碰撞的可能,所以假设延时时间内主车本身在做加速运动,并针对不同场景给出相应的预警策略。图6(a)~(d)给出了对应于四种不同情形下的碰撞避免模型给出预警策略的例子。假定主车的初始位移一直为xhv0=0 m,图6(a)的初始条件xrv0=25 m,vrv0=9.72 m/s,vhv0=18.06 m/s,arv0=2 m/s2,ahv0=3 m/s2。对应远(前)车加速的情形,此时后车有较大的初始速度和初始加速度,且在延时时间后执行aERD<a1的策略,那么此时避免碰撞须采取的临界制动减速度为aERD=-3.11 m/s2。图6(b)的初始条件为xrv0=20 m,vrv0=11.1 m/s,vhv0=16.6 m/s,arv0=0 m/s2,ahv0=0.5 m/s2。对应远(前)车匀速的情形,在延时时间后执行aERD<a1的策略,避免碰撞须采取的临界制动减速度为aERD=-2.51 m/s2。图6(c)的初始条件为xrv0=15 m,vrv0=15.3 m/s,vhv0=16.6 m/s,arv0=-3 m/s2,ahv0=0.5 m/s2。对应远(前)车普通减速的情形,在延时时间后执行aERD<a1的策略,避免碰撞须采取的临界制动减速度为aERD=-5.87 m/s2。图6(d)的初始条件为xrv0=20 m,vrv0=16.6 m/s,vhv0=15.3 m/s,arv0=-5 m/s2,ahv0=0.5 m/s2。对应远(前)车急减速的情形,在延时时间后执行aERD<a2的策略,避免碰撞须采取的临界制动减速度为aERD=-5.31 m/s2。由位置关系曲线可以得出,采取上述预警策略计算的减速度可以避免碰撞。
为了验证考虑延时时间内主车运动状态(特别是主车加速的情形)的必要性,设置相同初始位置、速度、加速度条件,并对碰撞模型中的GPS误差进行修正,延时时间假定相同,此时主车在延时时间内匀速还是加速为唯一对比量。接下来分别计算获得相应的aERD,并代入前述相对车距公式计算当前车辆间的距离。图7(a)~(d)分别对应四种不同情形下的考虑与不考虑主车延时时间内车辆间的距离。其中,假定延时时间内车辆匀速运动,车辆间距曲线如实线所示;假定延时时间内车辆匀加速运动,车辆间距曲线如虚线所示。当车辆间的相对距离小于临界碰撞值,表明此时车辆会发生碰撞。图7(a)~(d)虚线表明车辆间距离始终大于碰撞阈值,而实线表明车辆间距离会小于碰撞阈值。这意味着在此种情况下不考虑主车延时时间内本身的运动状态会发生碰撞,而考虑主车延时时间内运动状态的模型可以避免或减轻碰撞。

图6 四种情形下的速度、位置关系示意图Fig.6 Schematic diagram of relationship between speed and position in four situations
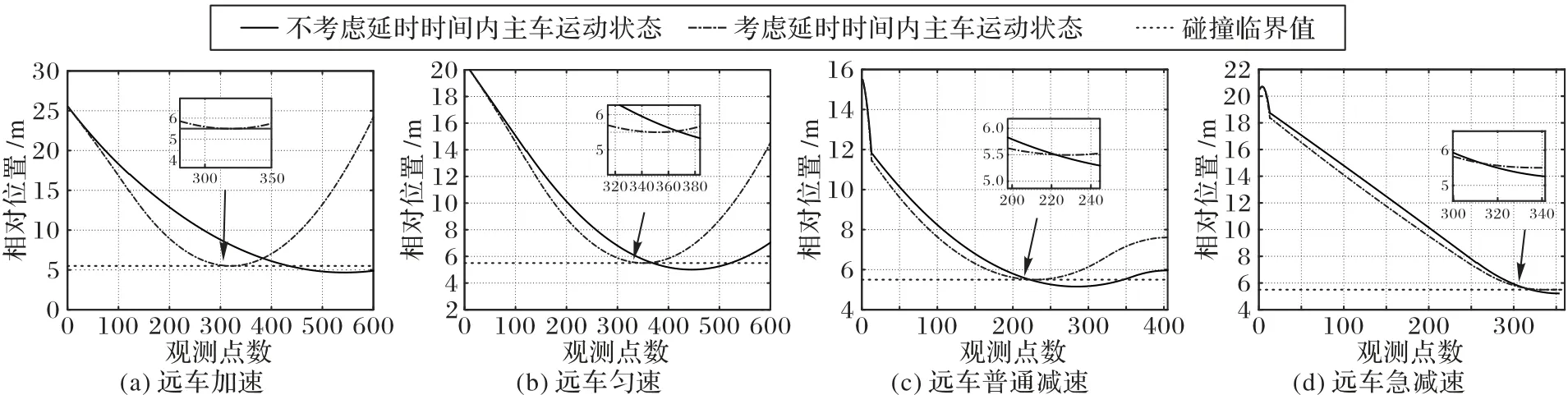
图7 四种情形下不同模型车间距离比较Fig.7 Comparison of distance between vehicles of different models in four situations
针对延时时间内主车加速运动的情形,初始运动状态数据设置如表2 所示,其中主车初始速度以1 km/h 为改变量进行变化,将速度加入均值为0、标准差为0.5 的高斯噪声来模拟速度的扰动,每组场景下的对应情形分别进行20 次重复实验。设N为总实验次数,能成功避免碰撞的次数为Nsuccess,那么成功避撞率Psuccess=(Nsuccess/N)*100%。按照考虑后车本身加速运动状态所制定的aRED,将其代入到相对运动公式,判断出是否会发生碰撞并通过多次实验计算成功避撞率。进一步地,为了考虑延时时间对预警策略的影响,在第2 章对延时时间进行高斯建模的基础上,将延时时间设置初始值为1.19 s,然后加入均值为0、方差为0.031的高斯随机噪声来模拟延时时间扰动。初始运动状态数据设置仍如表2 所示,其中主车初始速度以5 km/h 为改变量进行变化,每种场景下的对应情形分别进行60次重复实验并计算相应的成功避撞率。
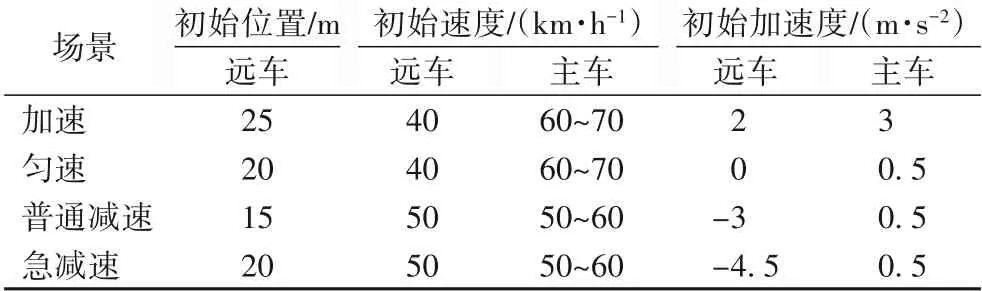
表2 运动状态参数设置Tab.2 Motion state parameter settings
图8(a)、(b)分别显示的是在对速度加入扰动和对延时时间加入扰动时四种场景下采用本文预警策略得到的成功避撞率,其中每种场景下分别列出了对应的最低值、平均值和最优值。从平均值来看,将后车延时时间内的运动状态考虑在内并制定相应预警策略,避撞率可以达到96%。
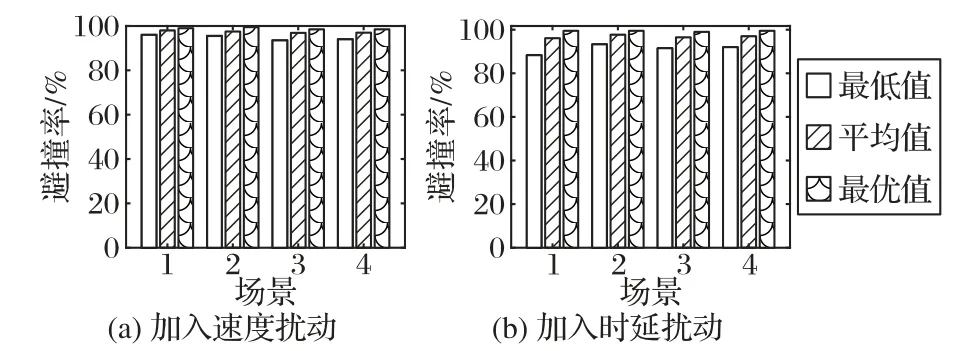
图8 四种场景下的成功避撞率Fig.8 Successful collision avoidance rate in four scenarios
6 结语
前向碰撞是当前交通事故的重要原因之一。依靠车车通信实现非视距情况下车辆间的信息交互,可以为驾驶员提供合理的碰撞预警,从而提高道路行驶的安全性。LTE-V 通信运用于车联网被认为是实现智能交通的有效途径,因此,本文提出了一种基于LTE-V 通信的前向碰撞预警设计,主要对基于LTE-V 通信的前向碰撞预警系统的整体延时时间进行建模,对GPS误差进行表达,修正并建立考虑主车延时时间内运动状态的碰撞预警模型。实验结果表明,所提出的预警策略满足不同场景下的预警需求并且可以比相同初始速度、位置以及延时时间的传统预警策略提供更安全的预警。鉴于理论分析和仿真验证的局限性,下一步将利用实际测试数据对模型进一步修正,以深入改进和提升对实际应用场景的适应性。

