考虑初衬作用的大跨储水隧洞二衬结构模型及分析
隋涛
上海市政工程设计研究总院(集团)有限公司 200092
引言
软岩区的大跨复合式衬砌隧洞结构设计时,因岩层一般较为破碎,整体性差,作用于衬砌的围岩压力主要考虑松弛压力,松弛压力由初衬和二衬共同承担,围岩对衬砌有一定的约束作用[1]。由复合式衬砌的施工工艺可知,初衬的设计,应使二衬在施工过程中长期安全,二衬施做完成后,由初衬和二衬共同承载,以保隧道结构的长久安全。
目前,进行软岩区的大跨复合式衬砌隧洞结构内力分析时,初衬、二衬的分析均以荷载-结构法为主要分析方法,同时考虑初衬、二衬的荷载承载比。《公路隧道设计细则》[2]、《公路隧道设计规范》[3]中给出了隧洞初衬、二衬各自承载分担比的范围大小,然而具体工程中的定量分析难以确定,设计承载比大多以经验为准,其可靠性不高。对于大跨隧洞设计,大多的设计者从设计安全性出发,二衬计算验算时不考虑初衬荷载分担作用[4],即二衬承担全部的围岩松弛荷载(全荷载模型)。这种方法虽简单,然较为保守。
地层结构模型尽管可以很好地模拟岩土、初衬、二衬之间的相互作用,但是其建模复杂,且其结果受围岩参数、衬砌材料参数影响显著,通常仅作为一种相互验证的手段。基于此,本文通过对初衬、二衬之间相互作用原理的分析,提出考虑初衬作用的二衬模型,并对工程案例进行计算分析。
1 基本原理
1.1 考虑初衬的二衬结构承载作用模型
复合式衬砌由初衬、防水层、二衬构成。防水层(挂板式)固定于初衬之上,二衬直接作用于防水层,二衬与初衬完全隔离,初衬、二衬之间未完全粘结,其间不具备传递剪切作用,主要表现为二者之间的受压作用,如图1所示。
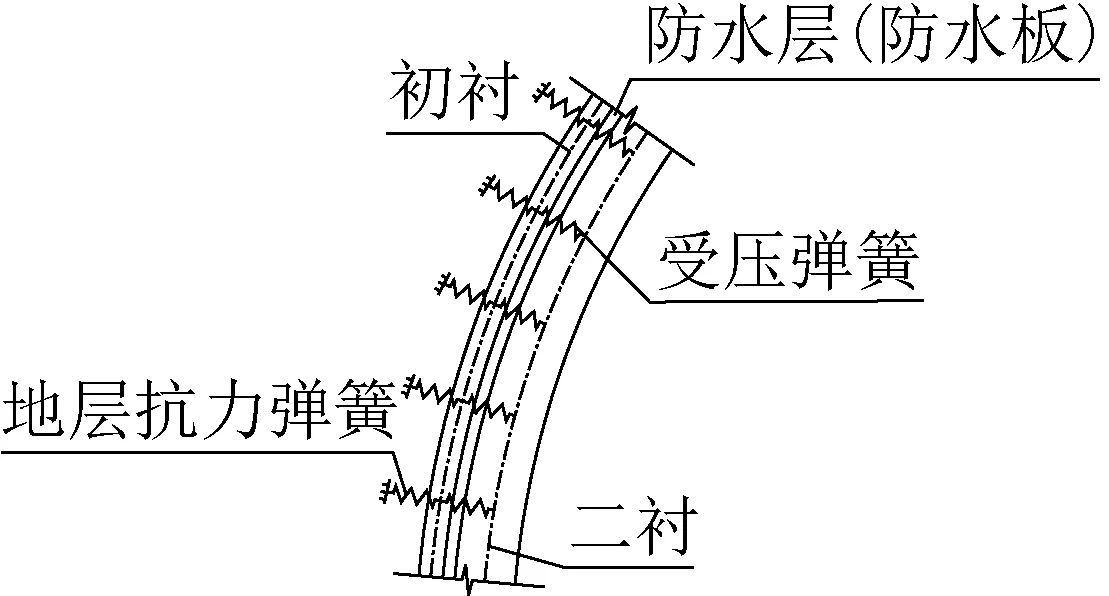
图1 复合式衬砌之间的受压弹簧模型Fig.1 Model of compression spring in composite lining tunnel
基于此,假定防水层只传递压力,不传递拉力和剪力,以受压弹簧单元进行模拟[5]。令初衬、二衬的径向变形分别为Δ1和Δ2:
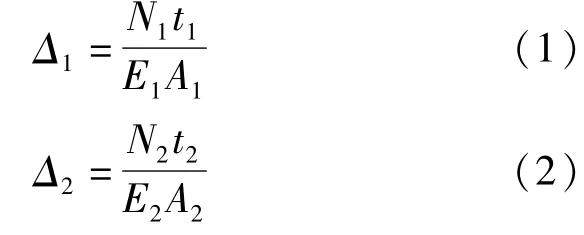
分别令Δ1=1,Δ2=1,则初衬径向变形(仅受压)弹簧刚度K1和二衬径向变形(仅受压)的弹簧刚度K2分别为:
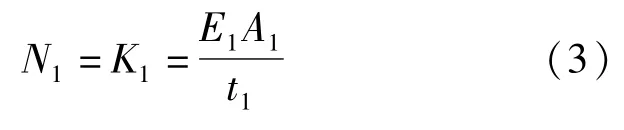
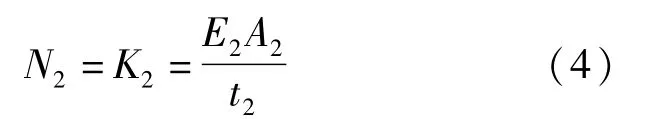
由弹簧串联后的总刚度可知,复合式衬砌的初衬、二衬之间的接触面径向弹簧抗压刚度为:
由于初衬单元与二衬单元的接触面面积相等,那A1=A2=A,则:
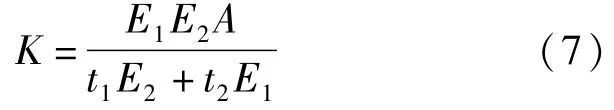
式中:E1、E2分别为初衬、二衬结构的弹性模量(kPa);t1、t2分别为初衬、二衬结构的厚度(m);A1、A2分别为初衬、二衬结构的单元接触面面积(m2);K1、K2分别为初衬、二衬结构的径向抗压刚度(kN/m)。
1.2 有限单元模型
应用荷载-结构法分析计算复合式衬砌的二衬结构的受力特征时,分析模型中主要包括初衬、二衬结构单元以及其相互作用受压弹簧单元、地层抗力单元、荷载分布。
初衬、二衬采用二维梁单元进行模拟,初衬、二衬结构单元之间的相互作用采用连接弹簧进行模拟(仅考虑压缩作用),隧洞周边岩体对隧洞结构的弹性抗力采用地层抗力弹簧模拟(仅考虑受压作用)[3],抗力大小为Fd=Kdδ,其中Fd为地层弹性抗力(kPa),Kd为弹性抗力系数(kPa/m),δ为结构变形量(m)。荷载结构法计算的模型如图2和图3所示。
图2 初衬、二衬间的受压弹簧单元示意Fig.2 Schematic diagram of compression spring elements in initial liner and the secondary liner

图3 初衬与围岩体间受压弹簧单元示意Fig.3 Schematic diagram of compression spring elements in the initial liner and rock
1.3 单元相关参数确定
根据隧洞的受力状态,以平面应变问题进行隧洞横截面的受力分析,考虑其切线方向的变形,其弹性模量修正为,ν为泊松比,钢筋混凝土结构取0.2。接触受压面积A 取纵向单位长度与衬砌单元长度的乘积,与初衬、二衬梁单元划分大小有关。
2 应用案例
2.1 工程概况
某储水隧洞为复合式衬砌结构,位于Ⅴ级围岩区,隧洞埋深30m(浅埋隧洞),隧洞由多段圆弧组成,隧洞净宽16.3m,净高16.37m初衬厚40cm(喷锚支护),二衬厚1m(钢筋混凝土),初衬、二衬之间敷设防水板,如图4和图5所示,其材料参数见表1。
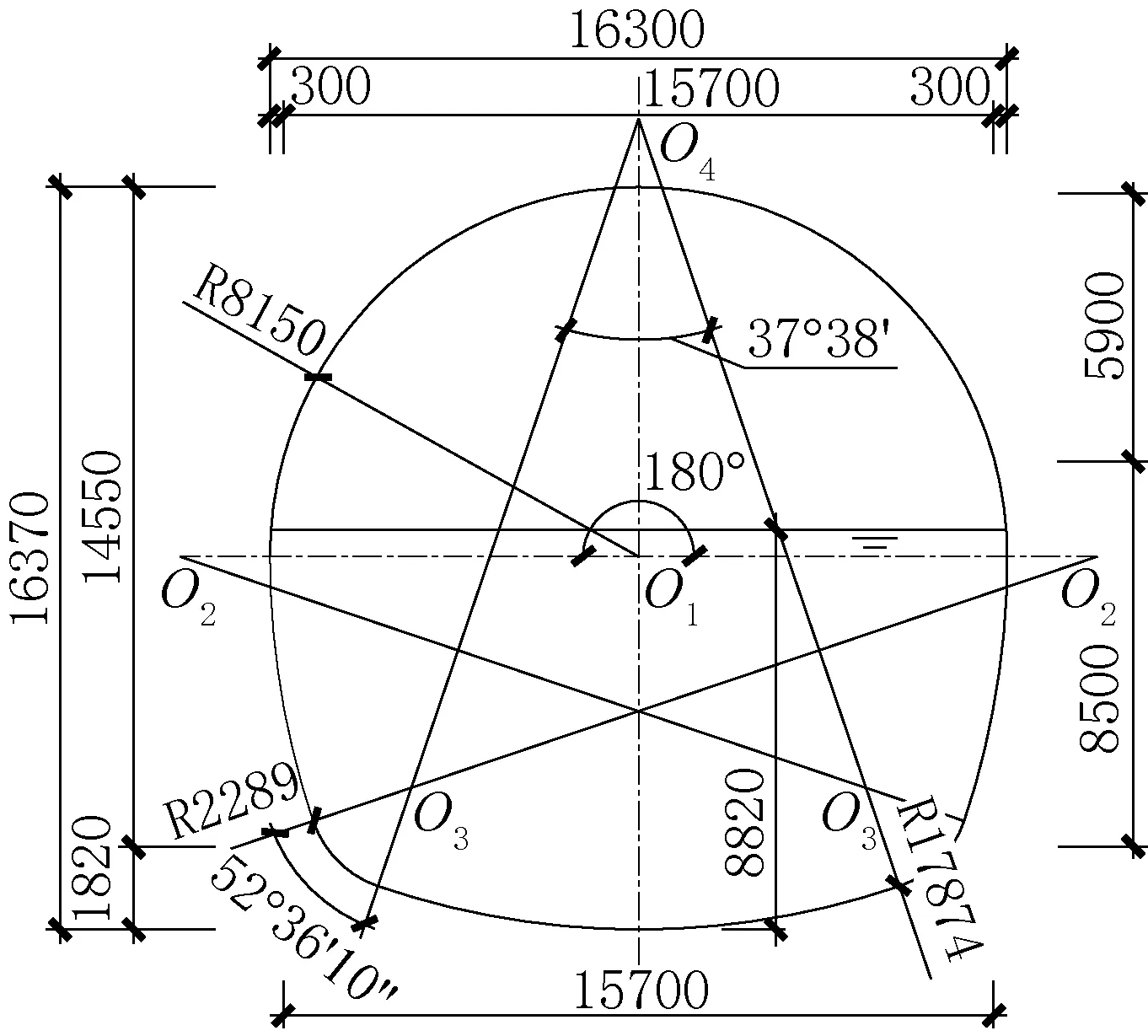
图4 隧洞内轮廓示意Fig.4 Schematic diagram of the inner outline of tunnel
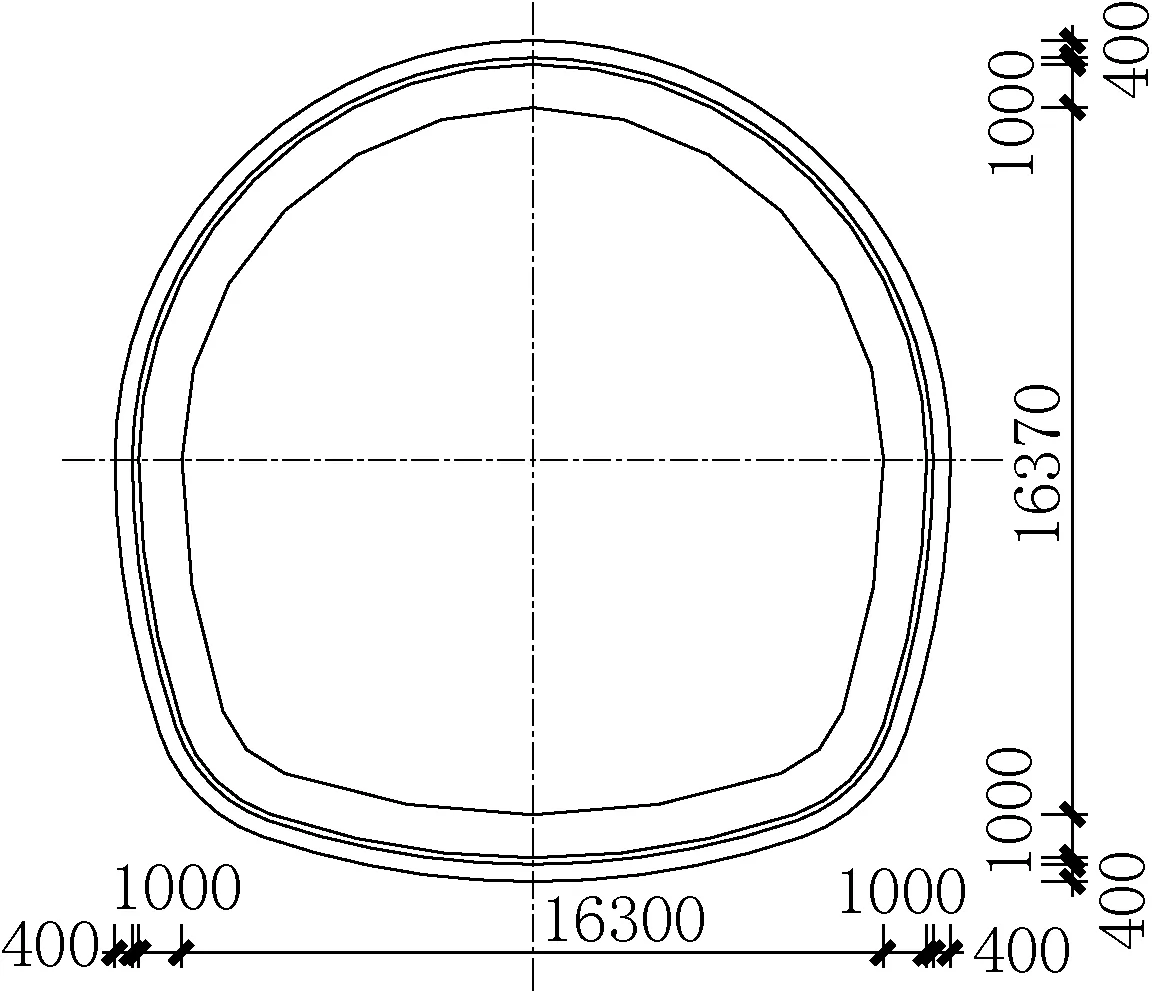
图5 隧洞断面设计示意Fig.5 Schematic diagram of the tunnel section design
2.2 计算工况
工况一,二衬计算时不考虑初衬作用,荷载全部由二衬承担,即二衬的全荷载模型;其中施工工况为二衬完成,隧洞内未储水;使用工况为隧洞内储水。
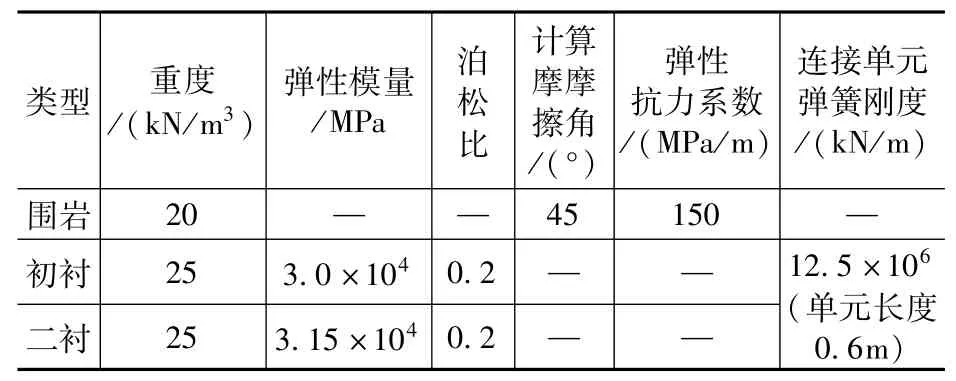
表1 初衬、二衬以及围岩材料参数Tab.1 Material parameter of the initial liner,the secondary liner and rock
工况二,二衬计算时考虑初衬作用,荷载由初衬、二衬共同承担,即考虑初衬作用的二衬模型;其中施工工况为二衬完成,隧洞内未储水;使用工况为隧洞内储水。
3 计算结果与分析
3.1 计算结果
隧洞二衬位移计算结果见图6、图7,内力计算结果见图8~图10。
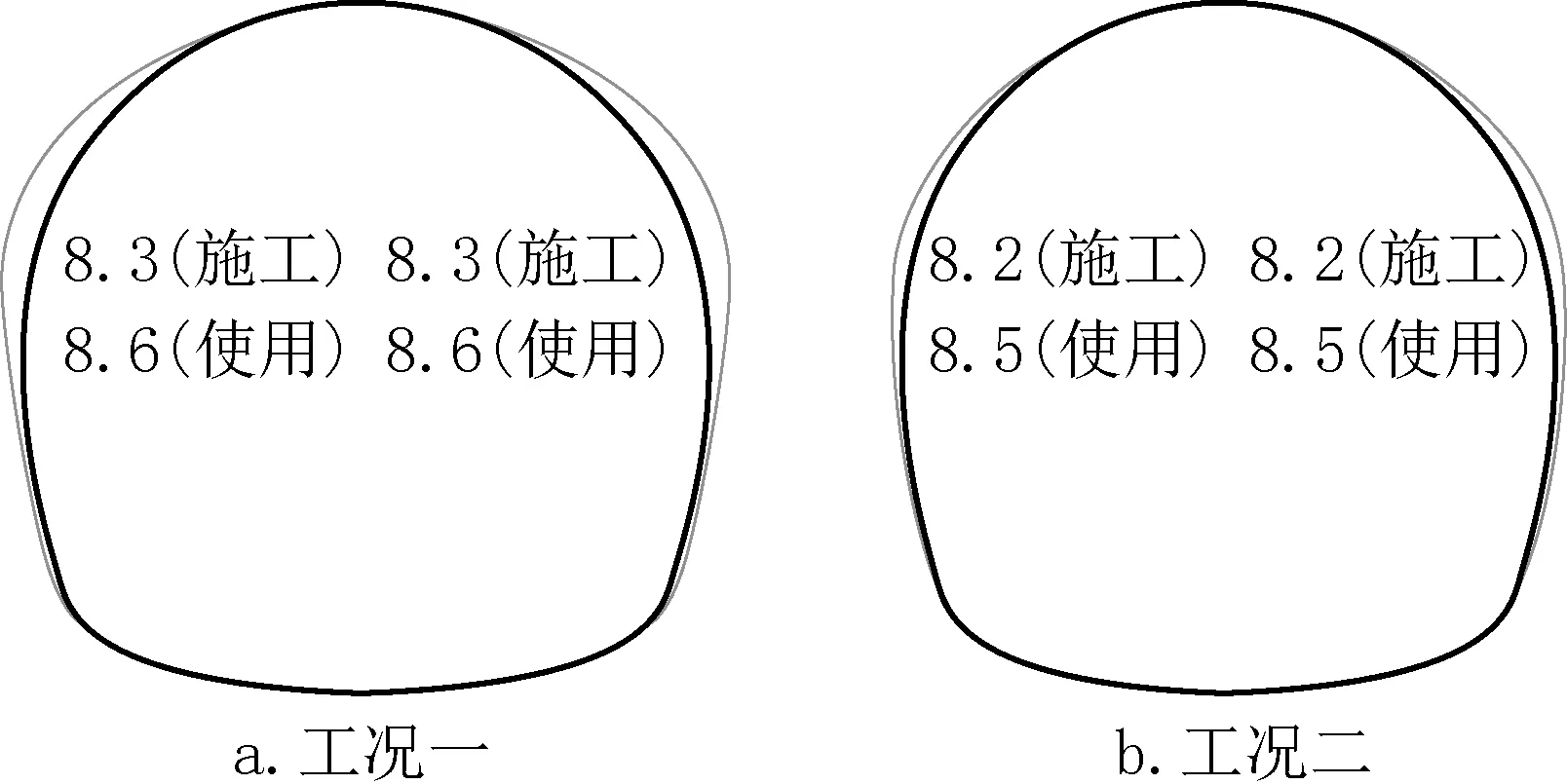
图6 隧洞水平向位移(单位:mm)Fig.6 Horizontal displacement of tunnel(unit:mm)
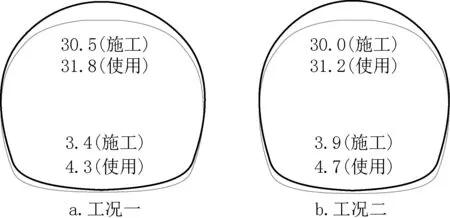
图7 隧洞垂直竖向位移(单位:mm)Fig.7 Vertical displacement of tunnel(unit:mm)
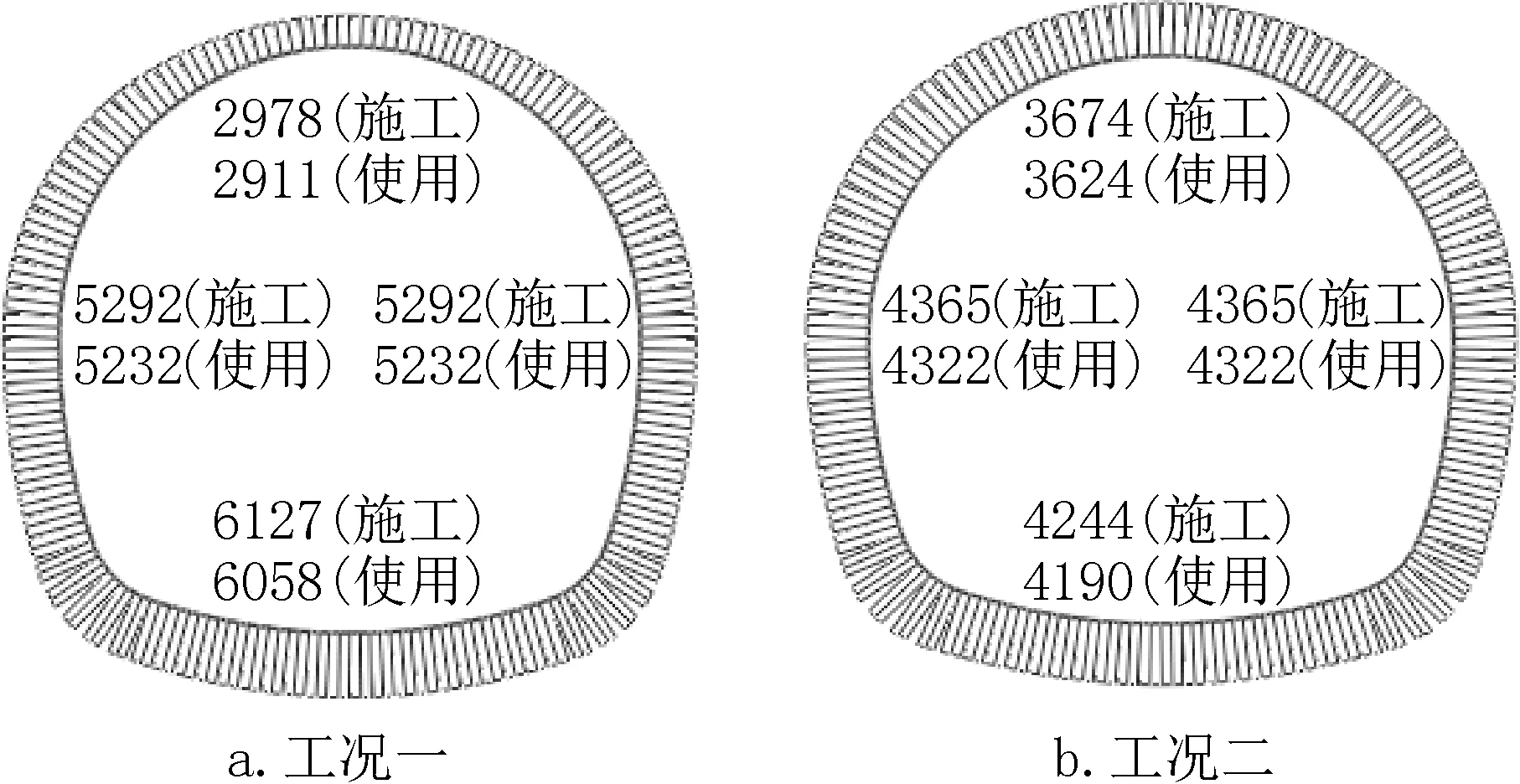
图8 隧洞轴力(单位:kN/m)Fig.8 Axial force of tunnel(unit:kN/m)
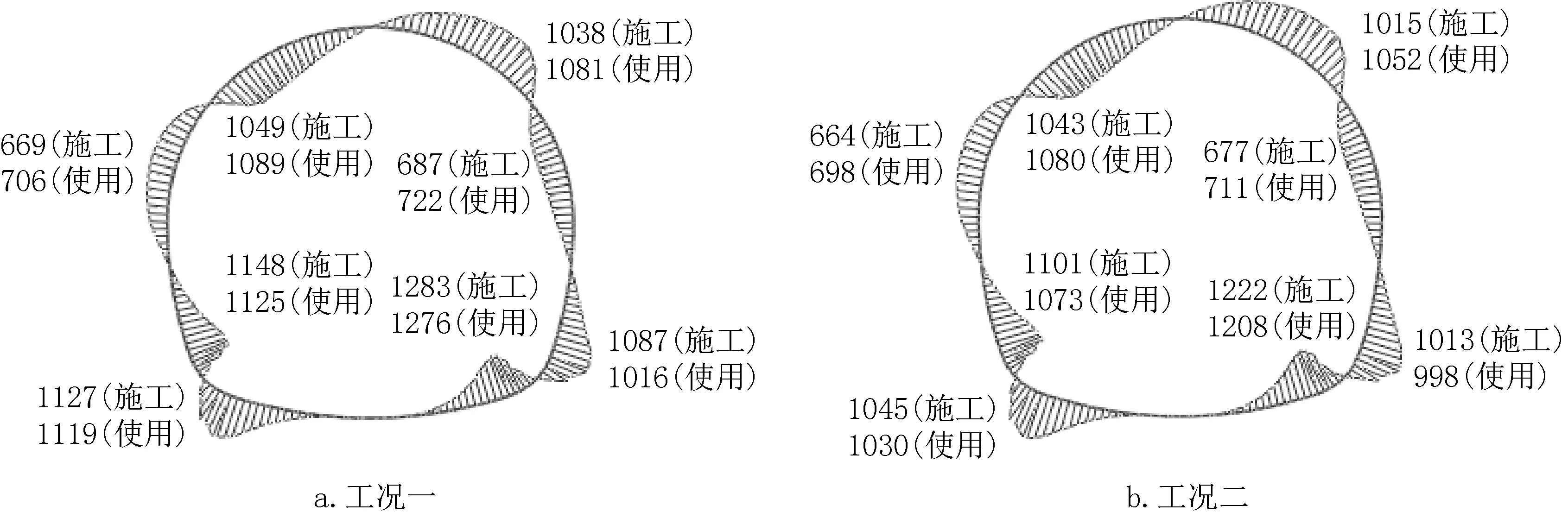
图9 隧洞剪力(单位:kN/m)Fig.9 Shear of tunnel(unit:kN/m)
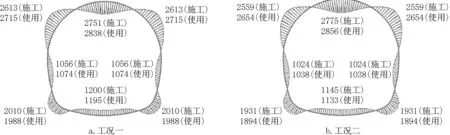
图10 隧洞弯矩(单位:kN·m/m)Fig.10 Bending moment of tunnel(unit:kN·m/m)
3.2 结果分析
1.隧洞二衬位移的变化特征
(1)工况一时,由于使用工况的隧洞内水压作用,储水使用工况位移较施工工况时位移大,拱腰处水平位移相差0.3mm;拱顶处垂直位移相差1.3mm,仰拱处垂直位移相差0.9mm。
(2)工况二时,由于使用工况的隧洞内水压作用,使用工况位移较施工工况时位移大,拱腰处水平位移相差0.3mm;拱顶处垂直竖向位移相差1.2mm,仰拱处垂直竖向位移相差0.8mm。
(3)施工工况时,工况一的拱腰水平位移、拱顶竖向位移较工况二大,相差分别为0.1mm和0.5mm,仰拱垂直竖向位移较考虑初衬作用时小,相差0.5mm;使用工况时,工况一的拱腰水平位移、拱顶垂直竖向位移较工况二大,相差分别为0.1mm和0.6mm,仰拱垂直竖向位移较考虑初衬作用时小,相差0.4mm。
2.隧洞二衬内力的变化特征
(1)工况一时,隧洞轴力总体的变化趋势为使用工况较施工工况时小,但相差较少,最大相差2.2%(拱顶);隧洞剪力变化显著处为底板与侧壁交接处,且使用工况较施工工况时小,最大相差约6.5%;隧洞弯矩除底板、底板与侧墙相交处外,其余各处的弯矩均为使用工况较施工工况大,其中拱腰相差最大,相差为3.9%;引起轴力、剪力、弯矩前后变化主要为使用工况时内水压力抵消了部分隧洞外侧的围岩压力,但由于围岩弹性抗力的存在,水压力较其引起的变化很小,所以隧洞内力在两种工况前后的变化较小。
(2)工况二时,隧洞二衬结构轴力总体的变化趋势为使用工况较施工工况小,但相差较少,最大相差1.4%(拱顶);隧洞剪力变化显著处为底板与侧壁交接处,且使用工况较施工工况时小,最大相差约4.8%;隧洞弯矩除底板、底板与侧墙相交处外,其余各处的弯矩均为使用工况较施工工况大,其中拱腰相差最大,相差为3.7%。
(3)由于隧洞结构初衬分担作用,隧洞二衬结构轴力工况一和工况二的计算分析结果变化较大,除拱部外,其余各处的轴力在各工况下采用全荷载模型较考虑初衬作用时均减小,且变化大,最大相差约31%(底板),拱部变化相差约24%(增大)。隧洞结构剪力工况一和工况二的计算分析结果变化较小,且各处的剪力在各工况下采用全荷载模型较考虑初衬作用时均减小,且变化小,最大相差约8%(底板与侧墙相交处)。隧洞结构弯矩工况一和工况二的计算分析结果变化较大,除拱顶外,其余各处的弯矩在各工况下采用全荷载模型较考虑初衬作用时均增加,变化最大处为侧墙与底板相接处,变化相差约5%。
4 结论
1.考虑初衬作用计算的二衬结构位移较全荷载模型大,两者前后相差约15%。
2.考虑初衬作用计算的二衬结构轴力除拱顶外,均小于全荷载模型计算结果,且两者相差较大,约31%;二衬结构弯矩除拱部,其余各处均小于全荷载模型计算结果,最大相差约5%。
3.考虑初衬作用计算分析时,初衬对轴力、弯矩和剪力均有不同程度的承载分担作用,但是对轴力的分担作用最多,充分说明了隧洞二衬施工后,初衬一定程度上承担了围岩的作用力,二衬设计时,应考虑初衬承担的作用。
4.二衬全荷载模型设计概念简单、明确,但是过于保守,且若考虑初衬作用时,需根据经验设置二衬的承载比,可靠性不高;考虑初衬作用的二衬计算模型概念清晰,且避免了人为经验因素考虑的初衬、二衬的分担作用,可作为隧洞设计验算的一种方法。

