亚热带日本落叶松人工林立地指数表编制1)

刘柄昂 彭湃 马丰丰

(湖南省林业科学院，长沙，410004)

宋庆安 袁穗波 吕勇 向祖恒 冯骏 苏尚敏

(湖南省林业科学院) (中南林业科技大学) (龙山县林业局) (湖北省长岭岗林场) (湖北省高岩子林场)

在林分树高生长样本函数空间中，林分立地质量因子的作用是不容忽视的，它不能看成随机因子，随着林龄的增长，对林分树高生长的影响逐渐显现，由于树高较易测定，受林分密度影响较小，利用林分优势高早已成为林业上最常用的评定立地质量的方法[1-2]。立地指数是指在某一立地上特定基准年龄时林分优势木的平均高度值[3-4]，常用的编表方法有标准差调整法[3-5]、变动系数调整法[5-6]、相对优势高法[7-9]、差分方程法[10]，其中，标准差调整法和相对优势高法应用较为广泛[3]。

日本落叶松(Larixkaempferi(Lamb.) Carr)，松科，落叶松属，落叶乔木，原产于日本本州岛中部山区，目前在中国，其人工林栽培区已十分广阔，北起黑龙江省林口县，南至湖南省城步县和四川省雷波县，范围大约在北纬26°20′～45°15′，东经101°28′～130°50′，涉及14个省市(区)[11]。与同区华北落叶松、长白落叶松等乡土落叶松相比，日本落叶松表现出较高的生长量、巨大的生产潜力及广幅的生态适应性等优点[12]。随着造林地点的南移，日本落叶松显示出的生长优势也越大[12-13]。亚热带海拔1 000 m以上的中山地区是我国日本落叶松最适宜引种区，已发展成为我国新的落叶松速生丰产林基地，目前该区累计推广造林面积超过33.3万hm2[14]。

关于日本落叶松立地指数的研究已有一定基础，如凌远云等[15]90年代初以理查德函数为基本模型、鄂西山区50株优势木解析木数据为基础编制了鄂西日本落叶松人工林的多形地位指数表；2001年马友平等[16]以150株日本落叶松优势木平均高为基础，运用8个回归曲线模型拟合出最佳导向曲线，以比例法编制了长岭岗日本落叶松的立地指数表；肖蓉萍等[17]于2004年编制了豫西伏牛山区日本落叶松人工林的地位指数表。本文以亚热带湘西、鄂西山区日本落叶松人工林为研究对象，涵盖该区域日本落叶松所有立地类型，编制亚热带日本落叶松人工林的立地指数表，评价其立地质量，以期为该地区日本落叶松的造林营林、资源数据调查提供切实可行的依据[17-18]。

1 研究区概况

研究地位于亚热带湘西、鄂西山区日本落叶松主要引种区。湘西龙山县处于云贵高原东端，地理位置为109°13′～109°46′8″E，28°46′7″～29°38′4″N，地形地貌上多为中、低山峡谷和低山丘陵峡谷谷地形态，局部为山间谷地平原。山脉走向多呈北偏东22.5°～北偏东45°延伸，山顶海拔最高为1 736 m(万宝山)，1 000 m左右的山峰较多，年降水日177～200 d，降水量1 571.4～1 677.0 mm，土壤主要为山地黄棕壤及山地黄壤，土壤疏松，透气性好，水分含量适中。气候温和，雨量充沛，雨热同季，植被生长旺盛，适宜培育大径木材[19]；鄂西建始县地理位置为108°21′～110°58′E，29°27′～31°57′N，由秦岭山脉东延部分的武当山、大巴山、荆山山脉以及云贵高原东延部分的齐岳山、八面山、武陵山脉组成。海拔起伏较大，属北亚热带季风气候区，年降水量1 000～1 200 mm，土壤属于红黄壤与黄棕壤地带，该区植被类型丰富，除典型的亚热带常绿阔叶林外，山地垂直带上还有混交林、亚高山暗针叶林及落叶阔叶林等植被类型，同时，独特的气候条件非常适合日本落叶松人工林的引种和栽植[20-21]。

湖北省20世纪50年代开始引种，主要分布于鄂西山区，包括恩施土家族苗族自治州(利川市、宣恩县、鹤峰县、恩施市、建始县、巴东县)，宜昌市(秭归县、长阳县、五峰县、宜都市、兴山县、宜昌市)，神农架林区和襄阳市(保康县、谷城县)，海拔分布范围为1 000～2 000 m，鄂西北十堰市、鄂东北大别山区以及鄂东南幕阜山区有零星分布[22-24]。湘西土家族苗族自治州龙山县2000年从湖北建始县开始引种，引种营林470 hm2，引种育苗3.3 hm2，主要分布于龙山县万宝山林场、八仙洞林场[19]。

2 材料与方法

2.1 资料收集与预处理

根据亚热带湘西、鄂西地区日本落叶松人工林营林情况，课题组于2008、2018年在湖南省湘西州龙山县万宝山林场、八仙洞林场；湖北省恩施州建始县长岭岗林场、高岩子林场布设固定样地和临时样地274块，样地面积为200～600 m2，分布于日本落叶松人工林各种立地类型及各个年龄的林分中，如表1、表2所示。选测优势木采用每100 m21株，根据布设样地面积选取优势木株数及树高，并以其平均高作为优势高[1]。根据上述方法调查获得优势解析木29株，胸径分布在3.0～50.0 cm，树高在4.0～35.5 m。优势解析木年龄分布于8～33 a，树高范围6.0～23.0 m，胸径范围7.1～31.8 cm。

表1 日本落叶松不同立地因子分类[24]

表2 不同立地类型及林龄日本落叶松分布情况

对样地调查数据按龄组(龄阶=2 a)分别统计计算出平均林龄和优势木平均高，且用下式计算各龄阶的树高标准差：

式中:Si为第i龄阶树高标准差；Hij为第i龄阶中第j株优势木树高(j=1,2,…,ni)；ni为第i龄阶中优势木株数或标准地数。

2.2 导向曲线的选取

在林分优势树高生长曲线簇中，有一条代表在中等立地条件下，林分优势树高随林分年龄变化的平均高生长曲线，该曲线为导向曲线[1]。根据散点分布趋势，采用下列常用的数学模型作为导向曲线模型：

对数双曲线式lg(H)=a+b/A；

对数曲线式lg(H)=a+blg(A)，H=a+blg(A)；

抛物线式H=a+bA+cA2；

单分子式H=a(1-e-bA)c；

理查兹式H=a(1-be-cA)1/(1-m)；

双曲线式H=a+b/A。

式中：H为林分优势木平均高，A为林分年龄，a、b、c、m为待定参数[1]。

表3 优势木平均高龄阶统计

2.3 精度检验方法

利用29株日本落叶松优势木解析木数据，通过计算平均误差(EM)、平均相对误差(E)、平均绝对相对误差(EMA)、预估精度(P)等4项指标和χ2检验对所建立的立地指数表进行独立性检验[4]。设树高实际值为H，树高理论值为Hi。

预估精度P计算：根据29株优势解析木数据和编制的立地指数表，得出优势解析木的实测值H和理论值Hi，利用SPSS19.0软件在H与Hi之间建立一元线性回归方程，得出回归标准差、回归标准误得到模型的预测精度[4]。

3 结果与分析

3.1 导向曲线的拟合结果

日本落叶松人工林274块样地的优势木平均高—平均林龄散点图，如图1所示。根据散点图趋势，采用SPSS19.0数据处理软件的曲线回归法、非线性回归法拟合上述模型，以各数学模型的确定系数(R2)和残差平方和的平均值(EMS)作为评价各模型精度的标准，结果见表4。

图1 优势木树高—年龄原始数据分布图

各导线曲线拟合的结果如表4所示，以各数学模型的确定系数(R2)和残差平方和的平均值(EMS)作为评价各模型精度的标准[1-4]，标准为确定系数(R2)越高、残差平方和的均值EMS越小，则拟合的方程越好。从表4可以看出，确定系数(R2)较高的曲线有：单分子式、抛物线式、对数曲线式、对数双曲线式，残差平方和的均值EMS较小的曲线有：对数曲线式、对数双曲线式，综合对比后得出最佳导向曲线为：对数曲线式lg(H)=0.95lg(A)-0.05。

表4 曲线方程表达式及其计算结果统计

3.2 标准年龄和指数级距的确定

确定基准年龄是为寻找树高生长趋于稳定且能反映立地差异的年龄，本文参考基准年龄确定的依据[1]，结合本例的标准地N=274块样地数据，发现树高在18 m前变动较大，到18 a以后树高生长趋于稳定，而朗奎健等[25]于1999年撰文中国主要树种的标准年龄定为20 a，因此将树高标准年龄定为20 a。

指数级距C和指数级个数k主要根据某一地区树种在标准年龄时，树高的绝对变动幅度Δh及经营水平来确定。通常，指数级距为1～4 m，指数级个数为10个左右[1]。根据日本落叶松标准林龄(20 a)时的优势木数据：树高的变动范围为8.63～19.83 m，绝对变动幅度Δh为11.20 m，结合研究区日本落叶松生长情况，作者将指数级距定为2 m，指数级分别为8、10、12、14、16、18、20共7个。

3.3 立地指数表的编制

立地指数表的编制以导向曲线为基础，按标准年龄时的树高值和指数级距，采用标准差法、变动系数法或相对优势高法，可形成立地曲线簇(列成表即为立地指数表)。本文拟采用相对优势高法[1]，其计算公式如下：

Hij=KjHik。

式中：Hij是第i龄阶第j指数级的树高值；Kj=(Hoj/Hok)×100%为各龄阶立地指数的调整系数；Hoj为地位指数级；Hok为基准年龄时导向曲线树高；Hik为各龄阶的树高理论值。

根据上述公式计算调整系数，基准年龄20 a在拟合导线曲线对数曲线式lg(H)=0.95lg(A)-0.05中计算得出树高理论值Hok=15.345 4 m，将Hoj=8、10、12、14、16、18、20代入Kj=(Hoj/Hok)×100%得出各调整系数值Kj=0.52、0.65、0.78、0.91、1.04、1.17、1.30，并将各龄阶值代入对数曲线式方程得出各龄阶树高理论值Hik，结合公式Hij=KjHik得出各个龄阶及各指数级调整后的树高，整理后得到日本落叶松人工林的立地指数表(表5)。

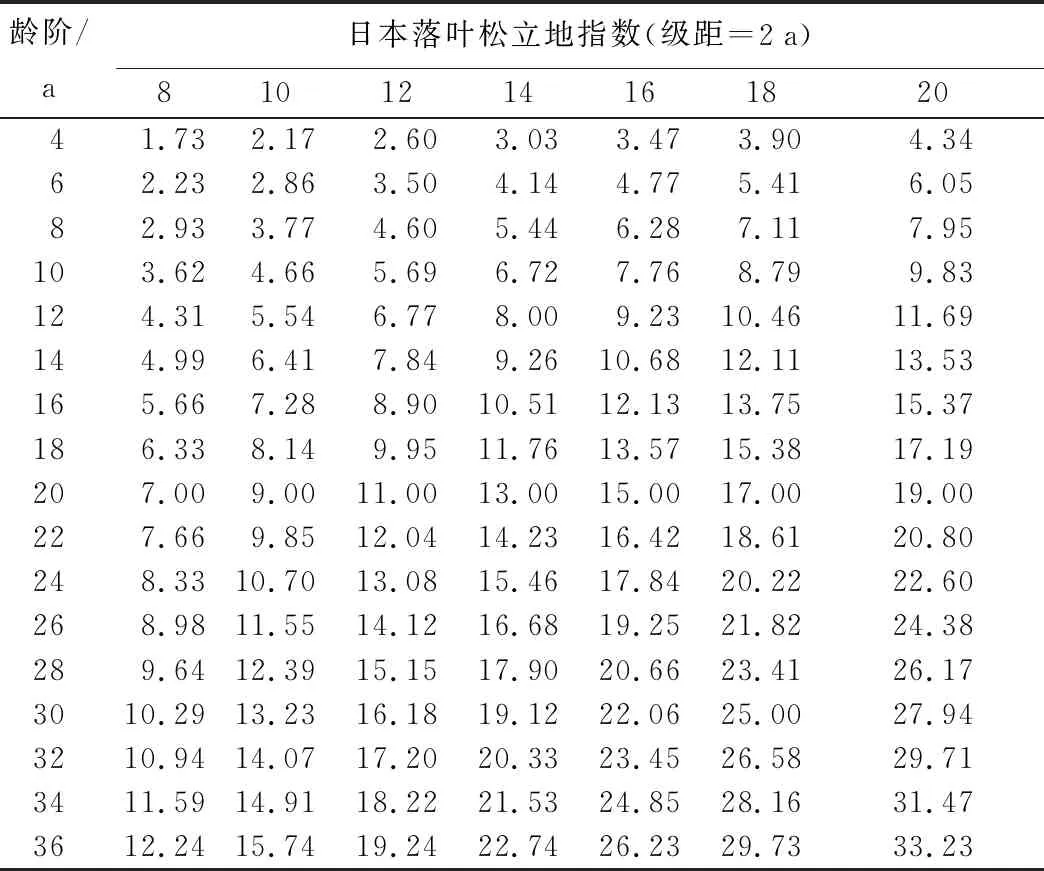
表5 日本落叶松人工林立地指数表的编制

3.4 立地指数表的适用性检验

所编立地指数表质量的高低，均体现在其适用性和预估精度上。因此，本文采用274株优势木平均高对所编立地指数表进行落点检验，采用29株优势木解析木对所编立地指数表进行适用性检验和精度检验。

3.4.1 落点检验

采用落点检验法对所编制的立地指数表进行检验(见图2)，从图2可以看出，有6个点落在立地指数曲线外，落点精度为97.7%，该精度表明所编制的立地指数表符合实际能够为实践所用。

图2 落点检验图

3.4.2 精度检验

3.4.3适用性检验——χ2(卡方)检验

4 结论与讨论

选择6个常用数学模型对亚热带地区日本落叶松人工林274块样地的优势木平均高—林龄进行导线曲线拟合，选择确定系数(R2)最优、残差平方和的均值(EMS)最小的曲线作为最优导向曲线，对数曲线式lg(H)=0.95lg(A)-0.05，确定基准林龄为20 a，指数级距为2 m，共7个指数级，运用相对优势高法导出亚热带地区日本落叶松人工林8～20 m的立地指数曲线，落点精度97.7%、预估精度98.2%，以及通过适用性检验χ2检验，均表明所编立地指数表预估精度可靠，符合实际。与马友平等[16]2001年编制的长岭岗林场日本落叶松人工林立地指数表相比，本研究在马友平的研究基础上扩大了研究区的范围(湘西、鄂西山区)、增设了研究样地、增加了解析木数据、细化了研究区立地因子，更能充分反应日本落叶松生长情况，更好的为实际生产服务。

近年来全球极端天气频发，在气候变化的大背景下，湘西、鄂西地区近年多次发生冰冻灾害等自然干扰，此类自然干扰均有可能对日本落叶松树高生长造成影响。如，2008年湖南地区因冰冻天气使森林资源遭到破坏[14]，导致调查的样本中14、30 a的日本落叶松优势木的数据只有2株，而且林龄主要集中于6、8、20 a，且亚热带地区日本落叶松人工林以幼龄林、中龄林、近熟林为主，成熟林、过熟林较少。在后期持续的研究中，可逐渐增加成熟林数据，以提高立地指数表精度。国际上有研究学者加入气象因素，提高树种立地指数表的适用性及精度[26]，为精进日本落叶松立地指数表，后期研究可加入气象因素[27]，以对亚热带地区日本落叶松的立地质量进行更科学的评价，对日本落叶松的生长提供更全面的科学依据。