应用高斯聚类的单木分割及树高和冠幅的提取1)

张怡卓 吕阿康 蒋大鹏 陈金浩 王克奇

(东北林业大学，哈尔滨，150040)

树高和冠幅不仅是反映林分结构特征的重要指标，而且在生产潜力预估、生物量预测、林木生长预测等研究中也是最常用的观测变量。因此，单木分割及树高冠幅提取在森林资源调查中具有重要的意义。机载激光雷达作为一种主动遥感技术，具有较强的穿透能力，并不易受天气及光照条件影响，可获得高精度的地表及地物的垂直结构信息。运用机载激光雷达技术，可有效提取单木及树高冠幅等参数信息[1-2]。

目前，单木分割与树高冠幅提取方法可分为两类：基于栅格化的冠层高度模型(CHM)和基于点云聚类的分割方法。其中，基于栅格化的CHM-分割方法是通过确定树冠边界或局部最大值识别树冠顶点，采用区域生长或图像分割技术进行单木分割与结构参数提取。王轶夫等[3]在CHM上采用固定窗口识别树顶点提取林木树高，提取的样地平均树高与实测值线性回归关系系数为0.694，固定窗口大小直接决定识别局部最大值的结果。李响等[4]、甄贞等[5]利用动态窗口局部最大值法对单木位置进行探测，采用标记控制区域生长法进行冠幅勾绘的树冠面积相对误差平均值为8.74%，由于树木生长呈阶段性变化，方法应用具有一定局限性。耿林等[6]针对CHM表面存在的孔洞问题，采用线性平滑方法使树冠边缘连续，树冠内部得到填充，并利用局部动态窗口探测树冠顶点进而提取树高，但是冠层表面平滑程度难以控制，导致单木结构参数提取精度不高。基于点云聚类的分割方法，采用聚类算法直接对原始点云进行单木分割与树高冠幅提取，消除了栅格化CHM丢失数据的现象。Sandeep et al.[7]采用K-means聚类法实现对原始激光雷达点云数据的单木分割，但单木参数提取结果依赖于初始值的选取。Ferraz et al.[8]提出基于均值偏移算法的聚类方法实现单木分割，该算法不需要选择聚类的数量，但因森林环境复杂，树木大小不均匀，均值滑动窗口大小难以确定。Li et al.[9]将全局最大值点作为最高树的顶点，根据点云空间距离判别进行聚类，在单木树高提取方面达到较好效果，但未能准确勾画出树木冠层部分。Lu et al.[10]根据点云的强度和回波特征分离树干，将点识别为树木点和噪声点，但该算法需要更加密集的点云数据，数据采集成本高。赵晨阳等[11]在确定聚类数量基础上，以树冠顶点为聚类中心，经过迭代后估测单木冠幅的相关性系数为0.76，冠幅分割稳定性较差。Ayrey et al.[12]提出基于原始点云的分层叠加聚类方法，该方法对整个森林点云进行高度间隔切片，并对每一层进行聚类实现树冠形状的三维重建，但方法依赖聚类条件。

基于栅格化的冠层高度模型(CHM)的单木分割及树高冠幅提取方法易造成点云丢失，且树冠部分不完整导致噪声点出现；而利用原始三维点云进行单木分割及树高冠幅提取避免点云信息丢失，但分割结果需以单木数量为已知搜索条件，故该方法存在局限性。本研究以针叶材为研究对象，利用机载激光雷达获取点云数据，提出一种基于高斯模型聚类的单木分割及树高和冠幅的提取方法，根据单木形状结构建立高斯模型，通过确定单木位置及初步树冠范围，利用高斯轮廓约束聚类得到树高和冠幅的精准提取。

1 研究区概况

研究区位于美国华盛顿州国会森林蓝岭地区，该区域地貌主要以丘陵为主，海拔260～425m，地面坡度0°～45°。研究区域内以针叶林为主，森林植被树种主要为道格拉斯冷杉(Pseudotsugamenziesii)、西部铁杉(Tsugaheterophylla)和西部红雪松(Thujaplicata)。根据华盛顿州自然资源部和华盛顿大学对蓝岭地区347个野外调查点进行地形调查实测单木结构参数的基本统计量见表1。

表1 实测单木结构参数的基本统计量

本研究数据采集时间为1999年春季，采用Saab TopEye LiDAR系统获取小光斑机载雷达点云数据。遥感平台飞行高度为200 m，飞行倾角为8°，采样密度4次/m2脉冲回波，激光脉冲速度7 000点/s，最大回波记录为4次，光斑直径为40 cm，直升机飞行速度为25 m/s，扫描宽度70 m。实验选取6块半径30 m的圆形纯林样地(实测单木共893株)，样地面积共1.69 hm2，平均点密度约为4.86点/m2，标记为Plot1、Plot2、Plot3、Plot4、Plot5、Plot6(样地位置如图1所示)。该研究区彩色航空影像以蓝岭地区通过自相关技术衍生的伪树冠表面模型利用软考贝摄影测量系统完成正摄校正，最终图像分辨率为0.3 m。

2 研究方法

2.1 研究路线

高斯模型聚类的单木分割及其参数提取方法技术路线如图2所示。针对区域LiDAR点云数据，使用Kriging插值法生成冠层高度模型(CHM)，通过形态学开运算和高斯滤波得到GCMM模型；利用局部最大值法和最速下降法的高斯曲面拟合得到单木位置及初步冠幅范围；将归一化点云数据采用最小二维欧式距离聚类得到三维单木及树高；最后，利用实测数据分别对提取的冠幅和树高进行精度验证和分析。

图1 研究区彩色航空影像

2.2 三维单木分割方法

2.2.1 局部最大值点探测

首先将原始点云分为非地面点和地面点[13]，分别进行插值运算[14-18]，得到数字地面模型(DSM)和数字高程模型(DEM)，两者作差值运算求得CHM[19]；由于原始的CHM中存在黑色或灰色的孔洞，进而影响树顶点的探测。对CHM模型表面进行形态学开运算，将CHM模型中的孔洞替换为邻域内点云高度最大值点，形成冠层最大模型(CMM)模型，即

(1)

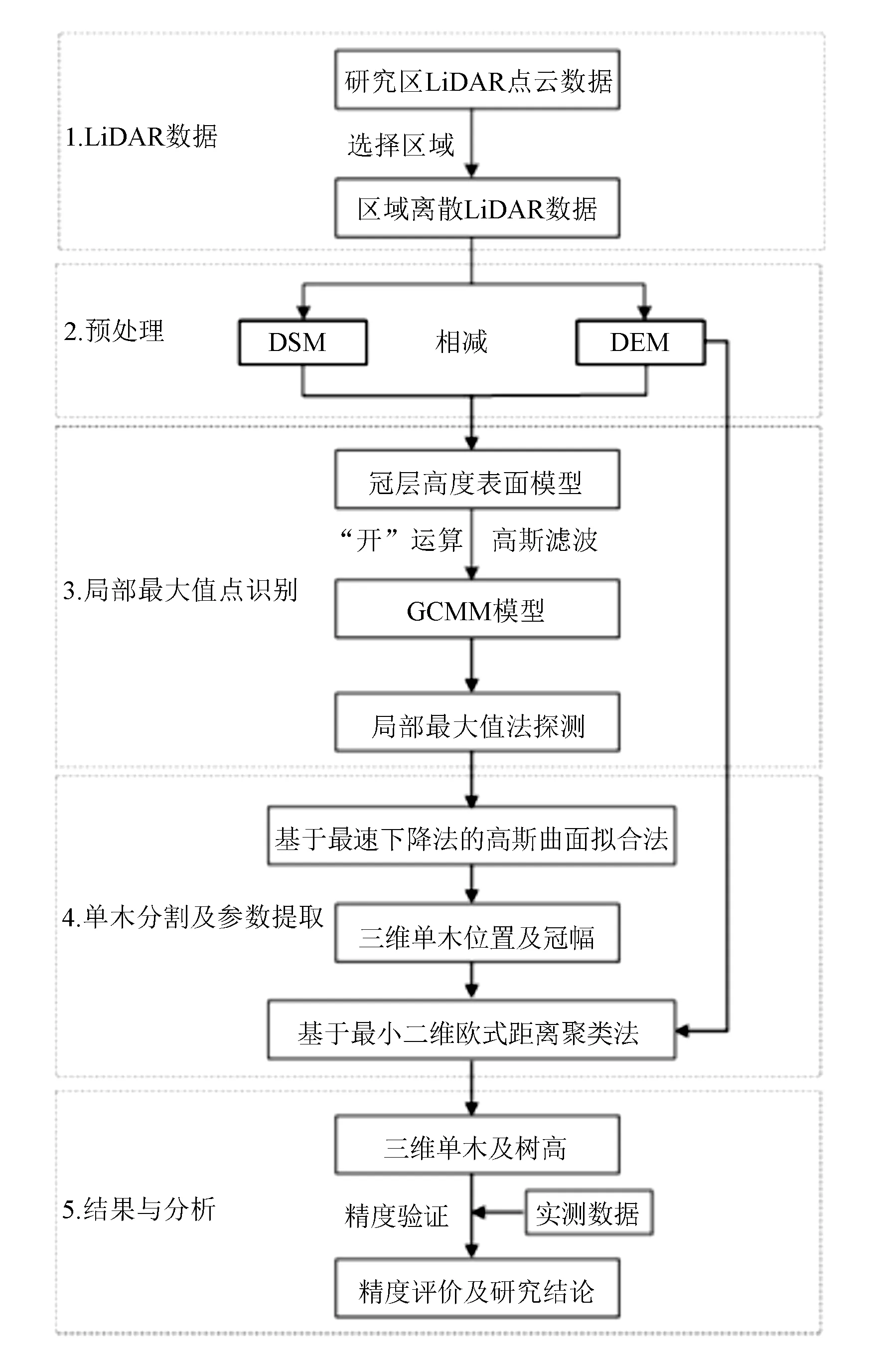
图2 高斯模型聚类的单木分割及其参数提取方法技术路线

CMM模型可增强树冠边缘信息使树冠表面更平滑，运用高斯滤波方法对CMM模型进行线性平滑处理得到GCMM模型，即

G=G5×5×C。

(2)

式中：G为GCMM模型；C为CMM模型；G5×5为5×5(像元)的高斯矩阵。

固定窗口能准确地识别树顶点，通过实验分析选用大小5×5(像元)窗口可以找到GCMM模型局部最大值点，使用GCMM模型可消除伪局部最大值，减少树梢识别中错误检测。

2.2.2 最速下降法的高斯曲面拟合

通过GCMM模型的栅格点进行高斯曲面拟合，该模型灰度图像矩阵为EM×N(1≤i≤M,1≤j≤N)，在三维空间中当x=i，y=j时z=eij，z代表图像的灰度值大小，且满足条件eij>0，其高斯曲面模型表达式为

(3)

化简式(3)可得

(4)

令B=lnA，则式(4)可改写为

(5)

则上述问题转化为求参数B、x0、y0、a(参数B、x0、y0、a都是1×n的数组)，使得目标函数为

(7)

实验采用最速下降法的算法计算X=(B，x0，y0，a)T的流程如下。

①给定初始值X0，ε>0，k=0计算

F0=F(X0),g0=g(X0)=F(X0)。

(8)

式中：g(x)=(g1、g2、g3、g4)T。

②计算

(9)

Xk+1=Xk-tkg(Xk)；

(10)

Fk+1=F(Xk+1),gk+1=g(Xk+1)。

(11)

式中：H(X)=2F(X)=(hij)(4×4)。

运用最速下降法求解出拟合后的混合高斯模型为

(12)

式中：(xn，yn)为混合高斯曲面拟合后的单木位置；An为(xn，yn)所在位置的灰度值大小；an为混合高斯曲面拟合后的树冠范围。

2.2.3 基于最小二维欧式距离聚类

基于混合高斯模型的最小二维欧式距离聚类是将高程归一化点云进行距离迭代判断，划分临近点云归属情况，实现三维单木准确分割。其利用最小二维欧式距离聚类算法如下：

①定义(xn，yn)所在空间位置为簇的中心线，提取样本与中心线距离小于或等于4an的点云集群；

③重复步骤②，直到所有样本点被划分至相应簇时停止，实现单木三维分割。

2.3 精度评价方法

本研究从二个方面对机载雷达点云提取单木及树高冠幅能力进行评价，通过实测地面数据和高空间分辨率图片进行目视解译得到单木分割精度的验证，具体方法如下。

①采用召回率r、正确率p、调和值F3个指标衡量单木分割精度。

r=TP/(TP+FN)；

(13)

P=TP/(TP+FP)；

(14)

F=2×(r×p)/(r+p)。

(15)

式中：TP为正确分割树分割精度；FN为欠分割树分割精度；FP为过分割树分割精度。

②对正确分割的三维单木进行树高冠幅精度评价和线性回归分析[20]，其精度评价计算公式为

(16)

式中：n为正确分割的三维单木数量；Mi为分割单木结构参数；Ni为实测单木结构参数。

3 结果与分析

3.1 三维单木分割结果

在6块样地中选取半径为10 m的圆形样地，圆形样地共有实测树木12株，基于两种模型树冠顶点识别结果如图3所示。基于局部最大值法检测树冠顶点时，采用GCMM模型可消除12个伪局部最大值，且树冠顶点识别未受到影响。

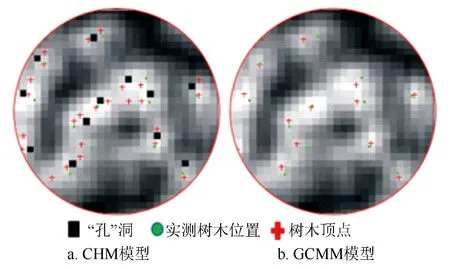
图3 树冠顶点识别结果

采用不同大小窗口分别对6块样地的GCMM模型进行局部最大值探测找到初步的树冠顶点。6块样地实际单木为893株，相比实际单木值3×3(像元)窗口共检测到1 153个树冠顶点，多检测到260个树冠顶点，而7×7(像元)窗口共检测到537个树冠顶点，存在未识别树冠顶点356个，因此实验选用5×5(像元)窗口找到GCMM模型中局部最大值点。

采用高斯模型聚类法和分水岭方法分别对6块样地点云进行单木分割，其分割结果如图4所示。Plot5和Plot6样地点云密度高，树木数量较多，运用分水岭方法进行单木分割存在严重的过分割现象，并且提取到树冠闭合边缘存在残缺现象。由于针叶冠层俯视形似圆形，单木点云在GCMM模型中符合高斯分布，高斯模型聚类法初步提取到的树冠范围更加接近真实树木形态。高斯模型聚类方法利用局部最大值法在GCMM模型上探测初步树木位置，减少了单木过分割数量。通过与实测树木位置(图4中绿色圆点位置)进行比对可知，该方法分割准确性更高。

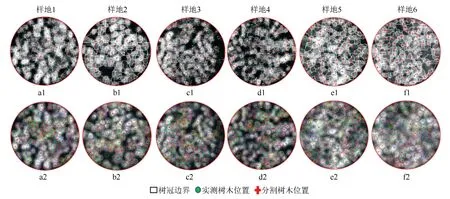
a1、b1、c1、d1、e1、f1为分水岭算法；a2、b2、c2、d2、e2、f2为高斯模型聚类法。

如表2所示，6块样地共有893株，高斯模型聚类方法分割了860株，其中正确分割790株，过分割103株，欠分割70株。基于分水岭方法分割了867株，该算法正确分割为709株，过分割184株，欠分割158株。与分水岭方法相比，高斯模型聚类法是基于GCMM模型的局部最大值检测进行单木分割，提高了11.3%准确率。

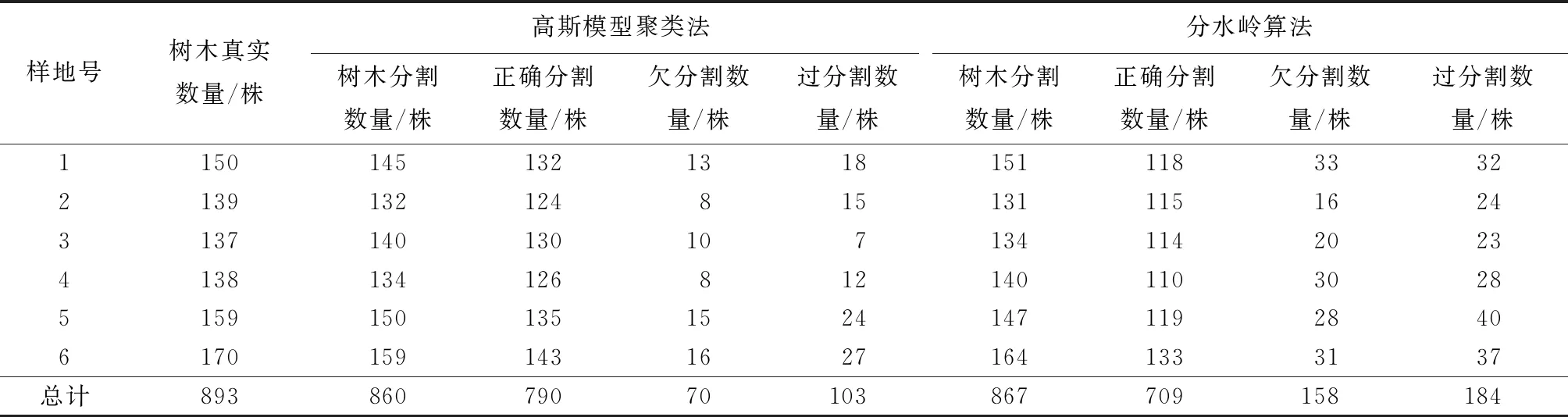
表2 高斯模型聚类法和分水岭算法准确性评估

如表3所示，分水岭算法平均调和值仅为0.80，是基于CHM模型参考空间位置和灰度值相近的像素点互相连接起来构成一个封闭轮廓，形成单木冠层易导致过分割现象。而高斯模型聚类法是基于GCMM模型采用局部最大值法探测得到树冠顶点，在树冠顶点处使用最速下降法的高斯曲面拟合，最大程度拟合树木真实形态，保证单木分割准确性；但由于plot5和plot6林分郁闭度较高，激光信号无法识别林下较小树木，平均F值为0.89。相比于分水岭算法，高斯模型聚类法在6块样地分别得到r平均值为0.87，p平均值为0.91，证明该方法的优越性。

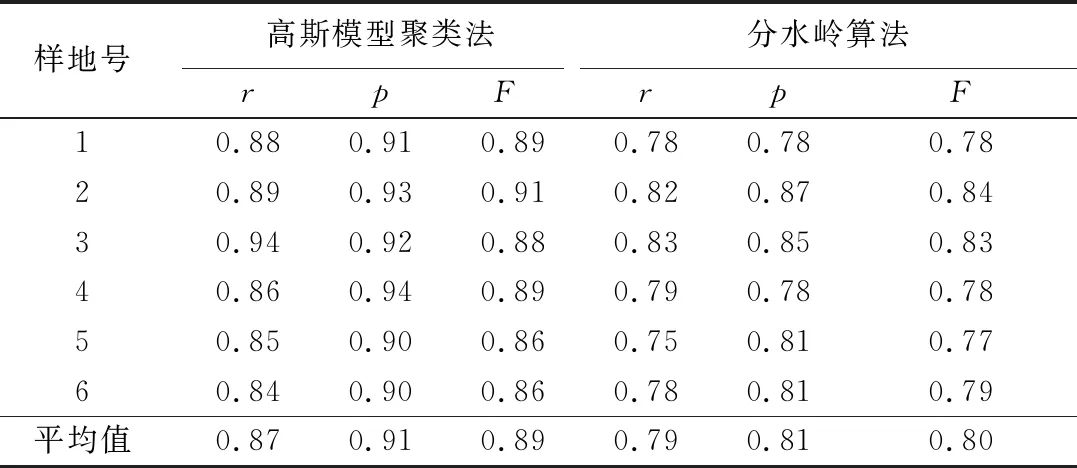
表3 两种方法分割精度得分

3.2 单木树高和冠幅参数提取结果

使用高斯模型聚类方法和分水岭方法对6块样地进行单木树高和冠幅提取，树高提取精度分别为95%和90%，冠幅提取精度分别为91%和86%。两种方法正确分割三维单木提取的冠幅与实测冠幅的线性回归关系如图5c、图5d所示，高斯模型聚类方法R2=0.84，但分水岭方法冠幅提取结果较弱，R2=0.73；单木树高的线性回归关系如图5a、图5b所示，分水岭方法R2=0.84，相比于该方法高斯模型聚类方法树高提取结果较好,R2=0.92。

从实验结果得出，高斯模型聚类法和分水岭法树高提取的平均误差分别为-0.83、-1.41 m，平均误差为负值，表明树高存在低估现象，可能是由于激光点采样密度不够大，导致系统无法获取全部树木信息。利用两种算法提取冠幅的平均误差分别为-0.42、1.05 m，分析发现：本研究样地树木为针叶类型，树冠俯视形状近似圆形，高斯曲面拟合法比分水岭算法提取到树冠更接近真实情况，冠幅提取平均误差减小0.63 m；相比于分水岭方法，高斯模型聚类法直接对原始点云进行聚类，避免了CHM模型采用栅格内最大值法导致树木信息丢失，保证点云信息完整性，提取树高平均误差减少0.58 m。

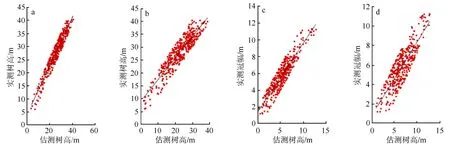
a.高斯模型聚类法树高；b.分水岭算法树高；c.高斯模型聚类法冠幅；d.分水岭算法冠幅。

4 结束语

高斯模型聚类算法性能良好，相比于分水岭算法单木分割召回率r为0.87，正确率p为0.91，综合r和p的调和值F为0.89，该算法提取冠幅与树高精度分别为95%，91%，平均误差分别为-0.42、-0.83 m，表明该算法具有良好的应用前景。

现阶段的单木分割及树高冠幅的提取研究中，针叶纯林仍占据重要地位，由于针叶林形状大多为中心高，四周低的伞状，分布较为规则，易在遥感影像中辨认。在今后研究中基于高斯模型聚类方法可尝试加入更多有效的约束规则来提取复杂阔叶林或针阔混交林的森林结构参数，如生物量[21]、叶面积指数和蓄积量等。