异形现浇无梁板桥有限元受力分析

徐伟博

（天津市市政工程设计研究院，天津300392）

无梁板桥于构造上有较强的适应性，其上部可以适应城市复杂情况的弯、斜和特殊异形板，下部墩柱也可以根据实际情况布置，以满足排水要求和形成净空[1]。

随着经济的发展，近年来，国内各地大量修建城市立交与高速公路，无梁板桥由于较强的适应性，也被更多的采用，主要有三种类型：

1）简支斜板桥；

2）整体式连续斜交板桥；

3）整体式不规则异形板。

第一、二种类型结构相对简单，对此研究较多[2～4]；而对复杂路线情况下的第三种类型结构研究较少。

本文采用三维有限元模型计算方法，对比分析某大异形整体式现浇无梁板桥的内力变化特点。

1 工程概况

某主路与河道斜交角度约35°，河道斜长约280 m，跨河主桥采用非对称独塔斜拉桥结构，两侧接斜交地下通道。

由于项目为大跨径，跨河主桥两侧接大角度斜交地道，为解决结构构造和受力问题，引桥采用现浇实心板梁，现浇板梁与墩柱采用支座连接，以释放由于边长不同产生的较大温度纵向力。板梁靠近主桥侧搭在主桥边墩的牛腿上，采用滑板支座，每隔2 m布置一个，斜边每隔6 m布置一个，板桥跨中支承采用滑板支座，斜向布置6个桥墩。见图1和图2。

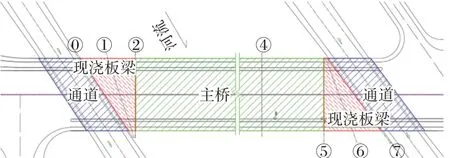
图1 工程平面布置

图2 无梁板桥平面

2 模型的建立

对不规则异形板结构，采用数值法求得精确解析解是不可能的，因而采用Midas板单元建模，将这些单元划分为四边形，在节点上相互连结，从而更为准确地模拟结构受力性能。见图3。

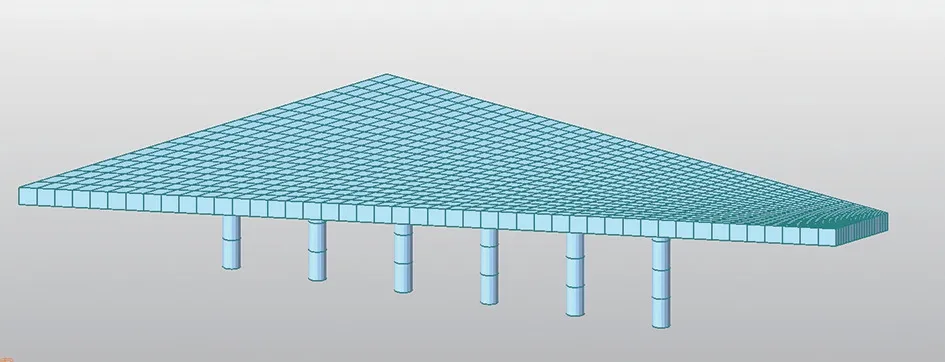
图3 整体模型及单元划分

梯形板的长边为36 m，短边5 m，直角边46 m，板厚1.2 m。

全桥均布恒载为24 kN/m2；汽车荷载等级为城-A级；桥面采用双向8车道布置，桥面宽度2×15.25 m(行车道)+2×2 m(隔离带)+2×3.5 m(非机动车道)+2×2.25 m(人行道)。

3 计算结果分析

主要通过三方面对结构进行分析：

1）本结构为双向板，故首先分析顺桥向与横桥向内力结果；

2）分别考虑恒载、活载、支座沉降与温度作用产生的结构内力，分析结构的受力特点；

3）对比分析是否考虑支座、墩底刚度情况下，对结构支反力与内力的影响。

3.1 承载能力极限状态下弯矩计算

顺桥向（x轴方向）选取承载能力极限状态下的单位宽度弯矩，见图4和图5。

图4 顺桥向单位宽度弯矩

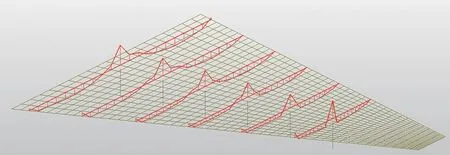
图5 顺桥向单位宽度弯矩剖断面

由图4和图5可知，顺桥向弯矩结果同两跨连续梁桥基本一致，单位宽度最小弯矩为-2 397 kN·m/m，位于1#墩墩顶位置处；单位宽度最大弯矩为1 091 kN·m/m，位于2#墩与直角边中间位置附近。

横桥向（y轴方向）选取承载能力极限状态下的单位宽度弯矩，见图6和图7。

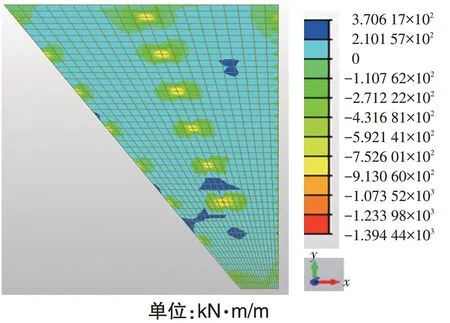
图6 横桥向单位宽度弯矩

图7 横桥向单位宽度弯矩剖断面

由图6 和图7 可知，横桥向板体大部分范围承受正弯矩，负弯矩主要出现在中墩顶附近区域、直角边斜边两侧支座顶部区域、钝角至直角边区域。单位宽度最大弯矩为371 kN·m/m，位于6#墩至短边中间附近；单位宽度最小弯矩为-1 394 kN·m/m，位于6#墩墩顶位置处。

综上，结构承载力顺横向均受中墩顶部负弯矩控制：顺桥向为最大跨径处墩顶负弯矩控制，横桥向为靠近钝角边墩顶负弯矩控制。

3.2 各分项作用结果对比

分别提取恒载、活载、支座沉降（2.5 mm）作用下中墩墩底反力，见表1。

表1 各作用下中墩墩底反力kN

由表1可知，恒载作用下，①～⑤墩支反力逐渐减小，表明支反力主要受跨径的影响，⑥号墩由于承受钝角边较大恒载，故反力也较大；沉降作用下，支反力分布不均匀，⑥号墩到小直角边由于缺少均匀支撑，故反力远大于其他墩位反力。

3.3 支座和墩底刚度对板梁内力的影响

通过有限元模型，分别计算不考虑支座、墩底刚度与考虑支座、墩底刚度条件下，结构支反力与内力，对比分析刚度条件对结构内力的影响。

支座刚度按照实际支座模拟，刚度取SDx=SDy=3 200（kN/m）；墩底刚度按照桩基础对上部结构的支撑作用采用6×6的刚度矩阵模拟，刚度值用m法计算，根据地勘报告，m值取8 000 kN/m4。

承载能力极限作用下，斜边、中墩、直角边最大、最小支反力见表2。

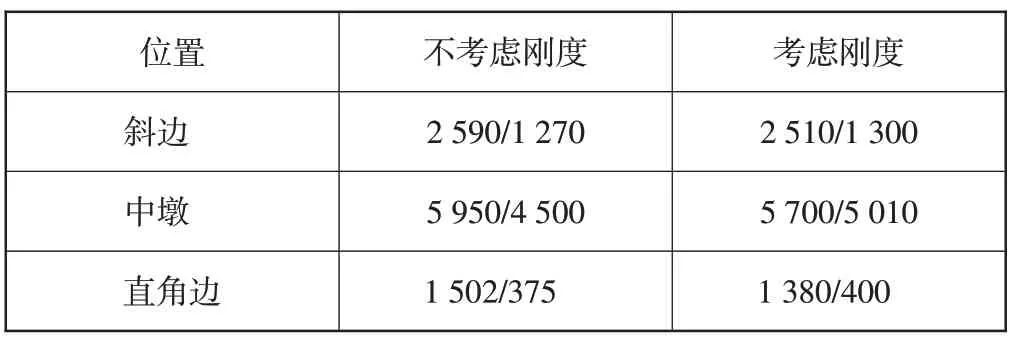
表2 斜边、中墩、直角边最大/最小支反力kN

由表2 可知，承载能力极限作用下，是否考虑支座、墩底刚度各支座支反力变化趋势相同，考虑刚度情况下各支座最大支反力小3%～10%，最小支反力大2%～11%，其中中墩位置变化更加明显。

承载能力极限作用下，板梁单位宽度最大/最小弯矩见表3。

表3 单位宽度最大/最小弯矩kN·m

由表3 可知，承载能力极限作用下，是否考虑支座、墩底刚度顺桥向、横桥向单位宽度弯矩变化趋势一致，最大弯矩减小2%～6%，最小弯矩增大14%～18%。

综上，考虑支座、墩底刚度的条件下，支反力与单位宽度弯矩变化趋势相同，其数值均更加平均，表明考虑支座、墩底刚度对板梁受力是有利的。

4 结论

1）异形板梁结构应考虑顺、横桥向双向受力，连续结构中受力特点与普通连续结构桥梁基本一致，受墩顶负弯矩与跨中正弯矩控制。另外，应特别注意钝角位置处结构的内力集中情况。

2）异形板的墩柱位置布置是影响其受力的重要因素，设计中应充分考虑结构受力的均匀性，可通过有限元模型分析，确定墩柱的合理布置位置。

3）模型分析中可考虑支座、墩底刚度对异形板结构的有利作用，从而优化结构配筋。□■