严格α2-对角占优M-矩阵线性互补问题误差界的新估计
周平
(文山学院 数学与工程学院,云南 文山,663099)
线性互补问题是在对策论、弹性力学、经济学、市场营销、数学规划等领域具有广泛应用的一类优化问题[1],通常它的模型是指求x∈Rn,满足:
Ax+q≥0,(Ax+q)Tx=0,x≥0,
简记为LCP(A,q),此处,A=(aij)∈Rn×n表示n阶实矩阵,q∈Rn表示n维实向量。
在LCP(A,q)的一些实际应用中,常常要对它的解进行误差分析。从它的模型可以发现,LCP(A,q)的解的性质主要取决于矩阵A的结构和性质,当A为P-矩阵时,线性互补问题的解存在且唯一[2]。CHEN等[3]给出了相应的误差界:
其中:r(x)=min{x,Ax+q};x*表示LCP(A,q)的解;D=diag(d),d=(di)∈Rn,0≤di≤1,i=1,2,…,n。现有一些研究者对此问题中矩阵A具有某些特殊结构,如:B-矩阵、S-Nekrasov矩阵、B-S-Nekrasov矩阵、S-QN-矩阵或弱链对角占优矩阵等进行了深入研究,获得了相应误差界的一系列颇有成效的估计式[4-9]。而对于严格α2-对角占优M-矩阵的情形,文献[8]给出如下结果:
(1)
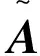
向爱[9]获得如下估计式:
(2)

文章继续讨论了LCP(A,q)中A是严格α2-对角占优M-矩阵时的误差界问题,给出了其相应的一个新估计式,通过数值例子表明了新结果的优越性。
1 符号、定义和引理
为了便于探讨,先给出如下记号。
记N={1,2,…,n},Rn×n是全体n×n阶实矩阵构成的集合。设A=(aij)∈Rn×n,对任意的i,j,k∈N,j≠i,令
定义1[1]设A=(aij)∈Rn×n且aij≤0,i≠j;i,j∈N,则称A为Z-矩阵;如果A为Z-矩阵且A-1≥0,则称A为M-矩阵;若
则称A为严格对角占优(SDD)矩阵。
定义2[2]设A=(aij)∈Rn×n,如果A的所有元素aij≥0,那么A叫做非负矩阵,记为A≥0。

引理1[10]设A=(aij)∈Rn×n为严格对角占优M-矩阵,则

引理2[4]若γ>0,η≥0,则对任意的x∈[0,1],有

引理4[5]设A,B∈Rn×n,A和A-B非奇异,则有
(A-B)-1=A-1+A-1B(I-A-1B)-1A-1。
引理5[6]设A=(aij)∈Rn×n,如果‖A‖<1,那么I-A非奇异,并且
2 主要结果
应用第一部分给出的引理,结合不等式的放缩技巧和矩阵分裂的技术,给出严格α2-对角占优M-矩阵线性互补问题解的误差界的新估计式。

其中:

证明令矩阵A=B-F,这里B=(bij)∈Rn×n是SDD矩阵,F=diag(fij)∈Rn×n且是
非负的,其中,
由于A为严格α2-对角占优M-矩阵,所以有
当i∈N1时,
当i∉N1时,
从而由定义1可知:矩阵B是严格对角占优M-矩阵。设G=I-D+DA,则
G=I-D+D(B-F)=(I-D+DB)-DF,D=diag(di),0≤di≤1,i=1,2,…,n。
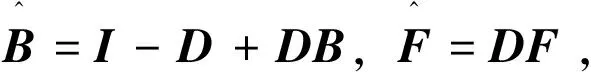
对任意的i,j,k∈N且j≠i,根据引理2和引理3,可知:
(3)
(4)
(5)
由式(3)~(5),得
进而根据引理4和引理5,可知:
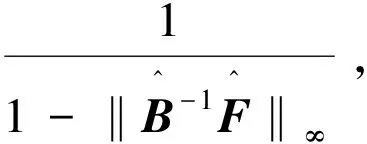
进一步有
故综上,得
下面对定理1和文献[9]中的定理进行比较。
定理2 设A=(aij)∈Rn×n是严格α2-对角占优M-矩阵,α∈[0,1],若
N1={i∈N:Ri(A)>Ci(A)}≠Ø
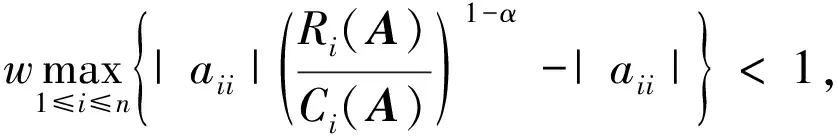
其中:w的定义与式(2)相同,μ的定义与定理1中的相同。
证明由文献[10]中的定理,可知:
又根据文献[11]中的定理可知:
另外,由uj和lj的定义,可知:
0≤uj(A),lj(A)<1
从而,有μ≤w,故该定理成立。

