基于多目标粒子群算法的分布式电源优化配置研究

唐杰，唐婷婷，陈日恒，李智珍，邓琪伟，姜有华

(多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳,422000)

分布式电源(distributed generation，DG)与传统供电模式完全不同，分布式电源具有低污染性、安装灵活方便等优点，能够有效缓解能源枯竭、环境污染问题[1]。随着分布式电源容量的增加，给配电网带来网络损耗增加、线路潮流倒流、短路电流增大、电能质量受损等不良影响，同时也增大了配电网规划的不确定性[2-3]，这类不良影响和不确定性与分布式电源在配电网中的优化配置有密切关系。因此，科学合理地确定分布式电源的接入位置和容量，对配电网经济、安全和稳定有效地运行具有重要意义。

目前，国内外许多学者对分布式电源的优化配置问题提出了不同的解决方案。对分布式电源接入的位置及容量的求解算法大致可分为经典的数学规划方法和现代智能优化算法[4]。文献[5]考虑到分布式电源的建设运行成本及网络损耗，提出了一种改进萤火虫算法和天牛须算法的混合算法，并建立数学模型，通过IEEE33节点仿真验证模型的合理性及方法的正确性；文献[6]引进罚函数，将非线性的约束条件转化为一系列无约束问题，提升了算法的运行效率与收敛速度。文献[7]提出了一种改进的自适应权重粒子群算法，对粒子的全局搜索能力与局部搜索能力进行了均衡；文献[8]将人工蜂群算法的搜索系数与混合蛙跳算法的个体位置更新思想融入标准粒子群算法中，解决了粒子群算法容易陷入局部最优及收敛速度慢的缺陷，提升了粒子群算法的运算速度；文献[9]结合了共享学习因子与动态拥挤距离策略，采用动态的拥挤距离策略维护外部粒子的搜索范围，加强了算法的搜索能力。

本文针对分布式电源安装位置和容量的配置问题，以投资运行总成本最小、有功网损最小和节点电压偏差最小为目标函数，在考虑功率平衡、节点电压功率、线路传输功率和节点安装容量等约束条件下，采用自适应权重更新策略的多目标粒子群算法对所建立模型进行求解分析，得到的Pareto非劣解集更能接近最优解。通过IEEE33节点进行仿真验证，能够有效地降低投资运行成本及网络损耗，证明了所建立模型和算法的正确性和有效性。

1 分布式电源优化配置的数学建模

本文建立了以分布式电源投资总成本最小、配电网的总有功损最小和节点电压偏差最小为目标函数，以功率平衡、节点电压功率、线路传输功率和安装容量为约束配电网节点的约束条件来搭建数学模型。

1.1 目标函数

1.1.1 分布式电源投资运行总成本

分布式电源投资运行成本表达式为

(1)

式中:t为计划使用年限的第t年；r为年利率；xi为0～1间随机变量，表现为节点i处是否接入分布式电源；N1为分布式电源的安装节点数目；N2为分布式电源的规划运行年限;Pi为节点i处分布式电源的安装容量；AC为分布式电源的单位购置成本；CC为单位基础建设成本；IC为单位安装成本；LC为单位土地使用成本。

1.1.2 配电网总有功网损

配电网的总有功网损用牛顿-拉夫逊计算网损公式表示为[7]

(2)

(3)

(4)

式中:N为总节点数目；Rij和Xij分别为线路ij之间的电阻和电抗；P和Q分别为流入节点的有功和无功功率；V为节点的电压幅值；θ为节点电压相角。

分布式电源接入配电网后，节点i处的负荷需求表达式如下所示：

Pi=PDGi-PDi

(5)

Qi=QDGi-QDi

(6)

综合上面公式可得，含有分布式电源系统的有功网损计算公式为

(7)

1.1.3 节点电压偏差

节点电压偏差表达式为

(8)

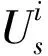
1.2 约束条件

1.2.1 功率平衡约束

功率平衡约束公式见式(9)和(10)。

(9)

(10)

式中：R为节点i与节点j相联通所形成的集合；Pi为i节点处流入的有功功率；Qi为流入的无功功率；Ui为节点电压幅值；Gij为节点ij之间的电导；Bij为电纳；θij为电压向角差。

1.2.2 节点电压约束

Uimin≤Ui≤Uimax

(11)

式中：Uimax和Uimin分别为节点i处电压的最大值与最小值。

1.2.3 安装容量约束

在配电系统中，所有节点安装容量的总和不能超过DG占系统总负荷容量最大值。

(12)

式中：Pi为第i个节点的有功容量；η为分布式电源占总负荷容量的最大值；P为总的负荷容量。

1.2.4 线路传输功率

(13)

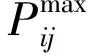
2 基于粒子群算法的多目标优化方法

针对分布式电源优化配置问题，将自适应权重更新策略的粒子群算法应用于所建立的三目标优化模型进行求解分析，能够更好地约束粒子的飞行速度与更快地找到最优解。

2.1 多目标粒子群算法

多目标粒子群算法能够有效解决单目标问题的单一性，在搜索最优解的原理上加入了一种非支配排序思想，能够更有效地提升求解速度和目标精度。在解决实际问题上，通常从2个方面进行改进：一种是改变粒子拓扑关系结构，另一种则是优化种群排序。文中采用自适应惯性权重对粒子进行更新，比线性变化的速度惯性权重因子能更好地对粒子进行更新约束，其迭代公式见式(14)和(15)：

vi+1=ω×vi+c1×r×(pbesti-xi)+c2×r×(gbesti-xi)

(14)

(15)

式中：c1和c2为学习因子，c1=2.5+(0.5-2.5)×t/g，c2=0.5+(2.5-0.5)×t/g，t为粒子当前迭代次数，g为粒子总迭代次数；r为0～1之间的随机数，pbesti为粒子最优位置，gbesti为群体的全局最优位置，xi为粒子的当前位置；ωmax和ωmin为惯性权重的最值；f为粒子的适应度值；favg为粒子群适应度均值；fmin为适应度最小值。自适应权重的粒子群算法对于粒子速度的更新在于赋予适应度大于或小于平均适应度不同的权重，从而能够更好地约束粒子的飞行速度及位置。

2.2 求解步骤

采用自适应更新策略的粒子群算法对建立的多目标数学模型进行求解，具体算法流程见图1。

图1 自适应更新权重的粒子群算法流程图

3 算例仿真分析

为了验证文中所建立模型和算法的正确性和可行性，采用IEEE33节点进行仿真分析。

3.1 算例主要参数

采用IEEE33节点配电网测试系统作为测试对象，结构图见图2。IEEE33节点测试系统的基本负荷为3 715 kW+j2 265 Kvar，基准电压为13.66 kV。

图2 IEEE33节点配电网测试系统

粒子群算法的基本参数设置见表1。

表1 算法的基础参数

3.2 仿真结果分析

在Matlab2014a环境下运行得到的Pareto前沿面见图3。从图3可以看出，本文算法求解得到的Pareto解集分布较均匀，且最优解的位置较为均匀分布在一条直线附近。从图4可以看出，与标准粒子群相比较，采用自适应更新权重的粒子群算法能更快速地从局部最优解中跳出来，从而寻找到更优的解，在计算过程中，粒子收敛速度较快。

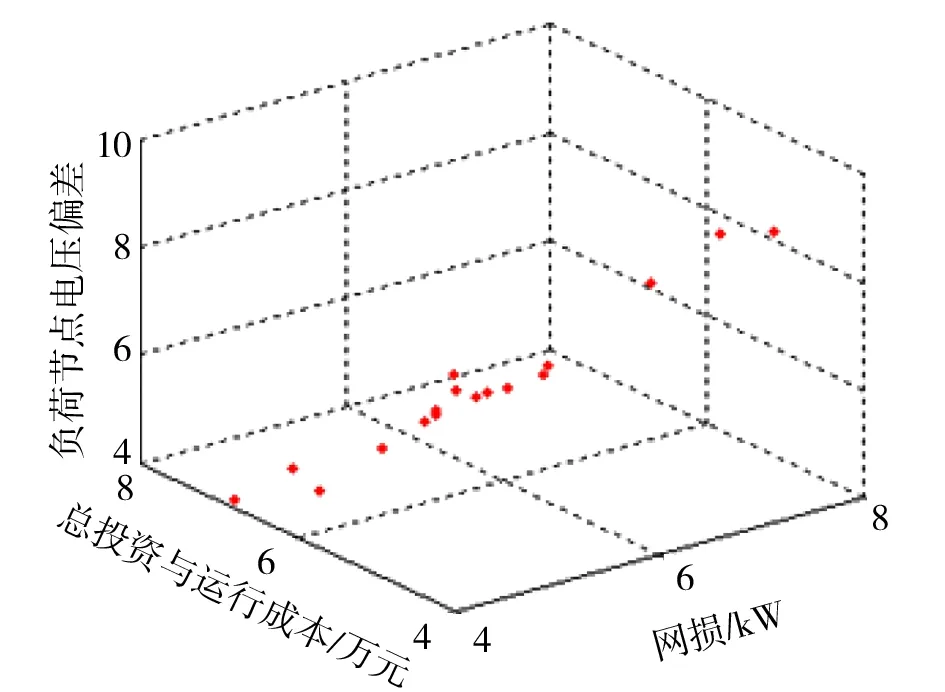
图3 Pareto解集前沿面

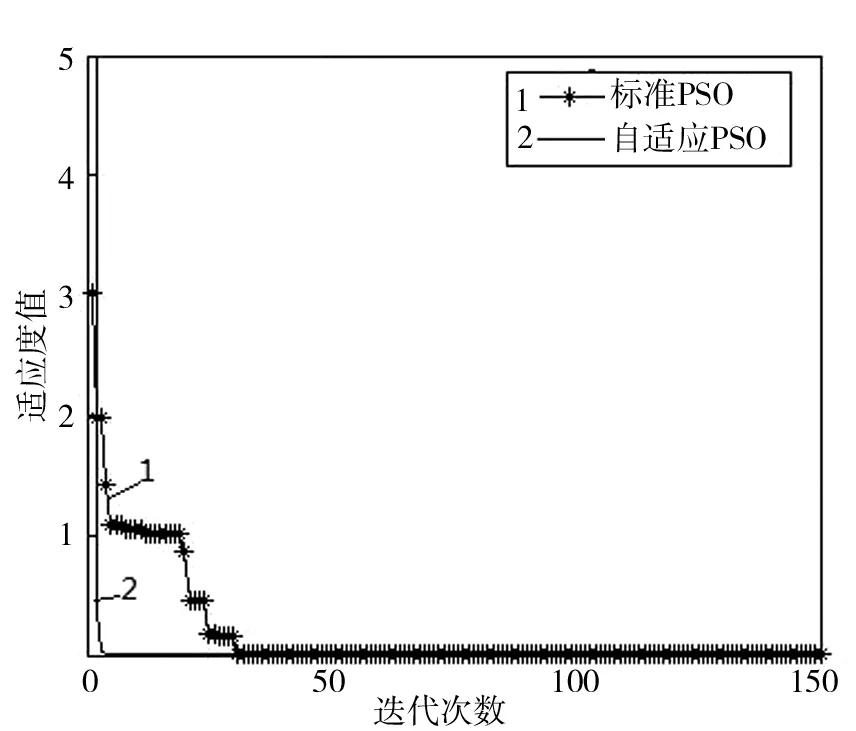
图4 迭代次数与适应度关系图

假设IEEE33节点中可以安装DG的节点为3，5，13和17，每一台分布式电源能安装的容量为50 kW，优化配置结果见表2。

表2 优化配置结果

表2中规划方案1为考虑了分布式电源的规划方案，规划方案2为忽略了分布式电源和负荷的不确定性的规划方案。规划方案1中，前一个数字表示安装的位置，括号里的数字表示安装台数和安装容量。从规划方案1可知，分布式电源安装容量都较合理，投资运行总费用、网络损耗和节点电压偏差明显降低，配电网运行得到优化。仿真结果表明，文中建立的模型能够有效地减少分布式电源的投资运行成本，降低系统有功网络损耗和减少电压偏差，这与实际情况相符。

4 结语

本文以分布式电源投资运行总成本、配电网网络损耗和节点电压偏差为目标函数，建立了分布式电源优化配置模型，将自适应权重的粒子群算法对IEEE33节点算例进行仿真求解，得出以下结论：

1)自适应更新权重能够有效地解决分布式电源多目标优化配置问题，且收敛速度快，适应度高，采用的算法具有一定的优越性。

2)本文所建立的数学模型和算法能够为含分布式电源的配电网规划提供借鉴，可以减小分布式电源的建设成本及网络损耗，对含分布式电源的经济、可靠及安全运行具有重要意义。