基于指数分布混合治愈模型的客观贝叶斯分析
肖 翔,吴懿祺,古 晞
(1.上海工程技术大学 数理与统计学院,上海 201620;2.上海对外经贸大学 统计与信息学院,上海 201620;3.同济大学 数学科学学院,上海 200092)
混合分布模型常用于对混合计数数据的研究[1−4].其中混合治愈模型在医学上有着广泛的应用,它最早是在癌症临床研究中提出的,用于解决治愈率估计问题.目前,国内外学者在对混合治愈模型的研究中取得丰富的成果.Boag[5]基于对数正态分布构建易感群体的生存函数和混合治愈模型,对癌症复发的可能性进行预测.Farewell[6]利用威布尔分布建立关于治愈率的Logistic 回归模型,用极大似然法估计参数.Ghitany 等[7]引入协变量建立基于指数分布混合治愈模型,采用极大似然法估计参数的相合性和渐进正态性.Taylor[8]使用Kaplan-Meier 估计量对易感群体的失效时间建模,引入协变量对治愈率建立回归模型,并利用EM 算法得到参数的估计值.Peng 等[9]采用非参数估计方法建立基于比例风险的混合治愈模型,并对乳腺癌数据进行实证分析.Zhou 等[10]使用多重插值补获得治愈概率和未治愈的患者生存函数的参数和方差估计.Diao 等[11]针对具有存活率的当前状态数据,提出一类半参数变化治愈模型,并证明模型回归系数的极大似然估计具有一致性、渐进正态性和渐进有效性.Lam 等[12]提出聚类加权广义估计方程方法,使用基于Bernstein 多项式的伪似然法估计模型的参数和非参数分量.
上述文献一般采用传统的或者基于EM 算法的极大似然估计法、多重插值补和伪似然法对治愈模型或者混合治愈模型中的参数进行估计,很少采用Jeffreys 先验和reference 先验等客观先验,这一领域研究几乎空白.因此,本研究使用客观先验对基于指数分布且含有删失数据的混合治愈模型进行客观贝叶斯分析.
1 基于指数分布的混合治愈模型
假设被研究总体分成两个群体:一类是治愈人群,其治愈率为p(0

假设易感人群的生存时间服从指数分布,其概率密度为
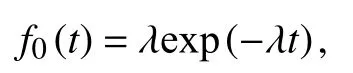
式中:λ>0.对应易感人群的生存函数为S0(t)=exp(−λt),代入式(1)得到基于指数分布混合治愈模型为
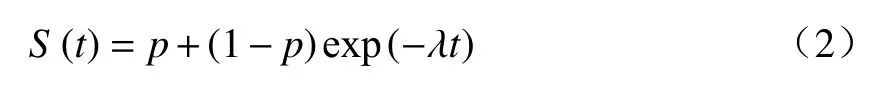
假设{(ti,di)}(i=1,2,···,n)是样本容量为n的观测值,参数(p,λ)的似然函数为
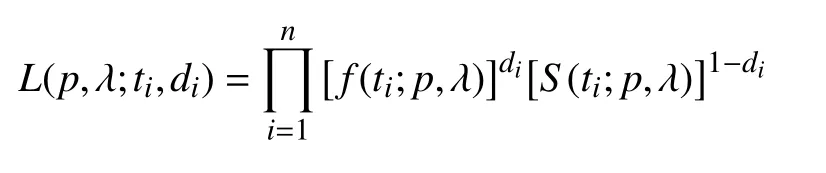
式中:f(ti;p,λ)为生存时间的概率密度函数;S(ti;p,λ)为生存函数.
若生存时间为服从指数分布的混合治愈模型式(2),则 (p,λ)的似然函数可以进一步写成
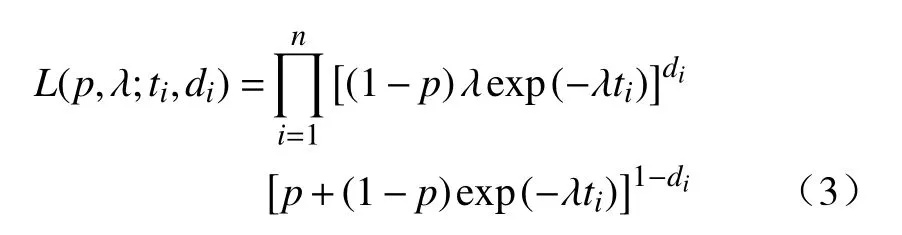
其对数似然函数为
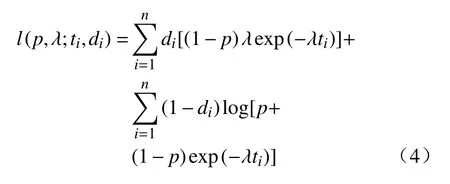
由于式(3)、式(4)比较复杂,不利于客观先验的计算,因此引入隐变量Z=(z1,z2,···,zn). 当zi=0时,个体i来源于易感群体;当zi=1时,个体i来源于治愈群体,该群体占总体的比例为p.zi是服从治愈率为p的伯努利分布,即zi~Bernoulli(p),且E(zi)=p,i=1,2,···,n.因此,基于扩充数据{(ti,di,zi)}得到参数(p,λ)的完全似然函数为
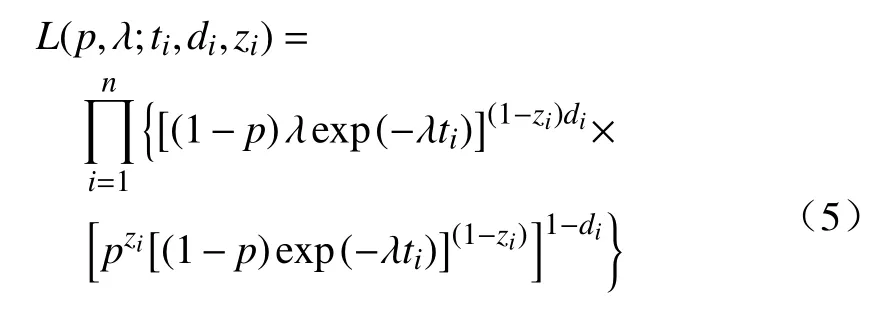
其对数完全似然函数为
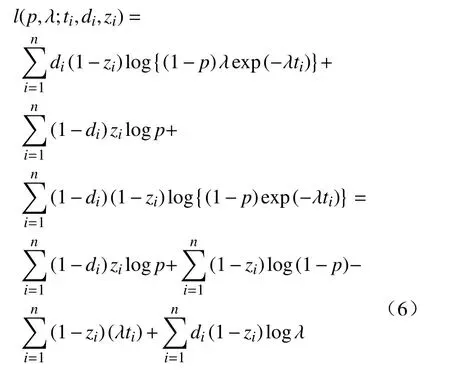
2 客观贝叶斯分析
2.1 Fisher 信息矩阵
由于原始的对数似然函数式(4)非常复杂,本节采用对数完全似然函数式(6)进行推导,得到Fisher 信息矩阵是对角矩阵,极大地简化了客观先验的计算.
定理1假设对研究对象的观测时间足够长,则基于指数分布混合治愈模型式(2),参数 (p,λ)的Fisher 信息矩阵为
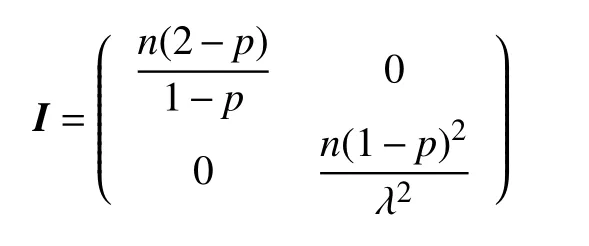
证明:对数完全似然函数式(6)的一阶和二阶偏导数为
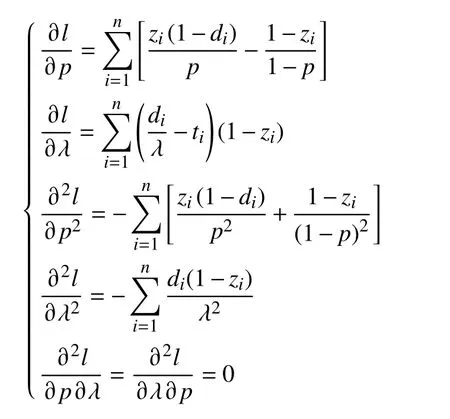
记 为失效人数,假设对研究对象的观测时间足够长,这样就可以识别出治愈者,通过样本数据观测到的未治愈率无限趋向于总体未治愈率 1−p,为后续计算方便,本研究取r≈n(1−p),得到Fisher 信息阵的组成元素为
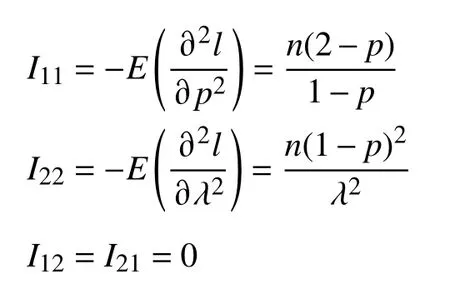
则在数据扩充策略下,参数 (p,λ)的Fisher 信息矩阵为
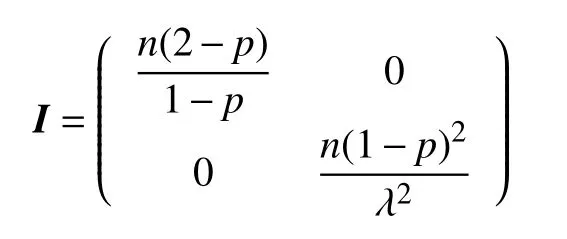
2.2 客观先验
相比于Laplace 先验,Jeffreys 先验能够在参数变换下保持不变性,比Laplace 先验具有更广泛的应用场合[13].
定理2参数 (p,λ)的Jeffreys 先验为
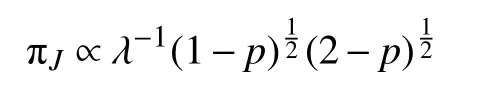
证明:参数(p,λ)的Jeffreys先验与Fisher信息矩阵行列式的平方根成正比,且有
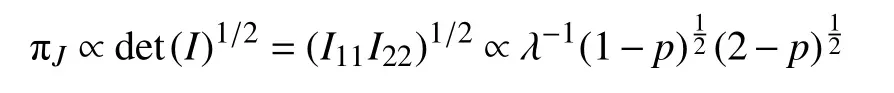
reference 先验是基于信息量准则推导出的先验分布,能够使参数的先验分布和后验分布之间的Kullback-Liebler 距离最大.reference 先验是Jeffreys 先验的推广,当参数是一维时,reference先验就变成了Jeffreys 先验.
reference 先验根据参数的重要性,可得到不同重要次序下的参数组合.例如,记号{p,λ}表示p为感兴趣参数,λ为讨厌参数,p比λ更重要.反之,记号{λ,p}表示λ为感兴趣参数,p为讨厌参数,λ比p更重要.
定理3对于参数组合{p,λ},(p,λ) reference 先验为
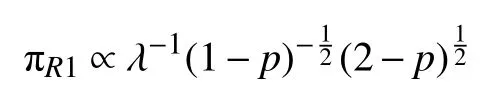
证 明:对于参数组合 {p,λ},p为感兴趣参数,Fisher 信息矩阵I可写为

式中:p∗和 λ∗为参数空间中事先给定的值.
定理4对于参数组合{λ,p},(p,λ)的reference先验为

式中:p∗和 λ∗为参数空间中事先给定的值.
从定理3 和4 的结论可以看出,无论p为感兴趣参数,还是 λ为感兴趣参数,它们的reference 先验相同,为后续讨论方便,记 πR=πR1= πR2.
2.3 后验分析
定理5基于先验分布 πJ和 πR,数据扩充策略下(p,λ)的后验分布都是恰当的.

结合式(8)和(9),可得
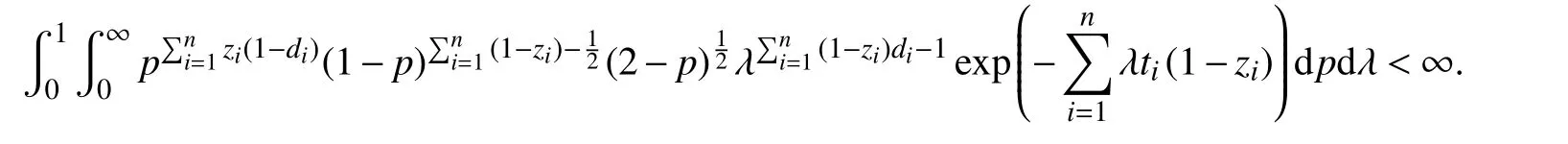
因此,基于先验分布πR,(p,λ)的后验分布πR(p,λ|ti,di,zi)是恰当的,同理,基于先验分布πJ,(p,λ)的后验分布πJ(p,λ|ti,di,zi)也是恰当的.从而,保证了后验样本抽样的可行性,如果后验分布不是恰当的,则无法抽样得到后验样本.
2.4 抽样算法设计
基于完全似然函数式(5),本节设计后验样本的Gibbs 抽样机制.
首先,设计条件分布,对隐变量Z=(z1,z2,···,zn)进行抽样,公式为
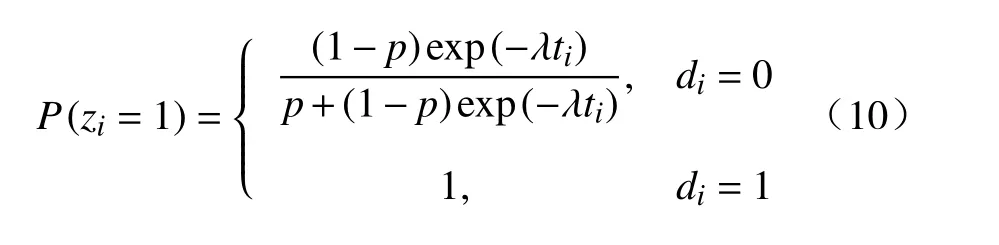
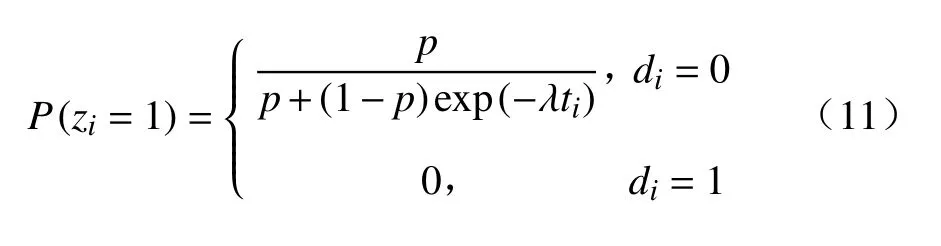
在给定Z=(z1,z2,···,zn)的条件下,从后验分布πR(p,λ|ti,di,zi)中分别抽取参数p和λ的后验样本.从式(7)可以得到p的满条件后验分布为
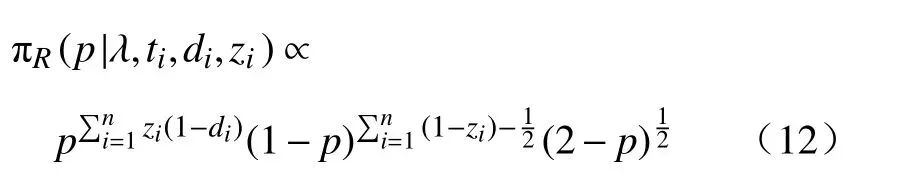
对logπR(p|λ,ti,di,zi)求关于p的二阶导数

式(13)说明p的满条件后验分布式(12)是对数上凸的,满足自适应拒绝抽样法(ARS)的使用条件.
另外,从式(7)可以得到 λ的满条件后验分布为
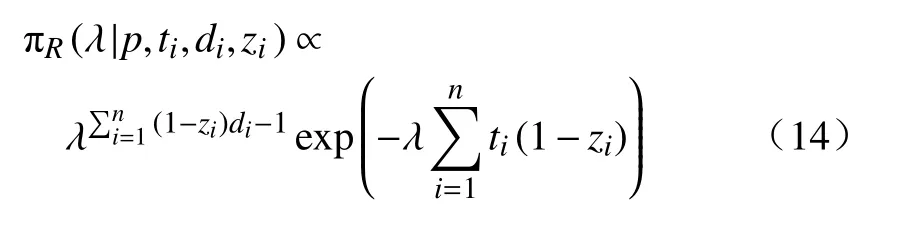
可见,λ的满条件后验分布(14)服从形状参数

最后,实施Gibbs 抽样,具体步骤如下.
1) 设定参数初始值p(0),λ(0).
2) 对t=1,2,···,实施迭代更新:
(i)利用上一步的参数估计p(t−1),λ(t−1)及式(10)和式(11),得到隐变量Z=(z1,z2,···,zn)的 样本,i=1,2,···,n;
(ii) 对式(12)采用自适应拒绝抽样法(ARS),抽样得到样本p(t);
3 数值模拟
本节分别基于先验分布πJ和πR,对p和λ进行贝叶斯估计.设置3组不同的参数真值:1)p=0.3,λ=3;2)p=0.3,λ=4;3)p=0.4,λ=4,样本容量分别设置为n=20和n=50.每次模拟均重复1000次,并从估计偏差(Bias)、均方误差(RMSE)和95%覆盖率(CP)3 个方面对估计效果进行评价,见表1 至表3.

表1 客观贝叶斯估计下的估计偏差Table 1 Bias under objective Bayesian estimation

表2 客观贝叶斯估计下均方误差Table 2 RMSE under objective Bayesian estimation

表3 客观贝叶斯估计的95%覆盖率Table 3 95% coverage probabilities under objective Bayesian estimation
从表中可以看出,随着样本容量的增加,客观贝叶斯估计下的估计偏差与均方误差都在降低,说明参数的点估计效果在逐步提高.同时,随着样本容量的增加,估计效果的差异在降低,说明客观先验在样本量小时优势比较明显.从参数估计95%覆盖率来看,两种客观贝叶斯先验下的估计结果都相对比较稳定,基于reference 先验的估计效果比基于Jeffreys 先验的效果更稳定,这是因为reference 先验比Jeffreys 先验更擅长处理多维参数的估计.
4 结语
本研究讨论了基于指数分布的混合治愈模型及其客观贝叶斯分析方法,基于完全似然函数,写出了参数的Fisher 信息矩阵,较为简洁地计算出参数Jeffreys 先验和reference 先验,并验证了后验分布的恰当性,这种方法可以推广到更复杂的混合治愈模型.今后将引入协变量信息,建立关于治愈率的回归模型,制定个性化诊疗策略.

