引信非线性宇称时间对称无线装定系统信息双向传输方法

李长生， 董文杰， 曹娟， 朱传俊， 张合

(1.南京理工大学 智能弹药技术国防重点学科实验室， 江苏 南京 210094；2.南京工业职业技术大学 机械工程学院， 江苏 南京 210023)

0 引言

非线性宇称时间对称无线电能传输技术首次报道出现在2017年《Nature》期刊上[1]，具有电路拓扑简单、鲁棒性强的突出优势。该技术应用于引信无线装定领域，可以克服目前普遍使用的电磁感应和传统磁共振方式传输距离近、鲁棒性差的缺陷，提高无线装定系统灵活性和适用范围[2-4]。文献[2]论证了该装定方案的可行性，并研究了收发端变间隙下系统功率和效率的传输特性。但是，除实现对引信装定接收电路无线供能外，还必须解决装定器与引信间的信息双向传输问题。

电磁感应和传统磁共振无线电能传输原理提出较早，信息正向加载及反向传输方法研究较为深入，已在引信装定、工业生产、消费类电子、医疗诊察等领域得到应用，彰显出旺盛的生命力。分离的收发端间信息双向传输最简单的解决方案是借用成熟无线通信方式，如蓝牙、射频通信等，也可额外增加一对线圈专门用于信息传输[5]，但这样显然增加了系统复杂度和体积。通过适当调制手段将信息加载到能量载波中，可实现单一通道下的能量与信息同步传输。众多学者探讨了传统调制方法在无线电能传输系统中的应用，包括幅度移位键控[6]、频率移位键控[7]、相位移位键控[8]。其中归零调制法是目前最常用和方便的调制方式，通过控制发送线圈上能量载波的有无来区分0或1，实质上是幅度移位键控中的一种通断键控(OOK)调制法[9-10]，但传输信息0时无法同时发送能量，降低了能量传输效率，且线圈端电压存在反复起振和停振过程，限制了信息传输速率的进一步提高。除上述传统调制方法外，学者们为提高数据传输速率或降低信息加载对能量传输的影响，探讨了其他信息加载方法。其中，高频载波信息加载法[11-12]首先将需要传输的数据调制到高频载波，然后叠加到低频能量信号，接收端利用滤波器可将信息从能量信号中提取出来，该方法中低频能量信号对高频信息载波的干扰，是需要考虑和解决的问题。文献[13]提出了谐波通信法，波形的基波分量用于传输能量，而高次谐波用于传递信息，具有可同时传递信息和能量的优点，但同时面临开关频率变化、谐波成分丰富的挑战。能量/信息频分复用法通过对传输过程电路拓扑的调整改变，使系统具有2个不同的谐振频率点，能量和信息传输分别工作在不同的谐振频率处[14-15]，该方法也可实现信息的反向传输，但存在拓扑结构复杂、不同频率载波串扰的问题。从接收端至发送端的信息反向传输方法比较单一，主要采用负载调制法，即通过对接收端用电负载并联阻抗或短路来改变系统等效负载，从而引起发送线圈端电压或电流幅值变化，发送端通过检测该电压或电流幅值的变化识别出反馈信息[10，16-17]。但是，采用负载调制法进行信息反馈时，用电负载被并联支路或短路，降低了负载电能接收总量。以上各种方法都是针对电磁感应和传统磁共振原理提出的。

因非线性宇称时间对称无线电能传输技术近年才出现，相关研究主要集中在理论建模、能量传输特性分析、传输效率优化提高等方面。文献[1，18]基于耦合模理论建立传输系统模型，得到传输效率的解析表达式。RADI等[19]和Liu等[20]利用金属板电场耦合代替文献[1]中的线圈磁场耦合，拓宽了非线性宇称时间对称无线电能传输的实现方式。Assawaworrarit等[21]和Zhou等[18]各自对电路拓扑进行了优化改进，采用半桥逆变器代替运放作为能量发送端驱动器，并通过提取回路电流信号作为逆变器开关控制信号，构成非线性宇称时间对称电路拓扑，提高了能量传输总体效率。董文杰等[2]和Li等[22]基于互感耦合理论建立了收发端参数对称及非对称条件下的传输系统电路模型，分析了参数对能量传输特性影响规律，Dong等[23]提出了一种新型的电流型非线性宇称时间对称电路拓扑。目前，尚未见能量传输通道中信息双向传输方法的文献报道。

非线性宇称时间对称无线电能传输原理具有强鲁棒性的特点，工作频率可根据参数变动自适应跟踪调整，因此信息的加载和反向传输较电磁感应和传统磁共振具有自身特殊性。信息正向传输虽然采用现有OOK调制技术也可实现，但如前所述，该调制方式会对能量传输产生负面影响。另外，信息反向传输不适用负载调制方法，特别在强耦合区，因系统的工作频率可自适应跟踪调整，负载调制技术不能引起发送端电压或电流的变化。

本文首先建立传输系统微分方程，推导收发端回路中电压和电流的瞬态响应表达式。研究单一通道下兼顾能量高效传输和信息快速可靠传输的信息同步加载方法，减小信息加载对能量传输产生的负面影响。然后探讨工作频率自适应跟踪下的信息反向传输方法。最后通过实验验证本文信息双向传输方案的可行性。

1 装定系统瞬态响应模型

1.1 理论建模

基于非线性宇称时间对称无线电能传输原理的引信无线装定系统如图1所示[2]。图1中：R1与运算放大器A构成负电阻，用于将装定器电源提供的直流电转化为交流电，为耦合系统供电；L1、L2分别为发送线圈和接收线圈的自感；M为两线圈间互感；C1和C2分别为发送端与接收端的匹配电容，用来设定发送与接收回路的固有谐振频率；RF为运算放大器的反馈电阻，RG为运算放大器的增益电阻，通过调整RF与RG的值可以设置运算放大器线性区的电压放大倍数；R2为接收端的负载等效电阻；V1和V2分别为发送端与接收端的线圈两端电压；I1和I2分别为发送端与接收端线圈中流过的电流；Vo为运算放大器的输出电压。

图1 引信无线装定系统原理图Fig.1 Schematic diagram of fuze wireless setting system

基于互感耦合理论[2-3]，由基尔霍夫电压及电流定律可得

(1)

记V1=x1，V2=x2，I1=x3，I2=x4，则由(1)式可得

(2)

式中：ρ1=1/C1；ρ2=1/C2；ξ1=1/R1；ξ2=1/R2；σ1=1/(L1(1-κ2))，κ为发送和接收线圈之间的耦合系数；

(3)

运算放大器的理想饱和非线性如图2(a)所示[24]。图2(a)中，kop为运算放大器在线性区的电压放大倍数，kop=(RG+RF)/RG；[-a，a]为运算放大器的线性区域，a为饱和度；Vi为运算放大器的输入电压。由图2(a)可知，线性区和饱和区存在非线性过渡，这对系统时域响应分析十分不利，会大大增加数值计算耗时。因此，为提高数值计算精度、降低计算难度，需要采用更加平滑的饱和非线性来对运算放大器的饱和特性曲线进行建模，如图2(b)所示。

图2 运算放大器的饱和非线性示意图Fig.2 Saturation nonlinear diagram of operational amplifier

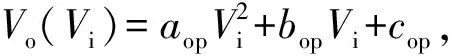
(4)

进一步可得

(5)

Vi=bb代入二次函数中，可得到完全饱和区域的输出值dop，

(6)

(7)

结合(2)式和(7)式，采用龙格- 库塔法对V1、V2、I1、I2进行数值求解，便可获得收发端回路中电流和电压波形的时域数值解。

1.2 仿真验证

本文如无特殊说明，所有仿真计算和实验测试均基于表1参数进行。其中：收发端线圈均采用直径1 mm的铜漆包线各匝并排密绕而成，匝数为7匝，线圈直径90 mm；该传输参数下，临界耦合系数κc=0.019，对应收发端距离约107 mm.当κ>κc时，为强耦合区，系统存在2个谐振频率；当κ≤κc时，系统仅存在1个谐振频率[2]。表1参数代入(7)式，求解出V1和V2的波形如图3所示。从图3中可以看出，系统上电后发送端快速起振，待系统稳定后V1和V2的幅值基本相同，与文献[1]所描述的一致。接收端起振至稳定运行需经历一定时间的振荡调整，主要因为接收端是从发送端电磁耦合拾取的电能，为受迫振荡。稳定运行后，收发端电压幅值均不再发生变化。理论计算值与PSpice软件仿真值十分吻合，证明了理论模型的正确性。

表1 传输系统参数Tab.1 Transmission system parameters

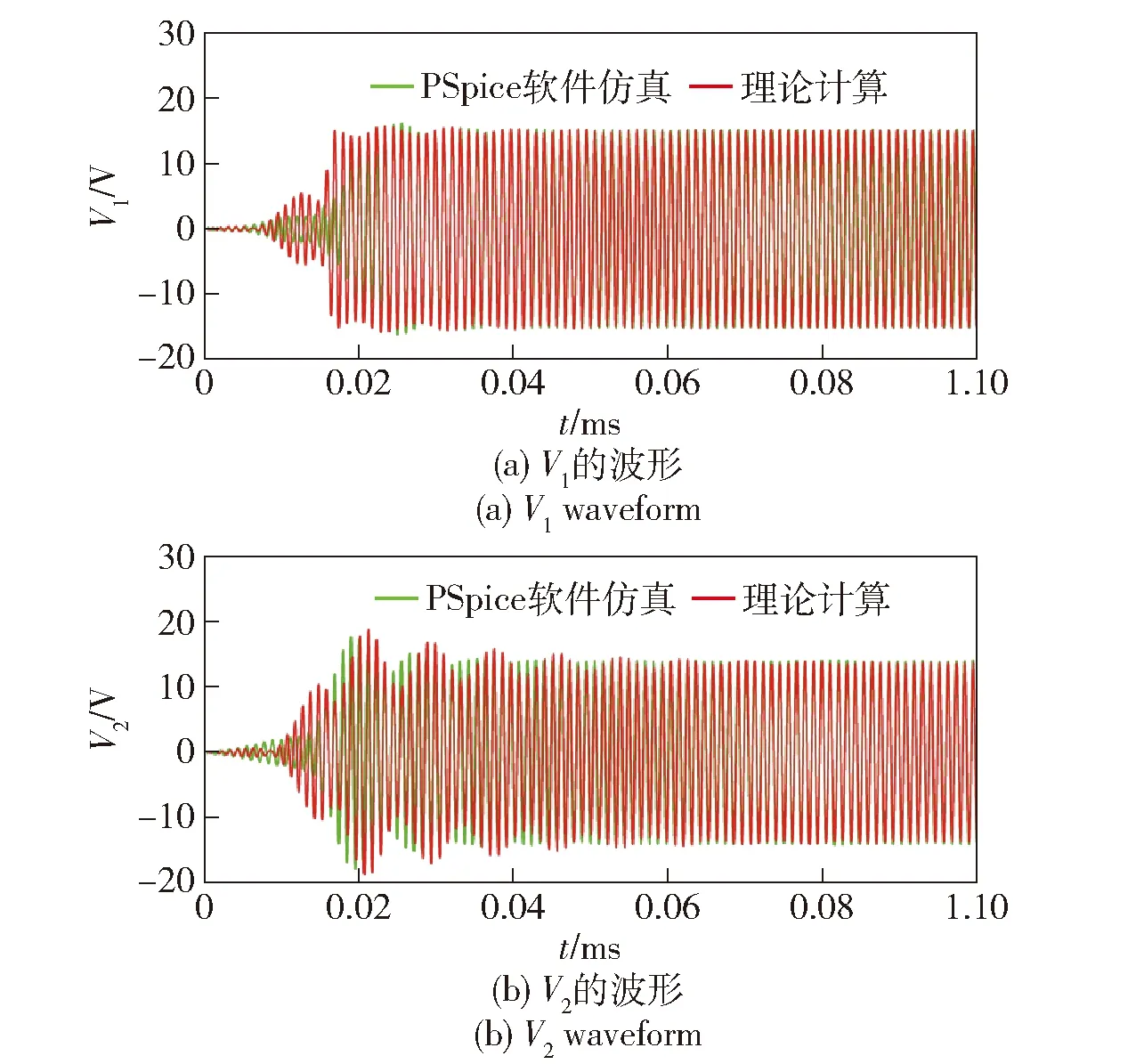
图3 收发端回路电压波形时域仿真对比Fig.3 Simulation comparison of voltage waveforms of transceiver circuit in time domain

2 信息正向传输

2.1 基于非归零调幅的信息正向传输加载方法

信息正向传输阶段(装定器至引信装定接收电路)，通过改变发送线圈端电压幅值，从而影响接收线圈端电压幅值的变化，以实现能量波形中的信息加载，是可行方案。传统OOK调制方法属于一种归零调制法，即发送信息“0”时，线圈端电压为0 V，无法传递能量，且信息“0”与“1”间变换时回路存在起振和停振过程，限制了信息传输速率的提高，如图4(a)所示。采用非归零调幅信息加载方法，如图4(b)所示，发送信息“0”时，不再要求线圈端电压降至0 V，而是低于信息“1”一定幅值即可。该方式与传统OOK调制方法相比，能量传输是连续的，单位时间内可以传输更多电能，平均传输功率得以提高。另一方面，非归零调幅加载方法由于收发端一直处于谐振状态，信息加载只是线圈端电压幅值的改变，回路不需要反复起振、停振，传输速率得以提高。工程应用中，可以通过改变运放供电电压的方式方便实现非归零调幅信息加载。例如，传输信息“1”时采用V1i电源供电，传输信息“0”时采用V2i电源供电，二者切换采用电子开关快速完成。图4中，Vm、Im分别为线圈端电压、电流幅值，V0m、V1m分别为传输信息“0”、“1”时线圈端电压幅值。

图4 信息正向加载示意图Fig.4 Schematic diagram of information forward loading

信息正向传输时，数据“1”和“0”的发送概率均为50%. OOK调制方式，在不考虑回路起振和停振情况下，信息传输段相对纯电能传输时平均传输功率下降50%. 本文提出的非归零调幅加载方式，假设发送信息“0”时幅值为“1”时的a% (V0m/V1m=a%)，则信息传输段相对纯电能传输时，平均功率下降(50-0.5a)%. 通过提高数据“0”时电平幅值，可进一步降低信息加载对能量传输的负面影响。文献[2，22-23]已对系统传输功率、效率、参数变动影响规律进行了详细讨论，本文只讨论信息加载过程对能量传输的相对影响，不再探讨不同传输阶段或传输条件下的具体功率和效率数值。

2.2 数值仿真分析

定义非归零调幅的两种状态：传递“1”时，电源供电电压V1i=±15 V；传递“0”时，电源供电电压V2i=±5 V，两电源切换频率20 kHz. 根据本文理论模型，数值求解后的V1和V2波形如图5所示。从图5中可以看出：发送线圈两端电压V1的幅值随着供电电源电压的变化而变化，而且切换过程几乎不影响系统的谐振；接收线圈两端电压V2幅值随着V1幅值的变化同步改变，但是由于V2是由V1感应而来的，幅值切换瞬间存在短暂振荡调整过程，特别是系统上电的初始启动段，起振调整明显，后续状态基本保持稳定；V2的波形变化明显，能够区分出“1”和“0”两种状态，通过包络检波电路可以实现正向信息传输的解调。

图5 信息正向传输数值仿真波形Fig.5 Numerically simulated waveform of forward information transmission

3 信息反向传输方法

3.1 基于失谐调频的信息反向传输方法

如引言部分所述，因非线性宇称时间对称系统的频率自适应跟踪调整特性，不适合采用电磁感应和传统磁共振方式中的负载调制实现信息反馈。针对该原理传输系统，文献[24]提出一种通过调整接收端谐振电容值，造成接收端失谐，从而实现系统谐振频率选择和控制的方法。但是该方法在工程实现时，调整电路必然存在一个常闭开关，增加了接收端电能消耗。针对以上问题，本文提出图6所示的调控方式。图6中，L2和C2使得接收回路固有谐振频率与发送端一致，正常工作状态下开关S1和S2均处于常开状态，只在需要信息反馈时才短暂闭合，f10和f20分别为强耦合区的高频、低频谐振频率分支点，f3为低频失谐点，f4为高频失谐点。

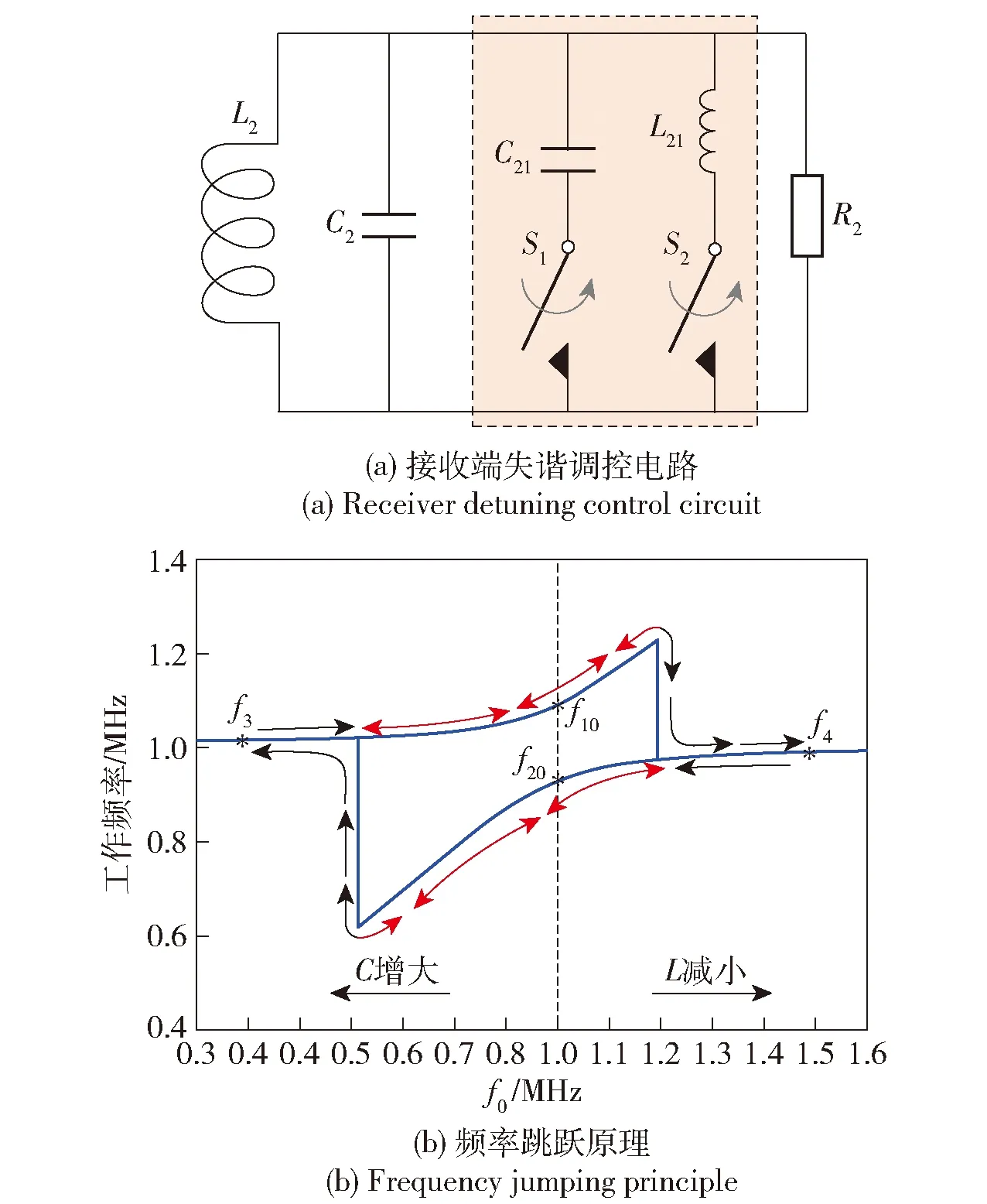
图6 基于接收端失谐的谐振频率调控方法Fig.6 Resonant frequency control method based on the receiver detuning

以κ=0.163时的频率调控为例，失谐调频原理如图6(b)所示，失谐方法可通过增大C或减小L的等效值实现。收发端匹配的传输系统启动时，会运行在f10或f20中的一个谐振频率点处，并具有一定随机性，不可控。假设系统启动时运行在f20处，频率跳跃遵循最短路径原则[24]。某时刻，将开关S1闭合、S2断开，C21接入回路，系统失谐运行于f3处。然后断开S1，因频率选择具有惰性，遵循最短路径原则，系统不会回到原f20处，而会就近选择运行于f10处，从而实现了从谐振频率f20至f10的跳跃。若初始状态系统运行在f10处，则某时刻，开关S1闭合，系统同样失谐运行于f3处。断开S1后，就近沿高频谐振分支回复到f10处运行，而不会跳跃到较远距离处的f20处。

接下来分析开关S2的作用。同样，首先假设系统启动时运行在f20处。某时刻，将开关S1断开、S2闭合，L21接入回路，系统将失谐运行于f4处，然后断开S2，因频率选择具有惰性，遵循最短路径原则，谐振频率沿原路径回复到f20处。若初始状态系统运行在f10处，则开关S2闭合，系统失谐运行于f4处，断开S2后，选择最近的谐振频率f20处运行，而不会回复到远距离的f10处，从而实现了从谐振频率f10至f20的跳跃。通过以上分析发现：开关S1闭合后再断开，就能诱导系统选择高频谐振分支；开关S2闭合后再断开，就能诱导系统选择低频谐振分支。

因此，可以利用图6(a)失谐调控电路，依据图6(b)频率选择原理，通过接收端控制开关S1、S2的闭合或断开，控制系统在指定频率分支上运行。发送端通过检测发送回路频率变化，获取接收端反馈信息。理论上，谐振频率可在很短的失谐时间内完成跳跃，便于反馈信息的快速传输。接收端信息反馈过程中，除去短暂的失谐诱导过程，收发端始终处于谐振状态，有效减小了信息反馈过程对能量传输的负面影响。因这种失谐反馈方法系统工作频率需要在2个谐振频率分支上跳跃，故只适用于κ>κc的强耦合区。实际上κ<κc的松耦合区因传输效率显著下降且衰减迅速，可用范围及场合较少。

反馈信息中，数据“1”和“0”出现的概率均为50%.传统信息反馈负载调制方式，不论是对用电负载并联阻抗还是直接短路，开关闭合期间，用电负载都几乎接收不到电能；信息反馈阶段，接收端接收到的电能较纯电能传输阶段下降50%.本文提出的失谐调频信息反馈方法，假设每位数据传输时间为t1，图6(a)中开关S1或S2的闭合时间为t2，闭合时系统严重失谐，接收的能量较少，近似为0 V.因此，该调制方法信息反馈阶段，将造成系统传输功率下降(50×t2/t1)%.通过减少开关S1和S2的闭合时间t2，可降低信息反馈对能量传输的影响。

3.2 数值仿真分析

为满足3.1节频率跳跃条件，图6(a)中C21取值6.43 nF，L21取值3.04 μH，具体控制时序如图7所示。起振阶段，系统工作在哪一频率分支是未知的，某一时刻，闭合开关S1，将接收端回路电容调整为9.22 nF，3 μs后断开开关S1，谐振电容切换回2.80 nF，根据3.1节分析结论可知，系统将会选择高频分支运行。同理，将开关S2闭合，接收端线圈等效电感调整为2.28 μH，3 μs后断开开关S2，线圈电感值切换回9.07 μH，系统将会选择低频分支运行。图7(b)和图7(c)为数值仿真波形。从图7中可以看出，系统上电后选择了低频分支，这是无法控制的。按图7(a)时序对接收端等效电感和电容值进行调整后，系统分别选择了低频和高频分支，与理论分析结论一致。接收端电感和电容切换瞬间，与信息正向传输时类似，接收端感应电压幅值有明显振荡过程，主要是传输参数突变，接收端需要振荡调整后恢复稳定状态。不论系统运行于高频或低频谐振分支，稳定后的收发端波形幅值近似相同。因此，通过调整接收端回路中等效电抗值，控制系统工作频率，再通过提取发送端回路工作频率的方法，可实现信息的反向传输。

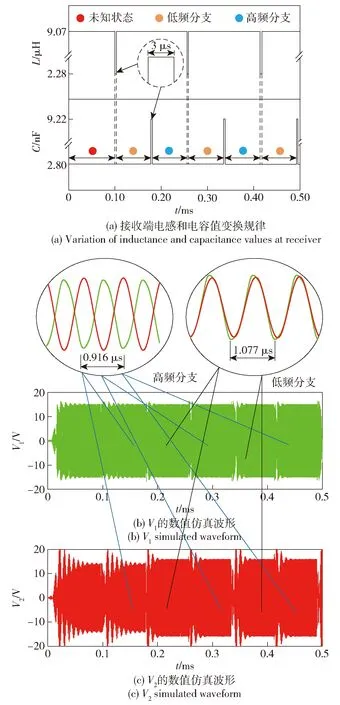
图7 基于失谐调频的信息反向传输仿真Fig.7 Simulated waveforms of information reverse transmission based on detuning frequency modulation

4 原理样机实验验证

为检验上述信息双向传输方案的可行性，设计了图8所示的原理样机验证实验。发送端运放采用±15 V和±5 V的双电源供电。信息正向传输时，由信息编码信号VS控制电子开关，完成电源电压的选择切换，该过程中接收端开关S1和S2均断开。信息反向传输时，利用反馈信息编码控制电容C21和电感L21的接入和移除，该过程中发送端采用±15 V电源电压工作。信息正向传输和反向传输分时进行，属半双工通信。实验中，收发端距离30 mm，信息正向传输时采用周期50 μs的方波控制电源电压切换；反向传输时，采用两个周期156 μs、高电平脉宽3 μs的脉冲信号VS1、VS2分别控制开关S1和S2的通断，两脉冲波的高电平上升沿时间差为75 μs.

图8 信息双向传输验证实验Fig.8 Dual-directional information transmission verification experiment

图9所示为信息双向传输测试波形。由图9(a)～图9(c)信息正向传输测试波形可以看出，收发端线圈端电压波形同步变化，发送线圈电压V1只在幅值切换处略有扰动，系统的谐振频率保持不变；接收线圈电压V2在幅值切换过程存在短暂超调和调整过渡过程。对比图9(a)～图9(c)和图5仿真波形，可以看出理论计算波形与实验测试波形十分吻合，再次证明了本文理论模型的正确性。由图9(d)～图9(g)信息反向传输测试波形可以看出，稳态运行期间，收发端幅值近似相同，除失谐调制瞬间外，高低频率分支下的幅值近似相同。发送端工作频率受接收端控制，在0.94 MHz(理论值为0.93 MHz)和1.10 MHz(理论值为1.09 MHz)二者间来回切换。频率跳跃规律与理论分析结果相同，即电容C21接入回路后再移除，系统选择高频谐振分支运行；电感L21接入回路后再移除，系统选择低频谐振分支运行。失谐电容C21和失谐电感L21接入回路3 μs后移除，即可成功诱导至相应频率分支运行，表明频率跳跃速度十分迅速，对提高信息反向传输速率十分有利。开关控制信号VS1和VS2为高电平时，接收端波形迅速失谐，低于稳态运行幅值，发送端则会有约3 μs的延时后再发生失谐和频率跳跃。这是因为与信息正向传输相比，反向传输阶段是由接收端诱导发送端产生状态变化，二者电磁耦合同样需要振荡调整时间。实验中，信息正向传输速率20 kbit/s，是文献[25]中OOK调制传输速率的2倍；反馈信息传输速率12.8 kbit/s. 因正向传输时数据“0”能量幅值降低及反向传输时的失谐调频作用，传输功率较纯电能供给阶段分别降低了33.33%和1.92%，但相对传统OOK调制和负载调制方式，分别提高了16.67%和48.08%. 信息正向和反向传输时的解调，可分别采用常规包络检波和鉴频解调法，不再赘述。

图9 实验测试结果Fig.9 Experimental test results

在完成上述信息双向传输方案验证实验后，进行装定正确率测试实验。信息正向传输测试时，利用计算机向装定器发送2字节装定信息，引信装定接收模块将接收到的信息经解调、译码后上传至计算机，通过对比发送和接收内容，判断传输结果。信息反向传输测试时，装定器向引信装定接收模块持续供能，计算机向接收模块发送2字节反馈信息，装定器解调、译码后将其发送给计算机，同样通过对比发送和接收内容判断传输正确性。测试中，统计100次传输结果，并改变收发端线圈距离，得到不同传输距离下的信息传输正确率。测试结果如表2所示。

表2 信息传输正确率测试结果

由表2实验测试结果可知：30 mm和55 mm处的强耦合区，正向和反向信息传输正确率稳定在100%；基于非归零调幅的正向信息加载方法在松耦合区仍然适用，130 mm时系统的传输正确率依然达到100%. 但随着距离的进一步增大，系统的正向传输正确率开始下降，主要因为收发端耦合系数变小，接收端感应电压幅值降低，影响信息正确识别；因系统在松耦合区高低谐振频率分支汇聚为一个频率分支，不存在谐振频率分岔现象，接收端失谐也就无法使发送端工作频率发生改变，因此不能实现信息反向传输，与理论分析结论一致。

5 结论

针对基于非线性宇称时间对称原理的引信无线装定系统信息双向传输方法开展研究，本文建立了装定系统能量传输微分方程，推导出运算放大器平滑的饱和非线性特征曲线的数学模型，求解出收发端回路电压和电流的时域瞬态响应数学表达式。根据稳态振幅特性提出一种非归零调幅的信息正向传输方法，通过调整发送端供电电压以改变耦合线圈端电压稳态振幅，而不影响系统工作频率，减小了调制过程中的起振和停振时间，从而提高信息的传输速率，同时实现信息加载过程中的能量不间断传输。根据谐振频率调控机理，提出一种失谐调频的信息反向传输方法，不论传输信号“0”还是“1”，系统都处于谐振状态，失谐只发生在两种信号切换的瞬间，失谐时间短，能量损失小，进一步保证了接收端能量的接收。基于本文理论设计的引信无线装定原理样机，信息的正向传输速率为20 kbit/s，反向传输速率12.8 kbit/s，该速率并不是传输能力的上限，还可进一步提高，且文中所提信息双向传输方法降低了能量传输通道中信息加载对能量传输性能的影响。

本文仅是对信息双向传输方法进行了原理样机验证实验，后续工程推广应用中还需解决装定系统电磁兼容性、平台适配性、装定速度等方面问题。此外，合理选择正向传输时信息调制深度，实现能量高效传输和信息可靠传输间的匹配，探寻松耦合区信息反向传输方法，也是下一步需要解决的问题。