武装直升机与空地导弹系统相容性分析
邹汝平, 陈韵, 陈士超
(中国兵器工业第203研究所, 陕西 西安 710065)
0 引言
武装直升机具有火力强、灵活机动的作战特点,有突出的超低空飞行能力,可在“一树之高”实现对威胁目标的精确打击,具有较强的战场生存能力,是陆军航空兵对地攻击、夺取超低空制空权的主要武器平台,已成为现代陆战场最主要的空中突击作战力量[1-4]。空地导弹作为武装直升机的主战武器装备,具备破甲、攻坚、侵彻、杀伤爆破等多功能毁伤效应,可对陆地、海上、超低空的多种时敏目标实施精确打击[5-9]。
然而,武装直升机作为空地导弹的挂装平台,需要充分考虑载机和导弹的相容性问题。由于直升机旋翼下洗气流的存在,在各种扰动的组合影响下,导弹的初始弹道将引起非确定性散布;直升机采用悬停、前飞、下滑等攻击方式时,不同的载机速度和姿态特性,将对空地导弹的初始发射条件和离轨飞行环境产生影响;导弹挂装在直升机短翼下方,必须针对挂架的随动范围研究导弹近机体飞行时与载机及旋翼的安全飞行包线。此外,导弹离轨发射时,需要考虑发动机尾焰对直升机机体的安全性影响。
机- 弹相容性分析涵盖空地导弹的挂飞适应性、机- 弹结构与电气分离的安全性、发射离轨动态过程以及发射后初始弹道与武装直升机的空间关系等。其中空地导弹的挂飞适应性、机- 弹分离的安全性一般通过挂飞试验、地面适配性发射测试、振动冲击条件下的结构与电气性能评估来考核验证。截止目前,国内外对于直升机载导弹机- 弹相容性的分析主要集中在旋翼下洗流对导弹的影响[10-13]。关于武装直升机不同攻击模式对导弹的影响,以及组合扰动环境下空地导弹初始弹道与载机动态影响方面的研究较少。
本文结合直升机载空地导弹挂载和发射的特点,对直升机旋翼下洗流、飞行速度、攻击方式对空地导弹初始弹道的影响,以及导弹发射离轨后与载机的相对关系、发动机喷流对载机的安全性影响等方面对武装直升机和空地导弹的机- 弹相容性进行分析研究,为直升机载空地导弹机- 弹相容性设计、攻击条件选择等提供技术支持。
1 坐标系定义
在进行多因素分析之前,首先对直升机与空地导弹相容性分析主要涉及的坐标系进行简要介绍。涉及的坐标系主要包括地面坐标系Oexeyeze、弹体坐标系Oxpypzp、弹道坐标系Oxtytzt、速度坐标系Oxvyvzv、直升机机体坐标系Obxbybzb以及相对来流坐标系Oxryrzr(弹体坐标系、弹道坐标系、速度坐标系及相对来流坐标系的原点均为导弹质心O),其中Oexeyeze、Oxpypzp、Oxtytzt以及Oxvyvzv的坐标系定义详见文献[10]。下面分别对Obxbybzb、Oxryrzr进行简要介绍。
Obxbybzb的原点Ob取在直升机的质心位置;Obxb轴与直升机的纵轴相重合,方向为指向机体头部为正;Obyb轴位于机体纵向对称平面内,与Obxb轴垂直,方向指向上为正;Obzb轴垂直于Obxbyb平面,方向按右手直角坐标系确定。Obxbybzb与Oexeyeze之间的关系由直升机的俯仰角ϑb、偏航角ψb和滚转角γb确定。
相对来流坐标系Oxryrzr的原点O取在空地导弹的质心位置;Oxr轴与导弹相对气流的速度向量vr一致,方向指向目标为正;Oyr轴位于包含导弹纵轴的纵向对称平面内,与Oxr轴垂直,方向指向上为正;Ozr轴垂直于Oxryr平面,方向按右手直角坐标系确定。Oxryrzr与弹体坐标系Oxpypzp之间的关系由相对攻角αr和相对侧滑角βr确定。Obxbybzb、Oexeyeze以及Oxpypzp的相对关系如图1所示。

图1 坐标系定义Fig.1 Definition of coordinate system
下面从多角度出发,分别对不同因素对武装直升机与空地导弹的相容性影响进行分析。
2 发射安全性建模与仿真分析
2.1 发射安全性建模
武装直升机典型的攻击方式包括悬停、平飞和下滑3种。直升机载导弹发射架与直升机有一定的相对角度关系,侧向距离机体近,且发射后弹道爬升,导弹离轨后受到下洗气流及发射扰动等的影响,需要分析发射过程中弹道与直升机相对位置关系,确保对直升机的机体(侧向)及旋翼(纵向)没有干涉影响。
要综合分析导弹发射的安全性,首先要确定挂载状态下直升机与导弹的位置结构相对关系,具体参数如表1所示,表1中各参量表征的几何结构关系如图2、图3所示。图2和图3中,Δxb、Δyb、Δzb分别表示导弹和直升机机体部位在机体坐标系Obxb轴、Obyb轴、Obzb轴中的相对位置。

表1 直升机与导弹相对关系参数Tab.1 Relative parameters of helicopter and missile

图2 表1中各参量表征的几何关系侧视图Fig.2 Lateral view of the geometrical relationship represented by the parameters in Tab.1

图3 表1中各参量表征的几何关系俯视图Fig.3 Vertical view of the geometrical relationship represented by the parameters in Tab.1
基于导弹的运动学动力学模型、直升机运动学模型及各种边界、扰动模型等,建立机- 弹相对运动仿真模型,如图4所示。图4中,xpe、ype、zpe为导弹在地面坐标系的位置坐标,ϑ、ψ、γ分别为导弹的俯仰角、偏航角、滚转角,xbe、ybe、zbe为直升机在地面坐标系的位置坐标,vb表示直升机的飞行速度。
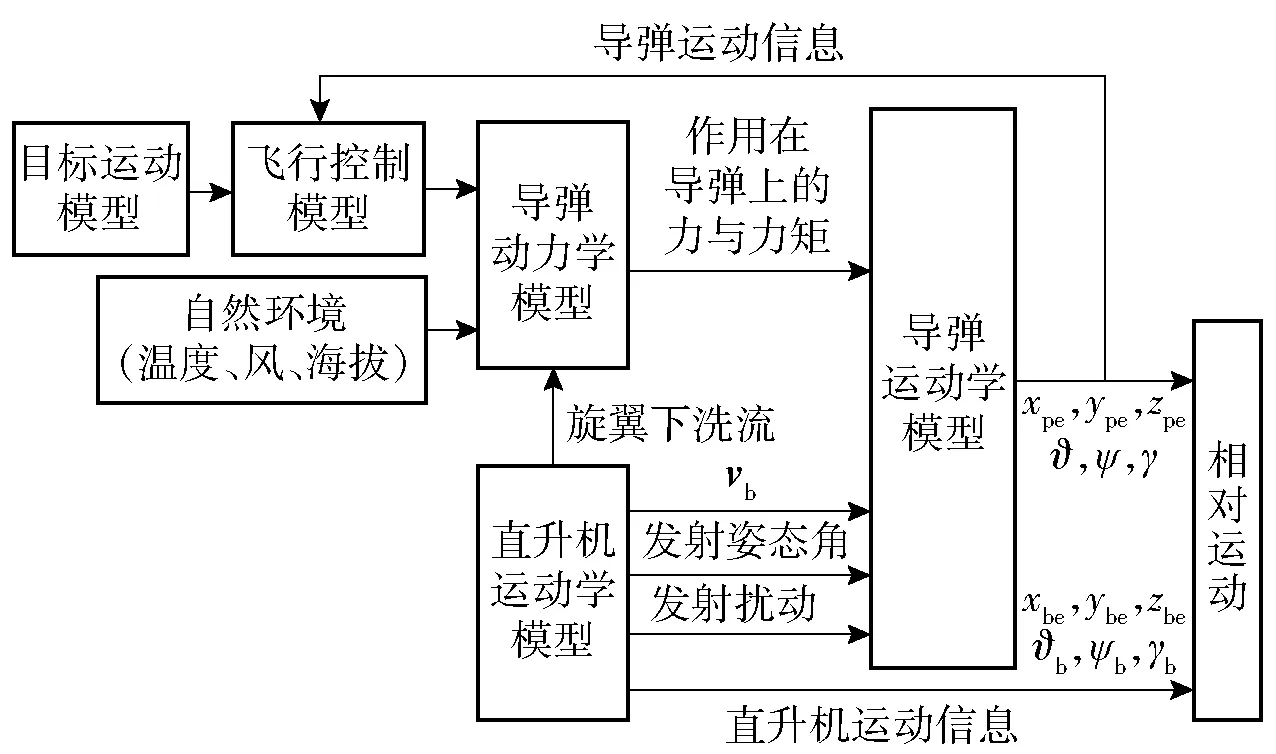
图4 机- 弹相对运动仿真模型Fig.4 Simulation model of relative motion of helicopter and missile
2.2 不同攻击模式下发射安全性仿真分析
分别对直升机悬停、平飞及下滑3种不同攻击模式进行弹道仿真,典型仿真参数如表2所示。

表2 不同攻击模式下弹道仿真参数Tab.2 Simulation parameters of missile trajectory under different attacking modes
发射架相对直升机角度设置为最大调转角度值8°,在俯仰、偏航和滚转3个方向均添加较为苛刻的初始扰动。导弹飞离直升机过程中,导弹与载机相对位置空间关系的仿真实验结果如图5~图10所示,实际飞行试验结果如图11~图14所示,图中Δx、Δy、Δz分别表示导弹和直升机在地面坐标系下的相对位置。其中:图5、图6分别对应直升机悬停攻击模式时,仿真实验结果的侧视图和俯视图;图7、图8分别对应直升机平飞攻击模式时,仿真实验结果的侧视图和俯视图;图9、图10分别对应直升机下滑攻击模式时,仿真实验结果的侧视图和俯视图;图11、图12分别给出了悬停攻击模式时,导弹实际飞行与载机相对位置的空间关系;图13、图14分别给出了平飞攻击模式时,导弹实际飞行与载机相对位置的空间关系。
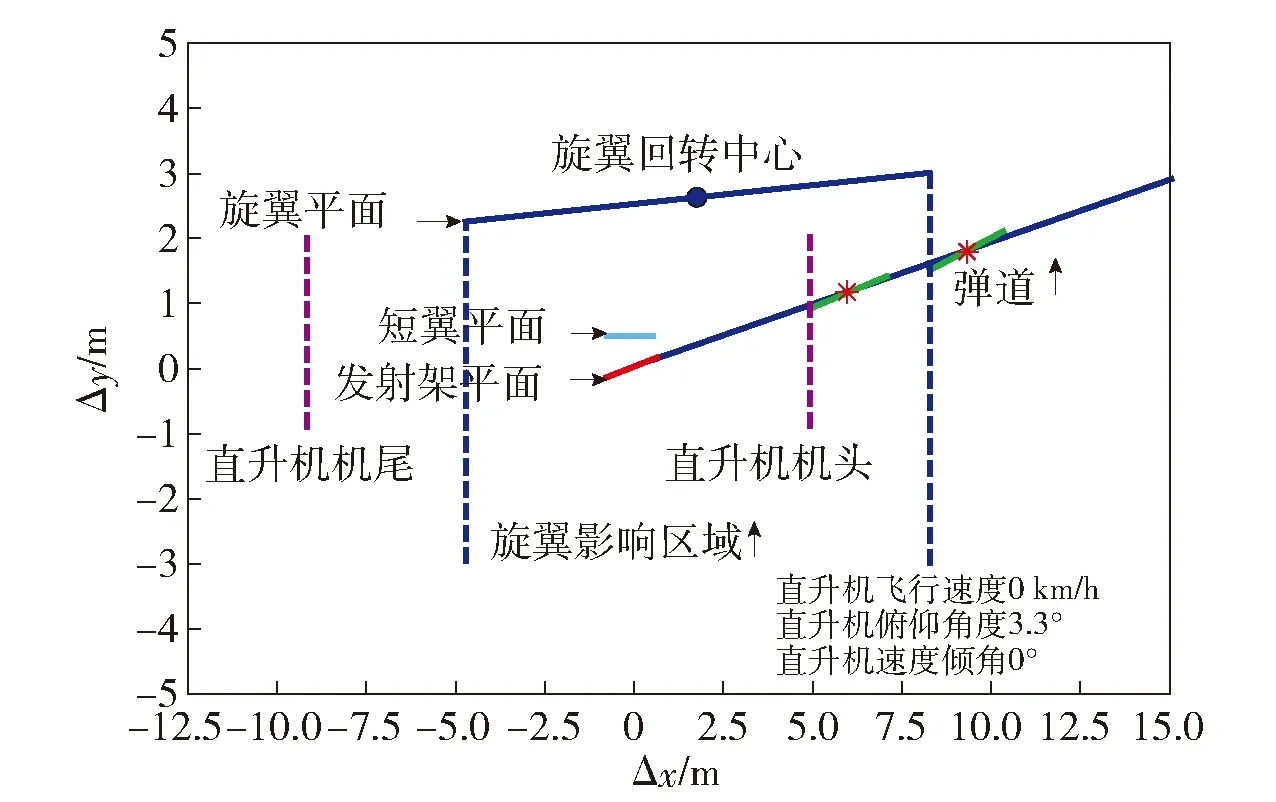
图5 直升机悬停攻击时机- 弹相对关系侧视图Fig.5 Lateral view of the relationship between the helicopter and the missile during helicopter hovering

图6 直升机悬停攻击时机- 弹相对关系俯视图Fig.6 Vertical view of the relationship between the helicopter and the missile during helicopter hovering

图7 直升机平飞攻击时机- 弹相对关系侧视图Fig.7 Lateral view of the relationship between the helicopter and the missile during helicopter level flying
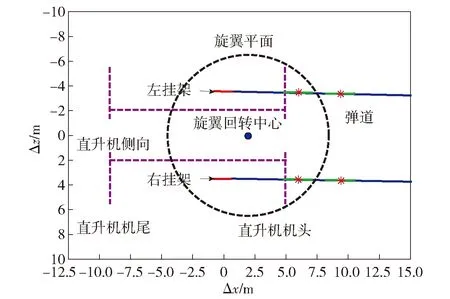
图8 直升机平飞攻击时机- 弹相对关系俯视图Fig.8 Vertical view of the relationship between the helicopter and the missile during helicopter level flying

图9 直升机下滑攻击时机- 弹相对关系侧视图Fig.9 Lateral view of the relationship between the helicopter and the missile in helicopter descent mode

图10 直升机下滑攻击时机- 弹相对关系俯视图Fig.10 Vertical view of the relationship between the helicopter and the missile in helicopter descent mode
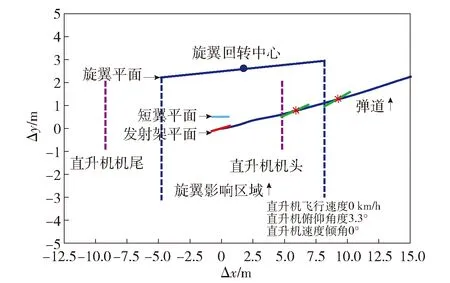
图11 直升机悬停攻击时机- 弹相对关系侧视图(飞行实验)Fig.11 Lateral view of the relationship between the helicopter and the missile during helicopter hovering (flight experiment)
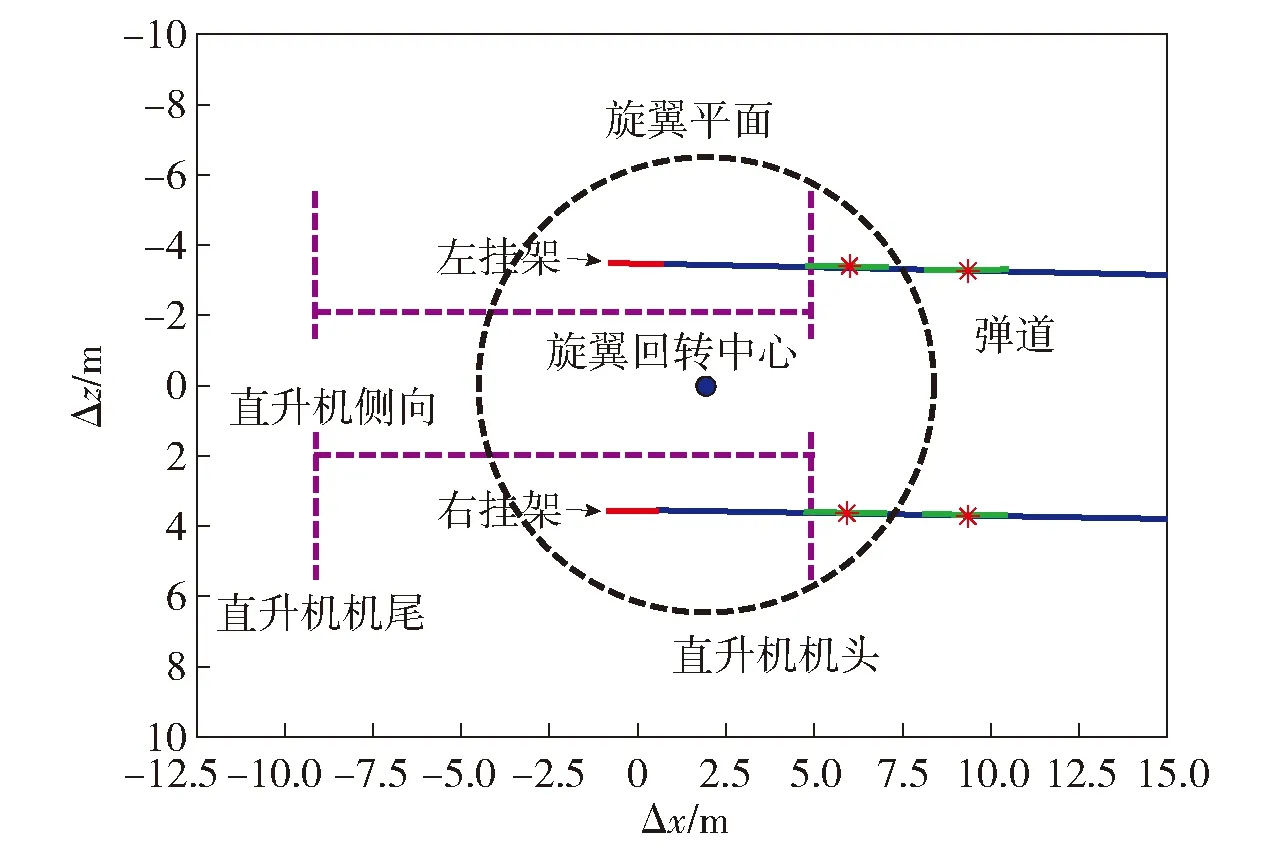
图12 直升机悬停攻击时机- 弹相对关系俯视图(飞行实验)Fig.12 Vertical view of the relationship between the helicopter and the missile during helicopter hovering (flight experiment)
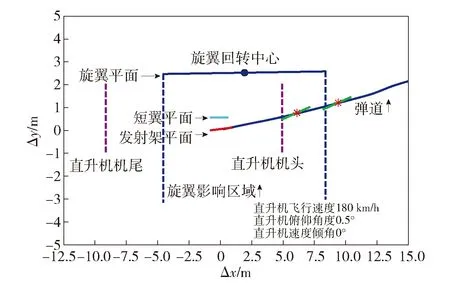
图13 直升机平飞攻击时机- 弹相对关系侧视图(飞行实验)Fig.13 Lateral view of the relationship between the helicopter and the missile during helicopter level flying (flight experiment)
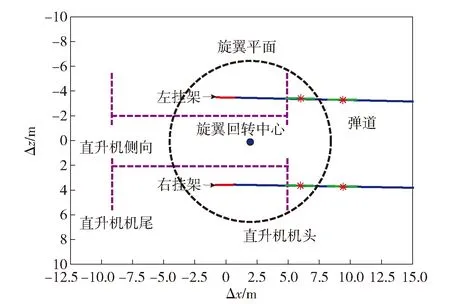
图14 直升机平飞攻击时机- 弹相对关系俯视图(飞行实验)Fig.14 Vertical view of the relationship between the helicopter and the missile during helicopter level flying (flight experiment)
2.3 发射安全性定量分析
在垂直方向上,即考虑导弹与旋翼的位置关系时,若满足以下条件,则导弹不会与直升机发生干涉:
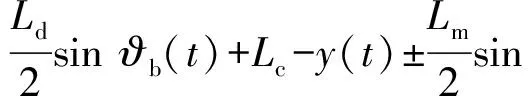
(1)
式中:y(t)表示导弹y轴方向位置随时间的变化量;ϑb(t)表示直升机俯仰角随时间的变化量;ϑ(t)表示导弹俯仰角随时间的变化量。(1)式中最后一项的正负号取决于导弹飞离旋翼时二者之间的几何关系。当导弹弹头离开旋翼时取负号;当导弹弹尾离开旋翼时取正号;t∈(0,tl)表示时间,tl为导弹飞离旋翼的时刻。
在水平方向上,即考虑导弹与直升机机体位置关系时,若满足以下条件,则导弹不会与直升机发生干涉:
(2)
式中:z(t)表示导弹z轴方向位置随时间的变化量,t∈(0,th),th为导弹弹尾飞离机头的时刻;ψ(t)表示导弹偏航角随时间的变化量。
不同直升机攻击模式下,导弹飞离机头时刻导弹与旋翼之间距离、导弹相对机体侧向位置以及飞离旋翼时刻导弹与旋翼之间距离的具体数值结果如表3所示。从表3中可以看出,不同的直升机攻击条件下,导弹与直升机的纵向、侧向均有足够的安全距离,导弹发射过程对直升机旋翼、机体不存在安全风险。
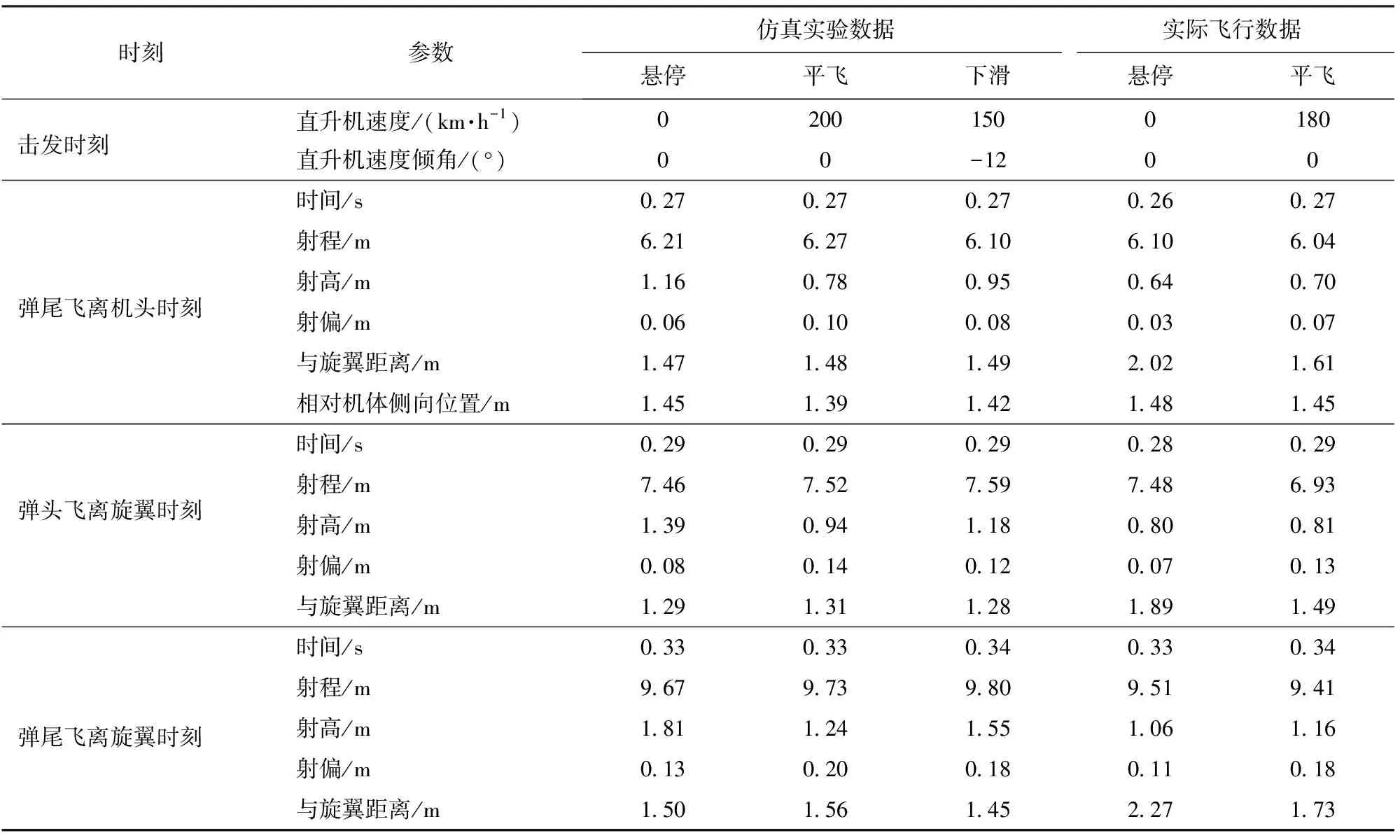
表3 不同攻击方式下发射安全性的实验结果Tab.3 Experimental results of launching security under different attacking modes
需要说明的是,本文给出的统计数值结果分别为导弹弹尾飞离机头时刻、导弹弹头飞离直升机旋翼以及导弹弹尾飞离直升机旋翼时刻3个特征点。为使安全性分析结果的余量更大,导弹飞离机头时刻是指导弹弹尾飞离机头的时刻,因为此时弹头距离直升机旋翼更近。
由表3可见,在空地导弹飞离直升机的过程中,导弹与旋翼的距离以及导弹与机体的距离均大于1 m,这些参数对横轴方向的距离量值影响较小,对分析空地导弹发射安全性的影响可以忽略;实际导弹发射飞行过程中,导弹与直升机之间的各距离参数数值更大,这是因为仿真实验时设置的条件较为苛刻,导弹的发射俯仰角和弹道扰动设置均大于导弹实际飞行情形。可见,合理的初始弹道设计和初始扰动抑制可有效提升空地导弹的发射安全性。
事实上,要想使安全性定量分析更严密,计算导弹与直升机之间发射安全性的几何关系时,还需要综合考虑弹翼最大外廓的范围以及导弹飞离直升机过程中的姿态角等参数。然而,这些参数的量值很小,此处予以忽略。
3 直升机旋翼下洗流对空地导弹初始弹道影响
3.1 下洗流对空地导弹初始弹道影响
当导弹处于下洗流区域时,在下洗流场的作用下,导弹飞行速度的大小和方向将产生变化,而导弹相对气流的攻角和侧滑角变化将会直接改变作用在导弹上的气动力和气动力矩。
直升机下洗流对导弹的影响可描述为在流场范围内,存在量值大小为vi,沿机体坐标系Obyb轴方向的风作用于导弹上(vi<0 m/s,表示下洗流场沿Obyb轴负方向),因此作用在导弹上相对来流的速度为导弹速度v和下洗流场速度vi的矢量差。下洗流场将带来附加的攻角和侧滑角。
将旋翼下洗后导弹相对于气流的速度用vr表示,则有
vr=v-vi,
(3)
下洗流场速度产生的原因在于,直升机旋翼下洗流场是一个涡流场,涡流在它周围会感应出速度场,称为诱导速度场,诱导速度是旋转的涡心通过黏性作用带动周围空气运动的速度,vi可通过工程计算或基于自由尾迹分析计算得到,洗流诱导速度是下洗诱导速度、切向诱导速度和径向诱导速度3个方向的流速矢量和[11-14]。
相对速度向量vr的模可表示为
(4)
式中:vx、vy、vz为地面坐标系中导弹质心运动速度在xe、ye、ze轴3个方向上的分量;vix、viy、viz为旋翼下洗速度在地面坐标系xe、ye、ze轴3个方向上的分量。
首先求解vix、viy、viz,Obxbybzb和Oexeyeze之间的关系由武装直升机的俯仰角、偏航角和滚转角确定,Oexeyeze至Obxbybzb的转换矩阵L(γb,ϑb,ψb)可表示为
(5)
因此,机体坐标系至地面坐标系的转换矩阵为L-1(γb,ϑb,ψb)。将沿机体坐标系的下洗速度vi转换至地面坐标系,即
(6)
由于旋转矩阵L(γb,ϑb,ψb)是一个正交矩阵,此旋转矩阵的逆和矩阵的转置相等,即L-1(γb,ϑb,ψb)=LT(γb,ϑb,ψb),L-1(γb,ϑb,ψb)表达式见(7)式。
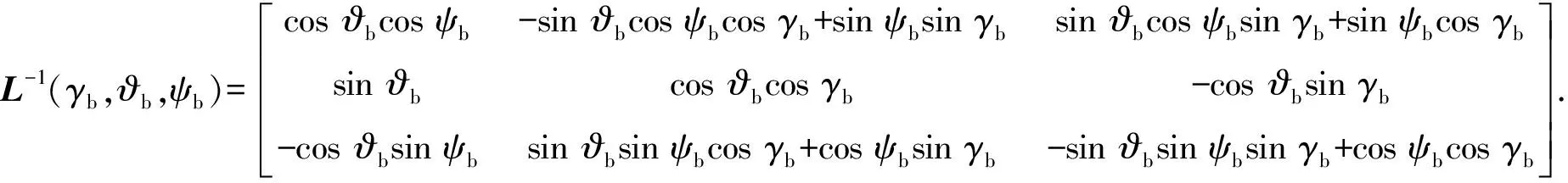
(7)
(7)式代入(6)式,可得
vix=(-sin ϑbcosψbcosγb+sinψbsinγb)·vi,
viy=cos ϑbcosγb·vi,
viz=(sin ϑbsinψbcosγb+cosψbsinγb)·vi.
(8)
进一步求解相对气流速度在Oxpypzp上的3个分量vrxp、vryp、vrzp,可以得到相对攻角αr和相对侧滑角βr.
为求vrxp、vryp、vrzp,重写(3)式,有
(9)
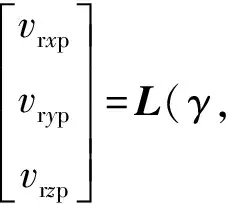
(10)
式中:L(γ,ϑ,ψ)的表达式形式与(5)式的旋转矩阵L(γb,ϑb,ψb)相同,仅下标不同。
根据(10)式可得相对气流速度在弹体坐标系上的3个分量,继而可以得到旋翼下洗条件下导弹的相对攻角αr和相对侧滑角βr:
(11)
当导弹飞越旋翼下洗流区域时,作用于导弹上的总空气动力和空气动力矩取决于vr、αr和βr.
来流坐标系下,气动力中的阻力Fxr、升力Fyr和侧向力Fzr可分别表示为
(12)
Fyr=Cy(αr,Ma)qrS,
(13)
Fzr=Cz(βr,Ma)qrS,
(14)
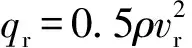
(15)
(16)
(17)
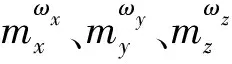
计算得到的气动力需要转换到Oxtytzt进行弹体运动学分析,各坐标系之间的关系如图15所示。
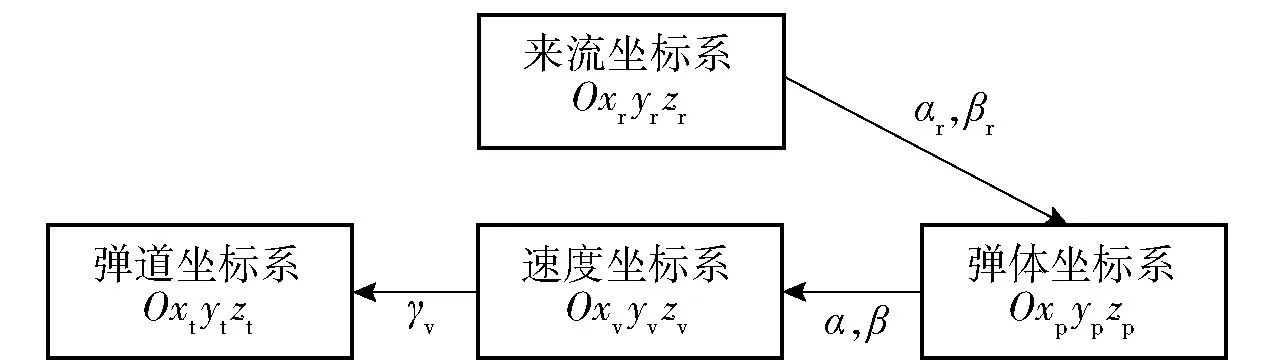
图15 坐标系之间的转换关系Fig.15 Transformation between coordinate systems
由图15可见,Oxryrzr和Oxpypzp之间的关系由相对攻角αr和相对侧滑角βr确定,Oxpypzp和Oxtytzt之间的关系由导弹攻角α、导弹侧滑角β和速度倾斜角γv确定。
因此,作用在导弹上的气动力[Fxr,Fyr,Fzr]T在Oxtytzt的投影[Fxrxt,Fyryt,Fzrzt]T可表示为
(18)
式中:

(19)
(20)
(21)
导弹飞离旋翼后,旋翼下洗流场对导弹不再有影响,即vi=0 m/s.将计算并转换得到的气动力和气动力矩代入导弹的六自由度运动方程[10],可以分析导弹在下洗流影响下的运动轨迹。
旋翼下洗流场对导弹发射的初始飞行状态和弹道轨迹的影响,主要表现在下洗流诱导速度场引起来流速度、攻角、侧滑角的变化,对导弹产生向下的俯仰干扰力矩,该力矩使得导弹抬头。
直升机下洗流场参数可通过工程计算、自由尾迹分析计算等方法获取[15]。某直升机旋翼典型下洗流速度的工程计算结果如图16所示,r表示旋翼平面中各点与旋翼中心的距离。由图16可见,下洗流速度从旋翼桨盘内侧向外侧逐渐增大,在接近旋翼边界时速度达到最大,然后迅速减小。

图16 直升机旋翼下洗流速度Fig.16 Down-wash flow speed of helicopter’s rotor
3.2 下洗流对空地导弹初始弹道影响仿真分析
以载机悬停攻击目标为例,仿真分析下洗流对空地导弹初始弹道的影响,俯仰姿态角、弹道倾角与y轴方向弹道曲线的实验结果分别如图17~图19所示。可见,在下洗流场的作用下,初始段导弹的俯仰姿态角ϑ有明显抬高,但此时导弹速度较低,对弹道影响较小。

图17 俯仰姿态角曲线Fig.17 Curves of pitching attitude angle

图18 弹道倾角曲线Fig.18 Curves of trajectory inclination angle

图19 弹道曲线Fig.19 Curves of missile trajectory
4 直升机飞行速度对导弹初始弹道的影响
通常而言,武装直升机的作战飞行速度小于等于200.0 km/h,直升机载空地导弹通常采用轨式发射形式。导弹离轨过程中,Δvm表示导弹的离轨初速,是发动机工作带来的速度增量。由于离轨过程中导弹仍与直升机固连,直升机的飞行速度带给导弹的速度分量为vb,速度倾角为θb,θ0为Δvm与Oxe轴之间的夹角。导弹离轨过程的速度vm为Δvm和vb的矢量和,即
vm=Δvm+vb.
(22)
根据几何关系及矢量相加原理,可以得到离轨过程导弹的速度大小vm和方向θ,可分别表示为
(23)
(24)
若直升机处于悬停状态,即vb=0 m/s,则导弹速度与Δvm一致。导弹离轨后姿态角不再受到发射架约束,直升机飞行速度对导弹不再有影响,导弹按六自由度运动规律飞行。
图20对比了不同直升机飞行速度下的导弹离轨过程,考虑两种直升机飞行速度vb1和vb2,直升机速度倾角均为θb,且vb2>vb1.
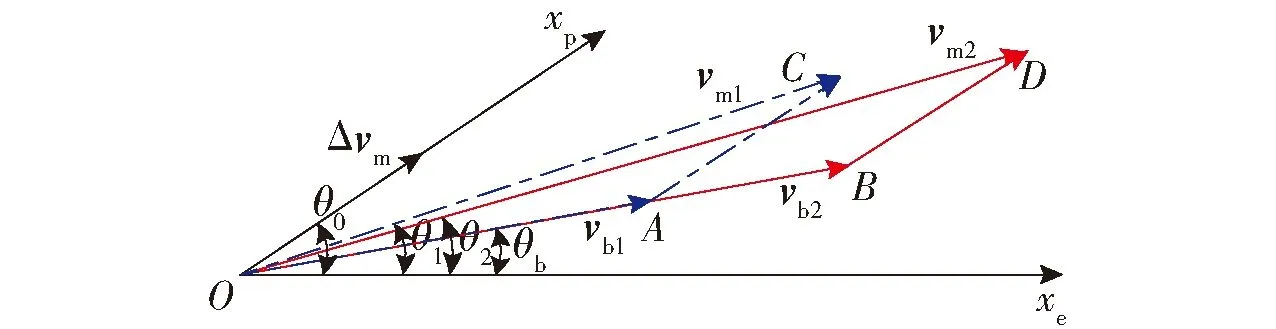
图20 导弹离轨过程的运动Fig.20 Motion of missile before leaving from launcher
图20中:在△OAC中,OA对应直升机的飞行速度带给导弹的速度分量vb1,AC对应导弹离轨初速Δvm,OC对应导弹离轨过程的速度vm1,弹道倾角为θ1=∠COxe;在△OBD中,OB对应直升机的飞行速度带给导弹的速度分量vb2,BD对应导弹离轨初速大小Δvm,OD对应导弹离轨过程的速度vm2,弹道倾角为θ2=∠DOxe;Δvm的大小由发动机工作特性和导轨长度等条件决定,不受载机特性的影响,即ACBD;当直升机飞行速度vb2>vb1时,对应的导弹离轨速度vm2>vm1,弹道倾角θ2<θ1;载机飞行速度越快,导弹离轨速度越大,离开载机区域的时间越短,且弹道爬行高度越低。
图21~图23给出了直升机不同飞行速度条件下的导弹速度、弹道倾角和y轴方向相对弹道曲线结果。仿真条件中待攻击目标位置位于(1 000 m,-50 m,0 m),直升机分别采用悬停攻击方式(此时直升机飞行速度为0 km/h)、平飞攻击方式(此时直升机飞行速度分别为100 km/h和200 km/h,速度倾角为0°)攻击目标。由图21可见,直升机飞行速度越快,导弹相应的离轨速度也越快。由图22可见,直升机飞行速度越快,则对应的弹道倾角越小。由图23可见,直升机飞行速度越高,导弹的初始弹道越低。
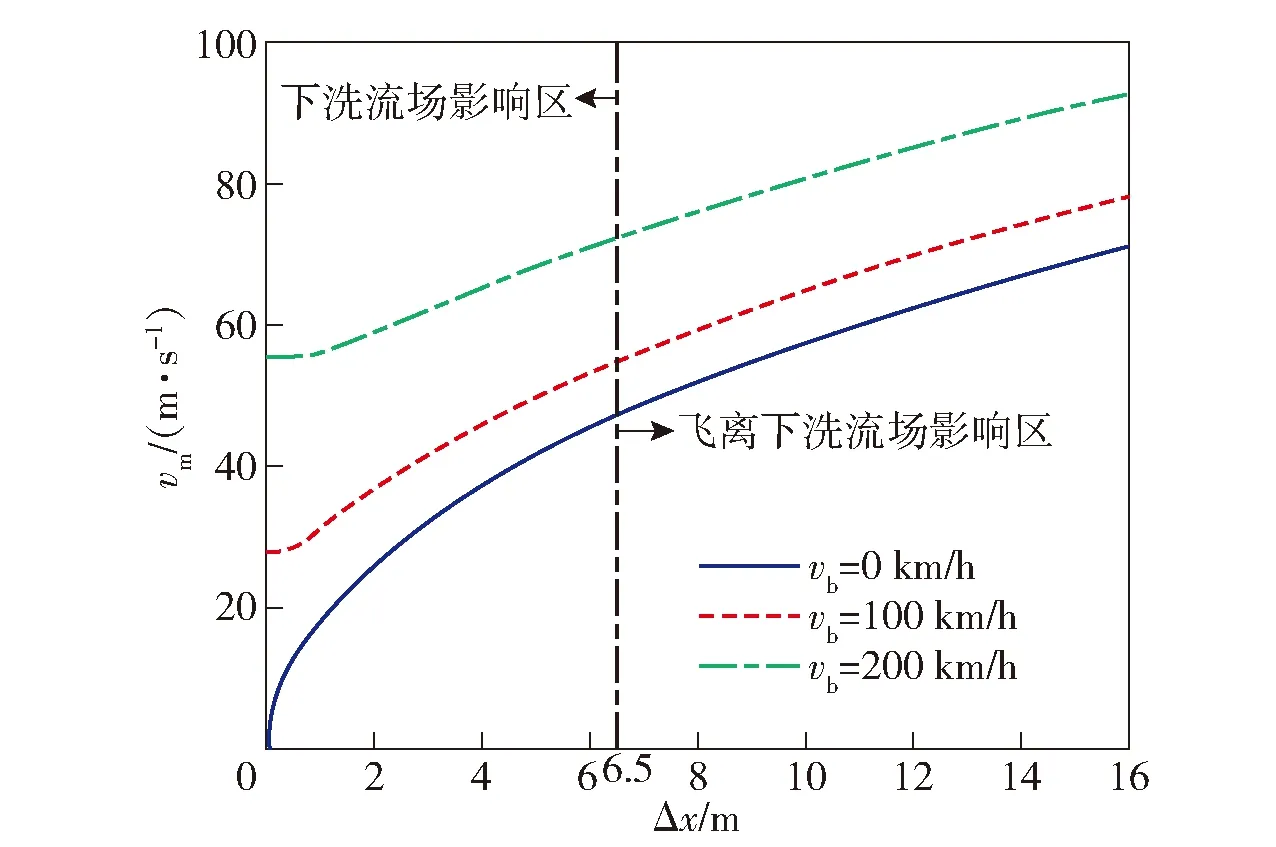
图21 不同直升机速度下的离轨速度曲线Fig.21 Curves of missile speed after leaving from launcher at different helicopter flight speeds
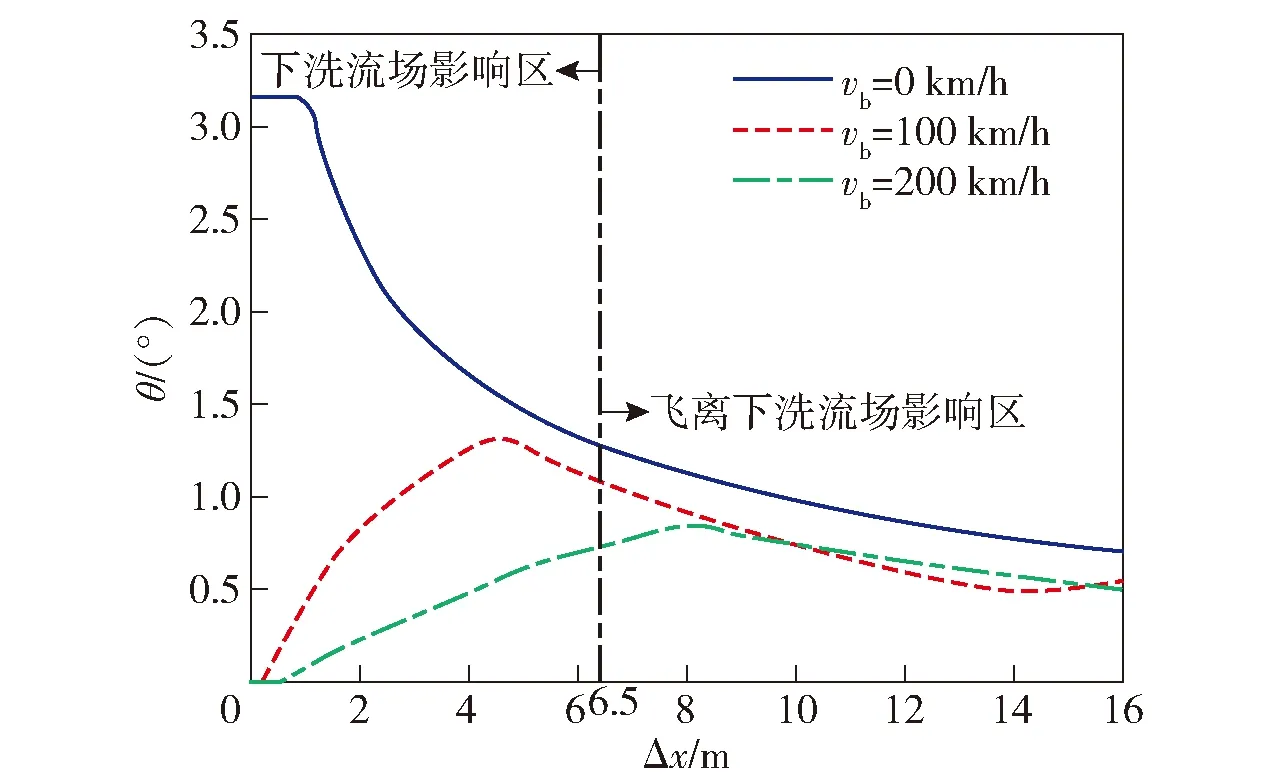
图22 不同直升机速度下的弹道倾角曲线Fig.22 Curves of trajectory inclination angle at different helicopter flight speeds

图23 不同直升机速度下的弹道高度曲线Fig.23 Curves of height of missile trajectory at different helicopter flight speeds
5 发动机喷流对直升机的影响
发动机喷流对直升机的影响主要体现在燃气和后喷物两个方面。为了获得较大的导弹离轨速度,通常采用初始大推力的发动机内弹道方案。初始大推力对应较高的初始工作压强(可达12~20 MPa)、较强的发动机喷流和较大的喷流影响区域。发动机喷流的流场建立过程很快,通常为毫秒级,此时导弹仍然在发射导轨上。导弹在发动机推力作用下向前运动直至离轨,发动机喷流及其影响区随之向前运动,高温燃气将不可避免地对直升机机体和发射导轨产生冲刷效应。此外,固体发动机喷流中通常含有固相喷出物。固相喷出物随高温燃气流喷出,可能与直升机的机体和发射导轨发生碰撞。
分析发动机喷流对直升机影响的流程图如图24所示,其核心在于通过数值仿真或试验获得可靠的发动机尾流场数据,从而分析其影响区域,同时考虑两相流效应,获得喷出物的大致运动轨迹。
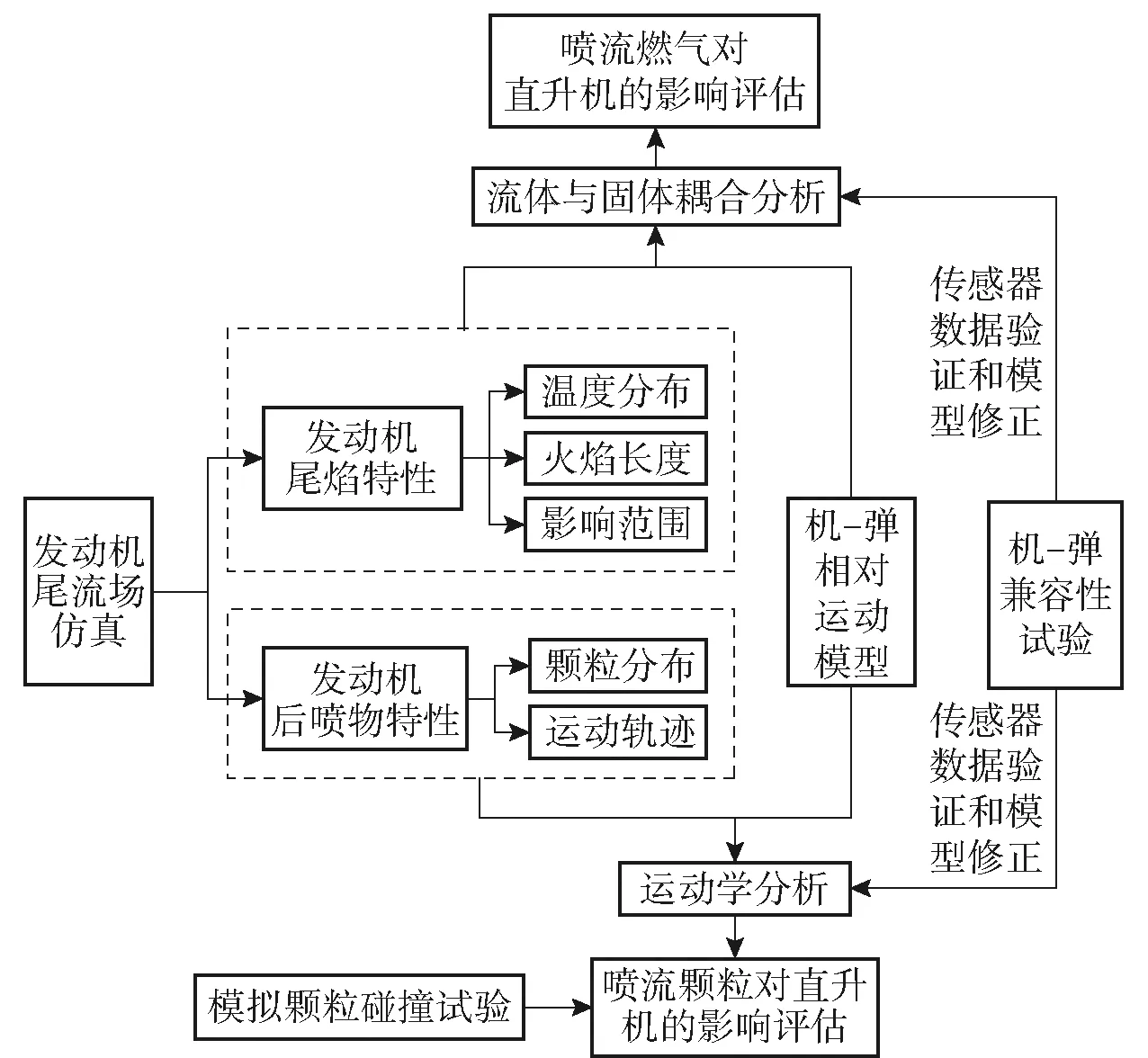
图24 发动机喷流对直升机的影响分析流程图Fig.24 Analysis process of the influence of SRM plume on helicopter
图24中的流体与固体耦合分析综合机弹相对运动模型和发动机尾焰特性开展,目的是进行喷流燃气对直升机的影响评估。运动学分析则是综合机弹相对运动模型和发动机后喷物特性开展,目的是进行喷流颗粒对直升机的影响评估;机弹相容性试验通过试验来验证流体与固体耦合分析和运动学分析。
以某型空地导弹为例,应用Fluent软件对发动机尾流场进行建模仿真,其射流方向的温度分布曲线(即发动机喷管轴线上的温度分布)如图25所示。
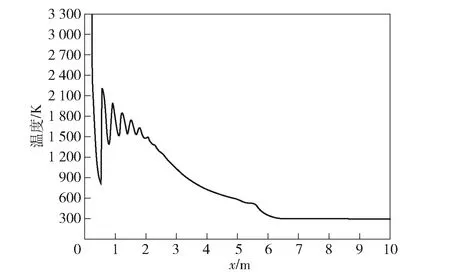
图25 发动机喷管轴线上的温度分布Fig.25 Temperature distribution along the axis of SRM nozzle
由图25可见,发动机后喷燃气的能量主要集中在轴线附近,其温度和速度沿径向均衰减很快。以温度900 K来判断火焰长度,则该稳态流场的火焰长度约为3.3 m,半径方向最大影响范围约0.2 m.
发动机喷流影响区域固连于导弹尾部,进行导弹与直升机相对运动过程仿真(此处忽略发动机喷流影响区域的建立过程和波动)和发动机喷流影响区域与直升机机体的干涉分析,可以获得发动机喷流对直升机的机体和发射导轨的影响区域和作用时间。结合流体- 固体耦合仿真,还可以获得直升机的机体和发射导轨局部的温度场信息,判断可能的烧蚀风险点。发动机喷流与直升机位置关系如图26所示。

图26 发动机喷流与直升机位置关系示意图Fig.26 Relative position between the helicopter and the plume of SRM
在尾流场仿真的同时,在入口加入颗粒相喷出物,考虑流场和颗粒的单向耦合,可获得典型的颗粒运动轨迹。发动机喷流中的喷出物信息可以通过地面试验收集后方喷出物测量并统计获得,也可以通过高速电荷耦合器件相机和激光器搭建粒子成像测速测量系统获得[16]。进行导弹运动过程中颗粒轨迹和直升机机体的干涉分析,可获得喷出物与直升机机体和发射导轨的碰撞点和碰撞时的颗粒速度、方位信息。通过气压或者机械驱动试验装置发射不同数量颗粒直接碰撞直升机机体蒙皮或发射导轨,设计不同时长的考核试验,即可分析评估单个喷出物单次、多次或者持续碰撞对直升机机体和发射导轨的影响。
事实上,针对发动机喷流与后喷物的数值模拟和试验手段都存在一定误差,很难定量描述其对直升机的影响。因此实际导弹研制过程中,通常需要进行试验弹挂载发射的机- 弹相容性实验来验证其对载机的真实影响。某空地导弹的真实发动机点火机- 弹相容性实验如图27所示。在机- 弹相容性实验中,在直升机机体和发射导轨特征位置布置多组压力和温度传感器,可获得特征位置的相关流场和颗粒信息。将测量信息用于数值仿真模型的验证和修正,可为后续数值仿真分析与设计优化奠定基础。

图27 发动机点火机- 弹相容性实验Fig.27 Compatibility experiment of helicopter and missile during SRM firing
6 结论
本文结合空地导弹在直升机攻击条件下的飞行特性,从直升机旋翼下洗气流对初始弹道的影响、直升机飞行速度对初始弹道的影响、导弹发射过程中导弹初始弹道与直升机的相对位置关系、发动机喷流对武装直升机的影响等多角度,对武装直升机和空地导弹的机- 弹相容性进行了较全面的系统分析。所得主要结论如下:
1)直升机下洗流速度会给空地导弹的初始弹道带来俯仰抬头的干扰力矩,初始段导弹姿态角会有上抬现象,但由于导弹的初始速度偏低,对弹道的影响较小。
2)不同的直升机飞行速度会对空地导弹的初始弹道产生影响,直升机飞行速度越大,初始弹道越低。
3)发动机尾焰对直升机的影响可通过仿真分析与外场试验相结合的方式进行。
此外,结合武装直升机和导弹的相对位置关系,对发射安全性进行了详细建模,实验结果表明,严苛条件下,空地导弹的初始弹道与直升机的纵向、侧向均有足够的安全距离,导弹发射对直升机旋翼、机体不存在安全风险。本文方法可为直升机载空地导弹机弹相容性设计、攻击条件选择等提供有力的技术支持。

