旋转稳定弹扰流片气动外形多目标优化设计

钱龙， 常思江， 倪旖

(1.南京理工大学 能源与动力工程学院， 江苏 南京 210094； 2.上海机电工程研究所， 上海 201109)

0 引言

微型扰流片作为一种新型二维修正弹的气动执行机构，具有结构简单、执行动作简捷、成本较低、可提供持续控制力等优势，近年来备受关注[1-5]。大量研究结果表明，扰流片控制力作用于弹箭尾端的气动布局在旋转稳定弹上的控制效果，比控制力作用在弹丸前端的鸭式布局优势更加突出[6-10]。Fresconi等[3]利用六自由度弹道模型验证了用扰流片实现弹道修正的可行性，结果表明，采用扰流片控制力作用于弹箭尾端气动布局的旋转稳定修正弹弹道，其修正范围大于弹道散布且飞行稳定。法国国防部为专门研究旋转稳定弹的二维修正技术，设立了一个名为MANEGE的项目，Wey等[5]将扰流片气动执行机构应用于155 mm弹丸，对不同初速、射角下的修正能力进行研究，发现在一定射击条件(不同初速、不同射角)下在弹道末端激活扰流片即可使修正距离大于无控散布范围。Arnoult等[11]对该类气动布局的旋转稳定修正弹进行了3个马赫数Ma点的风洞实验，提出采用多可信度代理模型的Co-Kriging模型，将少量风洞数据作为扰流片气动系数的高可信度评估、大量的计算流体力学(CFD)方法数据作为低可信度评估，二者结合可提高修正弹扰流片气动力参数的计算速度和精度。

以上文献表明采用微型扰流片的气动布局能够有效提高旋转稳定修正弹的修正控制能力，但其几何外形依赖性即扰流片气动外形对修正弹修正能力及弹道的影响规律有待深入分析。文献[12-13]提出采用Kriging模型和人工神经网络作为气动力系数的代理模型，指出在给定扰流片激活时间后即可确定其最优结构。但文献中定义的优化目标函数较为单一(仅弹道修正量)，并没有给出具体的扰流片气动力以及优化后的具体弹道结果，如修正距离、落点速度等诸元。此外，文献[5，11-13]设计的扰流片都为小段圆环外形，没有具体对扰流片外形形态及其作用机理进行探究。在国内，钱龙等[14]、杨杰等[15-16]针对带扰流片旋转稳定弹初步开展了气动特性分析、外弹道建模仿真以及制导律设计等研究，但并未涉及扰流片外形设计问题。

本文以带微型扰流片的某旋转稳定弹为研究对象，通过研究其弹道修正机理建立以扰流片外形参数为设计变量、以弹道修正量和终点存速为优化目标，并考虑攻角、修正能力及扰流片尺寸约束的多目标优化设计数学模型，通过联立前馈神经网络气动响应模型和有控刚体弹道模型获得设计变量和目标函数之间的关系，并采用遗传算法获得全局最优解。与文献[12-13]相比，本文研究在3个方面有所改进：1)除弹道修正量外，增加终点存速这一重要弹道性能为目标函数；2)给出了亚声速、跨声速、超声速条件下弹丸的升阻比函数形态；3)对扰流片作用下弹丸的姿态变化及升阻特性进行了机理分析。本文研究结果可为该类旋转稳定修正弹的设计与研制提供一定的参考。

1 外弹道特性

1.1 扰流片弹道修正机理

本文安装扰流片的思想主要如下：将旋转稳定弹简易改造后通过紧固螺纹连接后体控制舱，修正弹前体外形与原无控弹弹型无异，后体(船尾)上安装有扰流片控制组件，如图1所示。控制舱内配备有对扰流片机构进行动作控制所需的控制系统，如滚动轴承、减速反旋电机、滑轨机构等。轴承体带有螺纹连接前后体，可差动旋转。有控弹道段后体反旋电机与刹车片使后体减旋直至相对弹轴坐标系静止，扰流片使弹体两侧产生非对称气动力，为弹体提供侧向力。在扰流片和滚转角控制器的共同作用下，完成旋转稳定弹的姿态调整、弹道修正。该修正弹打击范围广、反应快速、控制效率较高、修正能力较大，此外没有大面积弹翼、依靠陀螺稳定是其重要特征。

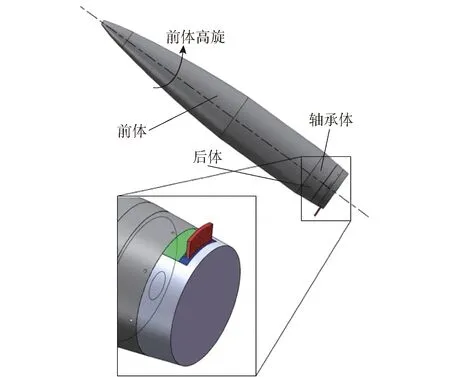
图1 带微型扰流片修正弹控制系统原理示意图Fig.1 Schematic diagram of control system for correction projectile with microspoiler

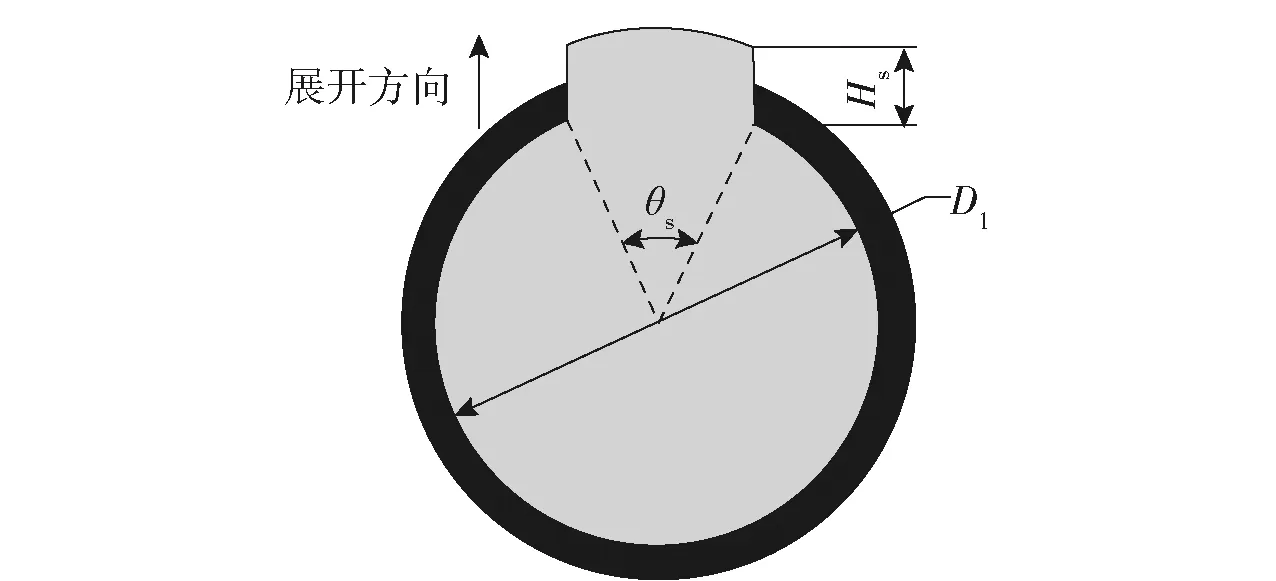
图2 扰流片外形示意图Fig.2 Outside view of microspoiler

该扰流片面积Ss的计算公式如下：

(1)

1.2 弹道特性

扰流片张开后，弹体随即产生附加的气动力和力矩，飞行姿态发生变化，进而实现弹道修正。这一过程如图3所示。图3中，Oξ、Oζ、Oη分别为弹轴坐标系的3个坐标轴；As、Ms、Ns分别为扰流片产生的轴向力、俯仰力矩以及法向力；Nb为弹体法向力；δM0为平衡攻角；序号①、②、③、④分别表示扰流片弹出、弹轴发生摆动、速度轴稳定、弹轴摆动收敛，反映了弹体的动态变化过程。

图3 微型扰流片引起弹丸姿态变化的示意图Fig.3 Change of projectile attitude caused by microspoiler

由图3可见，在扰流片作用下，旋转稳定弹丸弹道特性的变化可描述如下：

1)扰流片打开后，其位置与弹轴坐标系保持相对静止。扰流片组件与前弹体隔转，但随前体作章动、进动运动。扰流片产生的2个附加力(作用点在弹轴上，即已将实际扰流片产生的附加力等效至弹轴上)中仅Ns会对弹丸形成力矩，即图3中的力矩Ms.

2)旋转稳定弹的陀螺效应使得弹丸头部向右偏转(假设该旋转稳定弹为右旋弹)。

3)在扰流片和弹体共同的气动作用下，弹丸作幅值和频率为时变的二圆运动，且该角运动特性与飞行工况、扰流片张开情形(如弧长、高度、位置)都有关。

4)经一段时间后，弹体接近稳定于新的平衡状态，攻角趋于一个稳定值。

2 气动特性

2.1 数值验证

采用CFD方法计算修正弹有控以及无控时全弹气动特性。控制方程为雷诺平均Navier-Stokes方程，空间无黏通量采用ROE-FDS格式离散，黏性通量采用2阶迎风差分格式离散，时间项采用隐式LU-SGS算法，单元体中心处结果变量的梯度计算采用基于单元体最小二乘法。为加快数值计算的收敛速度，采用多重网格初始化技术。湍流模型采用两方程Realizablek-ε模型。

为了验证上述数值方法，对文献[17]中的M910弹丸进行数值计算，并将结果与文献[17]中的实验数据进行对比，如图4所示。图4中，CD为阻力系数，CNα为法向力系数导数。

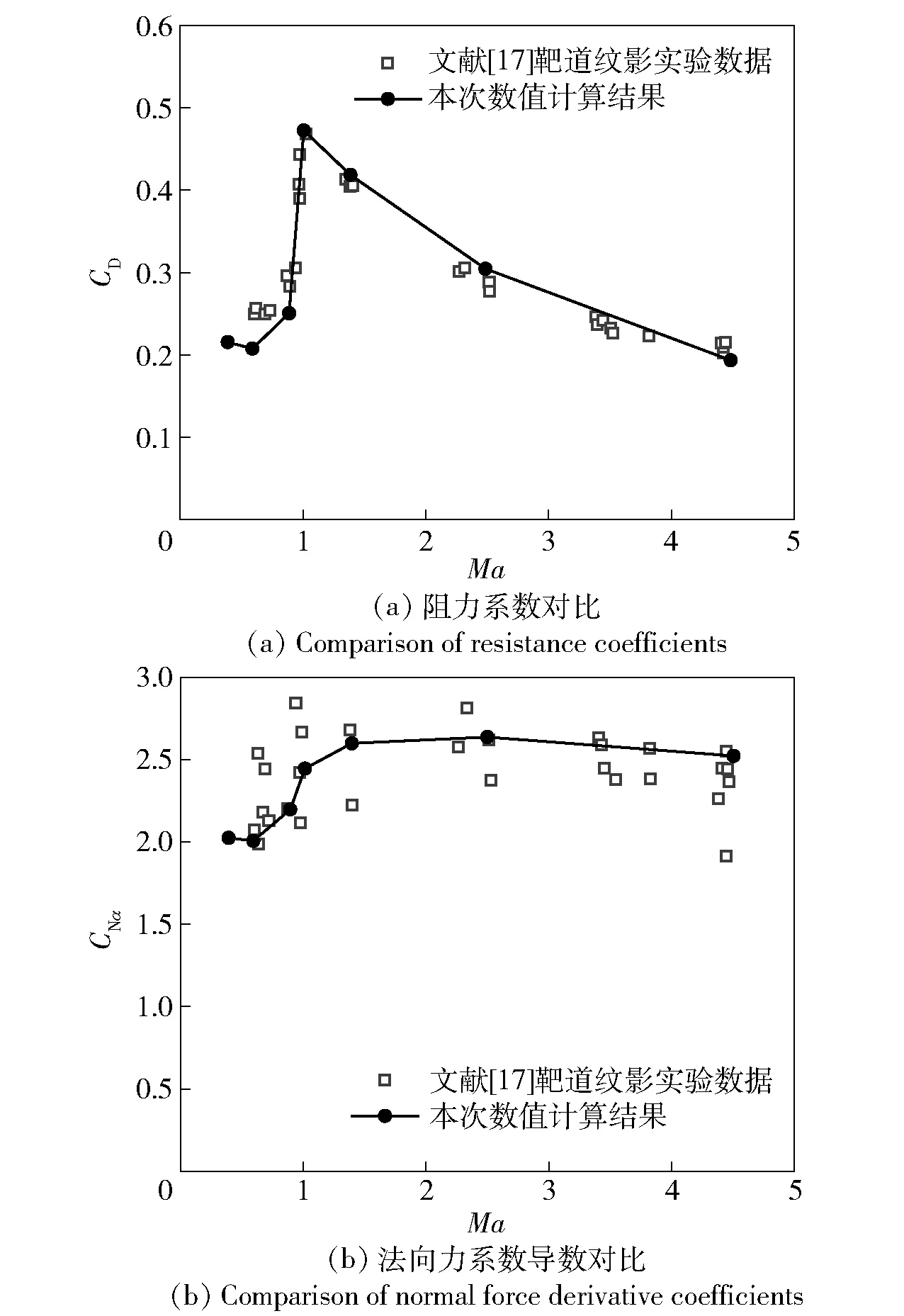
图4 气动系数数值计算与文献[17]实验结果对比Fig.4 Comparison of calculated result and experimental result in Ref.[17] of aerodynamic coefficient

由图4可知，上述数值方法具有较好的精度，采用该方法计算加装扰流片后修正弹的气动特性，可分析在不同扰流片外形参数和攻角- 扰流相位姿态下所受气动力的变化。气动特性数值计算时，取Ma分别为0.50、0.80、0.95、1.20及1.50，涵盖亚声速、跨声速、超声速范围。

2.2 弹体姿态的扰流影响分析

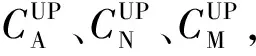
(2)

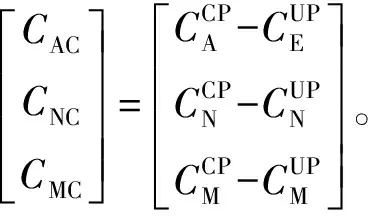
带微型扰流片弹丸所受力矩状态如图5所示。图5中，X轴为气流方向，Y轴为静力矩的反方向，Z轴与X轴、Y轴构成左手坐标系，M表示静力矩，RA、RN分别为轴向力和法向力，ΔRA、ΔRN分别为扰流片引起的附加轴向力和法向力，ΔM为扰流片产生的附加力矩。

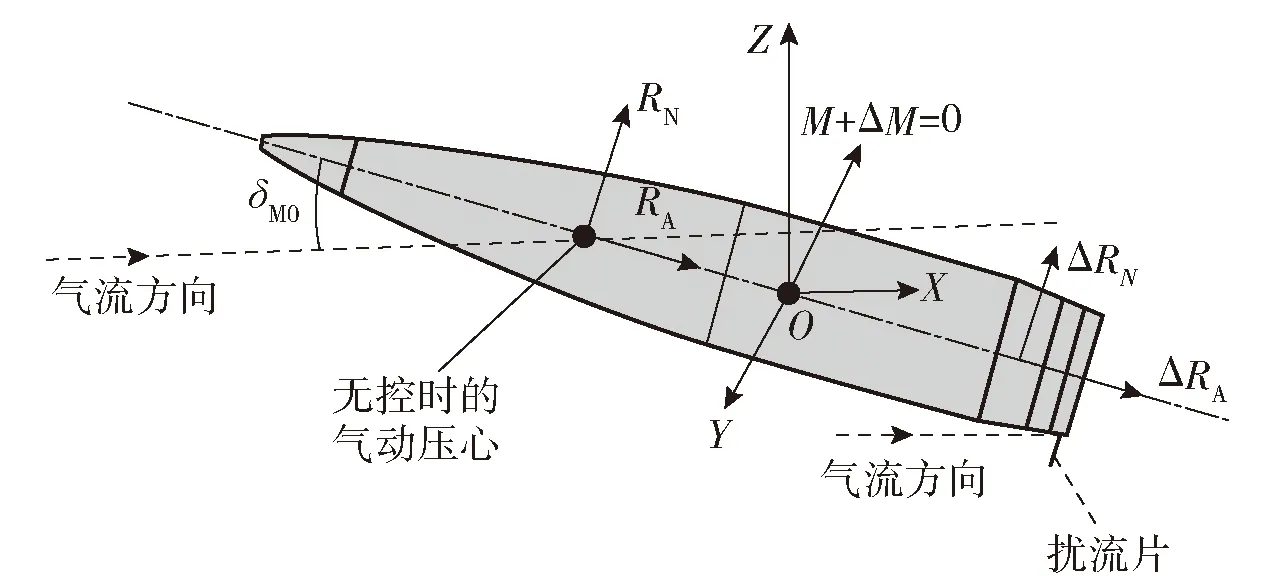
图5 弹丸所受气动力矩示意图Fig.5 Schematic diagram of aerodynamic moment of projectile

由图5可见，攻角面OXZ中，当扰流片向下打开时，扰流产生的附加力靠近弹底指向右上方，此时扰流片法向力系数CNC>0、扰流片静力矩系数CMC<0.由于旋转稳定弹丸的压心位于质心前，只有攻角增大到δM0时静力矩才为0 N·m，而此时CNC>0，故附加法向力与前弹体所受法向力方向一致，称其为法向力叠加效应。全弹的法向力主要与平衡攻角δM0以及附加的扰流片法向力有关，即与CMC、CNC有关。

以Ma=0.50、δ=4°工况为例，采用初始扰流片外形得出的弹丸纵向截面压力分布图如图6所示。

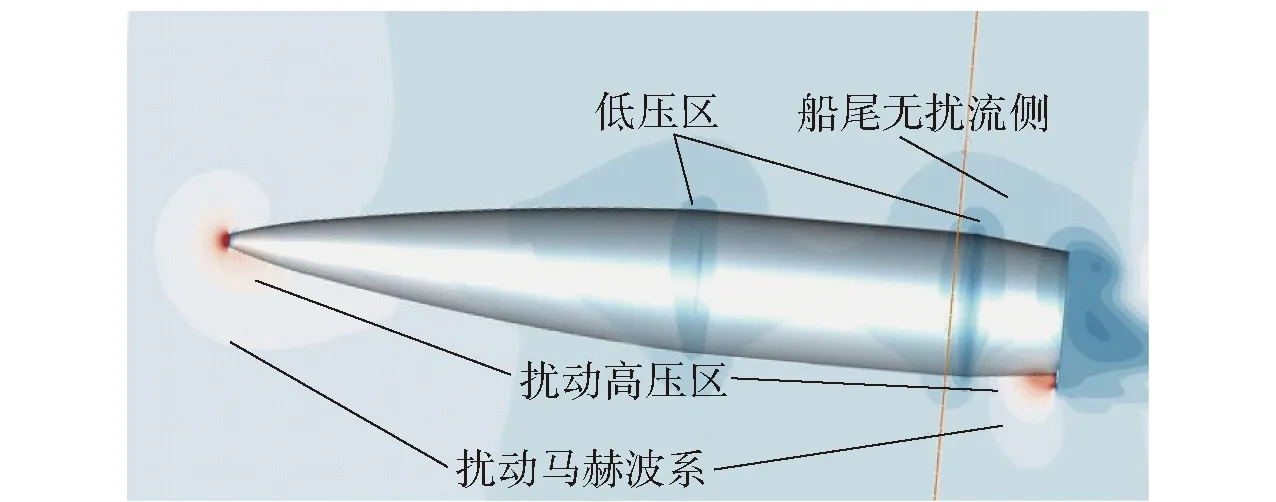
图6 修正弹周围纵向截面压力分布示意Fig.6 Pressure distribution of longitudinal section around correction projectile

从图6中可以看出：扰流片能够有效改变流场结构，提高弹尾处一侧的压力，从而增加弹体法向力；当保持扰流片其余外形参数不变，增加其高度或弧长，可提高CNC与CMC的数值，继而增大平衡攻角δM0.

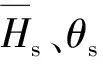
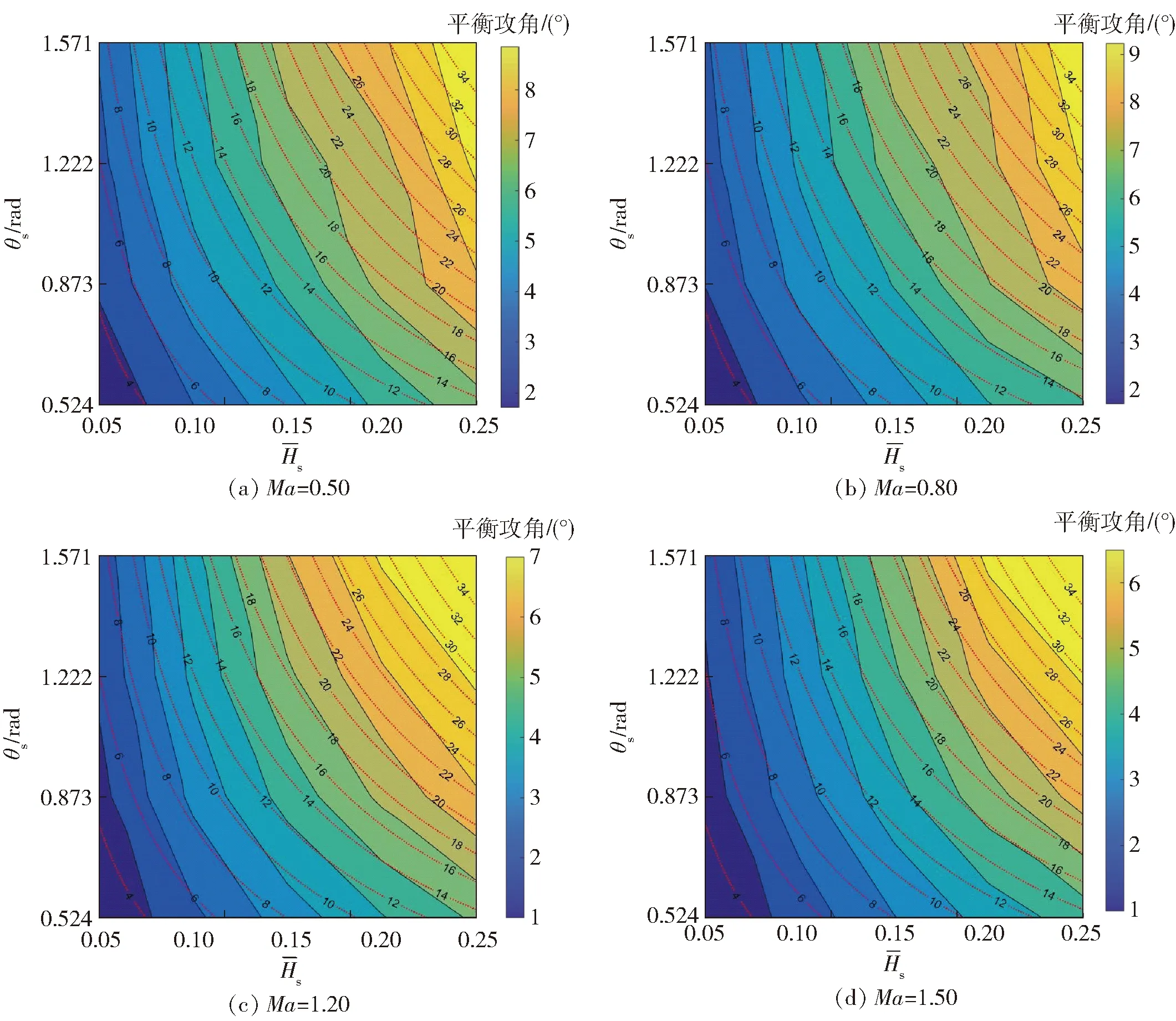
图7 各Ma下δM0随参数的变化(图中数据为扰流片面积，单位为cm2)Fig.7 δM0 vs. at various Mach numbers (the data in Fig.7 expresses the area of spoiler, unit: cm2)

2.3 新平衡态下升阻比分析

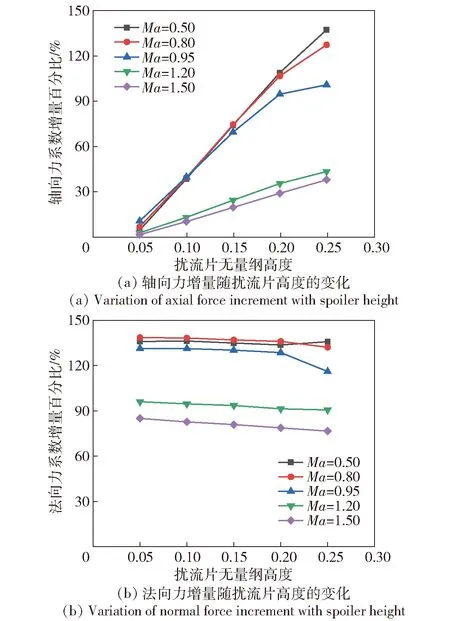
图8 扰流片高度变化对气动力的影响Fig.8 Influence of spoiler height on aerodynamic force

从图8中可以看出：随着扰流片高度增加，全弹轴向力系数增量呈递增趋势，总体随Ma增大而减小，变化范围随着Ma升高而缩小；全弹法向力系数增量基本不随扰流片高度变化而变化，其随Ma增大而略有减小。值得注意的是，扰流片引起的全弹法向力系数增量ΔCN较大：当Ma=1.50时ΔCN≈80%，当Ma=0.50时ΔCN≈130%，且低Ma下扰流片带来的附加法向力系数增量更可观。可见在Ma取值为0.50、0.80、0.95时，随着扰流片高度增加，全弹轴向力增加速度接近全弹法向力增加速度，从本文后续分析可以看到，虽然更大的扰流片面积产生的δM0更大，能够产生更大的弹体升力，但δM0带来的诱导阻力也将更大，故应当考虑在扰流片尺寸增加适当、有限的阻力下，利用扰流片来提升附加法向力，即关注该扰流片升阻比随扰流片外形参数的变化。

图9所示为修正弹的升阻比(CL/CD，CL为升力系数)随扰流片高度的变化曲线。

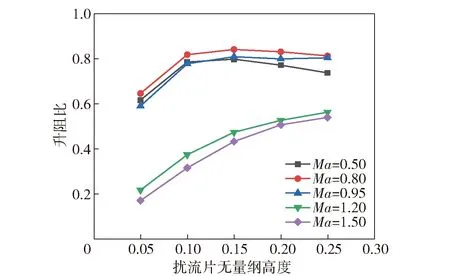
图9 升阻比随扰流片高度变化曲线(θs=0.523 rad)Fig.9 Variation of lift drag ratio with spoiler height(θs=0.523 rad)

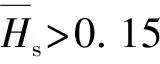
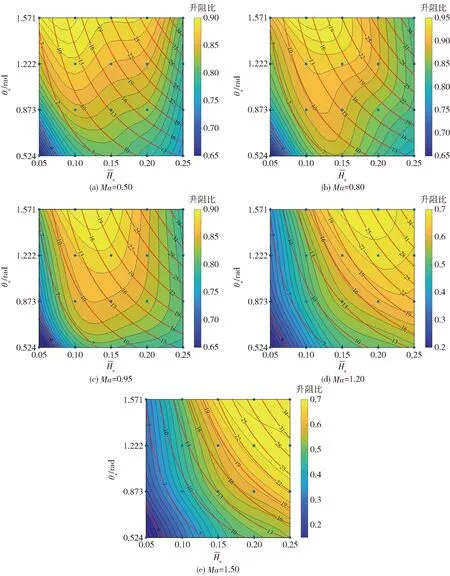
图10 升阻比随参数θs和变化(图中数据为扰流片面积，单位为cm2)Fig.10 Variation of lift drag ratio with variables θs and (the data in Fig.10 expresses the area of spoiler, unit: cm2)

3 优化模型建立与求解

3.1 基于响应面与CFD方法相结合的优化流程

直接采用基于CFD方法的优化迭代方法耗时较长，故本文考虑构建扰流片外形参数至气动参数的响应面(即代理模型)，保证在一定精度条件下能快速获取扰流片气动系数，结合弹道解算、目标函数计算、算法寻优、外形更新设计，最终获得优良的弹道性能以及相应最优气动外形，优化流程如图11所示。

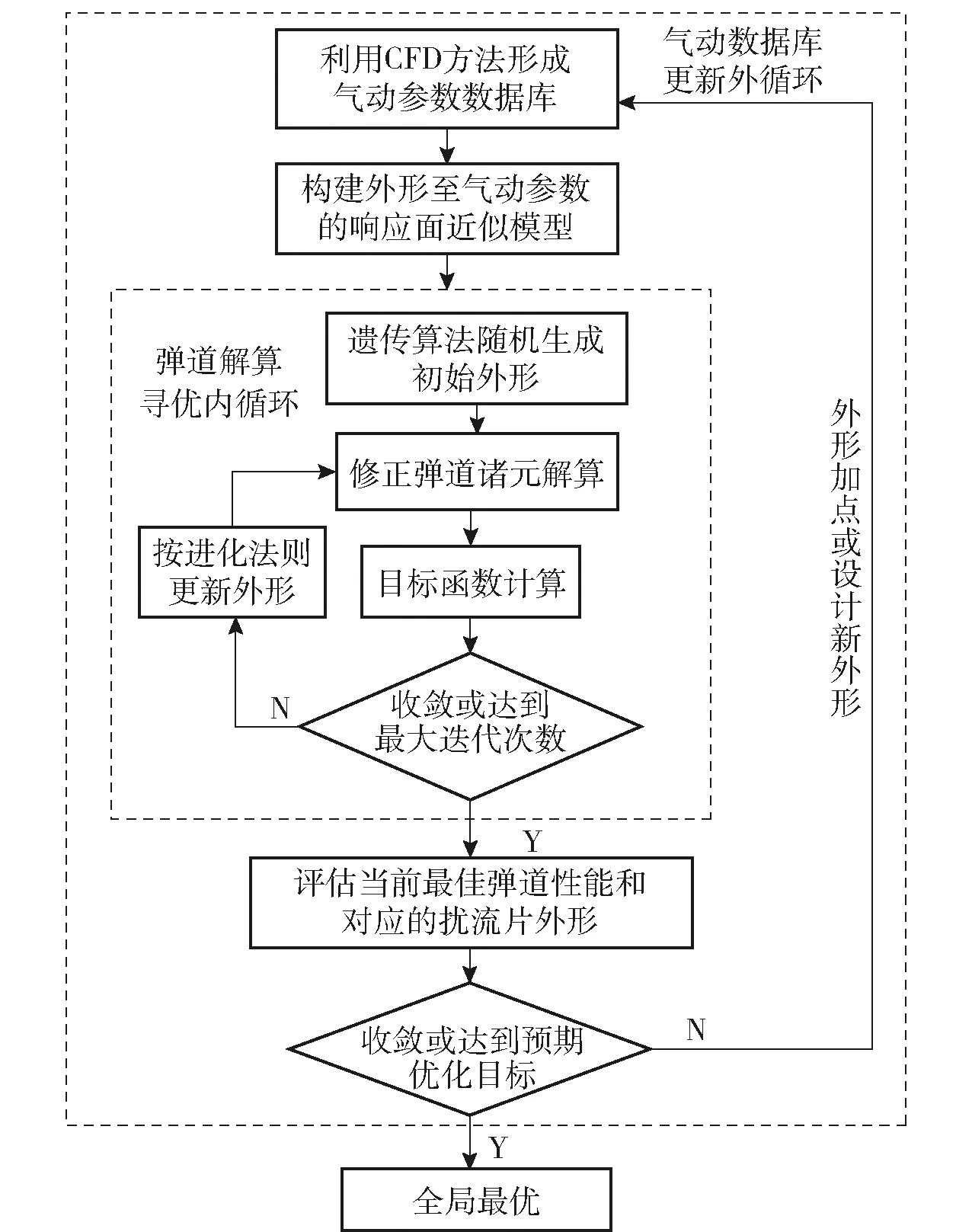
图11 优化流程图Fig.11 Optimization flow chart

本文的气动计算以CFD方法为基础，构建基于前馈神经网络的气动力预测模型作为其代理模型，以保证寻优时的计算速度。CFD数值模拟方法经过大量计算验证可保证较高精度[14]。文献[12]采用的多层感知器神经网络本质上即为前馈网络的一种，其采用最速梯度下降法来训练网络权阈值，收敛速度较慢，易陷入局部最优。为提高神经网络训练的全局寻优能力和收敛速度，本文选用自适应遗传算法训练网络权阈值。

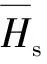
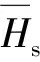
与图7的线性插值结果相比，图12所示神经网络预测的δM0精度较高，其响应面光滑程度与实际函数的光滑特性相符，可供有控弹道计算。

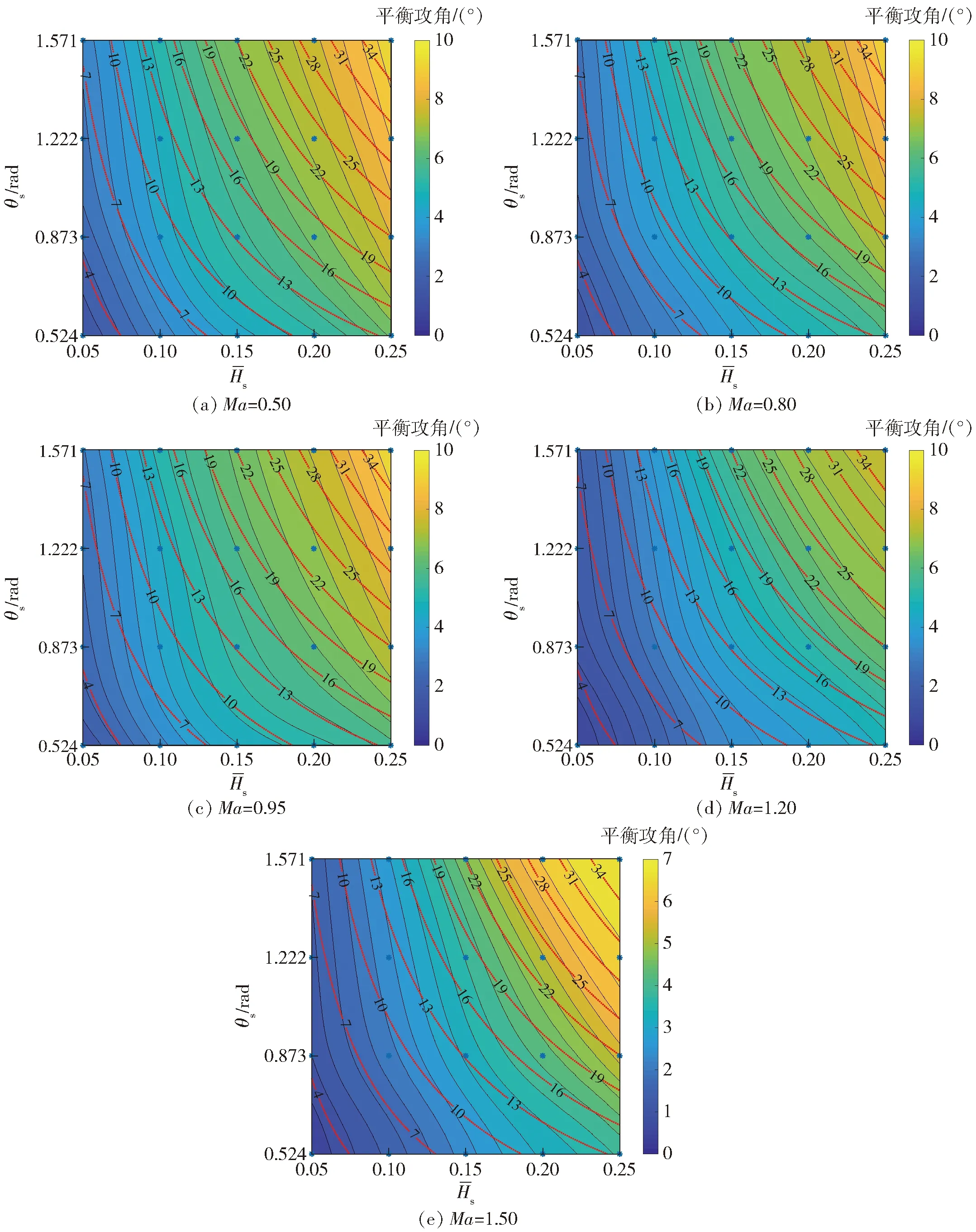
图12 神经网络预测δM0随的变化(图中数据为扰流片面积单位为cm2)Fig.12 δM0 vs. and θs (the data in Fig.12 expresses the area of spoiler, unit: cm2)

3.2 设计变量、约束函数与目标函数

经综合考量，设计如下目标函数：

(3)

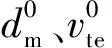
考虑修正弹弹道性能要求、扰流片外形特点，优化时应该满足以下约束条件：

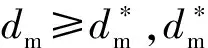
3)扰流片尺寸约束。由于在修正弹无控段，扰流片收纳在控制舱内，控制舱的体积、滑轨结构、擒纵机构等都对扰流片提出了尺寸限制要求。图13所示为扰流片尺寸限制与控制舱直径关系。图13中，D*为控制舱内可用直径，Ws为扰流片的弧长。

由图13可知：从设计角度，扰流片的外形不宜过大，在控制舱容积内扰流片高度和弧长相互制约，弧长越小，扰流片可弹出高度越大，弧长越大，扰流片可弹出高度越小，即一定弧长下有扰流片高度的边界值；滑轨结构和擒纵机构的设计对扰流片的高度和弧长上界提出了限制。故本文设计变量的约束条件如下：

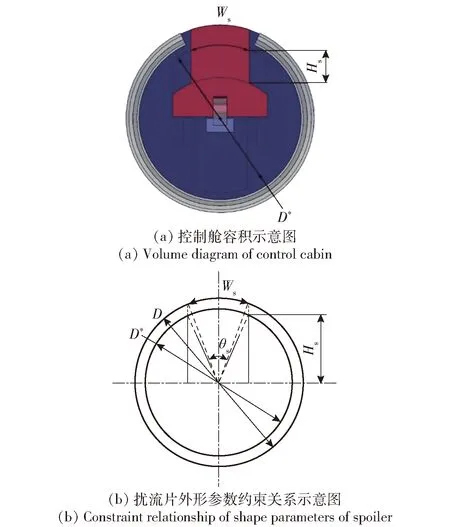
图13 扰流片尺寸限制与控制舱直径关系示意图Fig.13 Relationship between spoiler size limit and control cabin diameter

(4)

3.3 设计变量与目标函数、约束函数的联系

该优化设计模型属于有约束的非线性规划问题，优化设计变量与目标函数、约束函数之间没有显式的函数关系式。根据图11所示优化流程，本文利用CFD方法获得一定数量(3.1节所述不同条件)的扰流片气动力系数，据此离线训练出较为精确的神经网络代理模型。在优化过程中，该代理模型的输入为扰流片外形参数，输出为相应的扰流片气动力系数CAC、CNC、CMC，直接将其代入计及扰流片作用的有控弹道方程组[15]中进行弹道计算，可得到弹道修正量、终点速度、攻角等与目标函数、约束函数相关的参量。在寻优过程中，需要反复进行气动力和弹道计算，必须时刻满足设计变量的范围约束、弹道诸元的状态变量约束。

3.4 优化模型的求解方法

为了获得优化设计数学模型的全局最优解，避免陷入局部最优，本文采用全局搜索能力较强的遗传算法，在生成种群以及变异的过程中给予设计变量的边界约束，而在计算目标函数的时候对超出状态变量约束的个体给予一定惩罚，经过不断地迭代进化产生较好的种群和个体，最后找出最优或较优解。

3.5 优化结果与分析

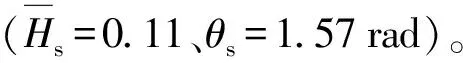
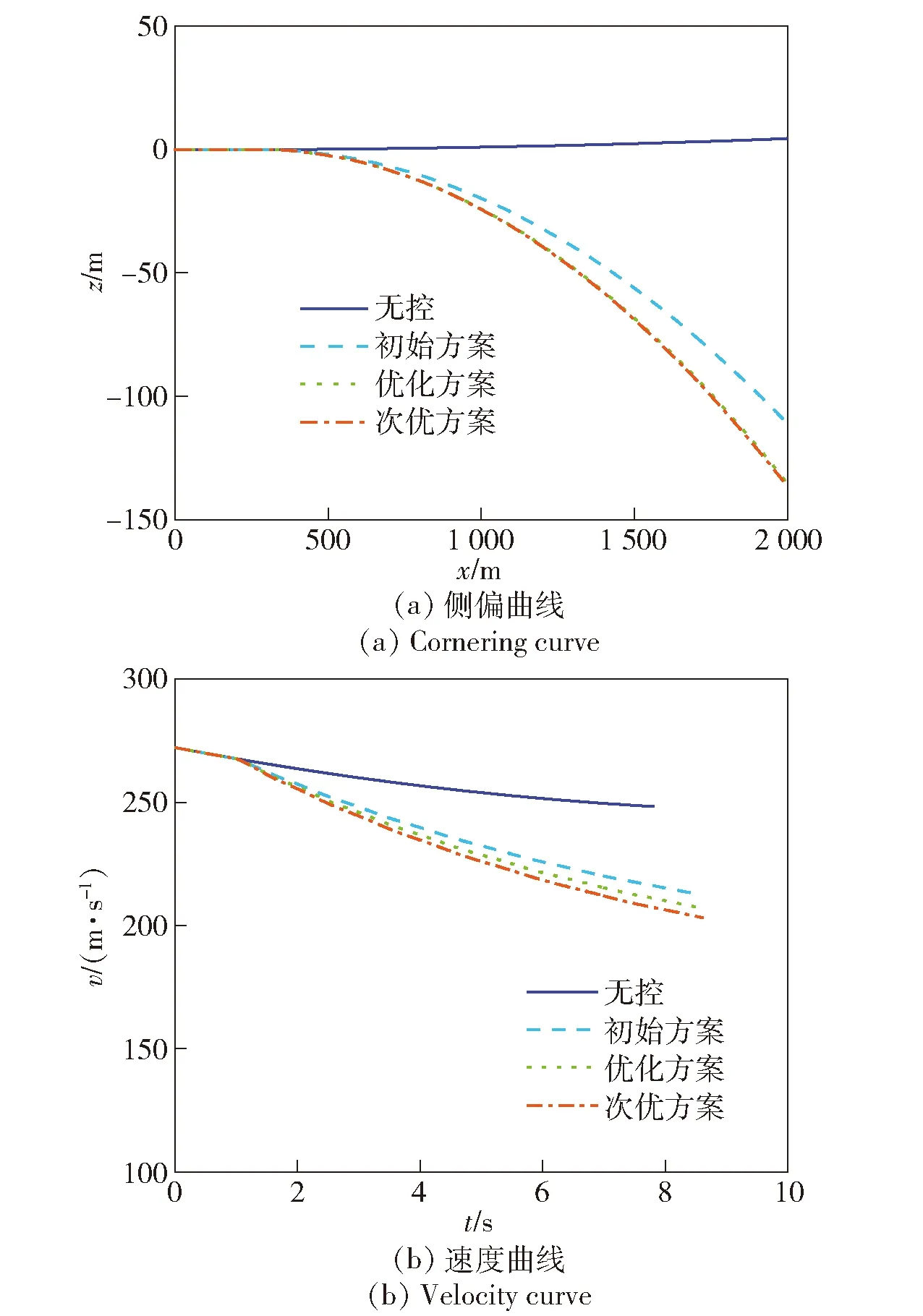
图14 优化前后弹道对比曲线Fig.14 Trajectory curves before and after optimization

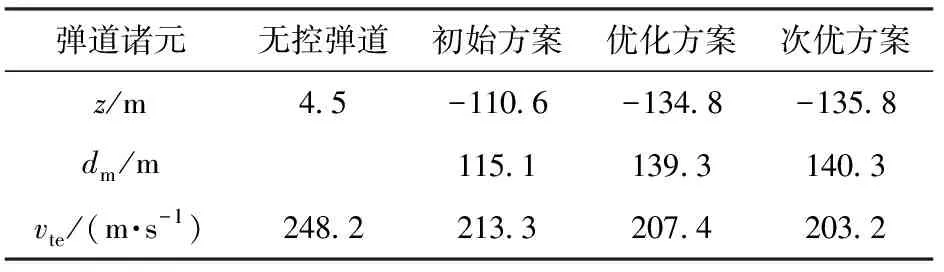
表1 终点弹道诸元

为探究在不同初速下的优化结果，进行不同初速v0和初始射角θ0下的优化设计，取v0=510 m/s、θ0=10°以及v0=170 m/s、θ0=25°进行仿真，并得到相应的终点弹道诸元。表2所示为不同初速条件下的优化结果以及相应的弹道修正量和末速的对比。

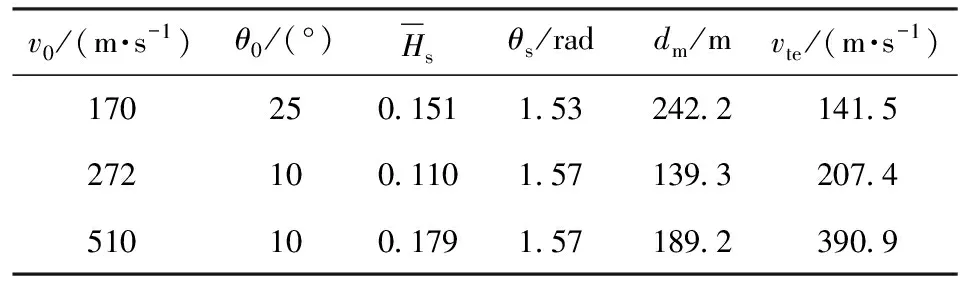
表2 不同初速条件下的扰流片优化结果Tab.2 Optimized results of spoiler at different initialvelocities and elevation angles

由表2可见，不同初速条件下优化的扰流片均具有较大的弧形角且具有合适的高度，在满足扰流片外形尺寸约束的条件下平衡了提升弹丸末速和增大弹道修正能力的需求。

4 结论

本文以某带微型扰流片旋转稳定修正弹为对象，以CFD气动数值计算联立神经网络代理模型，构建了快速获得修正弹扰流片气动力的模式，建立了一个较为实用的扰流片外形多目标优化设计模型。得出主要结论如下：

1)当气流速度为亚跨声速时，同等面积条件下，取较大Hs更有利于增大δM0继而增大修正能力，而取较大θs则对提高升阻比有利。

2)Ma越大，扰流片能够提供的法向加速度越大，而在同等弹目距离下，采用较小Ma飞行有利于提高修正范围。

3)通过对扰流片外形参数的综合优化设计，平衡了弹道修正能力与速度下降的问题，获得了较优的有控弹道性能，研究结果对深入开展该类修正弹的工程研制具有一定参考价值。