钛合金热处理工艺仿真研究进展
朱 磊,肖纳敏,王 浩,沙爱学
(1.中航西安飞机工业集团有限公司,陕西 西安 710089; 2.中国航发北京航空材料研究院航空及发动机材料应用评价中心,北京 100095)
热处理工艺是实现零部件微观组织与性能调控的关键环节。热处理本身是温度、组织转变与应力等交互作用的复杂过程[1-8]。因此在热处理工艺实践中,除微观组织与性能的变外化,由于温度场、结构等因素的影响,热处理过程还会导致残余应力与翘曲变形,对后续的机加和装配过程带来不利影响[6]。由于热处理过程受到多个因素的交互影响,在实践中很难通过物理模拟的方式进行研究,特别是热处理发生在高温阶段,无法对组织、应力、变形等过程进行实时测量,室温状态的分析测试结果很难得到规律性成果。因此采用仿真技术对热处理过程进行虚拟分析,对深入理解热处理过程的组织、应力与温度之间的相互影响规律,指导工艺设计具有重要意义。
钛合金广泛应用于航空、航天等对零件性能和精度要求高的领域,其热处理工艺设计同样面临着组织性能调控、残余应力与变形控制等难题。近二十年来,在钛合金领域,研究者们在热处理相变基础理论、数值模型与软件开发等方面开展了大量研究工作,热处理工艺仿真在固溶时效、退火、热校形等方面得到了深入应用,有助于深入理解钛合金零部件工艺-组织-性能的关联性、残余应力与变形间产生制约机制,对热处理工艺优化设计起到了很好地支撑作用。本文对钛合金热处理工艺仿真基础理论与应用等方面展开综述,并对未来的研究与应用方向提出展望,为钛合金热处理仿真在相关制造领域的应用提供参考。
1 热处理仿真基础理论与模型进展
钛合金的热处理过程包含温度、组织转变与应力三方面交互作用,最关键环节是针对相变和应力的数值模型。因此,目前大部分基础理论与建模的进展主要集中在这两方面。
钛合金在热处理过程中存在多种类型的相变,其中β、α相之间的转变是最基本、最重要的一种,几乎所有钛合金在高温冷却或者时效过程中均会发生。钛合金的β相为体心立方结构,而α相为密排立方结构,两相之间存在严格的Burgers位向关系[9]。当冷却速度较慢时,β-α转变受到溶质元素的扩散控制,两相中的成分会有明显不同。除此以外,当冷却速度很大时,β相转换成α相的过程可能来不及进行,此时β相会发生马氏体相变,转变成与母相成分相同、晶体结构不同的过饱和固溶体,如六方马氏体α′和斜方马氏体α′′,此时相变过程不发生元素扩散,主要发生晶格重构,转变也没有孕育期,相变动力学过程很快。从上面描述还可看出,钛合金基体组织的相变机制与钢铁材料中的奥氏体分解过程比较类似,也存在扩散型和切边型两种类型的相变。同时许多试验研究均表明,β-α的扩散型相变也包含孕育期,相变动力学曲线也类似S型[10]。因此,许多在钢铁材料中的热处理微观组织计算方法也可用于钛合金相变过程的计算。最经典描述扩散型相变的方程是Johnson-Mehl-Avrami-Kolmogorov(JMAK)方程[11-13],也被广泛应用于钛合金的相变动力学模拟。JMAK方程是描述等温过程的相变体积分数与时间的数学关系,通过Schlie叠加原则[14-16],可将非等温相变过程等价为多个微小等温过程的叠加,从而实现任意温度下的微观组织预测,如图1所示[4]。通过对经典JMAK方程的修正与发展,可进一步在模型中考虑初始母相晶粒度的影响[17]。钛合金的β相转变过程中,会形成多种形貌的α相组织。针对钛合金的这种特性,JMAK方程也被进一步发展,可用于预测等轴晶、针状组织等不同形貌α相的体积分数及其动力学特性。Koistinen-Margurger(KM)唯象模型及其变体形式被广泛应用于钢与钛合金的马氏体切变型相变[18-19]。KM模型比较简洁,相变分数与温度之间的关系清晰明了,相关参数很容易确定,在软件二次开发中很容易实现,但是KM模型不能准确描述马氏体相变初始阶段的动力学。

图1 基于JMAK模型、等温相变曲线与叠加原则模拟非等温相变过程
Lusk等根据连续冷却相变理论建立了针对扩散型相变与切变型相变的统一唯象模型[20],这两类相变的体积分数和温度之间的关系可用公式(1)和(2)表示:
(1)
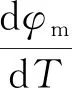
(2)
式中:φd和φm表示扩散相变和切变相变组织的体积分数;φα表示母相体积分数;vd和vm为相变迁移率;α1、α2、β1、β2和ω为相变动力学参数。相关参数通过拟合CCT连续冷却相变曲线获得。
热处理过程中,与微观组织相关的力学响应是另外一个重要的建模环节。由于热处理过程的变形程度较小,为了准确描述其力学响应,其本构模型中必须要包含弹性和塑性,同时还要考虑卸载回弹的影响。为了与微观组织建立关联,目前比较合理的热处理力学本构模型都是建立在单相的基础上,针对每一种相变组织建立力学本构关系,然后整个材料的力学响应通过非线性混合法则来确定[1]。近年来,Bammann、Chiesa和Johnson等从位错理论出发,提出一种基于内变量的力学本构模型,这一模型最初主要用于塑性变形和切削加工等工艺领域。近年来,Bammann-Chiesa-Johnson本构模型也被用于热处理仿真,来描述每一种相的本构关系[21-24]。相比传统的热弹塑性模型,BCJ模型不仅可以准确模拟回弹等因素对变形的影响,还可以实现和应变速率相关的力学响应预测,在较大的温度区间和较大的变形速率范围内,都有很高的模拟精度。根据BCJ模型,每一个相的屈服判据可以用如下公式描述:
(3)
当Dp≥0时,对应相进入屈服状态,否则仍处于弹性状态。在公式(3)中,α为张量内变量,k为标量内变量,σ为偏应力张量,Y为率无关函数,V和f为率相关函数。上述参数可以通过不同温度下的单轴拉伸或压缩应力-应变曲线拟合获得。
在热处理过程中,也必须考虑应力与相变的交互作用,其中一个重要的现象就是相变塑性。相变组织由于晶格参数的不同,往往会发生体积变化。最典型的是在马氏体相变过程中,会发生体积膨胀。这种膨胀会导致新相与母相之间发生相变诱导塑性现象,也就是在外加应力远远低于屈服应力状态时发生的塑性变形。对整个变形影响较大,在实际过程中不可忽略。Greenwood和Johnson建立了一个数学模型来描述这种相变过程中由于蠕变导致的塑性变形,在钢铁材料的热处理仿真中得到了广泛应用。相变塑性效应模型采用如下公式描述[25-26]:
(4)
2 热处理仿真在钛合金中的应用
达索公司的Zhang和Chin等以增材制造工艺为研究对象[28-29],针对钛合金增材制造冷却与热处理过程,构建出相变模拟框架,采用KM方程模拟快速冷却过程的β-α′马氏体相变,JMAK方程模拟钛合金的β-α扩散型相变动力学,模型中考虑了β相的初始晶粒尺寸对相变动力学的影响,也可以进一步模拟α′相的板条束宽度[29]。基于这一框架,在ABAQUS中进行二次开发,成功预测了TC4钛合金在增材制造过程中所得到的微观组织(图2),模拟结果与扫描电镜的试验结果吻合很好。
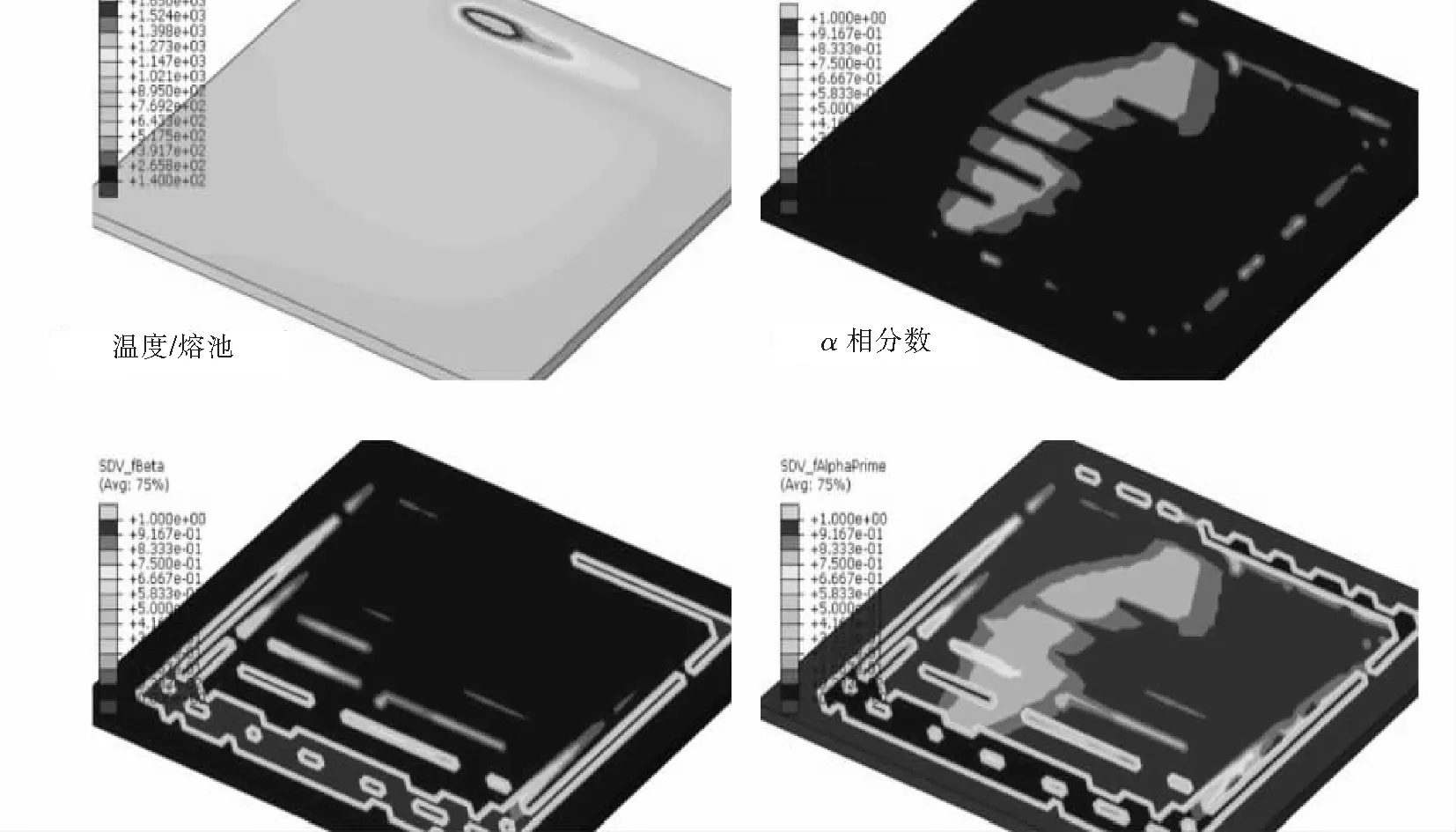
图2 TC4钛合金增材制造热处理过程的微观组织预测
Semiatin等构建出基于平均场理论的相变模型[30],可模拟任意冷却路径下的初生α相晶粒尺寸和体积分数,也可扩展用于TC4和Ti6242合金中的双态组织预测。将此模型和DEFORM有限元软件结合,有限元模拟得到的零件局部位置冷却路径作为输入条件,从而可模拟整个零件截面的微观组织。Regner等采用Johnson-Mehl tessellation和Boolean 模型模拟TC4合金锻造与热处理过程初生α相的形成[31],这一模型同样基于平均场理论,可以与宏观温度场、变形场相互耦合计算求解,如图3与图4所示。Teixeira等提出一个相变模型预测近β钛合金在冷却过程中的相变动力学[32-33]。采用JMAK模型计算晶内魏氏组织的相变动力学,采用形核-长大的平均场扩散理论模拟晶界α相和魏氏组织的动力学与形貌。该模型也可考虑因β相变形所带来的β相晶粒尺寸及亚晶对相变的影响。此模型在Ti17合金和β-Cez合金中应用,成功地预测了不同形态α相的体积分数及其分布。Malinov和Sha等通过DSC试验曲线推导出JMAK方程参数,用于模拟β-α相变后,α晶粒的分数以及形貌[36]。
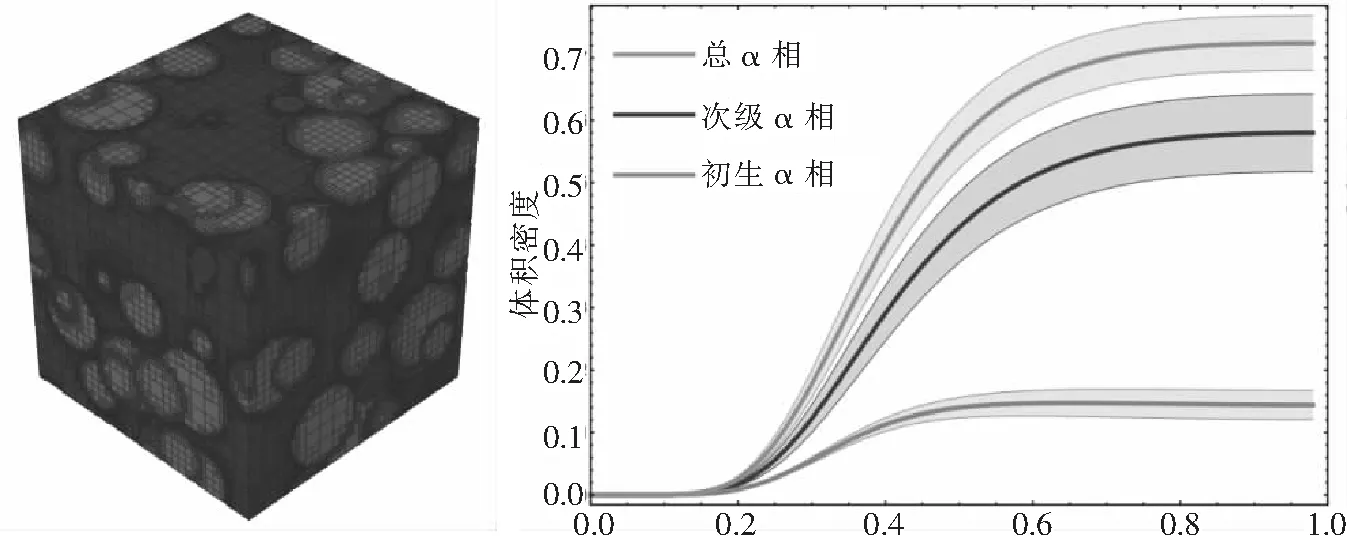
图3 采用3D Boolean模型预测TC4合金热处理过程α相动力学

图4 TC4合金零件热处理后发生的翘曲变形模拟与试验曲线对比(a)及变形实测结果(b)
Schuh等针对在外加应力条件下的钛合金相变超塑性现象提出了一个数学模型,研究表明该模型可准确模拟加热与冷却循环过程中产生的应变增量。结合JMAK方程,就可以建立一个耦合模型,描述温度-应力-相变之间的交互作用[27]。Malinov等建立了神经网络模型来模拟成分与工艺对钛合金微观组织及力学性能的影响[34-35]。由于神经网络模型属于黑箱算法,不涉及任何物理机制与建模,主要通过大量实验数据建立工艺参数、成分与微观组织、力学性能之间的关系。该模型最终决定的是微观组织分数以及对力学性能的影响,无法对应力及翘曲变形进行仿真模拟。Krafft等采用有限元软件Forge构建钛合金热处理过程的相变动力学计算模型。该模型不仅可实现β相和α相分数的预测,还可预测α相的不同形貌及其占比。另外,此模型也常被用于Ti17和Ti-6Al-4V合金航空发动机压气机盘均匀化、锻造、退火的加工全过程[37]。
Odenberger等采用Zener-Wert-Avrami模型描述钛合金的高温应力松弛行为,如图5所示[38]。王伟等基于经典Norton公式建立Ti-6Al-4V合金热粘塑性本构模型[39,43],在对初始残余应力做假设和简化基础上,分析钛合金薄板不同退火温度对退火变形的影响规律,并结合试验验证模拟结果。刘向前等采用有限元法研究TC4薄壁圆筒件热旋压后的冷却温度场分布及冷却后残余应力与变形情况,在此基础上,考虑旋压过程的残余应力,使用蠕变材料模型计算薄壁圆筒件去应力退火的变形情况[41]。由于热旋压温度以及退火温度并未超过β相变点,因此在模拟过程中不用考虑基体相变的作用,主要考虑弹塑性以及蠕变塑性变形。王明伟等研究钛合金真空热处理及热胀形过程数值模拟[42],预测出加热过程的滞后时间,并建立BT20钛合金筒形件真空热胀过程的热力耦合有限元模型,得到可用于工业生产的工艺参数方案。陈涛等建立了TC18钛合金退火态应力松弛行为的本构关系[40],并用于长直杆件焊后退火热处理过程的模拟,研究了退火加热与冷却过程的残余应力与变形规律,结果为变形控制以及后续的热校形工艺提供了指导依据。Alberg等采用数值模拟的方法研究了航空发动机零部件焊接及焊后热处理过程的畸变变形问题[44]。
3 总结与展望
近三十年来,钛合金热处理工艺仿真的基础理论、数值模型与工程应用得到了长足发展,在微观组织分布、残余应力与翘曲变形预测等方面得到广泛应用。目前,在热处理工艺中,引入计算机模拟已成为加工制造业的发展趋势,人们对材料热处理过程采用计算机模拟重要性和意义的认识在不断加深。

(a)高温应力松弛曲线以及模型拟合;(b)钛合金薄板高温热成形后的翘曲变形结果;(c)应力松弛后的翘曲变形模拟结果
钛合金热处理过程的数值模拟虽已取得一定进展,但仍然面临许多挑战。例如,热处理过程涉及到的外部因素复杂,除模型和算法的可靠性外,材料及介质参数的准确性也是非常关键的环节。这些参数包括热物性参数(导热系数、热容、热膨胀系数、相变潜热)、力学性能参数(弹性模量、泊松比、屈服强度、塑性模量)、相变动力学参数、相变膨胀系数、相变塑性系数和淬火过程中的工件表面各处的换热系数等[3]。以界面换热系数为例,这一参数是决定工件温度场分布的核心参数,与介质、工件以及实际的工艺实施方案密切相关。因此在实际热处理仿真中,必须要结合现场实际条件进行测量和反求,才能让模拟结果接近实际情况。此外,热处理残余应力和变形的高精度仿真仍然是一个难点,一方面残余应力很难通过试验进行准确验证和校核,需要发展先进的残余应力试验技术对相关模型和算法进行验证;另一方面热处理变形涉及到的温度范围宽,影响因素较多,对材料的本构模型与计算精度提出很高要求,需要进一步进行深入研究[1]。
近年来,基于介观尺度的微观组织演化计算方法也得到了很大的发展。以相场方法为代表的介观计算方法可从机理上模拟钛合金热处理过程发生的相变[45-49],不再局限于JMAK模型等平均场理论,可从单个晶粒的层次来模拟微观组织演化,不仅可预测相变组织及其体积分数,还可预测组织形貌、溶质元素分布甚至新相变体取向规律。未来随着计算机能力的增强以及算法的发展,有望将介观尺度微观组织演化计算方法与宏观的温度场以及应力/应变场进行耦合计算,从而使热处理工艺仿真向多尺度方向发展,使材料设计与零部件制备有效结合起来。未来随着基础理论、模型和材料数据库的不断完善,热处理技术终将摆脱凭经验依赖,向精确预测、定量控制和设计制造一体化与智能化的方向飞跃。

