速率常数在浮选过程中的变化机制研究进展

霍怡屹，祖 伟，姜 帆，马嘉成，赵慧洁，李金雨，常 甜，马力强，李吉辉

(1.中国矿业大学(北京) 化学与环境工程学院，北京 100083；2.宜章弘源化工有限责任公司，湖南 郴州 423000)

浮选是细粒矿物分选最为常见的方法之一，其过程涉及气、液、固三相的复杂物理化学变化，受到诸多因素影响[1]。浮选动力学研究是通过建立浮选动力学数学模型，引入浮选速率常数、最大可燃体回收率等参数来验证或评价浮选效率。其中，浮选速率常数K作为浮选动力学模型中的主要参数，随时间的变化规律及同一种矿物中不同K值的分布规律是浮选动力学模型研究的热点内容[2]。浮选动力学研究的不断深入，对揭示浮选过程的实质、控制或模拟浮选设备、优化浮选工艺等实际问题具有重大的意义。

本文详细描述了国内外学者对K值的研究进展，K值的深入研究促使浮选动力学模型得到不断发展。不同矿物的性质、不同浮选药剂的性能、不同浮选设备的性能以及不同的操作条件，都会影响到K值的大小。随着浮选过程的进行，槽内目的矿物K值是如何随时间变化的，某一种矿物中K值是如何随空间分布的也是学者们深入研究的重点[3]。K值随时间的变化规律与在空间中的分布规律也存在着一定的因果性、关联性。有学者[4]通过经验性、分析性推导，证明了二者之间存在的本质联系。在前人的理论基础上针对某种动力学行为、特定矿物或影响因素，提出变量与浮选速率常数K的实用特定性关系式，建立新的浮选动力学模型，增加了模型的适用性和精度，促进了模型的进一步发展。目前浮选动力学模型的主要应用有解释评价浮选工艺和药剂以及优化浮选设备的结构设计等[5]，浮选速率常数K在模型应用中起着至关重要的作用。在实际应用中，将不同药剂种类或用量、不同工艺等操作条件下的浮选实验数据与常见的浮选动力学模型进行拟合，通过对比浮选速率常数K值的大小及变化，寻求最优实验条件，为提高浮选效率提供理论支持。

然而，目前浮选动力学的研究还不够深入，浮选速率常数-颗粒与气泡的接触时间、诱导时间、颗粒与油滴的碰撞概率、粘附概率等微观变量之间的关系还有待进一步探索。由于拟合算法或模型假设的原因[6]，使得模型中极限回收率的求解出现偏小或超过100%的不合理、不准确的情况。因此优化算法，精确求解K值，更准确地描述浮选过程，是未来浮选动力学研究的一个方向。

1 浮选速率常数的变化机制

1.1 浮选的动力学理论基础

20世纪30年代，赞尼格[7]将化学过程中的动力学应用到浮选过程，作为建立浮选动力学模型的基础，建立了一级动力学模型，又称浮选速率常数方程[7]。其微分基本形式为：

式中，c为t时刻浮选槽内待浮矿物的浓度，k为浮选速率常数。

该方程式的物理意义是浮选速率正比于槽内该矿物的浓度[8]。但经实验证明，大部分浮选过程不符合一级浮选速率过程。于是有学者[7]提出n级浮选动力学模型，其基本形式为：

式中，n为反应级数，其范围为0～6。

上述浮选动力学模型认为浮选速率常数为恒定常数，且阶数的求解只能利用作图法得出。由于这些模型仅仅考虑了速度与浓度之间的关系，忽略了各个系统间复杂的物理化学影响，因此不能完全表达出浮选的全部过程，只能作为经验模型进行实验验证。

20世纪60年代后，国内外学者[9]进行了大量研究，认识到浮选过程与一般化学反应过程存在差异。浮选物料的性质、浮选设备的相关特征、浮选物料在浮选槽内空间的不均分布以及捕收剂吸附的不均匀性等因素都影响着浮选过程。因此，不同矿粒有不同的浮选行为，同一种物料的浮选速率常数K不是一成不变的。故浮选动力学模型中浮选速率常数K值如何随空间和时间分布，逐渐成为浮选动力学研究的热点问题[11]。随后对浮选动力学模型进行优化主要围绕K值随时间变化的规律以及同一矿物中K值的分布规律两方面进行[4]。

1.2 浮选速率常数的时间函数

1957年，哥利科夫[11]提出目的矿物的浮选速率常数K应随着浮选时间的变化而变化。他提出的修正方程为：

式中，ε为目的矿物的回收率；a和b为根据试验求出的常数；t为浮选时间。式(3)的积分式为：

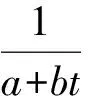
不同于哥利科夫经验性的推导方法，1978年陈子鸣[11]在探索K值与时间的关系时，划分试验的时间区域，逐段求算某一时间间隔内的平均K值。当把时间取得足够短时，使得K值随时间的变化形成一个连续函数，即为：

在研究连续函数K(t)的形式时，根据K值越高，浮选速率越大，单位时间内浮出物的量越大，则槽内平均K值的变化越大的准则提出了瞬时K值变化量正比于槽内平均K值的关系积分式，即为：

解得：

K(t)=Kme-t

(7)

将式(7)带入式(5)推导出包含时间因素在内的浮选速率常数模型，即陈子鸣模型，具体形式如下：

εt=ε∞{1-e-[KL(1-e-C(t-1))+K1]}

(8)

式中，KL为K(t)的最大值减去K1，C为常数。

在陈子鸣模型的基础上，刘逸超[12]用解微分方程的方法，运用不同的物理逻辑推导出了与陈子鸣模型略有不同的刘逸超模型。刘逸超[12]认为矿浆内有用矿物群的平均K值的变化与矿浆内有用矿物群的平均K值成正比关系，即式(7)，与陈子鸣的想法相同，但是刘逸超直接将方程(9)与方程(1)联立，解得刘逸超模型为：

1.3 浮选速率常数的分布函数

在实际矿石浮选时，同种矿物中存在有组成不同、解离度不同以及表面性质不同的颗粒，故引出“品级”的概念。可浮性相同并具有相同一级反应速率常数的这些矿粒称为一个品级。因此在实际浮选中，由于浮选物料由不同K值的品级组成，具有较大浮选速率常数的物料以较快速率浮出，而速率常数低的以较慢速率浮出。各个品级的物料具有不同的K值，故各品级的数量比例发生变化，则用分布密度函数来表示。

1963年今泉常正[13]和井上外志雄首次提出同种矿物具有不同的K值，并用K值的分布来解释浮选过程的ε-t关系是非线性的原因，即K值随时间变化是由于K值较大的颗粒先离开槽体，而K值小的还留在槽体当中，这就导致了从总体上看K值随时间延长而减小。

1965年E.T伍德本利和B.K罗弗第研究了K值的概率密度分布函数。提出了平均K值与分布函数间的关系并认为K值的分布服从双峰Γ函数分布，即：

f(K)=CKae-bK

(10)

式中，f(K)表示任意K值在总量中的分布；C为常数，C=ba+1/Γ(a+1)，其中Γ(a+1)=a!，a，b为常数。

陈子鸣[3，11]在探讨K值的分布问题时，利用逐步积分法，复原K值密度分布函数，认为K值在原矿中的分布函数近似于β分布；许长连[14]在研究浮选速率常数K值时认为不能充分表达工业矿石浮选过程中各待浮矿粒本身的可浮特性，所以由绝对浮选速率常数K值转化为相对于气泡的相对浮选速率常数K值，并推导复原的连续型K值分布函数的概率密度函数，符合Γ分布。

1986年尹蒂[4]将浮选过程从K值随时间变化和随空间分布两方面进行了探讨和计算，推导出了通用的速率常数分布模型基本公式，介绍了K值和K值分布的关系。K值随时间变化下降速率与t时刻槽内待浮物料的K值分布的方差成正比，方差越大，平均K值下降越快，方差越小则下降越慢。在浮选实验初期，欲浮物料的可浮性分布广，差异大，浮选速率较高、可浮性好的物料先浮出；随着浮选实验的进行，槽内剩余物料的浮选速率越来越小，它们之间的差异也越来越小。故方差σ2(t)和K(t)都随时间而减小。

1.4 特定性浮选动力学模型的建立

在浮选动力学模型的应用中，得到广泛应用的通用型模型主要有以下几种[15]：

经典一级模型：

ε=ε∞(1-e-kt)

(11)

一级矩形分布模型：

二级动力学模型：

二级矩阵分布模型：

为更有效地指导实践工作，进一步优化动力学模型，不少研究者围绕K值的时间规律和分布规律，在通用型模型的基础上推导出适用于特定条件下的浮选速率模型。研究并建立特定型新型浮选动力学模型能有效提高模型的精度及适用性。

有学者研究了窄粒级煤泥浮选的动力学模型。陶有俊等[16，17]发现一级动力学模型对窄级别煤泥浮选速率方程的拟合度最高，导出了煤泥浮选速率常数K与捕收剂用量及起泡剂用量之间的方程：

K=a0+a1d+a2c+a3f+b1d2+b2c2+b3f2+e1cf

(15)

式中，d为煤泥密度；c为捕收剂用量；f为起泡剂用量；a、b和e均为模型参数。在此基础上，又对大量试验数据进行拟合，求得常数a、b、e的值代入上式，得出特定的浮选速率常数模型。

王黎伟[19]以磷矿为研究对象，进行了充填式浮选柱的动力学研究。采用非线性最优化的估计方法，对五种常规浮选动力学模型进行拟合，并分析误差，得到一级浮选动力学最为合适。并将气含率与浮选动力学常数K进行关联，得到浮选速率常数K与气含率的数学表达式：

K=18εgsin2{2arctane-1.76+0.26×exp[-92103×(εg-0.063)2]}

(16)

式中，εg为气含率。该表达式的提出提高了柱式浮选动力学模型对浮选柱分选行为评价的准确性。

李俊旺[18]以会泽铅锌矿中的方铅矿、闪锌矿和黄铁矿为研究对象，系统研究其可浮性及浮选速率特性，运用积分复原法对铅锌硫化矿浮选过程的浮选速率常数K的分布进行了分析。并以一级浮选动力学模型为基础，建立了针对该矿样的分速浮选模型，即分布式动力学模型中的成分按浮选性能分为快和慢两种，具体表达式如下：

ε=εmax-[εfmaxe(-kf×t)+(εmax-εfmax)e(-ks×t)]

(17)

式中，ε为浮选回收率；εmax为最大回收率；εfmax为快浮最大回收率；kf为快浮浮选速率常数；ks为慢浮浮选速率常数。将上式与一级、二级动力学模型的拟合数据进行对比，发现新提出的分速模型拟合度更高，能更好地模拟浮选过程。

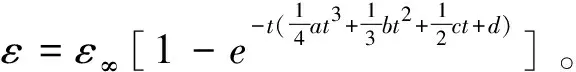
以上特定性浮选动力学模型建立的方法有两种。一是基于浮选速率常数的时间规律，运用时间微元化的思路得到速率常数K与时间t的表达式，带入到通用浮选动力学方程中，使经典的动力学模型更为精确；二是基于浮选速率常数的分布规律，探索各类矿物性质与操作变量等影响因素与K的关系，丰富了浮选动力学模型的内涵，使特定性模型在该条件下与实际浮选过程的拟合度更高。

2 浮选速率常数对实际工作的指导作用

浮选速率常数作为浮选动力学模型中的重要参数，在指导实际浮选过程中代表了浮选的快慢及效率。通过实验数据与浮选动力学模型的拟合，观察K值的大小和变化可以评价或解释动力学行为或工艺、药剂种类及用量以及浮选设备的结构参数。

1999年，有学者[21]引入了修正浮选速率常数和选择性指数的概念。在实验室研究中，一个变量导致极限回收率R∞与K值的同时变化，使得难以确定不同条件下的K值的变化趋势。改进的浮选速率常数定义为R∞与K值的乘积，选择性指数则定义为两种矿物的修正浮选速率常数之比。用修正浮选速率常数和选择性指数两个参数代替传统的速率常数，可以更加精确地解释和评价浮选效率的高低。修正后的浮选参数更多地应用于描述两种相似矿物分离的浮选过程。

侯波等[22]探究了捕收剂AY对石英浮选的上浮率和浮选速率常数的影响。实验探究了pH=4.0，不同AY浓度下，各粒级石英的上浮率与时间的关系。将实验数据与六种浮选动力学模型进行拟合，发现随着捕收剂浓度的增加，浮选速率常数K值增大，直至最佳捕收剂浓度之后，增幅明显变缓。因此，得到最大浮选速率K的捕收剂浓度就是石英浮选的最佳AY捕收剂浓度。

Kunkun Zhen等[23]人采用等离子氧化法研究了氧化柴油对低阶煤浮选动力学的影响。以神东矿区的长焰煤为煤样，分别研究了柴油氧化前后含氧官能团、反应热、润湿性等性质，并将浮选速率实验的数据与五种浮选动力学模型进行拟合，将拟合得出的浮选速率常数K及最大可燃体回收率进行对比，得出结论：对于低阶煤浮选，在给捕收剂用量的情况下，氧化后柴油的动力学模型中的浮选速率常数K和最大可燃体回收率数值均比原柴油模型中的数值更高，从理论层面验证了氧化后柴油相较于普通柴油具有更好的起泡性能。

方夕辉等[24]采用快速浮选方法，考察了矿浆浓度、矿物粒度以及浮选机转速三种因素对黄铜矿、黄铁矿的浮选动力学行为的影响，研究了黄铜矿、黄铁矿人工混合矿快速浮选动力学，并证明了依据两种矿物浮选速率的差异，快速浮选分离混合矿的可能性。试验结果表明，对于单一矿物，K值在一定范围内随矿浆浓度的增加、矿物粒度的减小以及浮选机转速的增加而增加。而对于混合矿，粗粒黄铜矿K值要大于细粒K值。因此在两者K值差异最大的操作条件下即可实现粗粒铜矿粒的快速浮选。

孙浩然[25]为了得到最优调整剂种类及药剂用量，研究了不同浓度的调整剂(碳酸钠、氯化钙和氯化镁)对菱镁矿及其伴生矿物白云石浮选回收率及浮选速率的影响。实验结果表明，两种矿物的速率常数K随浮选时间的延长总体呈降低趋势，该规律符合实际浮选过程中K随时间延长的变化。在碳酸钠和氯化钙做调整剂时，白云石的浮选速率K值大于菱镁矿；但在氯化镁做调整剂时，菱镁矿的K值大于白云石。同时，氯化镁浓度为2.0mmol/L时，菱镁矿与白云石的浮选特性差异较为显著，回收率和K值差异大，故选用2.0mmol/L的氯化镁做调整剂。

刘宜萍等[26]探究了不同pH、添加不同金属离子条件下，煤泥浮选速率及浮选回收率的变化。选用三种浮选动力学模型与实验数据进行拟合，选取拟合度最高的模型中的浮选速率常数K表征不同条件下的浮选速率。结果表明，在全部pH条件下矿物质的浮选速率常数K始终低于煤的浮选速率常数K，理论上解释了煤粒先于矿物质上浮的实验现象。在常规浮选动力学实验的基础上，分别添加NaCl、CaCl2、FeCl3至润湿矿浆中，结果表明添加金属阳离子使浮选过程的速率增大即K值增大，故金属阳离子对煤和矿物质浮选速率具有促进作用。

繆亚兵等[27]研究了在油酸和水玻璃体系中，萤石粒度、浮选药剂用量、浮选矿浆质量浓度、浮选机叶轮线速率等因素对萤石浮选回收率ε和浮选速率常数K值的影响。结果表明，浮选速率常数K随油酸用量的增加而增大后趋于平缓，而随着水玻璃的用量增加略有降低，为保证浮选效率确定了油酸和水玻璃的比例及最佳用量；浮选速率常数K值也随浮选矿浆质量浓度增大先增大，后减小；随着萤石粒度的减小，K值逐渐升高，但回收率略有降低；回收率和K值也随叶轮转速的增加而增大，为日后提高浮选速率提供了理论依据。

Omid SALMANI NURI等[28]研究表面酸溶解对钛铁矿及其常见伴生脉石矿物透闪石-斜绿泥石浮选动力学的影响。经表面溶解后，从Ol-Px、Tr-Cch和石英中浮选钛铁矿的修正速率常数值分别从36.15min-1、36.52min-1和47.86min-1增大到41.72min-1、45.78min-1和56.24min-1，导致从脉石矿物中分离预处理过的钛铁矿过程的动力学选择性指数(SI)增大，表明表面酸溶解能很好地促进钛铁矿的浮选。

金会心等[29]通过经典的一级浮选动力学模型推导出反浮选的动力学模型，建立了稀土磷矿物和脉石矿物的回收率随时间变化的模型。通过浮选正交数据分别探讨了捕收剂WF-01和抑制剂H3PO4与修正速率常数的关系、捕收剂WF-01和抑制剂H3PO4与选择性指数的关系，并建立了二元二次回归方程找到最优的捕收剂和抑制剂的用量。

Asghar Azizi[30]研究了铜矿浮选中修正浮选速率和选择性指数的相关问题。通过对门萨尔梅铜矿进行分批浮选实验，将实验数据与经典一级浮选速率方程和一级矩阵方程拟合得出修正后的浮选参数。随后又考察了浮选矿浆酸碱度、矿浆固含量、捕收剂用量和捕收剂类型等操作参数对修正后动力学参数的影响。最终根据拟合结果确定了一系列最佳的操作参数，当Kmod最大且铜矿与铁矿间的SI值最大时，在该条件下，浮选效果最好。

M.Ucurum等[31]研究了捕收剂类型、粒度分布、捕收剂用量、气流流量、矿浆密度等参数对浮选参数在浮选柱中闪锌矿浮选中的影响。将浮选实验数据使用SPSS统计程序以“非线性回归”模式进行处理。结果表明，二硫代戊酸钾对锌的修正速率常数(0.252)相较于戊基黄原酸钾(0.192)较高，同时粒度、浮选柱气流流量、矿浆密度等操作参数的最佳条件也由修正浮选速率和选择性指数共同决定。

3 结语与展望

浮选速率常数的深入研究不仅推动浮选动力学模型的不断发展，也使浮选动力学在实际工作中的应用更加广泛。本文针对浮选速率常数变化机制的研究和对实践的指导进行了综述，主要结论如下：

1)随着浮选速率常数K的理论研究不断深入，探索出了其随时间变化的规律和随品级变化的分布规律，并以这两种规律为理论基础，不断探索新型的浮选动力学模型，建立特定适用性模型，提高模型的实用性及精度，推动浮选动力学模型的发展。

2)本文论述了以深入研究浮选速率常数K为基础的浮选动力学在实际工作中的应用。探讨了矿物性质、浮选药剂的性能、浮选设备的性能和操作因素等方面对浮选速率的影响。通过比较不同的操作条件下的K值的大小与变化，评价解释实验现象，指导实际工作。修正浮选速率常数和选择性指数替代传统浮选速率常数来指导实际工作更具有精确性。

探索微观变量与浮选动力学常数的关系，优化拟合算法，精确求解浮选速率常数，进而建立更加完整的、精确的浮选动力学模型是今后研究的重点和热点问题。