基于改进Canopy-K-means算法的并行化研究
王 林,贾钧琛
(西安理工大学 自动化与信息工程学院,西安 710048)
0 引言
随着互联网普及率的不断提高,网络数据呈几何级增长,面对海量以及快速增长的网络数据,通过聚类分析可以快速准确地从中挖掘出价值信息。但是,传统的聚类算法无论是在聚类精度,还是在执行时间上都已经不能很好地满足当前需求,利用分布式计算框架对其进行并行化改进,不仅可以缩短聚类时间,还可以增强算法的扩展性,更好地满足当下数据挖掘的需要。
K-means算法作为一种具有代表性的聚类算法,具备较快的收敛速度、可靠的理论以及容易实现等诸多优势,因而被人们广泛应用于各行各业,但是算法也存在聚类中心点的选取具有随机性,需要提前确定聚类个数等不足[1]。对此,许多学者对K-means算法进行了改进并取得了一定的成果。
邓海等人[2]结合密度法和“最大最小原则”优化K-means初始聚类中心点的选择,算法准确率得到提高,但是改进后算法的时间复杂度较高,运行时间较长。赵庆等人[3]通过Canopy算法对数据集进行“粗”聚类,避免了传统K-means中心点选取存在的盲目性,极大提升了其准确性,然而在采用Canopy算法初始阈值需要人为指定,所以聚类结果不稳定。刘纪伟等人[4]结合密度思想优化了K-means初始中心点的选取,同时引入聚类有效性判别函数确定值,提高了算法的准确度,但是也增加了算法的运行时间,执行效率较低。李晓瑜等人[5]结合MapReduce分布式框架并行化实现改进的Canopy-K-means算法,并行化实现的算法具有良好的准确率和扩展性,但是Canopy算法初始阈值人为指定的问题仍然存在。
上述工作均是针对K-means算法初始中心点随机选取的不足进行改进,一定程度上提高了算法的聚类准确度,然而仍旧存在不足。本文首先针对Canopy-K-means算法中Canopy中心点随机选取的不足,引入“最大最小原则”进行优化,此外,定义深度指标计算公式,确定Canopy中心点的最优个数及区域半径;接着借助三角不等式定理对K-means算法进行优化,减少冗余的距离计算,加快收敛速度;最后结合MapReduce分布式框架将改进后的算法并行化实现。在构建的微博文本数据集上进行实验,结果表明改进算法的准确率和扩展性都得到提升。
1 MapReduce并行框架
MapReduce[6]是一种用于处理大规模数据的分布式编程模型,可以将大型任务进行拆分处理,从而加快数据的处理效率。
MapReduce主要包括Map和Reduce两个函数,在数据处理过程中,数据均以键/值对形式保存。其中,Map函数根据用户输入的键/值对生成中间结果,而Reduce函数对中间结果进行归并处理,得到的最终结果同样以键/值对形式输出。除了Map和Reduce两个核心函数外,还提供了Combine函数,它在Map后调用,相当于本地的Reduce,主要是为了减少从Map到Reduce的数据量。
2 Canpoy-K-means聚类算法研究与改进
2.1 Canpoy-K-means算法研究
K-means算法由于算法简单、易于实现等优点而被广泛使用。其基本思想是:从数据集中随机选取K个数据对象作为初始聚类中心点;将剩余数据对象和簇中心进行间距计算,并且把它划至间距最短的簇中,持续该过程,直到数据集为空集;然后根据簇中的数据对象计算新的聚类中心点,继续上述过程,直到簇的中心点不再发生变化或者符合停止条件,迭代才会停止,完成聚类划分。
Canpoy-K-means算法是一种借助Canpoy算法改进的K-means算法。在Canpoy-K-means算法中,通过Canpoy算法对数据集进行“粗”聚类,得到个Canpoy子集,随后再以个Canopy子集的中心点作为K-means算法的初始中心点进行“细”聚类,生成聚类结果。Canpoy-K-means算法执行步骤如下:
1)将待聚类数据集构成List集合,然后指定两个距离阈值T1和T2(T1>T2);
2)随机选取List合中的一个数据对象P,构成一个新的Canpoy,并将对象P从集合List中移除;
3)对于List中剩余的数据对象,计算与对象P之间的距离。如果间距小于T1,就把它分配到对象P所在的Canpoy中;如果与对象P的间距小于T2,则将它从List中删除;
4)重复步骤2)和3),直到List为空;
5)将形成的Canpoy子集数目作为K值,Canpoy子集的中心点作为初始的聚类中心点进行K-means聚类,得到较为准确的聚类结果。
Canpoy-K-means算法虽然解决了K-means算法人为指定值和初始中心点随机选取的不足,然而其也存在不足:Canopy的初始聚类中心点随机选取和初始阈值人为指定,具有盲目性,初始阈值对聚类所得的最终结果具有显著影响,一定程度上降低了聚类结果的稳定性;另外,由于其具备较高的时间复杂度,串行执行过程时所需时间较长,算法串行执行效率较低。
2.2 Canpoy算法改进
为了改善Canopy算法初始阈值人为指定以及初始中心点随机选取的不足,本文引入“最大最小原则”对其进行优化,提高算法的准确率以及聚类结果的稳定性。
基于“最大最小原则”的中心点选取方法基本思想如下:在将数据集划分为若干个Canopy的过程中,任意两个Canopy中心点之间的距离应尽可能远,即假设目前已生成个Canopy中心点,则处于第n+1位的Canopy中心点应为其它数据点和前n个中心点间最短间距的最大者[7],其公式如下:
(1)
式中,dn表示第n个中心点与候选数据点的最小距离;DistList表示前n个中心点与候选数据点最小距离的集合;DistMin(n+1)则表示集合DistList中最小距离的最大者,即Canopy集合n+1的第个中心点。
基于“最大最小原则”的Canopy中心点选择方法,在实际应用中符合下述情况:如果中心点数量和最佳中心点的数量较为接近,此时DistMin(n+1)具备最大的变化幅度。所以,为了确定最优的Canopy中心点个数及区域半径Depth(i),根据参考文献[8]提出的边界思想,采用深度指标T1,描述Canopy中心点的变化幅度,如公式(2)所示:
Depth(i)=|DistMin(i)-DistMin(i-1)|+
|DistMin(i+1)-DistMin(i)|
(2)
当i接近真实聚类簇数时,Depth(i)取得最大值,此时设置T1=DistMin(i)使得聚类结果最优。
2.3 K-means算法改进
传统K-means算法需要迭代计算数据对象与中心点的间距,完成数据对象的划分,然而在该过程中存在许多不必要的距离计算,为了减少K-means算法的计算量,加快算法的收敛速度,本文引入三角不等式定理对其进行优化改进[9]。
定理1:任意一个三角形,两边之和大于第三边,两边之差小于第三边。由于欧式距离也满足三角不等式的特性,因此将其扩展到多维的欧几里得空间可知:对于欧式空间的任意向量x、b、c,满足:d(x,b)+d(b,c)≥d(x,c)和d(x,b)-d(b,c)≤d(x,c) 成立。
对于任意一个向量x和两个聚类中心b、c,根据三角不等式定理可得:d(x,b)+d(b,c)≥d(x,c),但是为了避免计算距离d(x,b),需要得到d(x,b)≤d(x,c)这个不等式关系,给出引理及其证明过程如下:
引理1:假设xp是数据集中的任意一个向量,ci是向量xp当前的簇中心,d(xp,ci)已知且cj是除ci外的任意一个簇中心,如果2d(xp,ci)≤d(ci,cj),则有d(xp,ci)≤d(xp,cj)。
证明:假设有2d(xp,ci)≤d(ci,cj),两边同时减去,得d(xp,ci)≤d(ci,cj)-d(xp,ci),由定理1可得d(ci,cj)-d(xp,ci)≤d(xp,cj):因此可以得到结论d(xp,ci)≤d(xp,cj),即向量xp属于簇中心ci。
根据引理的推导过程可知,基于三角不等式的改进方法可以有效减少K-means冗余的距离计算,应用如下:已知是数据集中任意一个向量,ci是向量的当前簇中心,d(xp,ci)已知且cj是另外的任一簇中心,根据引理1可知,如果2d(xp,cj)≤d(ci,cj),则可以确定数据向量xp属于簇中心ci,此时就不再需要计算d(xp,cj)。
2.4 改进算法的MapReduce并行化实现
本文主要从两方面对Canopy-K-means算法进行改进,首先引入“最大最小原则”优化Canopy中心点的选取;接着利用三角不等式对K-means算法进行优化,减少冗余的距离计算,加快算法的收敛速度。改进后的算法主要分为两个阶段,其流程如图1所示。
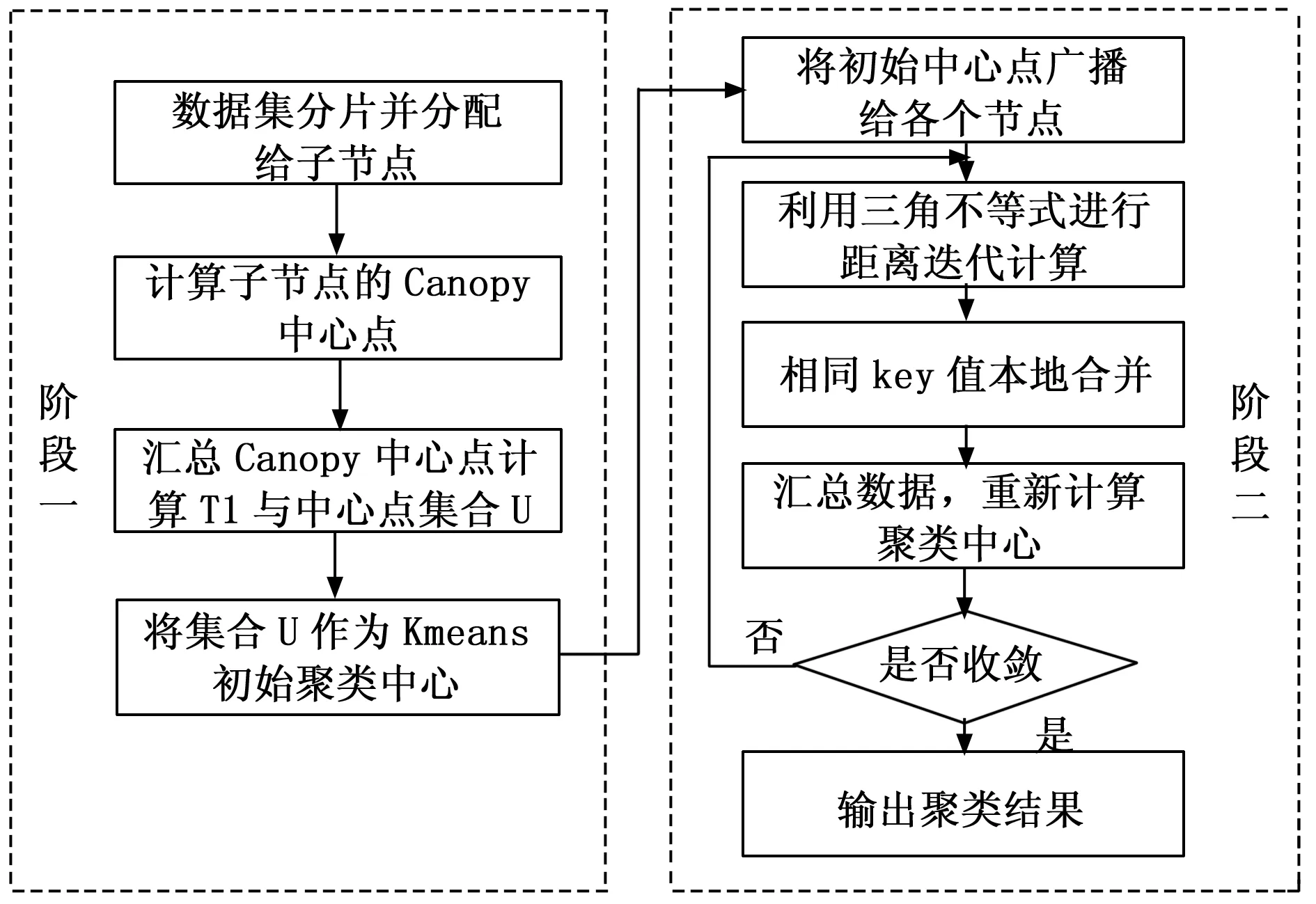
图1 改进Canopy-K-means算法流程图
阶段一:基于“最大最小原则”改进的Canopy算法在MapReduce框架上的并行化实现,用来选取初始聚类中心点及K值。该阶段由Map函数和Reduce函数两部分完成。算法的伪代码如下:
Map函数
输入:节点数据集合List
输出:节点Canopy中心点集合Ci
1)Ci=null
2)While (List!=null)
3)If (Ci=null)
4)在List中随机选取一个数据点作为Canopy中心点,保存至Ci中,并将该数据点从中删除
5)Else if (Ci!=null)
6)遍历计算中的数据点到集合Ci各个中心点的距离,取距离的最小值dn保存到集合中
7)求出集合D中的最大值Max(D)
8)把Max(D)对应的数据点作为Canopy集合的下一个中心点,存入集合Ci中
9)End If
10)End While
11)output(Ci)
Reduce函数:
输入:各个节点在Map阶段产生的局部中心点集合C{C1,C2,C3,…,Cn}
输出:Canopy中心点集合U;
1)计算集合C中的数据总量K=Count(C)且令j=0
2)while(j 3)计算全局Canopy中心点集合C中Depth(i)的最大值 4)令T1=Max(Depth(i)),j++ 5)把集合C中的前i个中心点赋值给集合U 6)End While 7)K=Count(U) 8)OutPut(U) 阶段二:将阶段一得到的Canopy中心点作为初始中心点完成K-means聚类。此外,在此阶段引入三角不等式定理,减少迭代过程中不必要的距离计算。该阶段由Map函数、Combine函数和Reduce函数三部分组成。算法的伪代码如下: Map函数 输入:K值和Canopy中心点集合U,数据集X={x1,x2,x3,…,xn} 输出:聚类中心点集合W 1)While (W!=U) 2)计算集合U任意两中心点间的距离d(c,c′) 3)保存最短距离S(c)=min(d(c,c′)) 4)计算数据集X中的数据点到集合U中第i个中心点的距离dist[i] 5)If (2dist[i]≤S(c)),则标记该数据点属于第i个Canopy中心点的簇,然后从X中删除该数据点;对于不符合条件的数据点,保存其到该中心点的距离 6)If (X!=null) 7)计算不符合条件的数据点与中心点的距离,将其划分给距离最小的簇中心并进行标记 8)计算被标记点的新簇中新W′ 9)If (W=W′) 10)Break 11)Else 返回2)重新计算 12)End While Combine函数: 输入:X中数据点所属簇下标key,key值所属的键值对列表 输出:X中数据点所属簇下标key,各个簇内被标记数据点的各维累加值以及值key所属的键值对列表; 在本地解析各维坐标值,求出各维的累加值,并保存到对应列表中。 Reduce函数: 输入:X中数据点所对应下标key,key值所属的键值对列表 输出:X中数据点所属簇的下标key,最终的簇心W 1)初始化Num=0,记录所属簇内数据点的个数 2)While (X.hasNext()) 3)解析X.next()中的各维下标值,计算样本个数num 4)计算各维下标值的累加和并进行存储 5)Num+num 6)End While 7)用各维下标的累加和除以Num,计算新的簇中心W Reduce函数结束后,对比新生成的簇心和之前的簇心是否相同,若簇中心相同,则算法结束,否则继续执行上述过程,直到簇中心不再变化。 本文的Hadoop集群环境搭建在一台I7CPU,16 G内存,2 TB硬盘服务器之上。集群包括1个Master节点和5个Slave节点,每个节点均为2 GB内存,200 G硬盘,操作系统为CentOs 6.5,jdk为jdk1.8.0_181,Hadoop版本为2.7.3,程序开发工具为Eclipse,算法全部由Java语言完成。 实验的数据集是经过中文分词、去停去重和文本特征提取等预处理后的微博数据。本文共构造了100 M、500 M、1 G和2 G这4个数据量依次递增的微博数据集,用于改进Canopy-K-means算法的测试。 3.2.1 算法准确率分析 本文以准确率(precision)、召回率(recall)和F值作为评判指标[10]。对比传统K-means算法(算法1),Canopy-K-means算法(算法2)以及本文改进算法(算法3)在文本聚类上的优劣,分别在100 M、500 M、1 G和2 G数据集各聚类10次,取各项指标的平均值进行比较,结果如表1所示。 表1 文本聚类测试结果 由表1中的测试结果可知,与常规K-means算法相比,Canopy-K-means算法的准确率提升了约10%,而本文改进算法与Canopy-K-means算法相比,准确率提升了约7%。这是由于改进后的Canopy-K-means算法,优化了Canopy的中心点的选取,根据深度指标计算公式,确定了Canopy中心点的最优个数与最佳区域半径,从而使得聚类结果更加稳定,算法的准确率得到提高。 3.2.2 算法扩展性分析 加速比是常用来衡量程序并行化执行效率的重要指标。它的定义如下:Sp=Ts/Tp。此处,为在单机条件之下算法运行的具体时长,而Tp则是在并行条件之下算法运行的具体时长。加速比Sp越大,表示算法的效率越高。考虑到单机环境处理大规模数据时系统容易崩溃,因此本文以1个数据节点下算法的执行时长作为。 为了对比改进后算法和未改进算法在扩展性上的差异。使用K-means算法、Canopy-K-means算法以及改进的Canopy-K-means算法分别对1 G的数据集进行5次聚类运算,取其平均运算时长,计算其加速比,测试结果如图2所示。 图2 相同数据集不同算法加速比 根据图2可知,在相同规模节点数目下,本文改进算法的执行效率明显优于其它两种算法,这是由于“最大最小原则”的中心点选取方法优化了Canopy中心点的选取,减少了算法的迭代次数,并且基于三角不等式定理改进的K-means算法,有效减少了迭代过程中存在的冗余距离计算,算法的执行速度得到提高。 为了验证改进后算法在不同数据集上的并行执行效率,分别使用100 M、500 M、1 G和2 G这4个数据集,在节点个数为1、3、5的Hadoop集群上聚类5次,取其平均运算时长,计算加速比。结果如图3所示。 图3 改进算法在不同数据集下的加速比 根据图3可知,由于100 M的数据集相对较小,在集群的节点为2时,算法的加速比有所提升,此时,数据处理时长超过节点间的通信时长;当集群节点为3时,算法的加速比趋于平稳,说明此时集群资源的利用率最高;然后随着节点数目的不断增加,加速比略有下降,说明此时处理数据的时间要小于节点间的通信时间,集群资源得到浪费。对于500 M、1 G、2 G这些数据规模较大数据集来说,随着节点数目的增加,算法的加速比呈现上升状态,并且由数据规模为500 M的加速比变化曲线可以看出,随着节点数目的不断增加,加速比增长的幅度在逐渐变小。由此可以看出改进后的Canopy-K-means算法在并行化执行时能够有效提升聚类效率,并且数据量越大时算法的效率越高。 本文通过引入“最大最小原则”来优化Canopy中心点的选取,进而定义深度指标计算公式,计算得到最佳的Canopy个数及区域半径,避免了传统Canopy算法初始阈值人为指定的问题;接着借助三角不等式定理对K-means算法进行优化,减少冗余的距离计算,加快收敛速度;最后结合MapReduce分布式框架将改进后的算法并行化实现,在构建的微博文本数据集上进行实验,结果表明改进算法的准确率和扩展性都得到提升。但是,由于Canopy中心点的计算花费时间较长,如何在保证聚类准确度的同时,提高Canopy中心点的生成效率还有待研究。3 实验与分析
3.1 实验环境及测试数据集
3.2 实验结果与分析


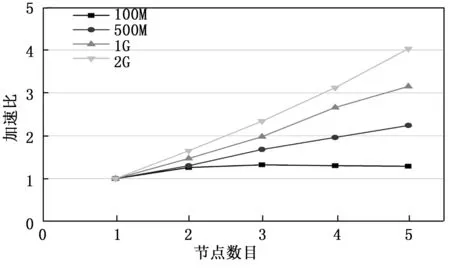
4 结束语

