基于模糊神经网络的涡喷发动机控制系统设计

李慧琳，封 锋

(南京理工大学 机械工程学院，南京 210094)

0 引言

近年来，微型涡喷发动机在微型无人机、巡航导弹、小型靶机上得到越来越多的应用[1]，发动机ECU控制系统作为整机控制的心脏对于涡喷发动机能够精确且快速地达到所需工作状态具有决定性作用。微型涡喷发动机ECU控制器主要功能是根据接收到的控制指令对涡喷发动机的供油量mf进行控制，同时通过数据采集系统从发动机上拾取发动机的转速n、推力F，并结合发动机当前的状态系数对发动机进行闭环控制。在ECU中，转速不仅是系统的输出量，同时也是系统控制的控制信号，因此需要ECU控制系统能够快速准确地输出系统转速，并且在遇到干扰时具有良好的鲁棒性。

目前，PID控制方法由于其算法简单，易于实现的优点已经被广泛应用于各种控制领域[2]。但涡喷发动机转速控制系统为非线性系统，传统PID控制在非线性系统中的表现并不良好。因此采用模糊控制来弥补传统PID控制无法在线调参的不足。

为进一步提高模糊PID控制系统的性能，有学者将遗传算法和BP神经网络应用于模糊控制中，虽然解决了难以将控制参数调至最优的问题，但仍存在训练时间长的问题。本文采用模糊神经网络控制方法，很好地解决了模糊控制和神经网络单独使用时的弊端，提高了PID控制系统的性能。利用Simulink仿真将3种控制系统应用于ECU控制系统进行仿真，结果显示模糊神经网络PID的系统稳定时间最快，超调量最小，在遇到干扰时鲁棒性最好。

1 控制系统的数学模型建立

微型涡喷发动机ECU控制器的控制系统由多个控制部分组成，其中转速控制部分尤为重要。由于转速与发动机的供油量有关，同时又能反映系统的输出推力，因此采用发动机的供油量-转速数学模型作为控制模型进行设计。

涡喷发动机建模普遍采用部件法建模的方式，但该方法过程复杂，为降低系统的建模时间和建模难度，本文采用系统辨识方法建立涡喷发动机控制系统模型。系统辨识方法是一种黑箱建模问题，即利用系统的输入输出数据，在系统结构和参数无法获得的情况下，通过系统的一组实测输入输出数据，根据一类系统模型辨识出被测系统的等价数学模型。系统辨识的基本原理即基于系统对象的输出u(t)和建立的模型对象(t)的差，调整被建立模型的参数，通过逐次逼近的方式，迭代消除误差，最终获得系统的输入输出变量之间的等价数学模型[3]。系统辨识的基本原理如图1所示。

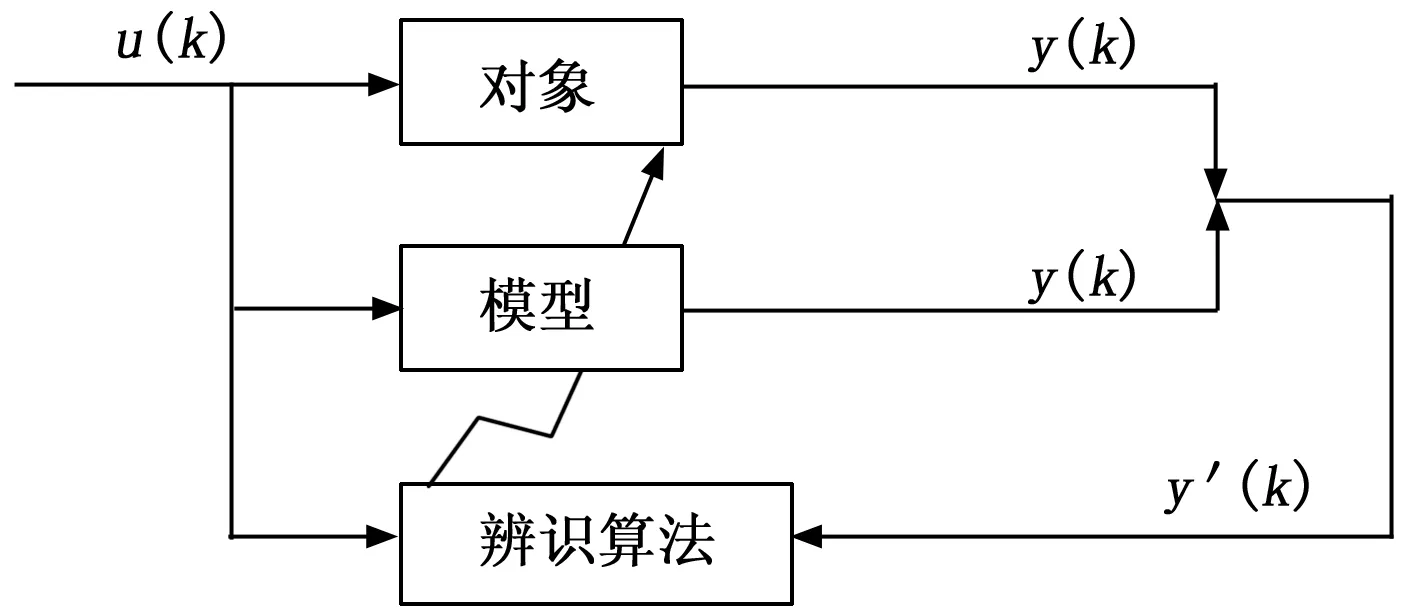
图1 系统辨识的基本原理图

本文将涡喷发动机的供油量作为系统的输入，发动机的转速n作为输出，利用系统辨识工具箱进行辨识[3]。辨识模型选择二阶延迟为1的模型，通过对多种迭代方法的对比分析，采用Adaptive Gauss-Newton迭代法。

经过辨识验证二阶有延迟模型辨识得到的结果基本贴近原始数据，拟合度达到94.34%，得到的系统数学模型为：

(1)

2 PID控制系统的设计

2.1 传统PID控制系统设计

PID控制器的工作原理是将设定的目标值与实际输出间偏差e(t)的比例、积分、微分计算结果通过线性组合生成的控制量u(t)应用于被控系统进行控制[4]，控制量u(t)的表达式如下：

(2)

传统PID控制的传递函数公式为：

(3)

从式(2)、(3)中可以看出，PID控制器输出的控制量u(t)与比例系数KP、积分系数KI、微分系数KD有关，因此在PID控制系统中对以上3个参数的调节对系统性能影响很大。这3个参数的整定规则如下：

1)比例系数KP用于调节系统的偏差。加大比例系数能提高系统的调节速度，但过大的比例系数同样会造成系统稳定性下降。

2)积分系数KI用于消除系统的稳态误差，KI越小积分作用越明显，积分作用的适度加入能够减小系统的稳态误差，但也会减慢系统的响应速度。

3)微分系数KD用于改善系统的动态性能，及早地预见系统的偏差，对误差进行及早控制，但不当的微分调节也会放大系统的干扰因素，增加超调时间。

因此选择合理的PID控制参数是PID控制系统至关重要的部分。本文利用试凑法[5]对比例系数KP、积分系数KI、微分系数KD进行整定，首先只在系统中加入比例系数KP，当系统的响应接近稳态时逐渐加入微分单元系数KD，对三参数按照上述的规则进行调试直到系统输出满意的结果为止，本文经过试验最后得到的参数分别为KP=300，KI=20，KD=45，传统PID控制器结构如图2所示。

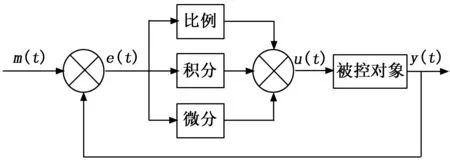
图2 传统PID控制器结构图

2.2 模糊PID控制系统设计

模糊PID的控制原理即利用模糊控制规则对PID控制参数进行在线调整。模糊控制器的输入为转速误差e和转速误差变化率ec，由于模糊控制器是一种语言型控制器，因此需要将输入变量转换为语言变量即模糊化，但在控制器中实际输出均为清晰量，因此还需要对疏忽粗的模糊量进行清晰化处理，最后输出ΔKP、ΔKI、ΔKD。模糊PID控制结构如图3所示。其与传统控制器的区别在于模糊控制模块的加入。

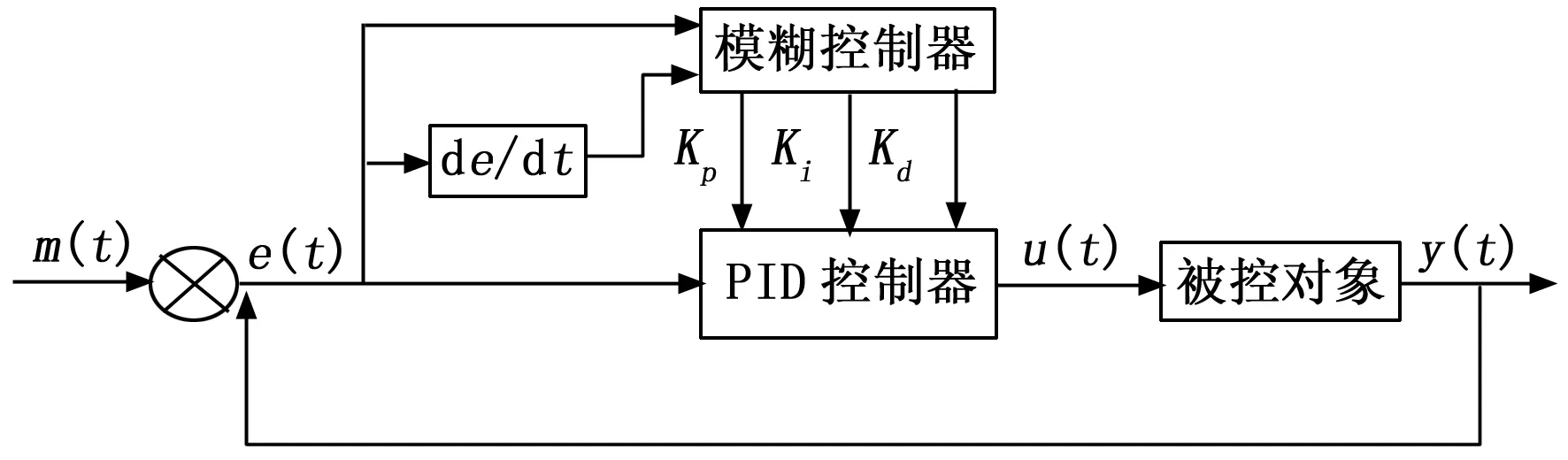
图3 模糊PID控制结构图

本文采用Mamdani型模糊控制器进行仿真，隶属函数选择三角形隶属度函数[6]。模糊PID控制器的设计步骤如下：

1)输入输出变量的物理论域：误差、误差变化率、输出控制量的物理论域为[-3，-2，-1，0，1，2，3]。

2)量化因子：误差、误差变化率的量化因子为3/e。

3)比例因子：输出控制量u的比例因子W1、W2、W3=u/3。

4)模糊子集：本文取e、ec和u的模糊集均为[NB，NM，NS，ZO，PS，PM，PB]，分别代表负大，负中，负小，零，正小，正中，正大。

5)模糊控制规则:根据表1的模糊规则对PID参数进行调节，最终将模糊控制输出的ΔKP、ΔKI、ΔKD与KP、KI、KD相加得到最终的PID控制参数作为控制系统的输入控制变量，最终得到的模糊PID控制的输出为KP′=KP+ΔKP，KI′=KI+ΔKI，KD′=KD+ΔKD[7]。

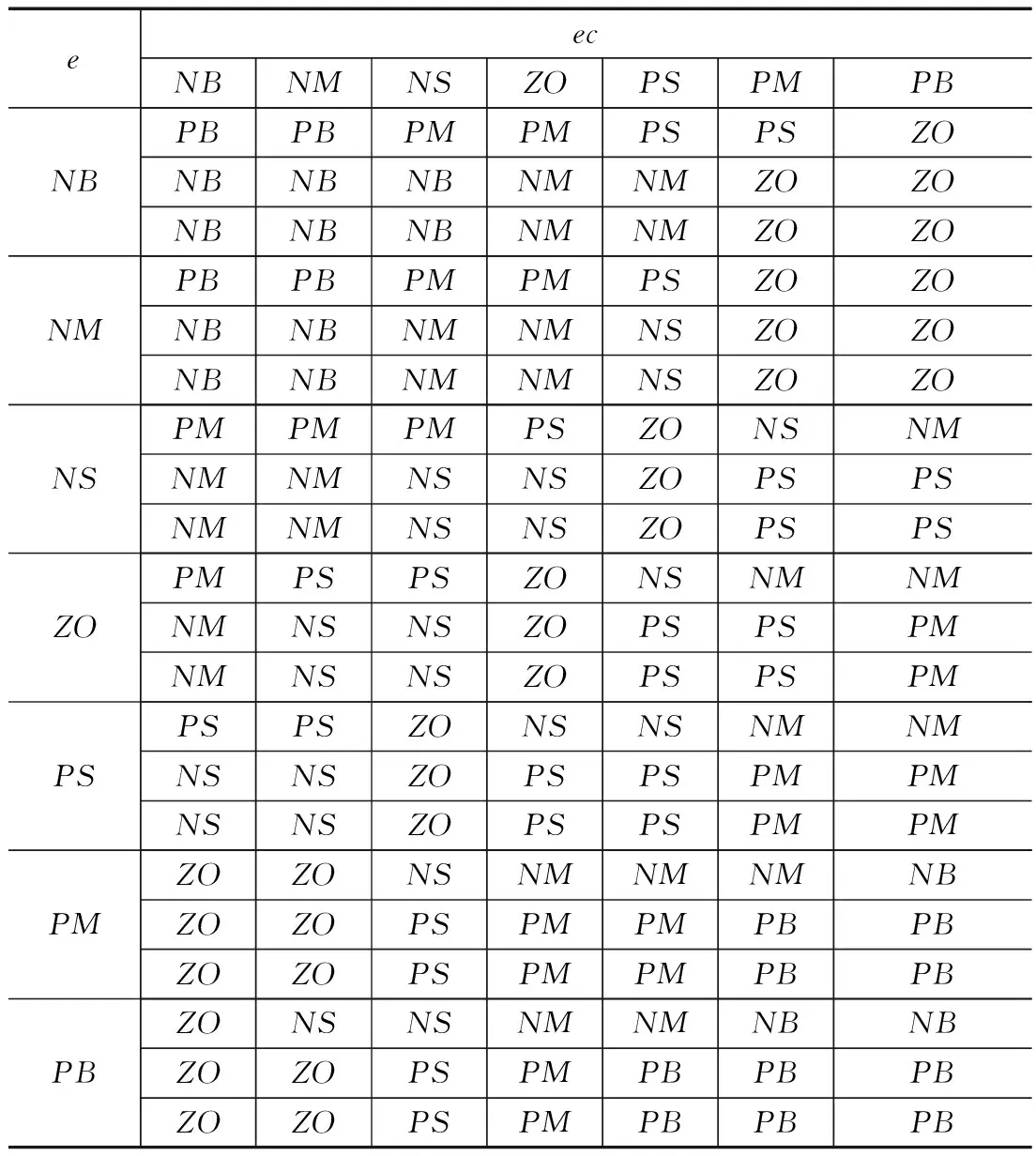
表1 ΔKP、ΔKI、ΔKD模糊规则

2.3 模糊神经网络PID控制系统设计

2.3.1 模糊神经网络系统设计

模糊神经网络控制即用神经网络对模糊规则进行学习，用神经网络学习得到的模糊规则和相应的隶属度函数来代替模糊控制中由人为总结的操作经验规则，弥补了模糊控制缺乏在线学习和自我调整的能力[8-9]。微型涡喷发动机ECU模糊神经网络共有5层，其结构如图4所示。

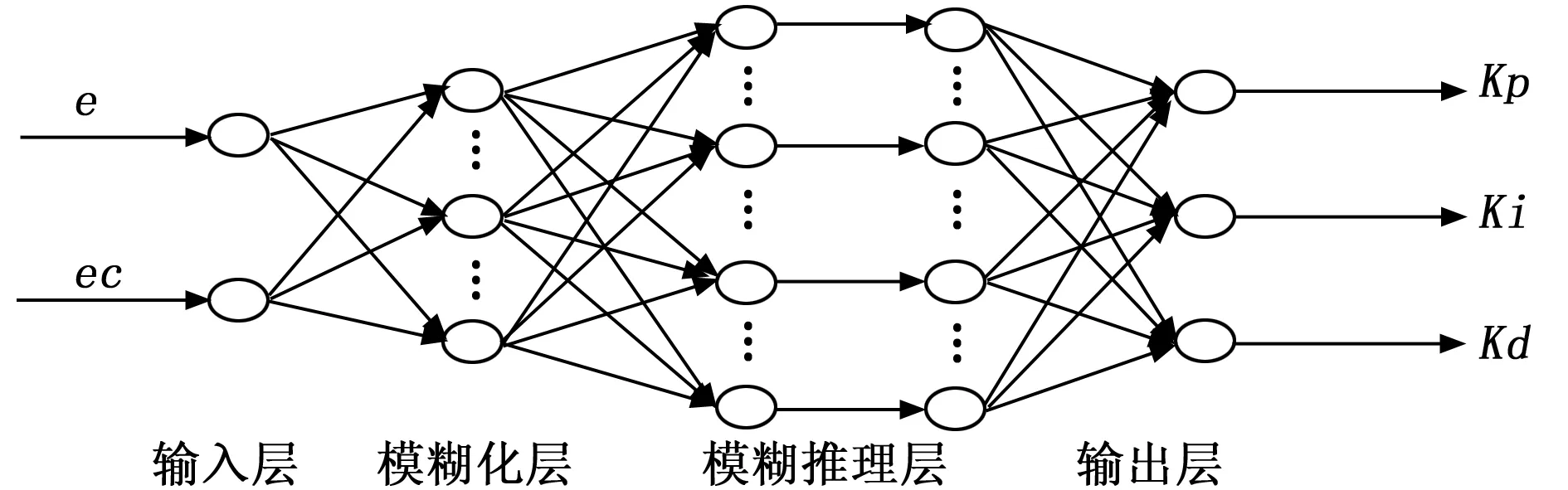
图4 模糊神经网络结构图

本文采用的模糊神经网络系统如图5所示，它采用多层前向神经网络，每层完成一个特定的任务，然后将信息传递至下一层。

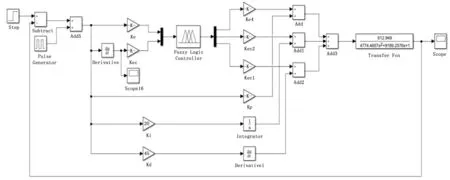
图5 模糊神经网络PID仿真模型

第一层接受系统的输入量e和ec，共两个输入结点。

第二层完成模糊化，每一个节点表示一个语言变量值，对应的有7个语言变量值即模糊集，如NS、NM，该层共有7个结点。用于将e和ec模糊化，利用三角形隶属度函数f(x)分别计算出这两个变量隶属于各个模糊集的程度。输出为：

(4)

式中,a、c为输入变量的变化范围，b为中心值，x即为输入量e和ec，f(x)的值越大，相应的隶属度就越高。

第三层为模糊推理层，每个结点代表一条模糊规则，共有49条模糊规则。该层每个结点的输出为所有输入的乘积。输出为f(e)·f(ec)。

第四层中对第三层的数据进行归一化。

第五层完成清晰化将控制量输出，即输出KP、KI、KD。

2.3.2 模糊神经网络学习训练

本文采用有导师学习方法Delta(δ)对样本数据进行训练学习，具体训练步骤即根据实际输出与理想输出的差E来调节权值ω，对每个样本反复进行上述过程，直到实际输出与理想输出的误差达到设定范围。误差函数：

(5)

式中,dp-yp即实际输出与理想输出的差，其中yp为实际输出与权值ω有关。采用梯度下降法，通过不断调节权值ω使E逐渐减小，直到E减小到小于设定目标数值。

学习训练系统的输入变量为转速偏差e和转速偏差率ec，输出变量为Kp、KI、KD。将其模糊语言变量NB，NM，NS，ZO，PS，PM，PB分别转换为物理量-3，-2，-1，0，1，2，3。利用Matlab中的anfisedit工具箱对上一节中提供的Kp、KI、KD控制规则学习样本进行学习。设定学习误差E为10-4，经过学习训练拟合误差约为10-6,小于设定值10-4。

3 实验结果与分析

利用Simulink将上文中设计的传统PID、模糊PID和模糊神经网络PID控制算法应用于涡喷发动机ECU转速控制系统模型进行仿真实验，模糊神经网络PID仿真模型如图5所示。

采用转速为50 000 r/min阶跃信号作为系统的输入信号，通过与实际输出转速y(t)作差得到控制系统输入误差e和误差导数ec，经过神经网络PID控制器后输出发动机控制系统的控制变量供油量mf，将其输入控制模型，得到仿真结果如图6所示。

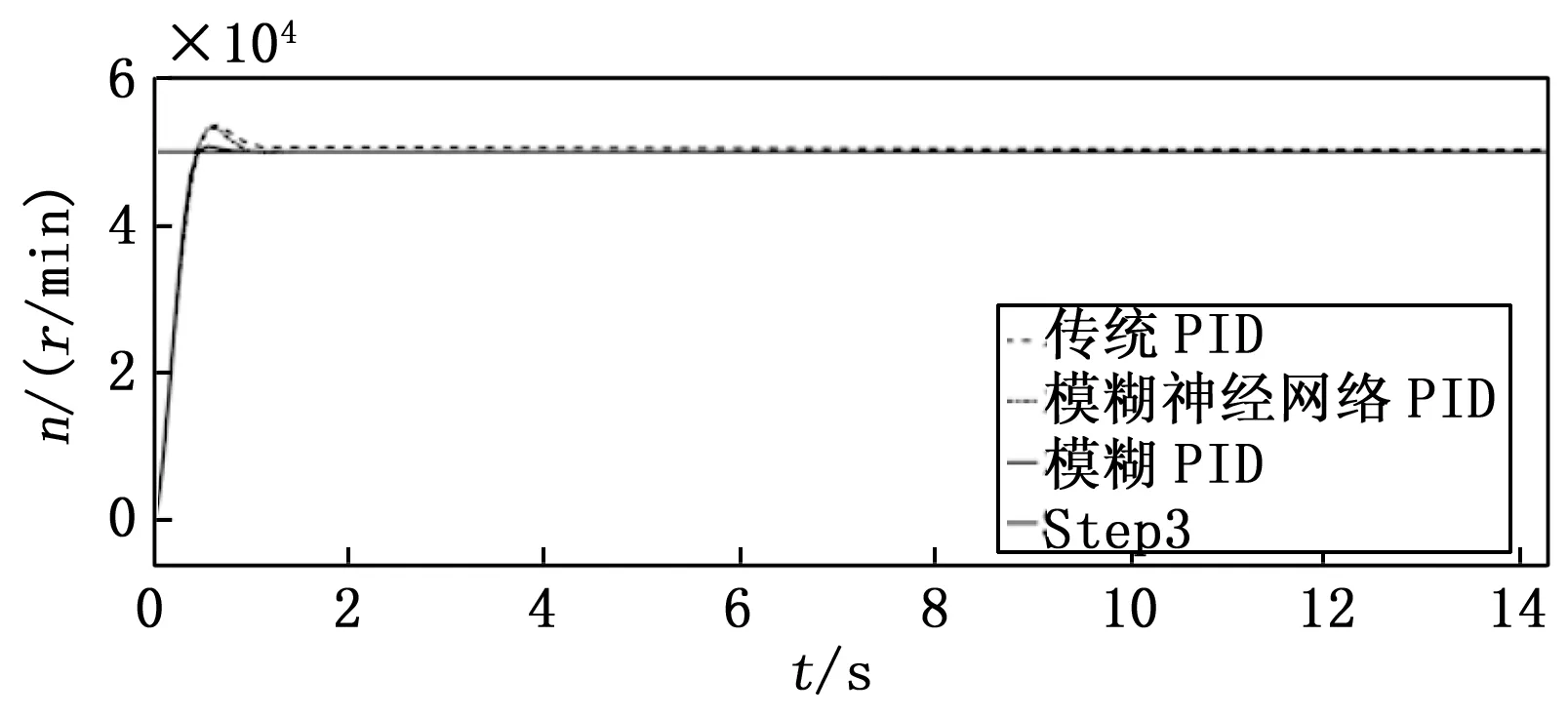
图6 阶跃响应仿真对比图

从图6可以看出在未对系统加入干扰时，传统PID、模糊PID和模糊神经网络PID三种方法的响应时间基本相同，但模糊神经网络PID控制的超调量最小，稳定时间最快。其中模糊神经网络PID控制的超调为0，响应稳定时间为1 s，而传统PID的稳定时间约为1.6 s。

为了验证在受到干扰时控制系统是否能保持良好的鲁棒性，在仿真进行到10 s时加入了一个50 000的方波信号作为干扰信号来观测系统的抗干扰能力，通过仿真得到结果如图7所示，将结果总结如表3所示。

图7 加入干扰后响应仿真对比图

图7中的仿真数据整理如表2所示，从表2中可以看出，在系统遇到干扰信号时均产生了不同程度的超调。从图7可以看出，模糊神经网络PID控制下的ECU转速控制系统在遇到干扰时调整回稳定状态的时间最快，约为0.5 s，且在遇到干扰时系统的峰值最小，能快速地使系统稳定，可以看出利用模糊神经网络PID的控制效果最好。

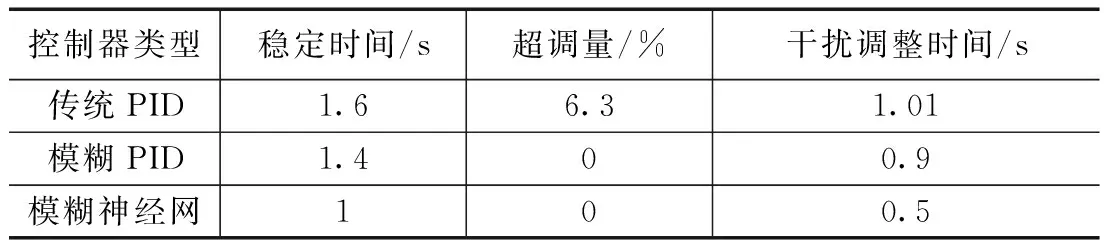
表2 控制器仿真性能指标

微型涡喷发动机ECU控制器最终要实现通过控制系统的供油量来反映系统的推力输出。涡喷发动机推力的大小主要与发动机涡轮前燃气温度、压气机增压比、涡轮效率和压气机效率有关，这些因素的变化均与发动机转速有关，在发动机转速增加时，空气流量和单位推力都会逐渐增加，发动机推力也随转速增加而增加。因此利用输出的转速大小来反映系统的推力输出大小。

通过采集的转速、推力实验数据，利用BP神经网络辨识方法对二者之间的关系进行辨识，采用输出可以取任意值的线性函数pureline作为输出层的传递函数，经过BP神经网络对实验数据的迭代学习最终得到转速-推力关系模型[10]。该模型能够直观地表示转速与推力的数学关系，将其应用于ECU控制系统，仿真模型如图8所示。该模型即将模糊神经网络输出的转速信号作为输入信号输入转速-推力模型，输出发动机推力。

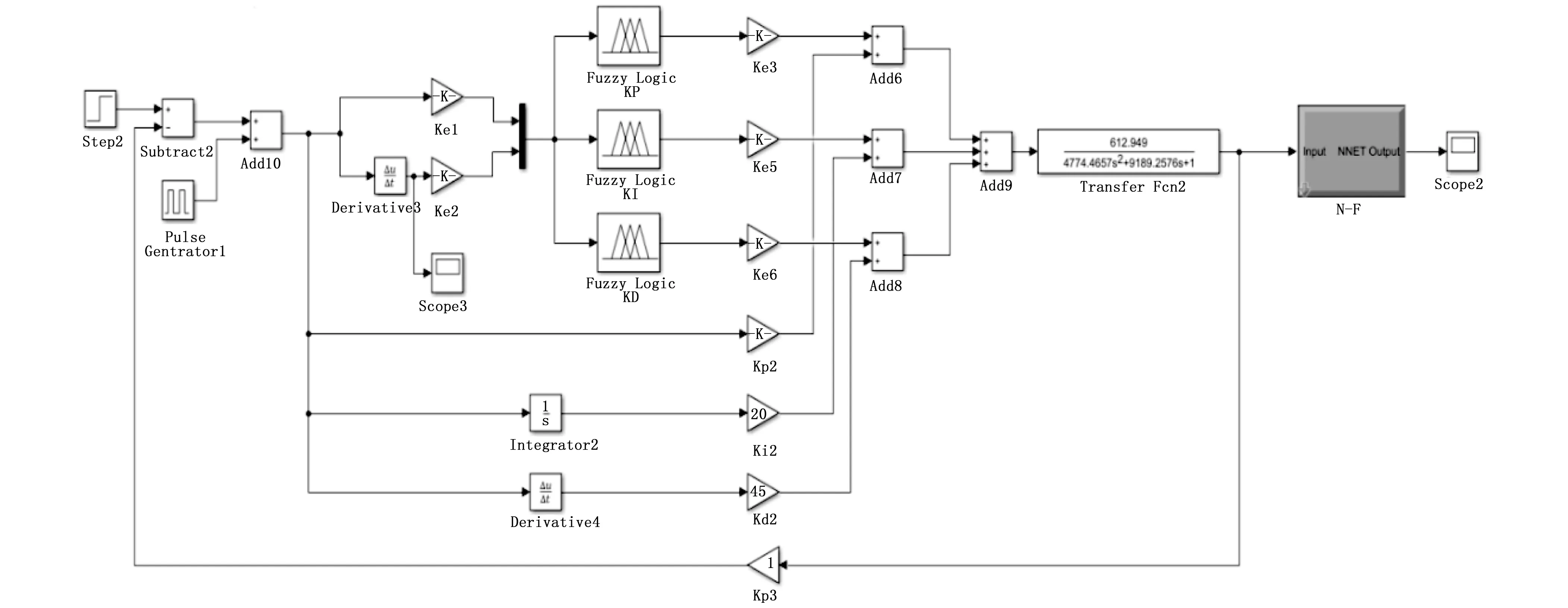
图8 ECU控制系统仿真图

利用转速与推力之间的关系来间接反映输出推力的大小，仿真结果如图9所示。

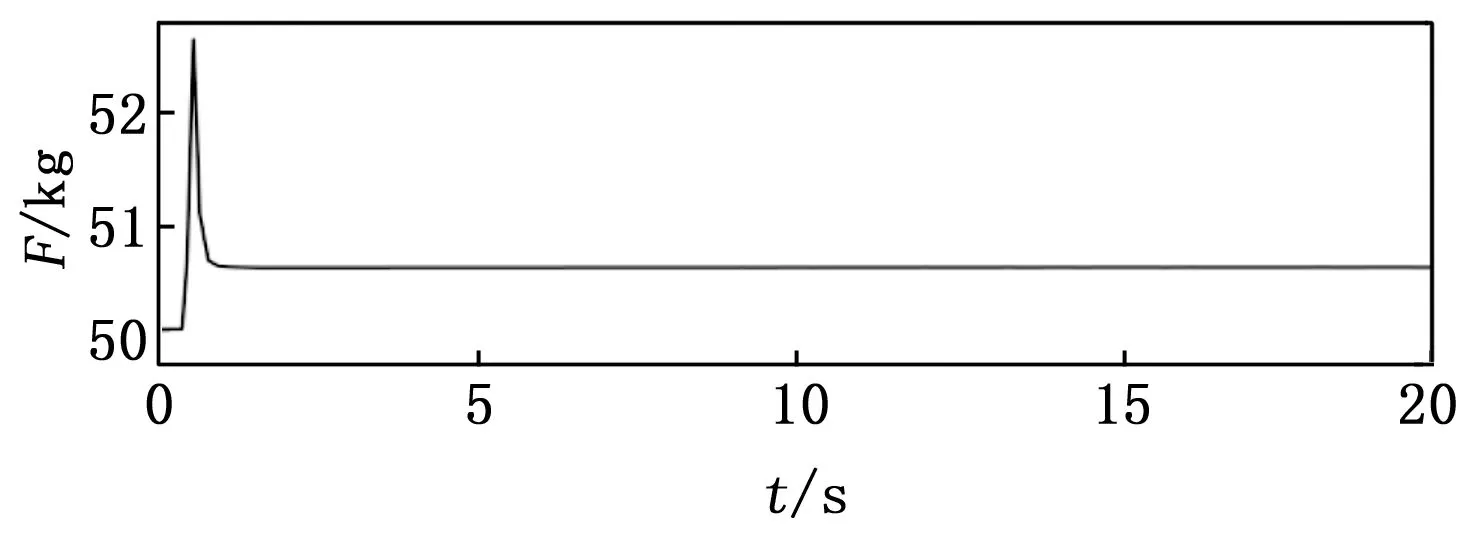
图9 推力输出曲线

从图9可以看出，根据转速-推力关系输出的推力基本与理论数据吻合，以转速48 000 r/min为输入，仿真结果输出的推力为50.6 kg与理论推力输出50 kg相差0.6 kg，该误差的产生主要为辨识模型与实际输入输出数据之间存在误差，仿真模型误差不大。系统从响应到稳定的时间约为1 s与模糊神经网络控制器的响应时间基本相同，由此可以看出模糊神经网络PID控制器在微型涡喷发动机ECU控制系统的应用是可行的，不仅实现了涡喷发动机系统转速的控制，同时还通过转速反映了输出推力的变化，间接的实现了对发动机输出推力的控制。

4 结束语

由于涡喷发动机的具体结构数据较难获得，传统的部件法建模在未知发动机结构参数情况下难以应用的问题，本文利用某微型涡喷发动机的实验数据通过系统辨识的方法前后获得了某微型涡喷发动机的供油量-转速与转速-推力数学模型，从一定程度上减轻了系统建模的复杂度，缩短了系统建模的时间。利用对模型精确度要求不高的PID控制方法来设计控制系统。

为弥补传统PID控制的不足，将模糊神经网络算法与传统PID相结合，利用神经网络的学习能力与模糊控制相结合的优点，使得控制器在线调参的能力得到进一步提升，减小了控制系统响应的超调量，增强了系统的鲁棒性。使系统性能得到了一定的提高。

为了能够实现对微型涡喷发动机的输出推力的监测，采用BP神经网络辨识方法模拟了输出转速与推力之间的关系，在拟合误差不大的情况下，将其加入模糊神经网络PID控制仿真模型中，最终得到了与实际输出误差不大的推力输出，从一定程度上反映了推力随转速的变化规律，实现了微型涡喷发动机ECU转速控制系统的基本控制功能，在控制性能上也得到了一定的提高。