往复式密封流变特性的分析与验证∗
袁 祥, 王 军, 廉自生, 王国法, 马 琳
(1.太原理工大学机械与运载工程学院 太原,030024) (2.天地科技股份有限公司开采设计事业部 北京,100013)(3.山西省生态环境研究中心 太原,030024)
引 言
液压往复密封作为工业、汽车、航空航天和医疗等领域的关键机械元器件,在工业生产中起着至关重要的作用。作为执行机构的密封元件,密封一旦出现泄露,轻则污染环境,给施工带来困难,重则引起安全事故,例如,1986年美国航空航天局航天飞机的灾难就是由于O 形密封圈的失效造成的。
19 世 纪40年 代,White 等[1]发 表 了 关 于 往 复 密封的理论与实验研究,关于密封的研究首次取得突破性进展。Kanters 等[2]和Nikas 等[3]通过实验对往复式密封的摩擦和泄露进行了测量,并对密封机理进行了分析。Zhang 等[4]采用有限元分析方法研究了O 形环的工作应力分布和破坏机理,并给出了密封的失效准则。谭晶等[5]利用ANSYS 分析了密封参数以及安装尺寸对密封性能的影响。胡殿印等[6]通过建立火箭发动机O 形圈的轴对称模型,分析了其应力分布规律。文献[7-9]综合考虑粗糙度和接触力学模型,对密封接触区的压力、膜厚、摩擦力和泄漏量等因素进行了分析。文献[10-11]在Salant等[9]的基础上,提出了一种偏心和拉伸的三维模型,研究了平行偏移和拉伸对密封微观和宏观性能的影响。Öngün 等[12]以ABAQUS 软件为基础,建立了O形圈密封界面的混合润滑理论模型,通过仿真验证了模型的准确性。蔡智媛等[13]利用ANSYS 建立了O 形密封圈的轴对称模型,通过分析安装尺寸和操作参数对密封圈应力的变化规律,获得轴端安装结构的参数最优值。以上研究主要采用有限元软件优化安装尺寸、结构参数或分析密封界面的接触应力,对密封机理的评价不够精确。
为了更准确地反应往复式密封的密封机理,笔者采用弹性变形理论,基于混合弹流润滑模型建立数学模型,进一步分析了介质黏度、密封表面粗糙度以及密封杆速对密封机理的影响规律,为工程设计以及应用提供了一定的指导。
1 数学模型
密封圈未安装状态、安装状态和密封与杆处于混合润滑状态时的微观接触图如图1 所示。密封主要依靠密封圈的径向压缩产生高接触压力以及高压流体压缩后的弹性回弹作用。由图1(b)可以看出,根据密封杆的运动方向不同,可将行程分为进行程和出行程。前者表示缸体排油动作,后者为吸油动作。图1 中:h为沿径向的油膜厚度;L为整个密封区的接触宽度;xo为密封初始点横坐标;xl为密封终止点横坐标;psc为密封接触压力。笔者对油膜比厚λ[14]定义为λ=h/σ,其中:h为油膜厚度;σ为均方根(root mean square,简称RMS)粗糙度。当油膜比厚0≤λ≤3 时,代表密封接触区处于混合润滑状态,此时的载荷由流体运动产生的流体压和微凸体[15]产生的粗糙接触压力共同承担。当λ≥3 时,密封区域为全膜润滑状态,此时的接触压力全部由流体压力承担。在密封圈的实际应用过程中,大部分处于混合润滑状态[16-19]。因此,笔者将基于混合润滑状态展开讨论。
1.1 流体分析模型
与密封接触区长度相比,接触区油膜厚度h一般处在微米级别,因此往往忽略因油膜厚度引起的变形。笔者假设密封介质为不可压缩性的牛顿流体。当密封圈的表面粗糙度小于密封杆的1/10 时,可认为密封杆的表面是绝对光滑的[2]。密封界面的油膜厚度与流体压力之间的关系可用Patir 等[18]修正的一维雷诺方程表示
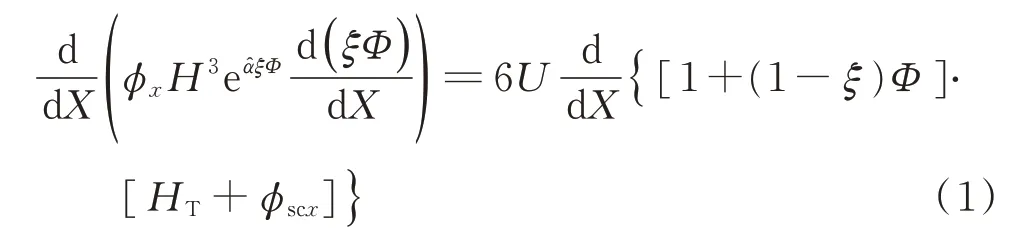
其中:所有参量均为无量纲,x为沿杆运动方向的坐标;黏度和压力之间的关系服从Barus[20]黏压关系μ=μ0eαp;α̂=αpa;φx,φscx分别为压力流量因子和剪切流量因子[2,18];H为沿接触方向的油膜厚度;HT为平均局部油膜厚度;U为杆的运动速度;pa为空气侧压力;Φ为流体压力或空化区域内流体密度[21];ξ为空化因子;当Φ≥0 时,ξ=1;当Φ<0 时,ξ=0。
流体压力的边界条件为
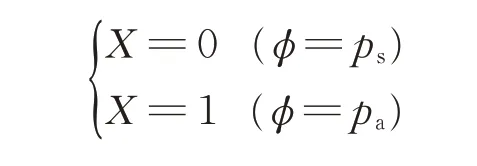
1.2 本构模型
O 形密封圈的材料为丁腈橡胶,由于橡胶材料具有典型的非线性特性,因此笔者将其简化为超弹材料进行处理[22-23]。用于描述超弹材料力学性能的模型通常有3 种:Mooney-Rivlin,Neo-Hookean 和Ogde。其中,Mooney-Rivlin 模型因其与实验匹配性最佳而被广泛采用[23-24]。丁腈橡胶材料通常被视为具有不可压缩性的超弹性材料,在ANSYS 分析中,笔者将其力学模型选取为Mooney-Rivlin 超弹模型[24],取三参数模型进行描述,如式(2)所示,密封杆和缸体则为线弹性模型。宏观变形部分通过ANSYS 进行仿真,接触对选取TARGE169和CONTA172,网格划分为精细网格。
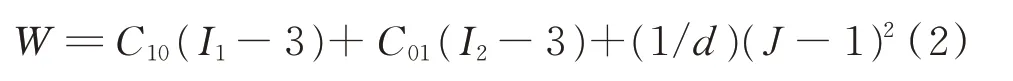
其中:W为应变能密度;C10,C01为材料常数,C10=0.43295 MPa,C01=1.51508 MPa;I1,I2为Green-Lagrange 应变不变量;J为材料体积率;d为材料体积变化率,d=0.001027。
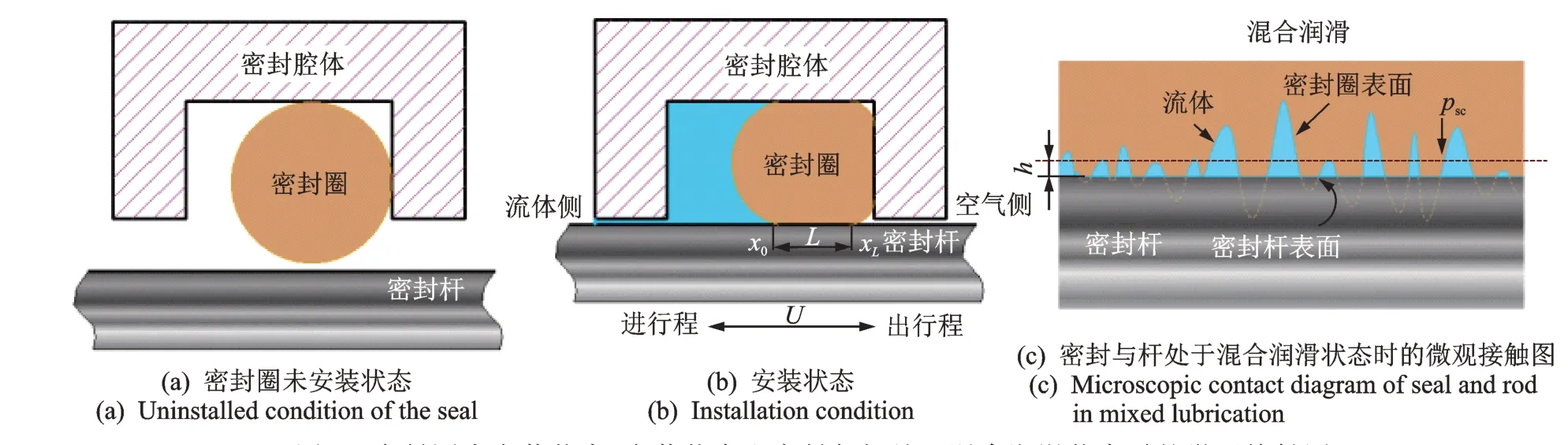
图1 密封圈未安装状态、安装状态和密封与杆处于混合润滑状态时的微观接触图Fig.1 Schematic diagram of the uninstalled condition, installation condition and microscopic contact diagram of seal and rod in mixed lubrication
1.3 接触模型
考虑到油膜比厚的范围为0≤λ≤3,密封区间润滑处于混合润滑状态,所以不能忽略此区间应力带来的影响。笔者采用考虑粗糙度和黏性剪应力综合影响的Greenwood-Williamson(G-W)模型[25]为接触模型,每一个接触点遵循Hertz 接触理论,则方程为
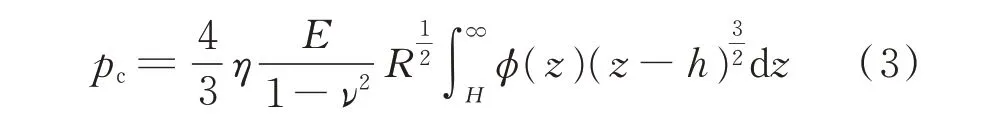
其中:pc为粗糙接触压力;η为微凸体密度;假定粗糙高度服从高斯分布,则R为粗糙半径[26];E,ν分别为密封圈弹性模量和泊松比。
1.4 变形分析
由于密封圈的宏观变形在毫米级别,而微观变形的数量级在微米级别,因此可以忽略计算密封接触界面的微观变形对其宏观变形的影响。笔者采用小变形理论,密封界面任意一点的油膜厚度可用式(4)表示,其中,Iik为影响系数矩阵,可通过离线方程对弹性变量进行求解[27],其弹性变形方程为
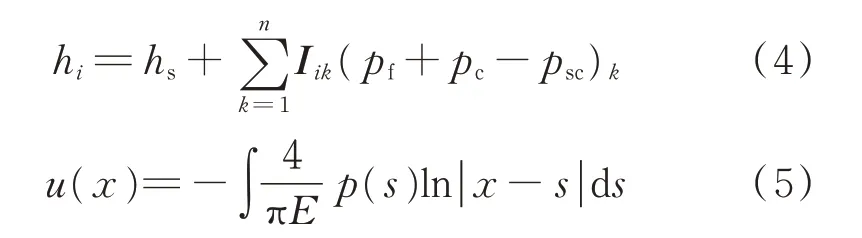
其中:hi为第i个节点的油膜厚度;hs为初始静态油膜厚度;pf为流体压力;psc为静态接触压力;Iik为影响系数矩阵;u(x)为在x处的弹性变形量;s为在x轴方向上的附加坐标;p(s)为在s处的节点压力。
1.5 辅助计算
计算流程图如图2 所示,整个收敛过程是一个迭代计算的过程。
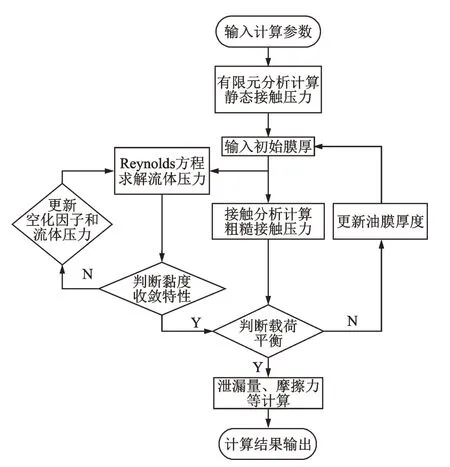
图2 计算流程图Fig.2 Computational procedure
总摩擦力F由黏性摩擦力Ff和粗糙接触摩擦力Fc组成。粗糙接触产生的摩擦力Fc为
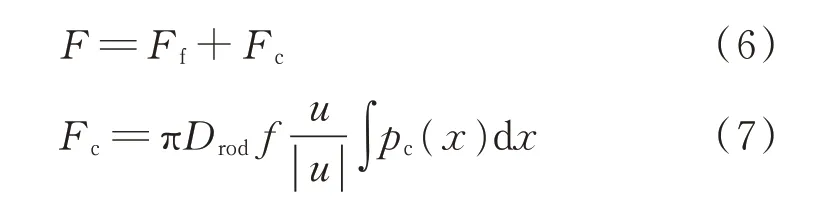
流体黏性摩擦力Ff为
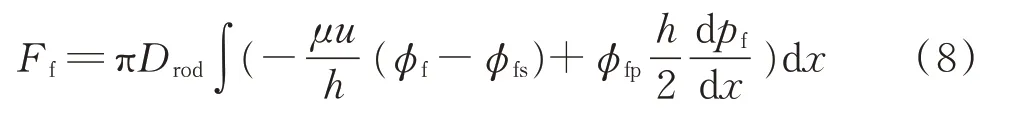
流量q计算公式为
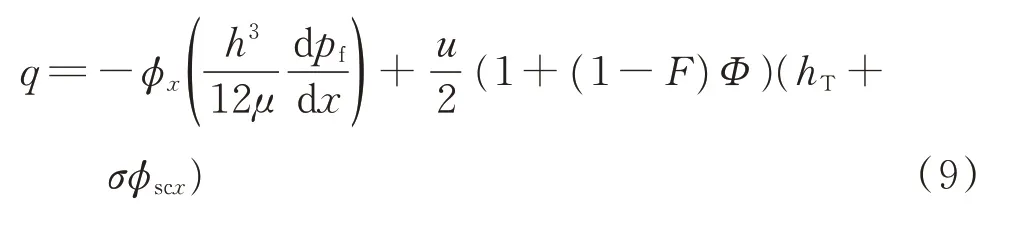
摩擦因数f计算公式为
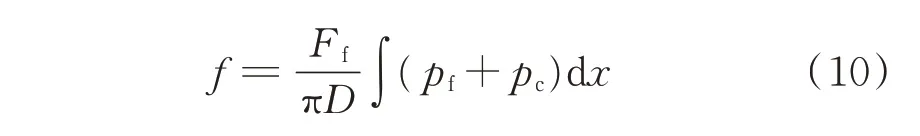
其中:Drod为密封杆的直径;φf,φfs以及φfp均为剪切应力因子[28]。
2 密封性能分析
笔者计算所需参数如下:密封杆的半径Drod=30 mm;有效行程长度L=50 mm;密封圈的截面尺寸dseal=5.33 mm;经验摩擦因数f=0.025。由于杆在出行程过程中密封压力为空气侧压力,因此出行程密封压力pout=0.1 MPa;进行程时,密封压力为密封缸体内部压力,此时的密封压力pin=4 MPa;黏压系 数α=20×10−9/Pa;密 封 圈 的 弹 性 模 量E=16 MPa;密封圈的泊松比ν=0.499;密封圈表面粗糙度在无特殊强调下为0.8 μm。
2.1 粗糙度对密封性能的影响
图3为密封特性随粗糙度和密封杆速度的变化规律。图3(a)为密封圈表面粗糙度σ从0.2~1.4 μm 时的摩擦力与泄漏量的变化规律。在进行程时,摩擦力随着粗糙度的增加先增加后减小,并逐渐趋于稳定,当粗糙度达到一定数值时,摩擦力不再随之增加;出行程和进行程的泄漏量都随密封表面粗糙度的增加而增大。在出行程时,随着密封圈表面粗糙度的增加,摩擦力单调增加后趋于稳定,而泄漏量则和进行程一样,保持单调递增。在粗糙度比较小时,流体动压效应的作用大于粗糙接触的影响,因此摩擦力较小;随着粗糙度的增加,微凸体引起的粗糙接触压力增大而流体动压效应减弱,因此摩擦力逐渐增加。
图3(b)表示在进行程的密封压力为4 MPa 时,密封圈表面粗糙度分别为0.4,0.8 和1.2 μm 时,进行程和出行程的摩擦因数与密封杆运动速度的关系。在不同的粗糙度下,进行程和出行程都存在一个临界速度,当密封杆速度小于此临界速度时,出行程的摩擦因数大于进行程的摩擦因数。出行程的摩擦因数随粗糙度的增加呈现增大趋势;但进行程的摩擦因数因受密封杆的运动速度影响较大,呈现出复杂的变化规律。当粗糙度比较小时,进行程的摩擦因数呈现单调递减趋势,但是随着粗糙度值的增加,进行程摩擦因数的变化趋势呈现出抛物线形状,存在一个拐点。在整个速度变化范围内,虽然进行程的摩擦因数局部存在微小变动,但整体上随着粗糙度的增加而增大。这主要是因为杆速越快,流体动压效应增强,微凸体的粗糙接触压力降低,最终导致接触摩擦力降低。
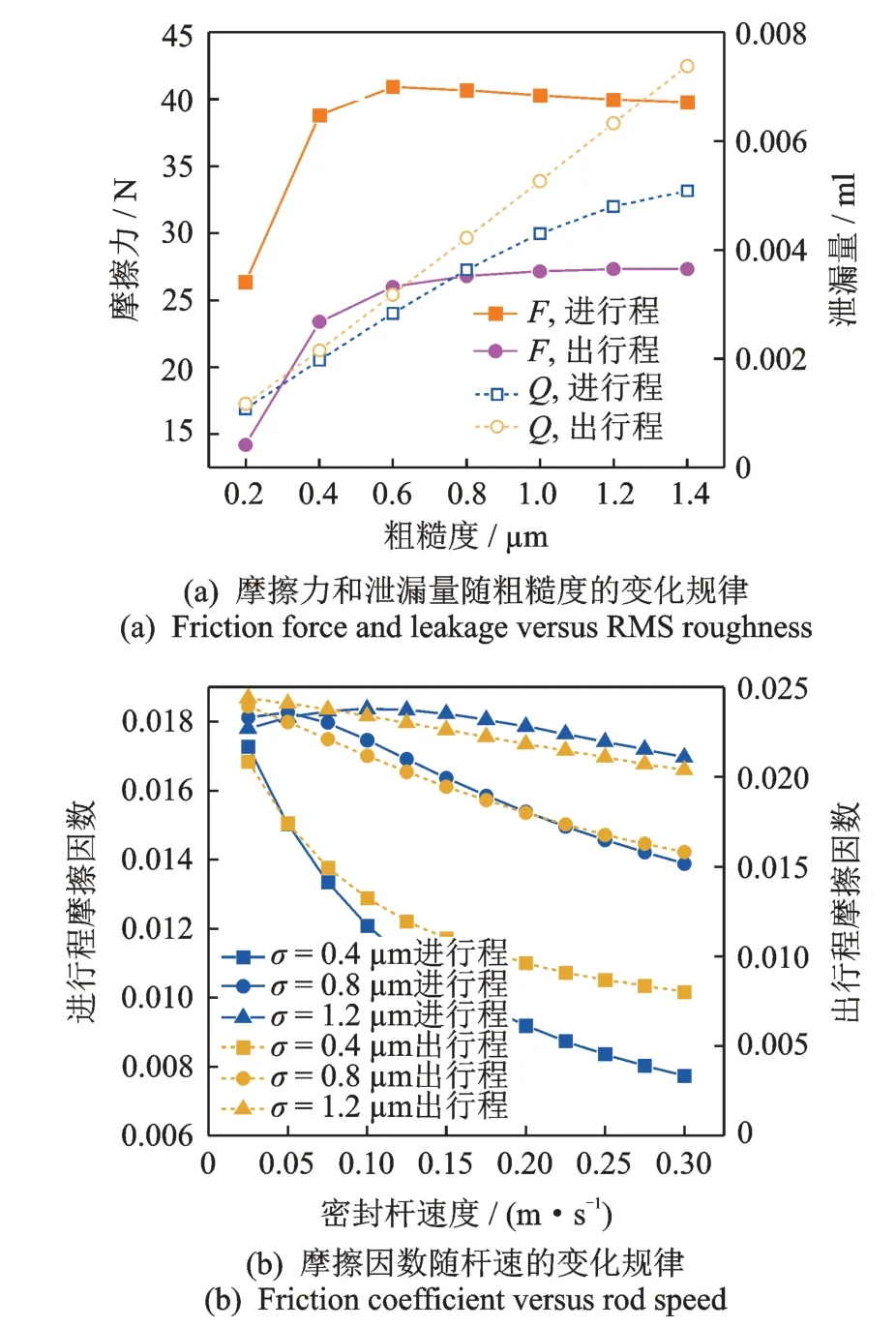
图3 密封特性随粗糙度和密封杆速度的变化规律Fig.3 Seal characteristics versus RMS roughness and rod speed
2.2 润滑油黏度对密封性能的影响
图4 为进行程时,密封压力pin=4 MPa 时,摩擦力随密封杆速度及黏度的变化规律。摩擦力由接触剪应力和黏性剪应力两部分组成。接触剪应力是由密封圈和密封杆的直接接触产生,而黏性剪应力则是由密封圈和密封杆之间的流体产生的。从图4 可以看出,在摩擦力的构成比重中,接触剪应力始终是主要因素,黏性剪应力虽然随着润滑油黏度的增加有所提升,但是仍然不明显。可见,接触摩擦力是产生摩擦力的主要影响因素。
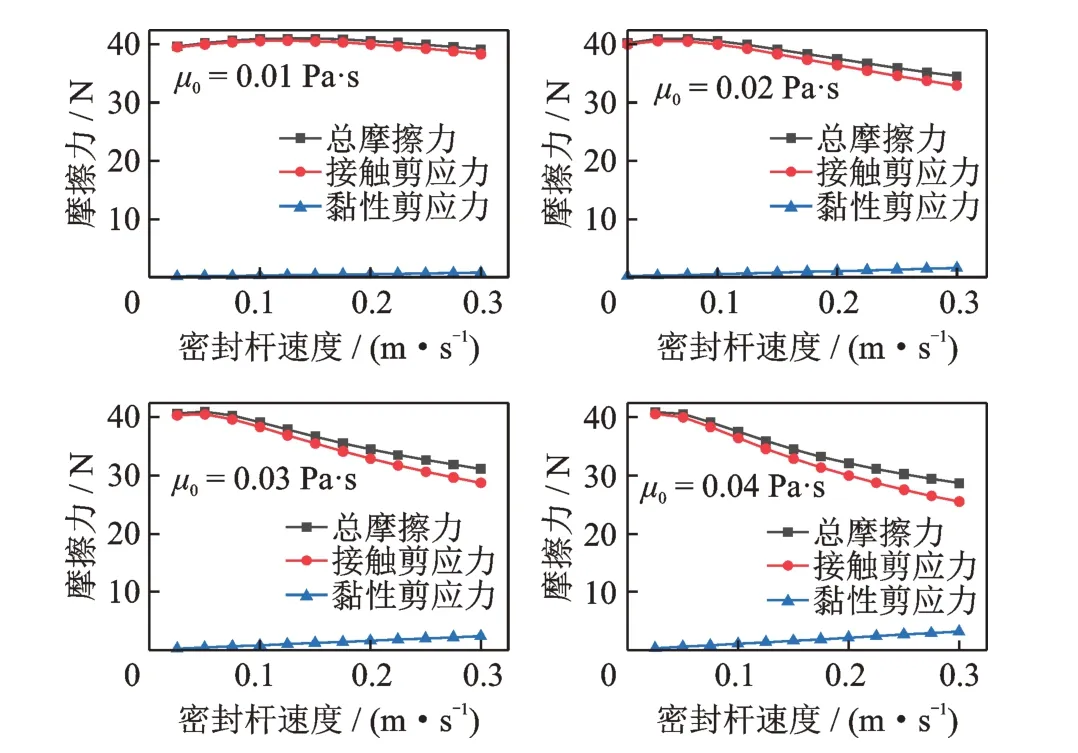
图4 进行程时摩擦力随速度及黏度的变化规律Fig.4 Friction force versus rod velocity and viscosity during the instroke
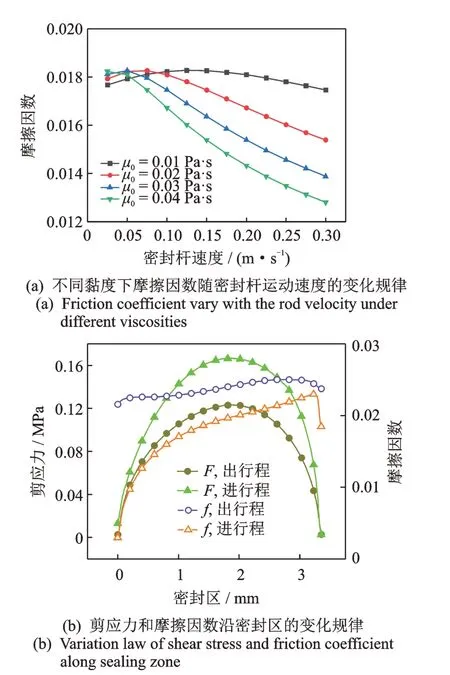
图5 摩擦因数和剪应力随密封杆运动速度及沿密封区变化规律Fig.5 The regulations of friction coefficient and shear stress vary with the rod velocity and along sealing zone
图5 为摩擦因数和总剪应力随密封杆运动速度和沿密封区的变化规律图。5(a)为当|u|=0.025 m/s 和pin=4 MPa 时,在不同黏度下摩擦因数随密封杆运动速度的变化规律。可以看出,摩擦力随着密封杆速度的增加逐渐降低,这是由于密封杆速度越高,引起的流体动压效应越强,密封杆与密封圈接触越少,最终导致接触摩擦力降低。摩擦因数随黏度的变化存在一个临界值,当密封杆运动速度超过此临界值时,摩擦因数随着黏度的增加明显降低,由于润滑油黏度增加,流体剪切摩擦力增加,粗糙接触摩擦力减少而导致总摩擦力降低。从图5(a)中的放大图不难发现,在润滑油的黏度比较低的情况下,摩擦因数随着速度的增加呈现出抛物线的变化趋势,即先升后降;但随着润滑油黏度的增加,这种趋势逐渐消失,最后呈现单调递减的趋势。在运动速度很低时,润滑油的黏度越大,摩擦因数越大;当杆速超过0.09 m/s 时,润滑油黏度越大,摩擦力越小。当润滑油黏度很低时,流体的动压效应不明显且主要克服由于静压效应产生的压力差,因此摩擦因数出现短暂的上升;随着润滑油黏度增大,流体动压效应显著增加,粗糙接触压力降低,导致摩擦因数降低。
图5(b)为当|u|=0.025 m/s 和pin=4 MPa 时,总剪应力以及摩擦因数分别在出行程和进行程过程中沿密封区的变化规律。可以发现,沿着密封方向在出行程过程中的总剪应力明显小于进行程,而摩擦因数的变化则相反,出行程的摩擦因数明显大于进行程的摩擦因数。在出行程和进行程过程中,由于密封压力的不同,导致接触压力大小不一,最终影响了剪应力以及摩擦因数的变化。
综上所述,密封性能受多方面因素的影响,润滑油黏度、密封杆的运动速度以及密封表面的粗糙度等都起着重要作用。在工业应用中,对某一工况来说,一般运行参数确定后不会轻易改变。因此,针对具体的使用工况设计更为合理的密封参数对提高密封性能具有实际意义。研究结果表明:适当增大润滑油的黏度对于降低摩擦力、提高流体的承载能力以及减少材料磨损有着积极的意义;较小的粗糙度能够降低泄露以及减少摩擦;较高的密封杆速有益于降低摩擦力从而减少磨损。
3 实验验证
为了验证笔者提出的数学模型的准确性,设计了一套测试摩擦力的实验装置。密封圈以及密封杆的表面粗糙度是用徕卡公司生产的DM6M 进行测量,密封件被放大1500 倍,测得密封圈的表面粗糙度为0.8 μm,密封杆表面粗糙度为0.072 μm。
3.1 实验测试装置
实验测试原理以及现场实验测试安装图如图6所示。实验设备主要由3 大部分组成:电控部分、液压部分以及信息采集部分。PC 机、电机和变频器构成电控部分;压力传感器、位移传感器以及采集仪组成采集部分;液压部分由液压管路和测试单元组成。测试单元包括缸体、活塞杆、2 个动密封圈和2 个静密封圈。实验装置在充满压力油后保压运行,由此测量的摩擦力由2 部分组成:密封压力下的进行程和密封压力下的出行程。实验测试参数如表1所示。
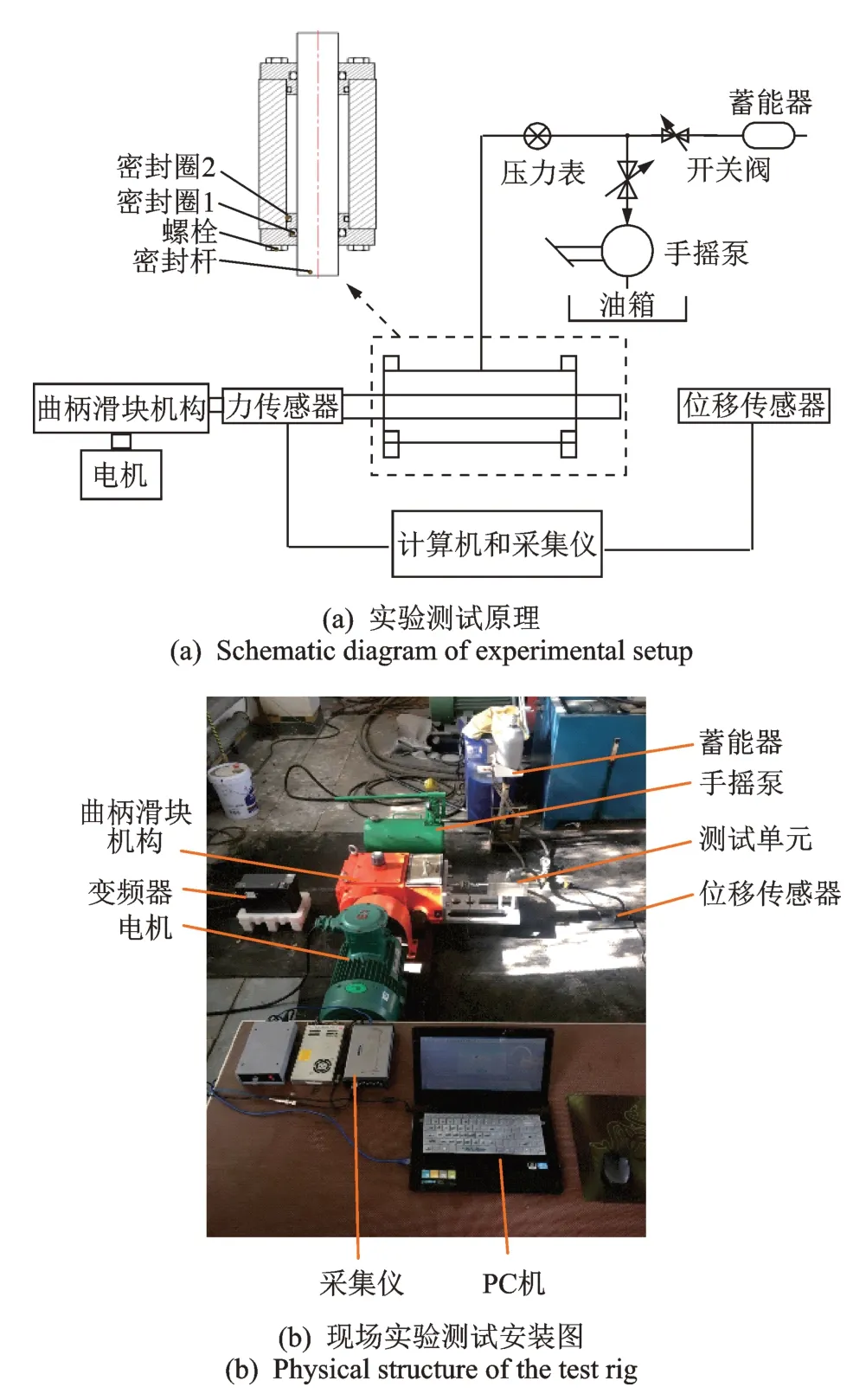
图6 实验测试原理以及现场实验测试安装图Fig.6 Schematic diagram of experimental setup and physical structure of the test rig

表1 实验测试参数Tab.1 Experimental prototype structure parameters
3.2 实验与仿真结果对比
本实验采用的润滑油黏度为0.0396 Pa·s,密封杆运动速度为0.059 m/s,分别在2,4,6 和8 MPa 4种不同的系统压力下对摩擦力进行测量。
图7 为实验测量结果与仿真结果的对比。由于在测量单元中有2 个O 形密封圈,因此实验测试设备记录的摩擦力包含2 部分:密封圈的进行程摩擦力和密封圈的出行程摩擦力。由于测试过程中密封腔内的工作液体一直保压运行,不存在排液过程,因此出行程的密封压力为工作压力。图7 中虚线部分为进行程和出行程在4 MPa 时的摩擦力数值仿真结果,蓝色虚线代表进行程摩擦力;绿色虚线代表出行程摩擦力;红色实线为进行程和出行程摩擦力两者之和;黑色实线为实验测量结果。可以看出,在同样工作压力下,进行程的摩擦力一直大于出行程的摩擦力,且总的摩擦力随着工作压力的增加呈线性增加,此结论与Peng 等[10]的研究结论一致。出现这种现象的原因主要是因为密封压力的增加导致密封圈变形量随之增大,接触长度以及接触应力也相应增大。由于接触摩擦力在总摩擦力中占主要成分,因此测量的摩擦力也随着接触摩擦力的增加而增大。实验结果显示,仿真结果和实验结果的平均相对误差为8.7%,验证了数学模型的准确性。
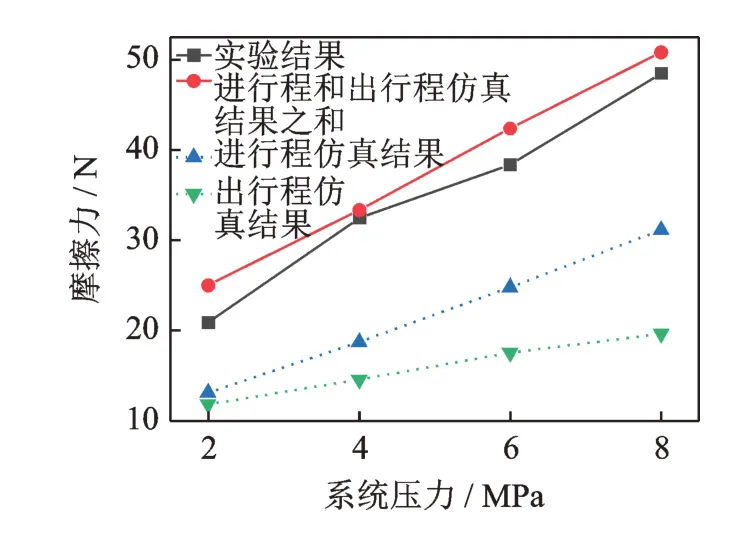
图7 实验测量结果与仿真结果对比Fig.7 Friction force comparison between the test and simulation
4 结 论
1)当密封杆杆速超过0.09 m/s 时,适当提高润滑油的黏度能够明显降低密封圈的摩擦力、提高流体的承载能力以及降低接触摩擦力。因此,合理的润滑油黏度有利于降低接触摩擦副的摩擦力,提高材料的抗磨损性能。
2)高速运动虽然在一定程度上提高了流体动压效应,起到了降低摩擦力的作用,但也增加了流体泄漏的风险。
3)密封接触区处于混合润滑状态,载荷主要是靠粗糙接触来承担,即微凸体的接触分担。因此,表面粗糙度越小,有利于降低摩擦磨损,同时也越有利于减少泄露,防止环境污染。粗糙度精度的提高意味着生产成本的增加,选择合理的表面粗糙度既能在一定程度上降低企业的生产成本,又能有效减少密封材料的磨损,提高抗泄露能力。
4)笔者建立的数学模型是以稳态为前提,而实际润滑油的黏度、密封表面粗糙度以及密封杆的运动速度并不是一成不变的,都随着时间的变化而变化。因此,需要考虑瞬态效应的影响,建立瞬态混合润滑模型,同时还需要对实验测试设备进行相应的改进。

