基于转子故障数据集的KSELF 降维方法∗
户文刚, 赵荣珍
(兰州理工大学机电工程学院 兰州,730050)
引 言
转子故障是旋转机械中常见的故障且危害极大,准确判断转子系统的故障程度和故障类型,对避免重大事故的发生至关重要。通过采集振动信号进行故障检测和诊断是一种应用较广的方法[1-2]。为了获得较高的诊断精度,可以从振动信号时域、频域和时频域等方面提取反映机械设备运行状态的量化特征,但随着特征数量的增多,在故障诊断过程中需处理的特征集维数过高,产生了“维数灾难”问题[3],这加大了分类器的训练时间和空间复杂度。因此,对故障特征集进行非线性维数约简,提取有用的低维敏感特征就显得非常关键[3-6]。
根据是否使用了类别标签,传统的降维方法被划分成2 类:①无监督降维,如主成分分析(principal component analysis,简称PCA)[7];②有监督降维,如Fisher 判别分析(Fisher discriminant analysis,简称FDA)[8]。无监督降维方法由于不能利用标签样本的类别信息,导致最后的分类结果精度不够准确。有监督降维方法虽然能够利用标签信息指导降维过程,避免了无监督降维方法在降维过程中的盲目性,但需要对每个样本进行标记,当训练样本中没有标签样本或者标签样本不足时,其泛化能力会急剧降低[9]。然而,在实际应用中对数据样本进行标记是费时费力的,需要一定的专家知识,而获取大量的无标记样本则相对容易很多。因此,针对无监督降维和有监督降维各自存在的问题,研究仅需少量的标签样本和大量的无标签样本的半监督降维成为降维领域的热点[10-11]。半监督学习可以同时利用少量的标签样本和大量的无标签样本来改善有监督降维方法的泛化能力,提高无监督降维方法的高效性[12]。半 监 督 局 部Fisher 判 别 分 析(semi-supervised local Fisher discriminant analysis,简称SELF)[13]是半监督降维的代表方法之一,能够利用少量标签样本和大量无签样本中的信息指导降维过程,避免了因有标签样本不足引起的过学习问题。但是,SELF 本质上仍是线性降维方法,面对复杂的非线性、不平稳数据,不能保持良好的降维效果。核方法[14]是处理非线性数据的有效方法,能较好解决线性降维方法在处理非线性问题时的不足。
笔者对核方法和半监督局部Fisher 判别分析相结合的故障数据集降维算法进行研究,提出了一种基于核半监督局部Fisher 判别分析的降维方法,为解决高维和非线性机械故障数据集的维数约简与分类问题提供一定的理论参考依据。
1 核方法的概念
核方法[14]是以统计学理论和核技术为基础的非线性数据处理技术的总称,通过运用非线性映射将低维空间中线性不可分的数据映射到高维特征空间,进而在特征空间中实现对应的线性分类。
给定一个数据集X={xi∈RD}(i=1,2,…,n),xi和xj(i,j=1,2,…,n)为数据空间中的样本点,数据空间到特征空间的映射函数为Φ,可直接在特征空间中实现向量内积的变换(xi,xj)→K(xi,xj)=Φ(xi)TΦ(xj),从而达到优化计算和改善算法的目的。常用的核函数主要包括:p阶多项式核函数K(xi,xj)=(xi xj+1)p;高斯核函数K(xi,xj)=线性核函数K(xi,xj)=xi xj;指数核函数K(xi,xj)=
2 核半监督局部Fisher 判别分析
2.1 半监督局部Fisher 判别分析
局部Fisher 判别分析(local Fisher discriminant analysis,简称LFDA)[15]是一种结合了原始FDA 和局部保持投影(local preserving projections,简称LPP)[16]的监督降维方法,克服了原始FDA 针对多模态数据或者异常值的弱点,最大限度地提高了类间的可分性,同时保持了类内局部结构。LFDA 在标签样本不足时,由于过度依赖少量的标签样本容易陷入过学习。为了克服这一问题,Sugiyama 等[13]将LFDA 和PCA 进行有效融合,提出了一种新的半监督局部Fisher 判别分析算法。该方法结合PCA和LFDA 各自的优点,综合考虑有标签样本和无标签样本,使降维后的类间数据距离最大化,类内邻近数据间距离最小化,并尽可能地保持类内非邻近数据。
给定一数据集X,记为X={xi∈Rd×n)},i=(1,2,…,n',…,n),n'为有标签样本的个数。其中:有类别标签样本为xi(i=1,2,…,n');标签样本的类别标签为li∈{1,2,…,c} (i=1,2,…,n')。记类别标签为l的类别中包含nl个样本,则有维数约简的目标就是寻找一个d×r转换矩阵T,使等 式Y=TTX成 立。其 中:Y=[y1,y2,…,yn]∈Rr×n;r(1≤r≤d)为低维空间维度。
SELF 的局部类间散度矩阵和局部类内散度矩阵定义为
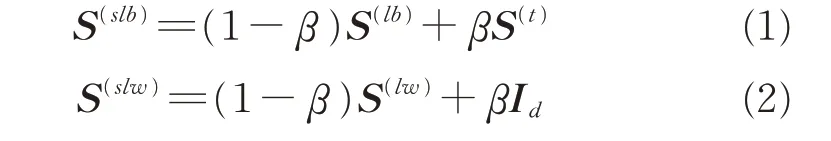
其中:S(lb)和S(lw)为LFDA 定义的局部类间和局部类内散度矩阵,如式(3),(4)所示;S(t)为PCA 定义的全局散度矩阵,如式(5)所示;Id为标准矩阵;β∈[0,1]为权系数。
β使SELF兼具LFDA 和PCA 的特性,可通过调节β的大小来增加算法的灵活性。当β=1 时,SELF 等价于PCA,当β=0 时则等价于LFDA。
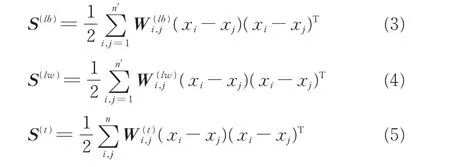
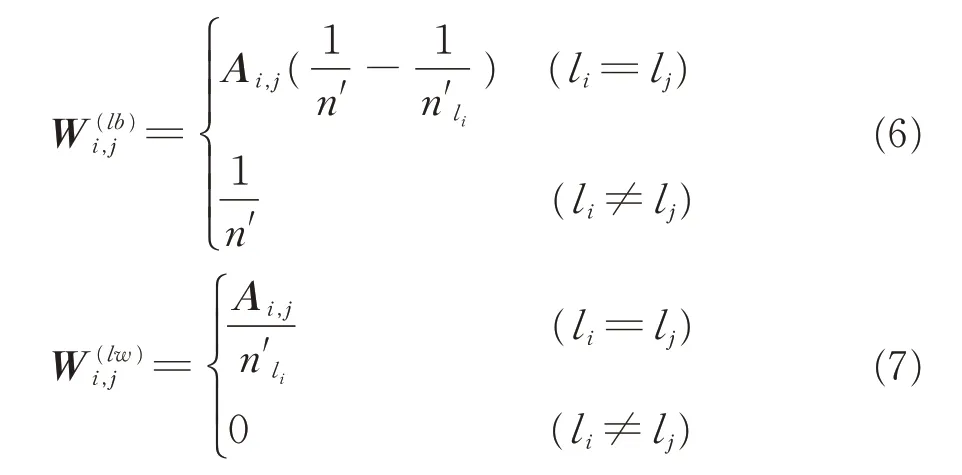
其中:n'li为 第li∈{1,2,…,c}(i=1,2,…,n')类 样本数;Ai,j∈[0,1]为相似矩阵。
Ai,j用于描述2 个样本点xi和xj之间的相似性。若两点间的相似程度越大,则Ai,j就越大,反之则Ai,j越小。Ai,j具有多种不同形式的定义,笔者采用局部尺度启发式的定义形式计算Ai,j
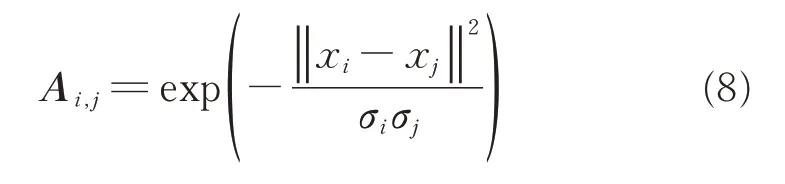
其中:σi为样本点xi的局部尺度,定义为σi=为xi的第k个最近邻点,设置超参数k=7[17]。
SELF 的目标函数定义为
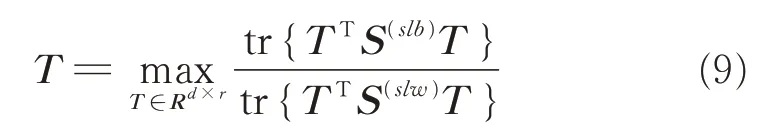
转换矩阵T的求解可以转化为如式(10)所示的广义特征向量求取
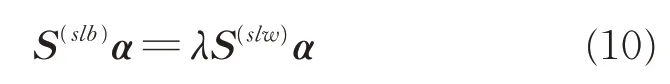
其中:λ为广义特征值。
选取前r个最大广义特征值对应的广义特征向量(α1,α2,…,αr)组成转换矩阵T。但是,SELF 本质上仍属于线性化的降维方法,在解决非线性数据时比较困难,为了进一步提高SELF 的性能,通过核方法,将SELF 的作用范围引入到非线性领域。笔者选用高斯核函数,将SELF 的应用推广到非线性领域。KSELF 定义的局部类间散度矩阵和局部类内散度矩阵分别为
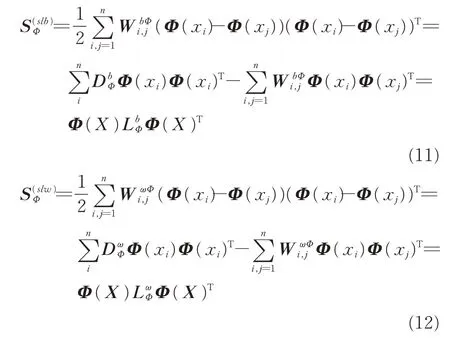
式(10)的广义特征值问题等效为
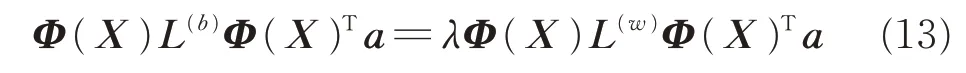
根据再生核理论可知,广义特征向量α可以表示 为a=Φ(X)φ。 在 式(13)两 边 同 时 左 乘Φ(X)T,得到
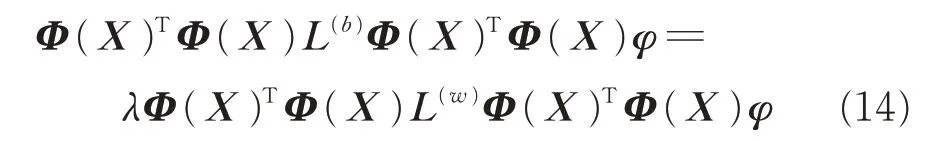
此时引入高斯核函数K(xi,xj)=ΦT(xi)Φ(xj),得到KSELF 的目标函数为
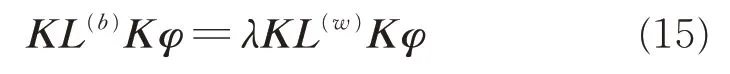
其中:φ为核样本向量
进而得到KSELF 的转换矩阵T,由式(15)的d个最大特征值λ1≥λ2≥…≥λd所对应的特征向量(φ1,φ2,…,φd)组成。
2.2 KSELF 算法具体实现步骤
输入高维数据样本集X={xi∈Rd}(i=1,2,…,n',…,n),包 含 类 别 标 签 样 本xi(i=1,2,…,n')和低维特征空间目标维数r。输出投影转换矩阵T和低维数据集Y。KSELF 算法具体实现步骤如下:
1)采集振动数据,从时域、频域和时频域方面提取特征指标,构建原始数据特征集并进行数据归一化处理,得到新的数据集X;
2)通过高斯核函数将X映射到高维特征空间H,得到Φ(X);
5)求解KL(b)Kφ=λKL(w)Kφ的广义特征值和特征向量,得到前d个最大特征值对应的特征向量(φ1,φ2,…,φd)组成投影矩阵T;
6)根据公式Y=TTΦ(X)计算高维数据集X所对应的d维数据集Y。
3 实验结果与分析
3.1 数据集
实验数据来自于如图1 所示的双跨度转子故障模拟实验台。设置实验台的采样频率为5 kHz,转速为2800 r/min,用12 个电涡流传感器分别采集该转子实验台轴系不对中、轴承松动、质量不平衡、动静碰磨和正常转动5 种状态的振动信号各80 组,选取其中的50 组作为训练样本(其中60%为有标签样本),剩余的30 组作为测试样本。从振动信号的时域、频域及时频域中提取故障特征参数,构造出12个通道的特征集合。各通道故障特征参数如表1 所示,共得到12×21=252 个特征,即252 维高维数据集。

图1 双跨转子实验台Fig.1 Double-span rotor test bench
3.2 实验结果分析
将高维故障特征集输入KSELF 进行训练学习与维数约简。为表现一般性,权系数采用折中取值,即β=0.5。根据文献[17],设定KSELF 中样本点邻域大小k=7,为充分涵盖原始数据集的本质信息,设定低维子空间的维数d=4(目标维数=故障类别数−1)。实验从以下方面来验证所提方法的有效性。
1)降维可视化对比。分别用PCA,KPCA,LFDA,KLFDA 和SELF 算法的降维效果和KSELF算法进行对比验证,得到的降维可视化结果对比如图2 所示。文中核参数选取采用五折交叉验证法选取最优核参数,得到KPCA,KLFDA 和KSELF 的核参数σ分别为75.6,62.5 和20.5。
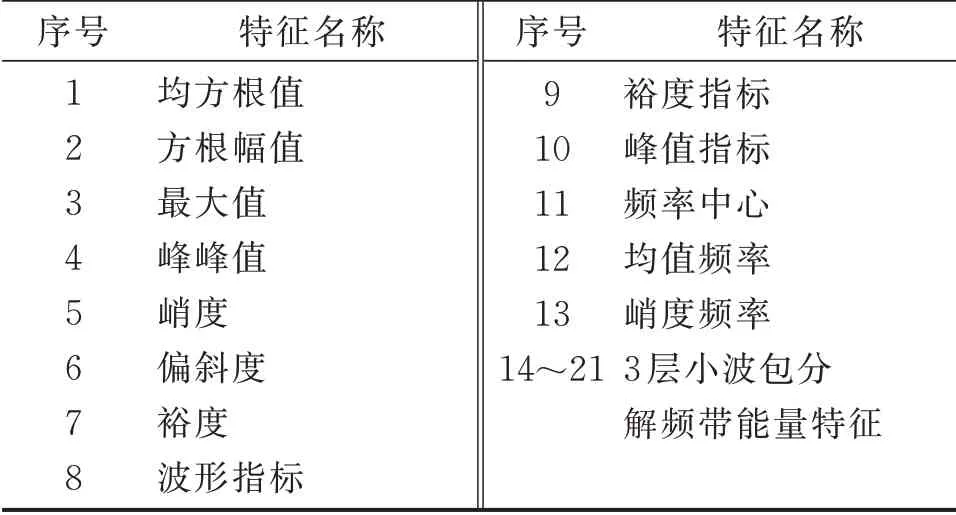
表1 各通道故障特征参数Tab.1 Fault characteristic parameters of each channel
从图2 可以看出,PCA 降维后的测试样本分类效果不理想,这是因为PCA 是基于二阶统计信息,其只能保持数据最大方差方向的投影,忽略了原始特征空间的非线性特征结构。KSELF 降维后的分类效果最好,各故障类内间距小、类间距离明显,这是因为其具有较强的非线性提取能力,并能有效地利用标签信息和无标签信息来提高故障识别率。其他4 种算法的分类效果介于二者之间。
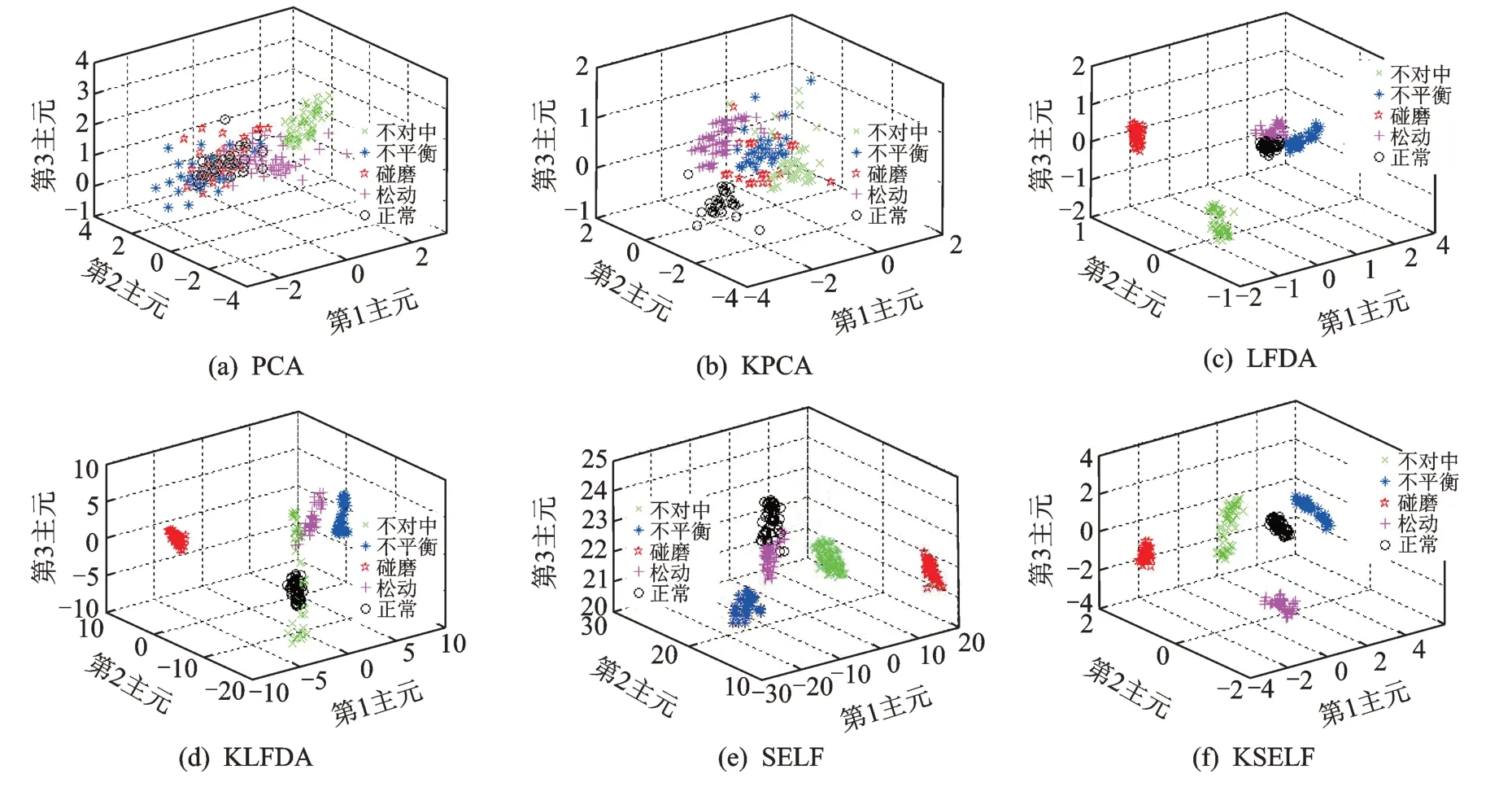
图2 测试样本基于不同降维方法的降维效果Fig.2 The results of test sample based on different methods of dimension reduction
2)故障诊断的本质是模式识别,为了直观有效地描述上述6 种方法的降维效果,将各降维方法的识别准确率如表2 所示。
从表2可以看出:①有监督的降维方法LFDA,KLFDA,SELF 和KSELF 降维后的识别准确率高于无监督降维方法PCA 和KPCA,这是由于监督降维方法能够通过类别标签信息,寻找具有判别能力的低维特征,无监督降维方法无法通过利用标签信息的指导作用进行维数约简,容易丢失大量有用的信息,使得整体的识别率较低;②半监督降维方法SELF 和KSELF 的 识 别 率 高 于PCA 和LFDA,这是 因 为SELF 和KSELF 继 承 了PCA 和LFDA 两 种算法的优势,能综合利用标记样本和无标记样本;③引入核方法的降维算法,利用核映射将特征集中的非线性问题转化成线性问题,能够有效去除空间中的噪声与冗余信息,得到更高的识别率。
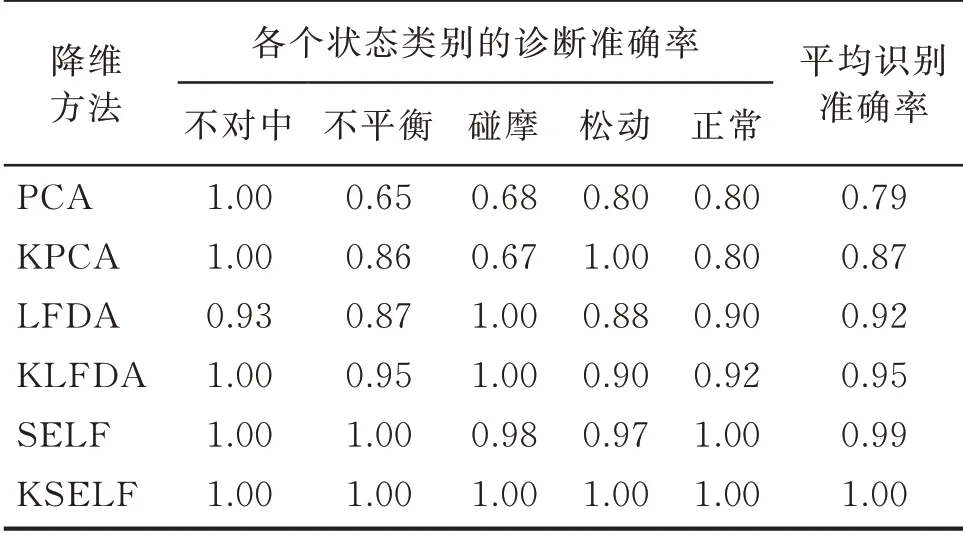
表2 各降维方法的识别准确率Tab.2 Methods of dimension reduction of recognition accuracy %
3)为了验证KSELF 方法在数据降维问题的优越性,选用不同的训练样本和测试样本比例(测试样本中60%为标记样本),将各降维方法降维后的低维 矢 量 输 入 到K 近 邻(K-nearest neighbor,简 称KNN)分类器中进行故障辨识,得出不同训练样本比例下的降维结果在KNN 中对应的平均识别准确率,如图3 所示。
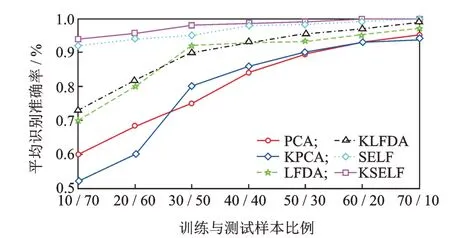
图3 不同训练样本比例对应的平均识别准确率Fig.3 The average recognition accuracy on the different number of training samples
从图3 可以看出:6 种降维方法降维后的识别准确率随着训练样本比例的增加而不断增大;PCA 和KPCA 的识别准确率在训练样本数较少的情况下下降明显,而其他监督降维方法的识别准确率整体上下降不明显;KSELF 一直很稳定,基本不受影响,表明提出的KSELF 算法是一种稳定且高效的降维方法。
为了进一步测试KSELF 方法中有标签样本与无标签样本的不同比例对降维效果的影响,随机设置训练样本中有标签样本个数分别为10,15,20,25,30,35 和40。经各降维算法训练降维后,将得到的低维测试样本输入KNN 分类器,得到平均识别率。不同标记样本数目与故障识别率的关系如图4所示。从图4 可以看出:①PCA 和KPCA 属于无监督的降维算法,不能利用有标签故障样本的信息,因而未受到不同标记样本个数的影响;②LFDA,KLFDA,SELF 和KSELF 降维方法随着训练样本中有类别标签样本个数的增加,其分类识别率也随之增加,这是因为随着故障标记样本个数的增加,可利用的先验信息变多,过拟合现象随之减少,故障识别率增加;③有监督的降维算法LFDA 因为过度依赖标记样本中的信息,受标记样本个数的影响较大,其识别率随着标记样本个数的增加变化明显;④半监督降维方法因能同时利用标记样本和无标记样本,在少量标记样本的情况下得到的识别率比较高,体现了半监督降维算法相比无监督和有监督降维方法的优越性。
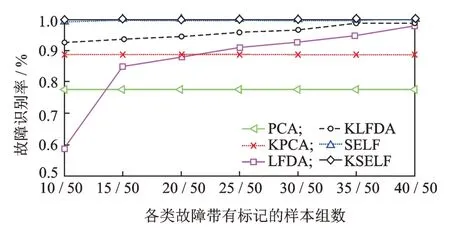
图4 不同标记样本数目与故障识别率的关系Fig.4 Relationship between the number of different labeled samples and the fault recognition rate
4 结束语
为了从复杂的高维和非线性故障数据集中提取有效的低维敏感特征子集,笔者从核方法和半监督角度出发,提出了一种基于核半监督局部Fisher 判别分析的方法。该方法具有有效利用有限数量的标记样本和一定数量的未标记样本来最大化识别的能力,通过核函数将原始数据特征集中的非线性问题转化为线性问题,可以很好地处理非线性的复杂故障数据。通过KSELF 降维,实现高维数据映射到低维数据,其类间数据间距离最大化和类内邻近数据间距离最小化。通过双跨度转子实验台故障模拟实验,验证了KSELF 方法优于其他算法,具有更高的故障识别精度以及更强的降维能力和泛化能力。该方法为复杂旋转机械故障诊断的智能化诊断提供了一种新思路。

