ARIMA模型在丙型肝炎月发病数预测中的应用

刘双，柳晓琳

(1.锦州医科大学公共卫生学院，辽宁 锦州 121000；2.辽宁省朝阳市第二医院，辽宁 朝阳 122000)

丙型病毒性肝炎(简称丙肝)，是由丙型病毒性肝炎病毒引起的一种传染性疾病，血液途径、性途径、母婴途径为其扩散的主要方式[1]。世界卫生组织在2017年的报告中估计，全球丙肝感染率为1.0%，约有7100万人为慢性丙肝感染病例，而中国2006年丙肝血清流行病学调查结果显示，丙肝感染率0.43%，由此推算，中国丙肝感染者约为560万。目前人群中尚没有有效预防接种的生物制品进行注射，丙肝的防治已成为严重的公共卫生问题[2]。基于统计分析和数学模型等方法对丙肝疫情发展规律进行预测，是丙肝疫情的控制、预防以及卫生决策过程中不可或缺的科学依据。ARIMA模型是最基本应用最广泛的模型之一[3]，它用相应的数学模型描述一组依赖于时间的随机变量相互之间所具有的自相关性，以表征预测对象发展的延续性并从时序的过去值与现在值预测其未来值[4]。

本研究运用ARIMA模型对朝阳市2009年1月至2020年12月丙肝月发病数进行时间序列发展趋势的研究，预测2021年朝阳市丙肝发病数，旨在为今后卫生行政部门传染病防治和卫生应急工作部署提供参考依据。

1 资料与方法

1.1 一般资料

根据“中国疾病预防控制信息系统”中的“传染病报告信息管理系统”，于2009年1月至2020年12月期间，收集朝阳市丙肝月发病数据。考虑到人口基数较大，最终本次研究以疾病的发病数代替了发病率进行分析预测。

1.2 方法

1.2.1 ARIMA建模步骤

应用SPSS 26.0软件中ARIMA模型进行数据处理与分析。ARIMA模型建模过程包括4个阶段：(1)数据平稳化处理：将2009年1月1日至2020年12月31日，丙肝月发病数的数据分为两部分：2009年1月1日至2019年12月31日，丙肝月发病数作为训练集构建时间序列模型，2018年1月1日至2018年12月31日，2020年1月1日至2020年12月31日，丙肝月发病数的数据作为验证集评价模型预测效能，绘制丙肝月发病数时序图判断序列的特征及平稳性，对非平稳的原始序列采用差分的方法以达到序列平稳化，采用单位根(ADF)检验验证序列平稳性；(2)模型的识别和定阶：根据平稳序列自相关系数图(ACF)、偏自相关系数图(PACF)进行初步识别和定阶，估计p、q、P、Q取值，在ARIMA模型中，P和Q的取值一般在0、1、2中选择[5]，通过不同的取值构建多个模型；(3)模型参数估计和模型诊断：采用非线性最小二乘法对模型的参数进行估计，对参数进行t检验，残差序列进行白噪声Ljung-Box检验，根据贝叶斯信息准则(BIC)最小为标准综合判定最优模型；(4)模型预测效果评价：采用平均绝对百分比误差(MAPE)和均方根误差(RMSE)[7-8]评价预测模型。平均绝对百分比误差主要用来反映真实值与预测值之间差异的大小，计算公式：∑[|实际值-预测值|×100 /实际值] /样本量。均方根误差通常用于比较真实值与预测值之间的误差，真实值和预测值之间的误差越大，均方根误差越大，计算方法：预测值与真实值差值的平方和与样本量的比值的平方根。

1.3 统计学方法

采用Excel 2007及SPSS 26.0软件对2009年1月至2020年12月的朝阳市丙肝月报告发病数进行录入及整理，建立ARIMA时间序列模型预测2021年1月至2021年12月朝阳市丙肝发病趋势。

2 结 果

2.1 数据平稳化处理

构建朝阳市2009年1月至2019年12月丙肝月发病数原始时间序列图并进行趋势分解，见表1、图1，显示该序列为非平稳时间序列，丙肝历年发病数呈现明显的上升趋势(χ2=187.780，P<0.001)并具有明显季节性效应，在2018年发病数达到峰值，之后稍作回落，每年的发病数在3月达到高峰。

对数据进行一阶差分以及一阶季节性差分，使序列基本平稳化，长期趋势及季节波动基本消除，见图2，采用单位根(ADF)平稳性检验P<0.001，证明序列处于平稳状态。

2.2 模型识别和定阶

根据原始时间序列特征分析，原始数据是以S=12为周期的季节性时间序列，经过一阶差分以及一阶季节性差分后，序列平稳化，可初步确定模型的参数d=D=1，因此初步确定模型的基本形式为：ARIMA(p，1，q)(P，1，Q)12，绘制数据预处理后平稳序列的ACF图和PACF图，时间序列的自相关系数在1阶之后趋于平稳，偏自相关系数在2阶之后趋于平稳，见图3～4。初步判定p=1和q=2。根据相关经验，p(P)与q(Q)取值超过2阶的情况很少，所以P、Q取为0，1，2进行筛选。考虑模型的拟合效果、最小信息准则和残差序列等有关指标综合进行评价。

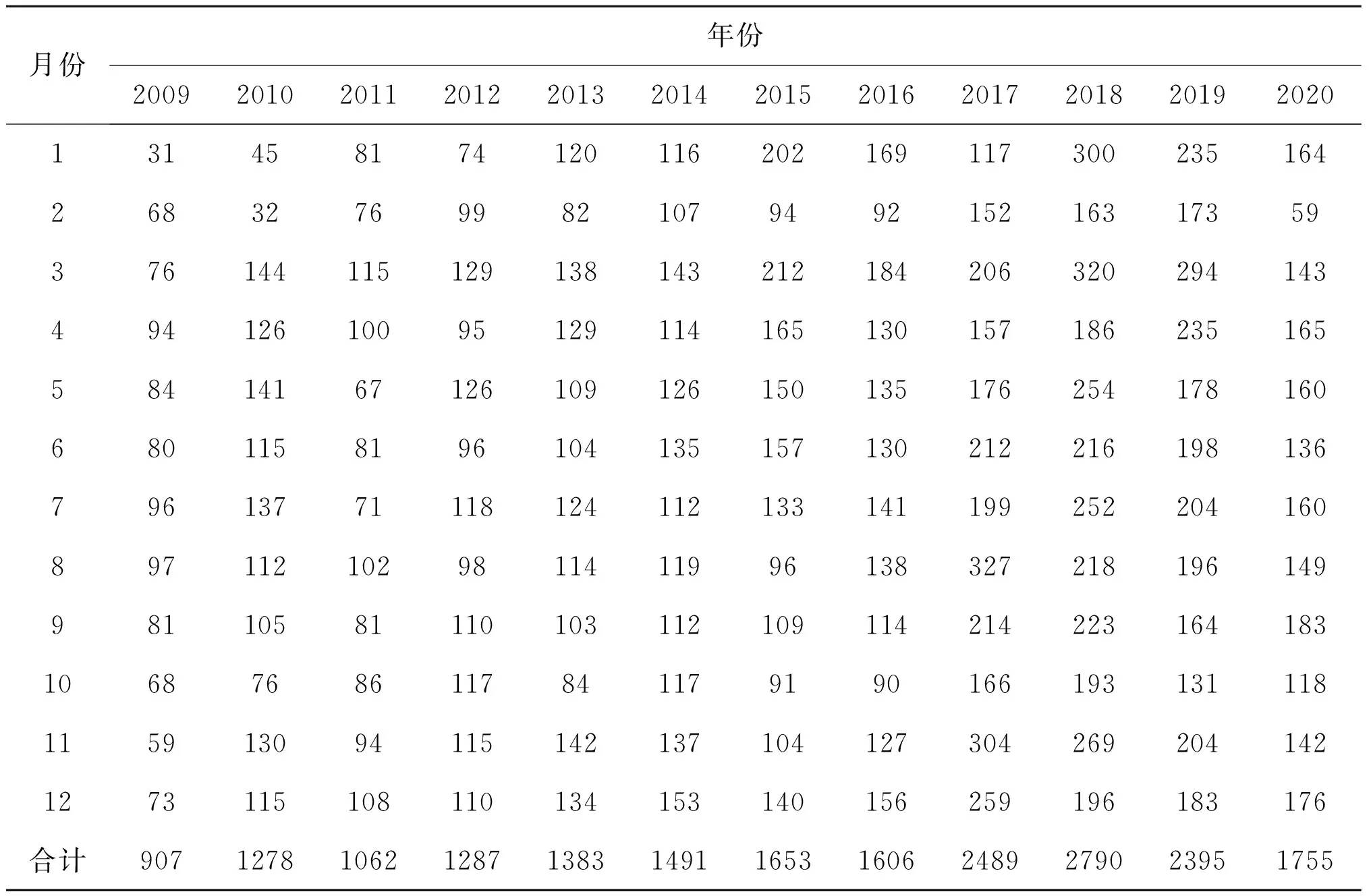
表1 2009—2020年朝阳市丙肝月发病数

图1 2009—2019年朝阳市丙肝月发病数原始时序图

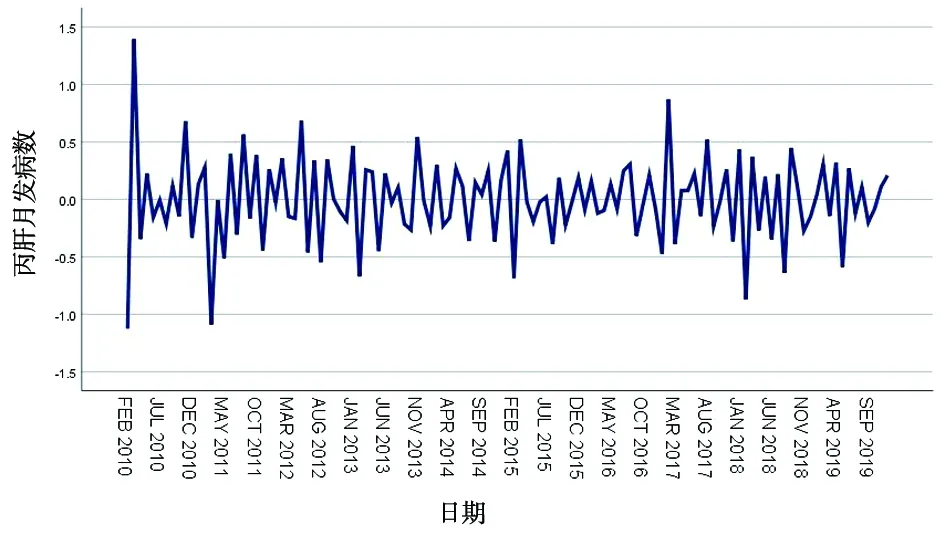
图2 2009—2019年朝阳市丙肝原始时间序列一阶差分及一阶季节性差分后平稳时序图

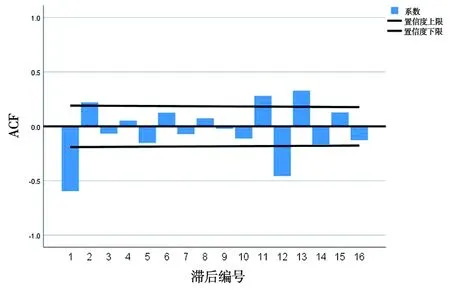
图3 丙肝月发病数预处理后的时间序列自相关图

2.3 模型参数估计和模型诊断

利用SPSS 26.0软件建立丙肝预测备选模型，通过白噪声Ljung-Box检验和模型系数的t检验要求，剔除不满足要求的模型，得到四个备选模型信息，见表2。根据BIC值最小原则选择最优模型，其中BIC最小模型为ARIMA(1，1，2)(1，1，2)12，并通过白噪声检验，P>0.05，可认为各个时滞的残差之间无相关性，残差序列为白噪声序列。对确定的最优模型的参数进行t检验，P<0.05，模型参数检验具有统计学意义；模型的拟合优度值平稳R2=0.656，认为模型拟合良好，BIC=7.350，结果最小，认为模型较优，见表3。

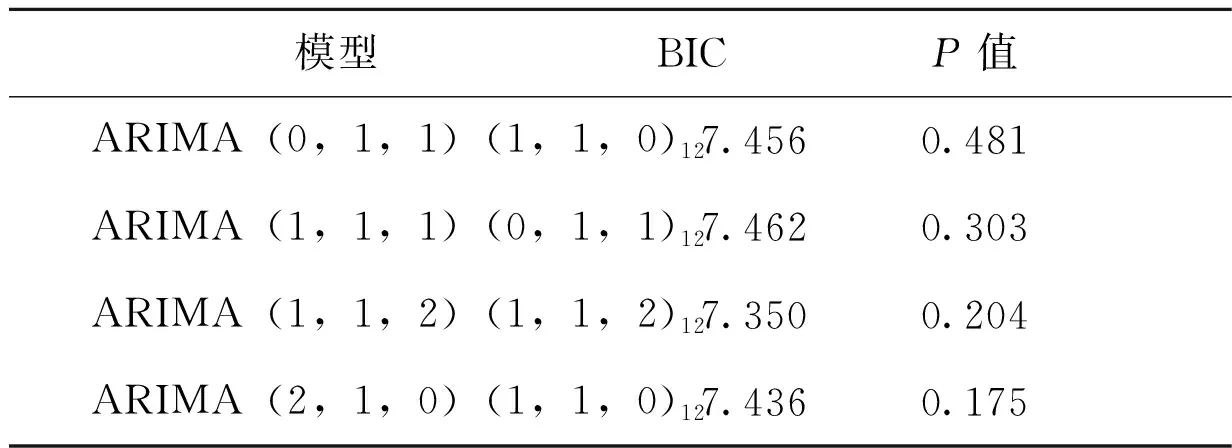
表2 丙肝备选模型信息表

表3 模型参数估计与检验结果情况

2.4 模型预测及效果评价

运用筛选出的最优模型ARIMA(1，1，2)(1，1，2)12对朝阳市2020年的数据进行拟合预测，采用MAPE及RMSE评价模型预测效能，根据预测值及真实值得MAPE=9.41%，RMSE=15.17，见表4、图5。再次运用2009年1月至2017年12月丙肝月发病数据对2018年丙肝的月发病数进行拟合预测，由真实值及预测值得MAPE=6.40%，RMSE=15.92，见表5、图5。运用朝阳市丙肝月发病数两次对最优模型的预测效果进行评价，MAPE<10%，RMSE<20，认为模型的精度较高，预测效果良好。

运用模型ARIMA(1，1，2)(1，1，2)12对2021年12个月的数据进行拟合预测，结果显示2021年朝阳市丙肝整体的发病数有所上升，合计发病1885例，较2020年丙肝发病数1775例上升了6.20%，预计在未来3月为丙肝的高发月，见表6。

图5 2009—2020年朝阳市丙肝月发病数模型拟合结果

表4 2020年朝阳市丙肝月发病数预测值与真实值比较

表5 2018年朝阳市丙肝月发病数预测值与真实值比较

表6 2021年朝阳市丙肝月发病数预测值

3 讨 论

ARIMA模型近年来被广泛应用于传染病的短期预测[9]，它不仅综合考虑了疾病可能存在的长期趋势、季节效应、周期性及随机波动，而且对模型的参数采用量化的方式进行检验并评价模型优劣，具有建模过程简单、经济、实用，短期预测精度高等特点[8]。丙型肝炎病毒多损害患者肝脏，因具有较强的传染性、较广的涉及范围、较高的发病率和较为复杂的传播方式，是我国常见的一种对人群威胁较大的血源及性传播传染病[9]。2019年新型冠状病毒肺炎疫情席卷全球，仍是当前和未来一段时间最为严重的“国际关注的公共卫生事件”和“重大危机”，故本文分别对2018年、2020年月发病数进行了回代性预测，得到丙肝最优模型ARIMA(1，1，2)(1，1，2)12，平均绝对百分比误差均小于10%，均方根误差均小于20[10]，显示ARIMA模型预测朝阳市丙型肝炎未来的走势及发病数，预测精度高，效果好。运用构建的最优模型对2021年12个月丙肝发病数进行预测，若2021年朝阳市疫情的发病情况属于正常范畴，则实际发病数应落在预测值95%置信区间内；若2021年朝阳市疫情的发病情况呈现暴发或流行趋势，则实际发病数处于预测值95%置信区间外，建议疾控机构及卫生管理部门快速响应，控制疫情蔓延。研究结果显示朝阳市2021年丙肝发病数呈上升趋势，延续了2009—2020年丙肝的发病走势，这与荆州市[11]、包头市[12]流行趋势相同，与各级医疗机构实验室检测技术的提高、疾病筛查敏感性的增强、各级疾控机构对传染病直报工作的督导有关。在未来3月发病数有所上升，考虑与2月是中国农历新年，就医量明显下降，3月新年过后，大量患者医院就医而导致病例增多。提示卫生管理部门应在3月加强对丙肝的防治及管理工作，做好宣传，提高大众防病、控病意识。

运用ARIMA模型进行丙肝预测应保证充足、完整的基础数据，一般要求具有30个以上的时间序列数据，7～8个以上的季节周期月发病率序列值。本研究数据包含了12年共144个月的发病数，满足ARIMA建模对数据的要求，这从一定程度上降低了ARIMA模型本身的局限性。因仅应用了“传染病报告信息管理系统”上报的监测数据而丙肝的流行状况往往受到经济水平、社会环境、政治因素、人口流动和生活方式等多种因素的影响[13]。当影响丙肝流行的因素发生重大变化时，如疫苗的普及，卫生条件的改善等，将导致预测值和实际值之间明显不符，故ARIMA只适合短期预测，不适合长期预测。需在实际应用中，不断加入新数据，对模型反复的识别及诊断，确定最优模型，今后可多维度分析丙肝发病趋势，提高预测的准确性，拟合出精度较高的模型[14]。

综上所述，ARIMA模型对朝阳市丙肝未来的流行趋势预测效果较好，这对了解朝阳市丙肝的流行病学特征、流行趋势、未来防治重点及制定相应的预防控制措施，防止丙肝的暴发及流行具有重要的公共卫生意义，可为丙肝的防治提供科学参考。