基于LSTM 的高铁大风预测模型及算法研究

李 隆，王 瑞，张惟皎

（1. 中国铁道科学研究院 研究生部，北京 100081；2. 中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081）

目前，我国已在高速铁路沿线全面布设了风速风向传感器，为高铁列车运行提供实时风速风向监测报警数据。高铁防灾系统具备了大风实时监测报警功能[1]，但尚不具备预警功能，灾害预警能力不足。如果系统能够通过当前时刻的风速数据，预测未来一段时间的风速值，进而对大风做出预警，就能让调度和工务人员提前做好应急处置准备，更好地保障高铁运营安全。

近年来，关于铁路大风预警的研究主要以铁路监测的大风数据为基础，采用时间序列等方法开展风速预测，相关学者已经做了大量工作。其中，刘辉等人开展了基于时间序列的非平稳ARIMA 预测模型、卡尔曼滤波、小波分析与神经网络结合等铁路风速预测方法[2-3]；王瑞等人[4-5]研究了基于RBF 神经网络的铁路沿线短时风速预测方法。铁路大风预警的方法还包括气象学模式、遥感预测模式、专家系统预测模式、时间序列解析预测模式、神经网络预测模式、时间序列与神经网络结合、气象模式与神经网络结合等[6-12]。以上研究中，基于ARIMA 和卡尔曼滤波的模型较简单，但预测结果精度一般；小波模型需要预先选择小波种类，且对非平稳数据的处理效果一般；RBF 神经网络秒级预测相对误差较小，分钟级以上的预测效果一般。

本文通过建立长短周期记忆（LSTM，Long Short Term Memory）[13]神经网络模型，利用其拥有长短期记忆的特点，增加风速预测的时间尺度，并通过数据分析、试验验证，建立在20 min、30 min 及1 h 的时间尺度下带有置信度计算的大风预警模型，可为大风灾害的应急处置工作提供参考。

1 高铁防灾中风速的采集

1.1 风速采集装置原理及参数

从安全、便于维护的角度，高铁防灾普遍采用非机械式的超声波风速风向仪（无桨叶或风杯）作为风速采集装置，与气象部门普遍采用的机械式传感器有所区别。声音在空气中的传播速度会与风向上的气流速度叠加，超声波风速风向仪利用超声波时差法，计算风速，采样频率为1 Hz，具体参数如表1 所示。

表1 超声波风速风向仪具体参数

1.2 风速采集装置的布设

高铁防灾系统中风速采集装置安装于铁路沿线，一般间隔5～10 km，现场安装如图1 所示。

图1 高铁沿线风速采集装置布设示意

风速采集装置面向田野侧，固定于铁路轨旁的接触网杆4 m 高处，采用双传感器冗余配置。传感器安装高度及位置有利于更准确的测量风对经过列车的影响。由于临近地表，风速风向受地形地貌影响较大，与高空风数据差异明显，无法直接采用气象部门的气象站数据作为参考。

2 预测模型及算法

2.1 LSTM 神经网络模型

风速的时序变化，既受短期内湍流因素的影响，又受到中长期温度、气压等因素的影响。LSTM 神经网络作为一种特殊的循环神经网络，其通过记忆存储单元的设计，能够有效避免梯度消失与爆炸。因此，本文基于LSTM 神经网络构建风速预测模型，能够较好地描述风速变化的长短期特征，从而对风速值进行更精准地预测。LSTM 神经网络结构如图2所示。

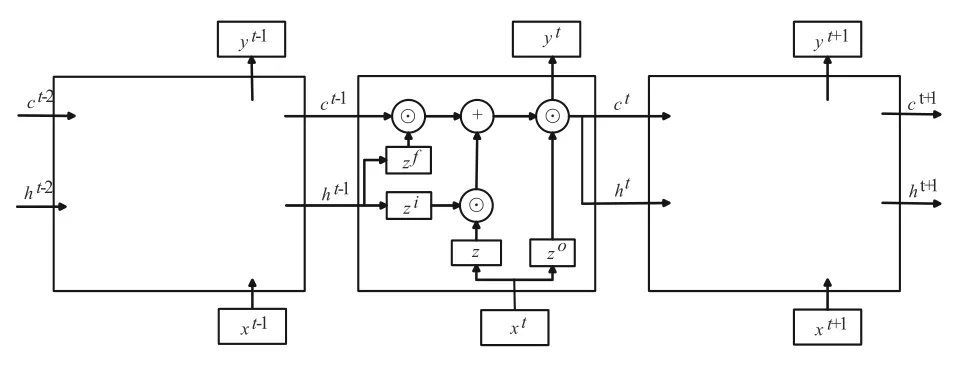
图2 LSTM 神经网络结构

其中，xt-1、xt、xt+1为输入的时间序列；c为变化较为缓慢的传输状态；h为变化较快的传输状态；yt-1、yt、yt+1为输出的预测时间序列；zf、zi、zo为遗忘门、输入门、输出门的门控状态，通过Sigmoid 函数将输入数据转换到（0，1）之间；z将对应时刻数据通过tanh 激活函数转换到（−1，1）之间。yt为t时刻归一化后的预测结果，可由W′同ct与ht组成的增广矩阵的乘积进行Sigmoid 激活求得，其中，W′为参数矩阵，其参数值将在训练中迭代更新。具体公式如下：

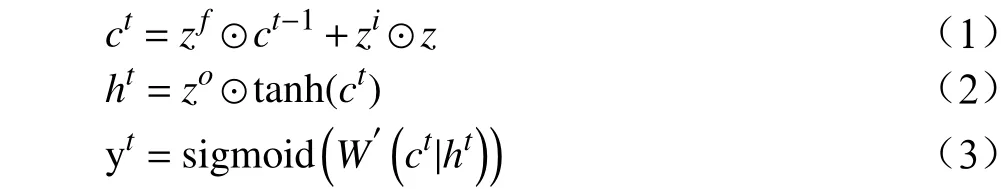
其中，⊙指将矩阵对应元素相乘的运算。

2.2 风速预测训练网络架构

本文采用1 层LSTM、1 层Dropout、1 层Dense全连接作为风速时间序列预测的网络架构。采用当前时刻之前的10 个20 min 平均风速记录作为输入序列x(xt-9,xt-8,···,xt)，预测未来20 min 的平均风速yt+1。（1）由于神经网络中模型参数较多，大风样本的数量有限，因此，直接使用风速数据训练LSTM 模型容易造成过拟合。虽然在训练模型训练集上，损失函数小，拟合效果较好，但在测试数据上损失较大，预测准确率下降；（2）Dropout 是深度网络中常见的一种正则化技巧，在训练网络结构中添加Dropout层，在每次训练的前向传播中以一定概率使部分神经元停止作用，增强模型的泛化能力；（3）使用Dense 层将多个神经元的结果作为输入进行加权和输出，从而计算出预测数据。

2.3 风速预测值置信度计算

将预测风速的误差视为高斯分布，其中，预测值作为期望，拟合标准差作为该高斯分布的标准差。设预警阈值为A，预测值为H，拟合标准差为σ，则预测风速为x时，置信度φ计算公式如下：

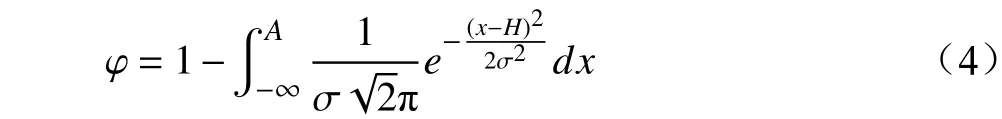
3 数据分析

3.1 计算方法

本文选取了有代表性的某高速铁路客运专线某日包含大风报警在内的12 h 风速数据。按1 h、30 min、20 min 时间尺度分组，计算整段时间平均风速，以及序列t时刻对应时间尺度的平均风速Xt，进而计算自相关系数、偏自相关系数。

k阶自相关系数Rk计算公式：

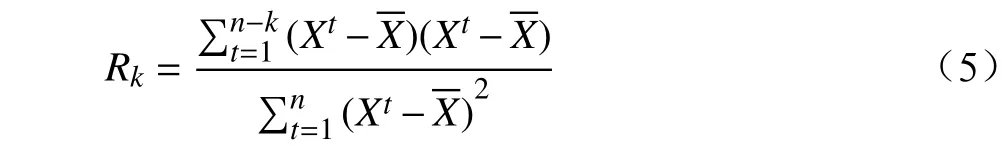
k阶偏自相关系数ρk计算公式：

3.2 分析结果

使用Python 进行计算，并调用Matplotlib 可视化分析结果。如图3～图5 可知，各组不同时间尺度的平均风速在12 h 内为非平稳数据，自相关系数及偏自相关系数均为拖尾。由一阶自相关系数可知，20 min 时间尺度平均风速的自相关性较强，30 min时间尺度平均风速的自相关性中等，1 h 时间尺度平均风速的自相关性较弱。平均风速的时间间隔越长，相关性越小。因此，利用历史平均风速预测未来平均风速的方法时，采用20 min 的时间尺度效果较好，否则将出现较大偏差。

图3 1 h 时间尺度平均风速数据分析

图4 30 min 时间尺度平均风速数据分析

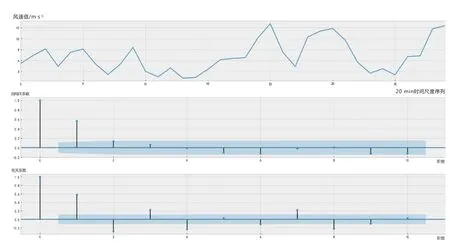
图5 20 min 时间尺度平均风速数据分析

4 试验验证

4.1 试验数据及分组

本文采用某高铁客运专线铁路防灾系统大风时段416 400 s 的历史数据作为样本，样本数据特征如表2所示。

对每20 min 的样本数据求平均值，共得到347个数据，作为时间序列。取前200个作为训练数据集，后100个作为测试数据集，剩余数据做为验证数据集。将均方误差（MSE，Mean Square Error）作为代价函数的输出误差。

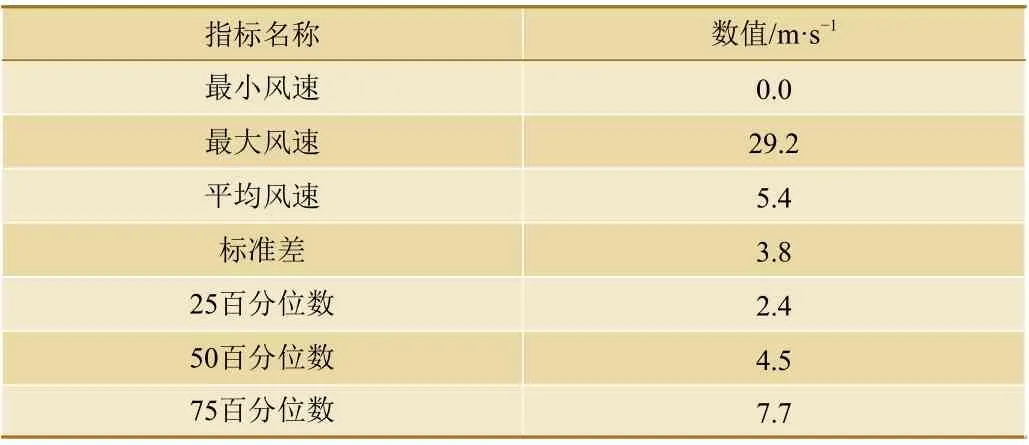
表2 样本数据特征

4.2 模型训练及结果验证

本文使用TensorFlow 搭建预测模型，并将分组数据导入，进行模型训练及结果验证。试验结果如图6所示，纵坐标为风速值，横坐标为20m in 间隔的时间序列；蓝色曲线为每20m in 的平均风速序列，绿色曲线为训练数据集，黄色为测试结果，红色为验证数据集结果。

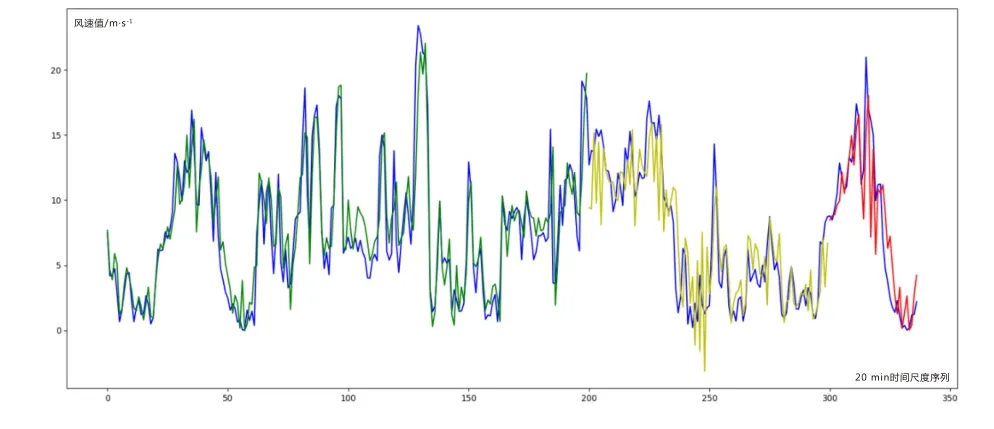
图6 风速预测结果

本次测试验证集MSE 为16.65(m/s)2。多次实验结果显示：在20～30 m/s风速值下，测试集MSE在15～20(m/s)2之间，拟合标准差在3.87～4.47 m/s，风速预测平均误差13.4%。如选取大风预警的阈值为15m/s，拟合标准差采用4.2 m/s，当未来20 m in 的平均风速预测为16 m/s时，大风预警的置信度可根据公式（4）计算得φ ≈0.77，在预测风速的同时，提供了大风预警的置信度，使预测结果更具参考价值。

5 结束语

本文介绍了现有高铁防灾系统中风速数据的采集方法，基于历史大风数据进行统计分析，建立LSTM 模型来预测未来短时间内风速平均值，并提供预警置信度。能较好地预测未来20m in 平均风速趋势变化，并且在大风速情况下依然保持较高的准确度，预测20～30 m/s大风时平均误差为13.4%。本研究旨在充分利用现有高铁防灾系统数据基础上，提供大风预测并提高预测模型精度。为更加精准地做好大风灾害的预报工作，仍需考虑与气象大数据相结合，进行多模式融合分析。