自旋转变材料中压强调制的自旋泵浦

宿凤琴，焦虎军

（山西大学 物理电子工程学院，山西 太原 030006）

0 引言

在自旋转变材料中，通过调节温度、光照、压强等外界条件会导致系统在高自旋态与低自旋态之间转变，这种自旋转变现象由于其物理重要性和潜在的应用价值受到了人们的广泛关注［1-4］。典型的例子如［Fe（trz）3］（BF4）2呈现的记忆效应已经用作自旋电子器件的开关元件［5-6］。自旋转变现象主要出现在含铁、钴、镍、锰离子(3dn，4≤n≤7)的磁性系统中。以Co离子为例，在压强诱致的自旋转变研究中，Vankó等人最早采用X射线发射谱在LaCoO3中发现压强可以调节钴离子的自旋态转变［7］。之后，Lengsdorf等人在金属铁磁单晶La0.82Sr0.18CoO3中也发现随着压强的增加钴离子发生了高低自旋态转变并伴随着系统发生金属绝缘体转变［8］。此外，Jia 等人［9］在 BiCoO3中，Kim 等人［10］在CoCl2中及Yang 等人［11］在SrCoO3中都发现了压强诱致的高低自旋态转变现象。近来，Liu等人在PbCoO3中发现随着压强的增加，二价钴离子从高自旋态转变为低自旋态；降压后又从低自旋态恢复到高自旋态［12］。自旋泵浦作为产生纯自旋流的一种重要方法，它指的是在铁磁共振的作用下自旋流从铁磁材料中被泵浦到邻近的顺磁金属材料中［13-14］。目前，人们已经在磁性金属［15-16］、半导体［17-19］、绝缘体［20］中实现了自旋泵浦，对于一些二维系统，如石墨烯［21-22］、过渡金属硫化物［23］、自旋玻璃材料［14］中也观测到了自旋泵浦。由自旋泵浦产生的自旋流的探测可由顺磁金属中的逆自旋霍尔效应来实现，即将自旋流转化为可测量的横向电荷流或电压差［24-26］。近来，实验已经实现了在ITO/YIG中的自旋泵浦所导致的逆自旋霍尔效应的观测［27］。我们已经开展了自旋转变材料中的温度调制的自旋泵浦效应研究［28］，但其压强对于自旋转变材料中自旋泵浦流的影响还没有开展，本文以自旋转变材料|顺磁金属双层膜系统为研究对象，通过调制外加压强，引起自旋转变材料的自旋态发生转变，进而导致注入顺磁金属中的自旋流及产生的电压呈现压滞现象。

1 理论模型与方法

在一些过渡金属离子化合物中，当过渡金属离子的外层电子为d4-d7时，由于电子配对能E和晶体场Δ的互相竞争，金属离子可能呈现高自旋（HS：high-spin）基态或低自旋（LS：low-spin）基态。通过改变压强等外界条件可调节两种态之间的能量差，当其与kBT（kB：玻尔兹曼常数，T：温度）处于同一量级时，进而使过渡金属离子发生高低自旋态的互变，即自旋转变现象。以Co3+（d6）为例，5个简并的d轨道在晶体场作用下会分裂为两组，在弱晶体场中，即Δ＜E，d电子的分布构型为，高自旋态（HS）稳定，自旋量子数S＝2；通过增加压强，可使晶体场分裂能增大，当Δ＞E，即进入强晶体场时，d电子的分布构型变为，低自旋态（LS）稳定，自旋量子数S＝0（如图1）。

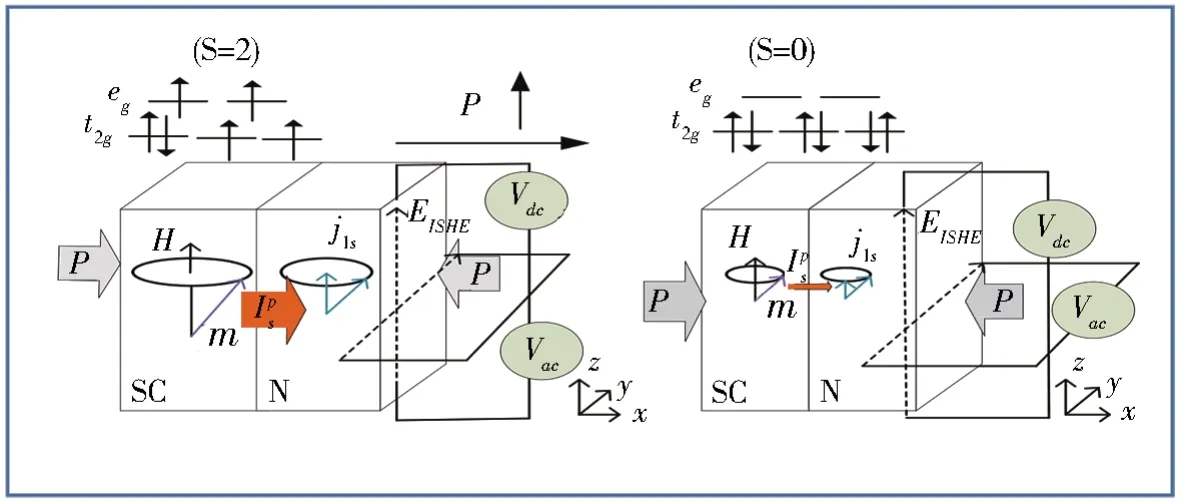
图1 压力下自旋转变材料（SC）与顺磁金属（N）构成的双层膜系统，自旋转变材料的高低自旋态，磁化进动及注入自旋流示意图，其中P为外加压强，H为外加磁场，m为磁化单位矢量，为自旋转变材料泵浦进入顺磁金属中的自旋流，j1s为顺磁金属中的自旋流密度Fig.1Schematics of a spin-crossover material（SC）|normal metal（N）bilayer，the high-spin state and the low-spin state in the spin-transition material，the magnetization precessions and the injected spin currents under pressure.P，H，m，，andj1sstand for the external pressure，the applied magnetic field，unit vector of the magnetization direction，the spin current from spin-crossover material pumped into the normal metal，and the spin current density in the normal metal，respectively

在实验上已经发现，压强可以使自旋转变材料的自旋态发生相互转化［12］。对于这类材料系统，我们采用Bolvin等人的理论描述方法［29］，对于离子间自旋相互作用采用平均场近似，我们可将系统的摩尔自由能表示为

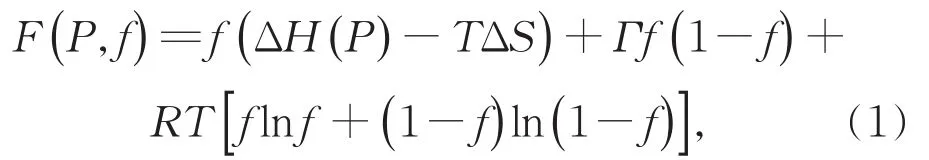
上式中，ΔH(P)表示高低自旋态转变时系统的摩尔焓变、ΔS为系统的摩尔熵变，f为高自旋态粒子的摩尔分数。这里我们引入了与分子间相互作用相关的焓为Γ，R为气体摩尔常数，P为压强，T代表绝对温度。压强能够对焓变、熵变及分子间相互作用焓项都产生影响，但最重要的是焓变部分，只保留对焓变贡献，在最低阶近似下，可认为其随压强线性变化［30］，即ΔH(P)＝aP—b，这里a、b都是常数。给定压强下，高自旋态粒子的摩尔分数可由平衡时自由能极小值给出，即须满足dF(P，f)/df＝0，d2F(P，f)/df2＞0。这样可得高自旋态粒子的摩尔分数f(P)满足下式：

由于高自旋态离子间的自旋相互作用，铁磁性自旋转变材料的磁化强度大小可以表示为M＝NgμBSf，这里g是朗德因子，μB是玻尔磁子，N是单位体积内的过渡金属离子数。

对于铁磁性的自旋转变材料，在外加磁场H、交变场hrf的共同作用下，其动力学过程由Landau-Lifshitz-Gilbert方程给出［25］：

这里，γF、αF分别代表自旋转变材料的旋磁比和Gilbert耗散常数，m给出磁化方向的单位矢量。有效场Heff是由外磁场H、交变场hrf及由材料形状决定的退磁场Hd共同确定，即Heff＝H+hrf+Hd，在这里，对于面内存在磁场的薄膜，Hd＝—(M·ex)ex。对于铁磁自旋转变材料与顺磁金属（如Pt）构成的双层膜系统，由于有效场的驱动，双层膜界面处会形成非平衡的自旋累积，当交变激发频率达到共振条件（M是磁化强度大小）时，泵浦进入顺磁金属中的自旋流可写为［25-26，31］

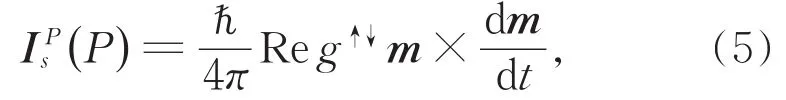
式中g↑↓为无量纲自旋混合电导，它取决于界面通道数及界面处顺磁金属不同通道间的反射系数，其主要由顺磁金属的性质决定［32］。实验和理论都表明 Reg↑↓＞＞Img↑↓［33-34］，后面的计算中我们只保留了实部的贡献。由于压强能够有效改变自旋转变材料的磁化强度，这样就能有效改变铁磁共振频率，进而影响磁化进动角度，从而改变注入顺磁金属中的自旋流大小。目前可以把双层膜系统放入金刚石对顶砧装置上实现加压实验，压强的常用精确标定方式通过红宝石荧光线的位移来确定，目前的精度可达到 0.1 GPa［35-36］。

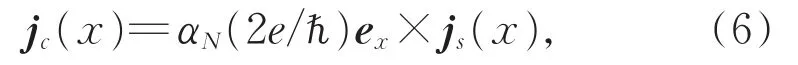
这里αN为金属的自旋霍尔角，在平衡状态下，我们可以得到其对应的交流电场和直流电场分别为

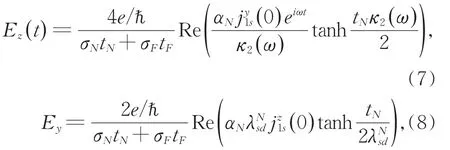
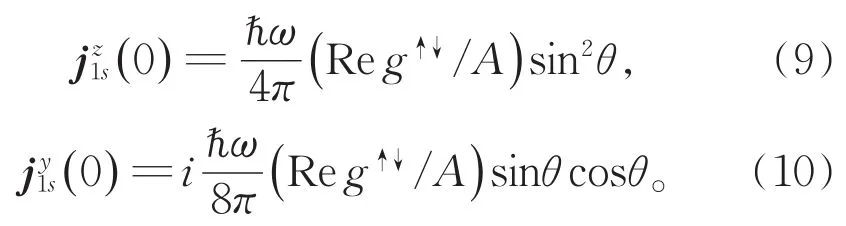
这样我们就可以分别得到直流电压和交流电压分别为V＝EyL、V(t)＝Ez(t)L，这里L表示顺磁金属薄膜的长度和宽度。

2 数值结果与分析

我们以自旋转变材料|顺磁金属Pt双层膜系统为研究对象，首先确定压强对于高自旋态粒子摩尔分数的影响。接着计算了在固定铁磁共振激发频率下，逆自旋霍尔效应产生的直流与交流电压大小随外加压强的变化情况。最后考虑了在不同自旋转变材料的导电性能以及不同正常金属厚度下直流与交流电压大小随外加压强的变化情况。我们选择的计算参数如表1所示。这里，我们选取界面混合电导实部为Reg↑↓/A＝3.6×1019/m2，记材料的厚度为t。

表1 自旋转变材料与顺磁金属Pt中的参数值［39-41］Table 1 Parameters chosen in spin transition material and Pt

首先我们计算了压强对于自旋转变材料中高自旋态粒子摩尔分数的影响。在通常的自旋转变材料中，高自旋态的摩尔焓变对压强的依赖可近似线性化表示为ΔH(P)＝aP—b，压强对于摩尔焓变的影响可以达到2 000cm—1·mol—1·GPa—1～3 000 cm—1·mol—1·GPa—1［30］，摩尔熵变ΔS～0～10 cm—1·K—1·mol—1范围内，计算中我们选取a＝2053.84 cm—1·mol—1·GPa—1，b＝66 563.34 cm—1·mol—1［30］。下面我们计算了不同分子间相互作用参数下摩尔分数随压强的依赖性（如图2a）。从图中可以看到，在分子间相互作用参数（如400cm—1）较小时，系统随压强的增大逐渐从高自旋态转变为低自旋态，转变过程没有突变；当降低压强时系统又从低自旋态回到了高自旋态，而且转变过程与增压过程完全重复，没有压滞回线的存在。当增大分子间相互作用参数（如600、800、1000cm—1）时，系统随压强的增大（或者减小）从高（低）自旋态转变为低（高）自旋态的转变是突变的，而且升压和降压过程中发生突变的压强也不同，这样完成一个循环就出现了压滞回线。把从高（低）自旋态突变为低（高）自旋态的压强记为Pup(down)，接下来我们计算了发生突变的压强Pup(down)随着分子间相互作用参数的变化情况（如图2b）。从图2b我们可以看到，只有当分子间相互作用参数达到一定值时，材料的高低自旋态转变才会出现压滞行为。当分子间相互作用参数小于此临界值时，系统虽然也发生高低自旋态转变，但转变过程是渐进的；而一旦超过此临界值，升压和降压过程的转变点就不再相同。进一步发现，随着分子间相互作用参数的增大，压滞回线的宽度（Pup—Pdown）也在增大。关于压滞回线存在的原因，我们认为分子间相互作用参数在一定范围内，整个系统自由能作为压强的函数存在两个极值，极值中对应能量较小的为稳定态，对应能量较大的为亚稳态。在低压下，系统呈现高自旋态，此时只有一个能量极小值点，对应于稳定态。随着压强的增加，高自旋态和低自旋态都成为能量极小值点，但高自旋态仍为稳定态；而低自旋态为亚稳态。

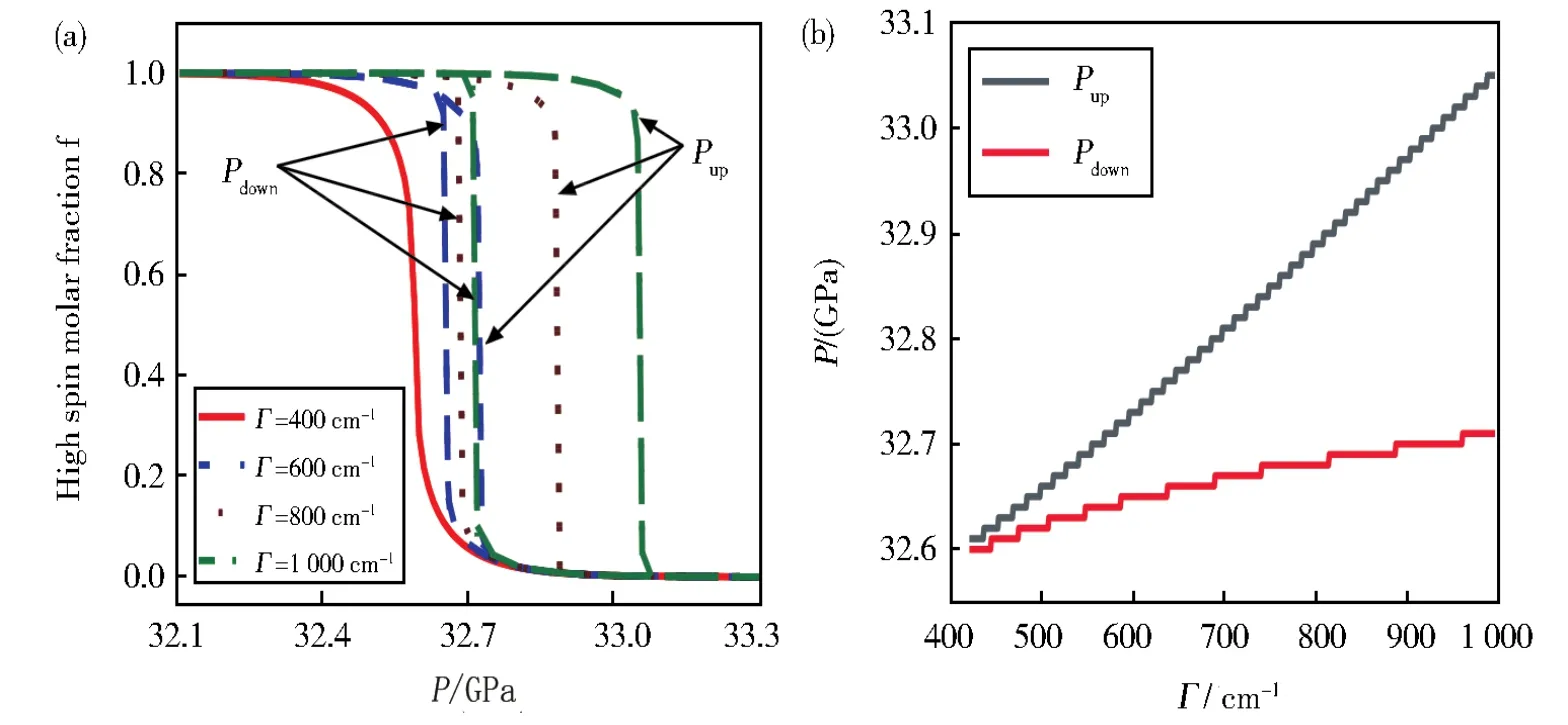
图2 高自旋态粒子的摩尔分数f随压强P的变化（a）和高低自旋态转变压强随分子间相互作用Γ的变化（b）Fig.2 Dependences of high-spin molar fractionfon pressureP（a）and the transition pressuresPupandPdownon the intermolecular interaction parameterΓ（b）

随着压强的进一步增加，高自旋态转变为能量较大的亚稳态，而低自旋态变为能量较小的稳定态，但是由于记忆效应，随着压强增加，系统仍保持在高自旋态；只有当压强继续升高，达到突变点时，系统才从高自旋态转变为低自旋态。反过来，当系统从高压开始降低压强时，系统一开始处于能量较小的低自旋态，随着压强的降低，低自旋态会从能量较低的稳定态转化为能量较高但仍是局域极小值的亚稳态，随着压强进一步降低，亚稳态消失，此时系统从低自旋态突变为高自旋态，因而系统随着压强的升降会呈现压滞回线。

进一步考虑自旋转变材料|顺磁金属Pt所形成的双层膜系统，当铁磁自旋转变材料发生铁磁共振时，会注入顺磁金属Pt中自旋流。实验中交变磁场的激发频率是固定的，通常是通过调节外磁场大小来改变自旋流，当外磁场大小正好满足共振条件时，注入的自旋流最大，而当外磁场发生偏离时，注入的自旋流将会衰减。这里我们固定激发频率，并调节外磁场正好满足共振条件，改变外加压强，研究可测量电压或电流随压强的变化情况，为了简化，我们这里忽略了外加压强对于材料厚度及材料导电性能的影响。首先考虑在不同分子间相互作用参数下，由于压强的改变，注入顺磁金属中的自旋流由于逆自旋霍尔效应所导致的直流电压（如图3a）和交流电压（如图3b）。由图可知，当分子间相互作用参数较小时，直流和交流电压随压强的变化不存在压滞回线；当我们增大分子间相互作用参数时，我们发现直流电压与交流电压均随压强的变化表现出了压滞回线。这是由于在较小的分子间相互作用参数下，压强较低时系统处于高自旋态，系统的磁化是由高自旋态粒子的摩尔分数决定的，此时系统正好处于共振条件，因而铁磁共振的锥角达到最大，这样注入的直流和交流自旋流就最大，从而测量到的直流和交流电压也最大；随着压强的增加，系统状态逐渐从高自旋态转变为低自旋态，因而系统的磁化逐渐减小，这样系统磁化的变化会逐渐导致系统偏离共振，共振锥角减小，从而注入的直流和交流自旋流会迅速下降，因而测量到的直流和交流电压也快速减小；同时在直流和交流电压中也不存在压滞回线。

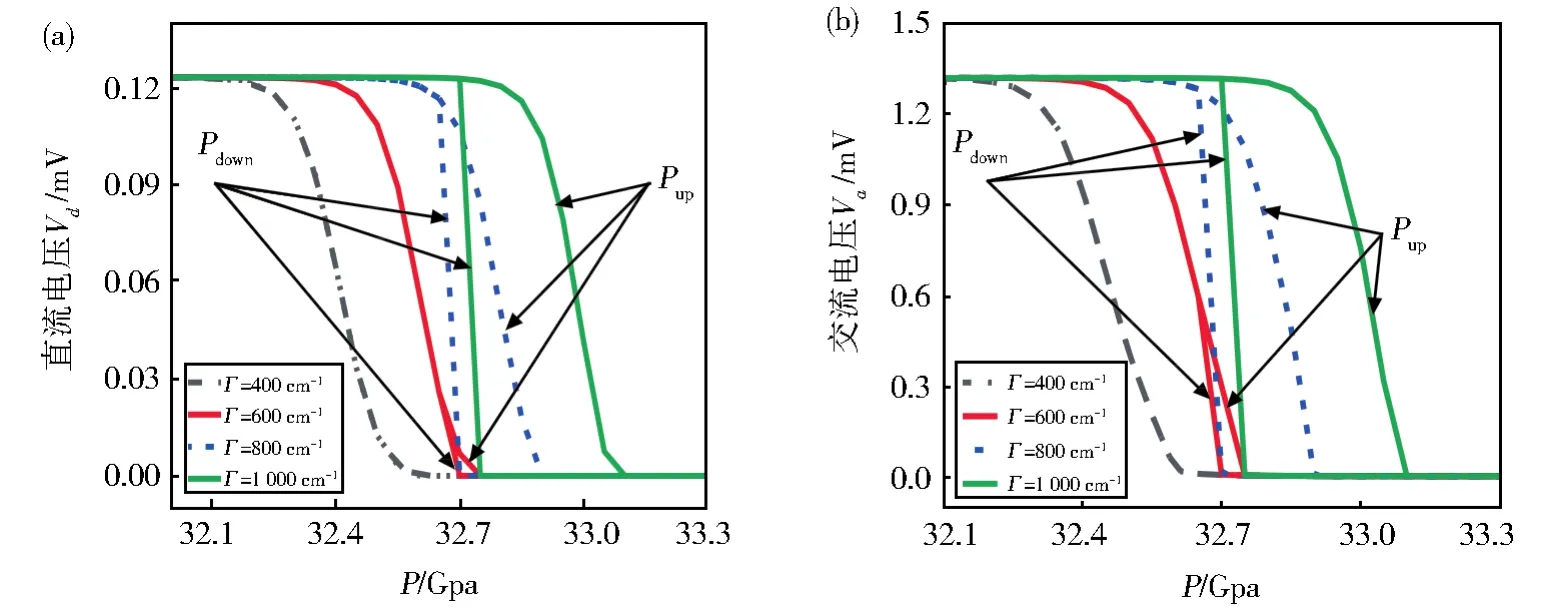
图3 直流电压Vd（a）和交流电压Va（b）随压强升降的变化Fig.3 Dependence of the DC voltage（a）and the magnitude of the AC voltage（b）on the increase and decrease of pressure；

当分子间相互作用参数较大时，随着压强的增加，系统状态从自由能单一极值的能量最低的高自旋态逐渐转变为自由能呈现双极值的高低自旋态，初始系统的高自旋态为能量低的稳定态，低自旋态为能量高的亚稳态，随着压强增加，高自旋态变为亚稳态，而低自旋态成为稳定态，但整个系统仍呈现为能量较高的高自旋态，这样系统的磁化及铁磁进动的锥角都较大，进而泵浦注入顺磁金属中的直流和交流都较大，这样通过逆自旋霍尔效应所转化的电流以及可测量的直流和交流电压都较大；随着压强进一步增大，高自旋态不再是能量极小值态，系统会从高自旋态突变为低自旋态，这时系统磁化大小会发生突变，因而进动锥角会急剧减小，这样泵浦的直流和交流自旋流会急剧衰减降低，从而可测量的直流和交流电压也就急剧减小。

反之，当降低压强时，系统状态变化从自由能单一极值的能量最低的低自旋态逐渐变为自由能呈现双极值的高低自旋态，初始时低自旋态为能量最低的稳定态，高自旋态为能量较高的亚稳态，随压强减小，低自旋态变为亚稳态，而高自旋态成为稳定态，由于记忆效应，系统仍表现为低自旋态，因而系统磁化一直较小，铁磁进动的锥角很小，因而注入的直流和交流自旋流及由逆自旋霍尔效应所导致的直流和交流电压都很小。随着压强进一步降低，低自旋态不再是能量极小值态，系统会从低自旋态突变为高自旋态，这时系统磁化大小会发生突变，因而进动锥角会急剧增加，这样泵浦的直流和交流自旋流及由此产生的直流和交流电压也就急剧增大，从而整个系统就呈现了压滞回线。

最后固定激发场频率f＝2.5GHz，以及固定发生共振的外场大小，选取分子间相互作用参数Γ＝800cm—1，在不同的自旋转变材料导电性能及顺磁金属厚度情况下研究了直流和交流电压大小随压强的变化情况（如图4）。其中图a与图c中对应绝缘体σF＝0Ω—1·m—1的情况；而图b 与图d中对应导体σF＝2×106Ω—1·m—1的情况。由图可以看出在不同的自旋转变材料导电性能或不同的顺磁金属厚度情况下，整个系统都呈现了压滞行为，它主要由分子间相互作用参数来决定，只要分子间相互作用参数足够大，且其压强效应不明显时，压滞行为就必然存在。进一步通过对比不同厚度的顺磁金属，我们发现随着厚度的增加，直流和交流电压大小都在减小。直流和交流电压大小与顺磁金属厚度的关系取决于两方面的效应，一个是影响注入自旋流的大小，另一个是导体的导电性能。因为我们选用的顺磁金属Pt的自旋扩散长度1.5 nm较小，对于注入自旋流大小的影响较小，主要是厚度较大时，电导增大，这样就会导致可测量的直流电压和交流电压大小减小。此外比较图中直流与交流电压大小（图4a与4c或者图4b与4d），很明显直流电压远小于交流电压的大小，这主要是由于注入的交流自旋流与共振时进动角的一次方成正比，而直流自旋流与进动角的二次方成正比，而进动角即使在共振条件满足时也是非常小的，因而交流电压大小远大于直流电压大小。

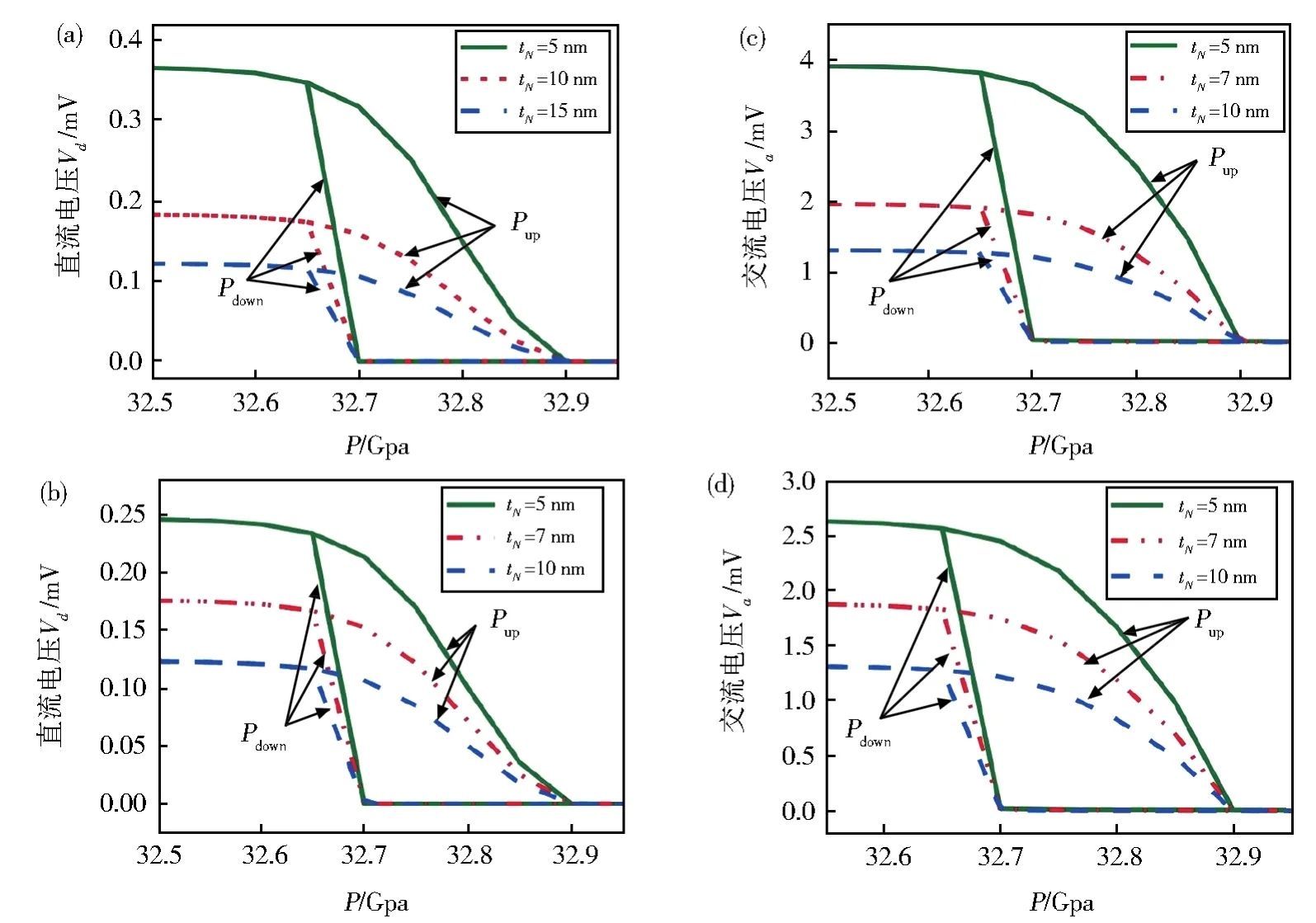
图4 不同自旋转变材料导电性能和正常金属厚度下，直流电压Vd（a）和（b）和交流电压Va（c）和（d）随压强的变化Fig.4 Dependence of the DC voltage（panels a and b）and the magnitude of the AC voltage（panels c and d）on the increase and decrease of pressure for different electrical conductivities in the spin-transition material and different thicknesses in the normal metal

进一步对比自旋转变材料是导体和绝缘体情况，我们可以看到在相同条件下，自旋转变材料是绝缘体时，直流和交流电压较大，这主要是由于当自旋转变材料为导体时，会提高整个系统的电导，因而降低可测量的电压大小。如果考虑压强对材料厚度及电导率的影响，虽然会影响具体直流电压和交流电压的数值，但自旋泵浦流及可测量的电流或电压中出现的压滞现象仍然存在。尽管压强标定精度可以达到0.1 GPa，但是目前高压实验仍然没有办法对特高压强进行精确调控，这正是观测自旋流压滞现象需要解决的关键实验问题。此外，如果能够有效调控分子间相互作用强度进而使压滞宽度增宽可能是解决自旋流压滞现象的一个有效方法。

3 结论

本文以自旋转变材料|顺磁金属Pt为研究对象，研究了外加压强对自旋泵浦的影响。在固定交变场激发频率和外加磁场条件下，发现随着外加压强的升降，泵浦注入顺磁金属中的自旋流存在压滞现象。我们发现随压强的增加，高自旋态占据的摩尔分数降低，使系统从高自旋态转变为低自旋态，在足够大的分子间相互作用参数下，高自旋态摩尔分数随压强的增加和减小呈现压滞回线。进一步计算了压强对泵浦进入顺磁金属中自旋流及由此产生的直流和交流电压大小的影响，发现压强较低时铁磁共振导致注入自旋流最大，进而产生的直流和交流电压达到最大，而随着压强增加，偏离铁磁共振时，泵浦自旋流所导致的直流和交流电压大小迅速衰减。并且在升压和降压过程中，自旋流和可测量的交直流电压大小都存在滞后效应，出现了压滞自旋泵浦现象。