微振荡并联双量子点AB干涉仪的量子输运特性

李林，李志坚

（山西大学 理论物理研究所，山西 太原 030006）

0 引言

量子点的电子输运是人们长期以来研究的课题，然而相关的研究工作很少考虑量子点与电极耦合界面的变化。实际上，量子点和电极界面很容易受到化学反应、局部热效应等的影响而产生结构性的变化。电子输运特性可能会对这种界面变化非常敏感，有时会提升输运能力，有时却会降低输运能力。界面变化的细节不可控制，界面的动力学行为对系统输运性质会产生何种影响值得进一步探究［1—4］。

近年来，随着实验上用微波或光辐射控制系统电子特性的操作越来越精密，人们对含时量子系统的输运性质的研究给予了更多关注［5］，包括发展新的输运理论来处理含时输运问题，使得量子输运理论更加完善［6—8］。量子点与电极耦合时，会有分子键的伸缩振动，形成依赖于时间的动力学系统。该理论考虑了系统的动力学效应，基于非平衡格林函数方法并遵循近似求解Dyson方程的原理，借鉴布兰德斯的想法把Wigner空间中表示的Kadanoff-Baym方程按质心时间的导数梯度展开［9—10］，最后给出系统电流的近似表达式。一些研究工作［11—13］使用了这种梯度展开的方法，探究了量子点与电极间耦合化学键的相应弹簧常数值以及化学键间的相互作用等对系统输运性质产生的影响。然而，在量子输运过程中，量子相干性起着非常重要的作用，会导致量子共振现象，使得电子输运特性发生很大的改变。量子系统与电极接触的界面变化产生的影响会如何改变相干量子输运特性，对于设计量子器件和改善其效能非常重要。并联双量子点体系是研究量子相干的典型模型，通过改变施加的磁通，系统的电导会展现出Fano共振、Kondo效应等量子相干特征。本文中，我们基于格林函数输运理论，考虑量子点和电极耦合界面在其平衡位置附近的振荡，以并联双量子点AB环为模型研究磁通的大小和量子点间耦合强度的变化对体系输运性质的影响。

1 理论模型

我们考虑由两个量子点组成的并联双量子点耦合到正常金属电极上，两量子点间存在隧穿耦合，并施加两个不同的磁通ϕL和ϕR，形成双AB环结构，如图1所示。系统的总哈密顿量由双量子点哈密顿量HM、左右电极哈密顿量HL和HR、左右电极和量子点的耦合哈密顿量HLM和HRM组成，可表示为

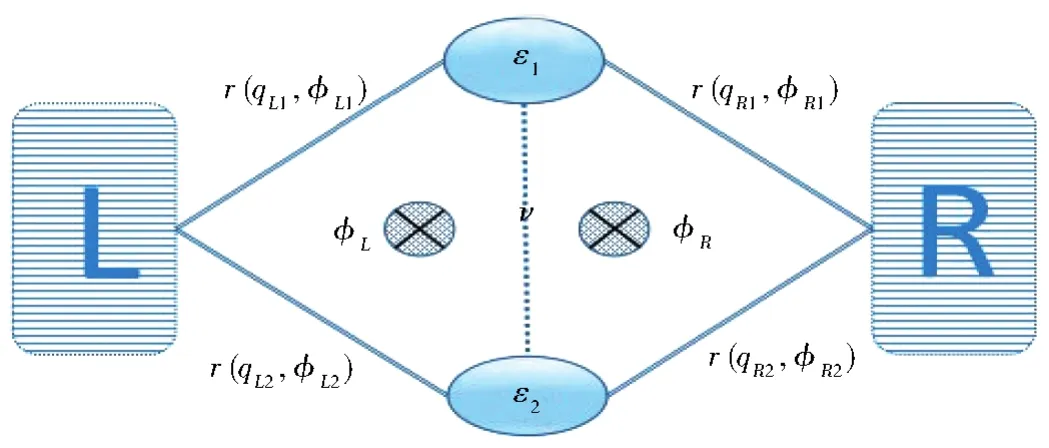
图1 与电极耦合的并联双量子点体系的结构示意图Fig.1 Schematic diagram of the double quantum dot coupled with the electrodes

左右正常金属电极可看作是无相互作用的费米海，其哈密顿量为

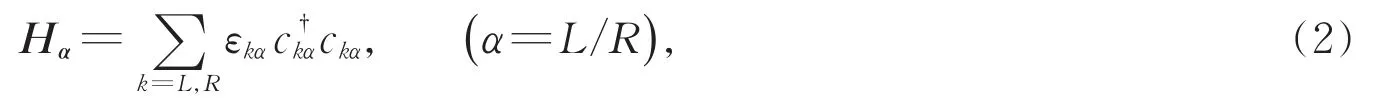
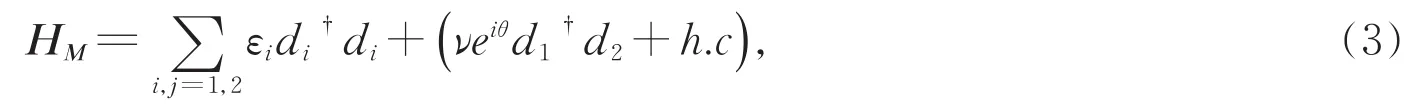
其中di†(di)表示第i(i＝1，2)个量子点中能量为εi的电子的产生（湮灭）算符，ν表示两个量子点间的耦合强度，θ＝2π(ϕL—ϕR)/ϕ0（ϕ0＝hc/e是磁通量子单位）表示电子从一个量子点隧穿到另一个量子点时相位的改变量。并联双量子点AB环与左右电极间的耦合哈密顿量HαM为

其中r(qαi，φαi)是量子点i与金属电极α的耦合强度，看作量子点i与电极α界面在平衡位置附近振荡位移qαi和电子通过该界面时相位变化φαi的函数。本文中我们选取，其中φ＝2π(ϕL+ϕR)/ϕ0是由两个 AB环的磁通之和导致的相位变化。假设耦合强度r(qαi，φαi)与振荡位移qαi和相位φαi有如下关系：

2 Wigner空间中电流的近似计算

2.1 Wigner空间中的电流表达式

2.2 Wigner空间中Kadanoff—Baym方程的近似解及电流的动态修正

3 结果与讨论

3.1 耦合参数λ对系统电导的影响

为了探究界面振荡对电流的影响，我们考虑系统处于平衡构型，即q→0时的情况，这里需要注意的是，虽然q＝0，但≠0。假设γL＝γR，则ΓL＝ΓR，从方程（22）式可知，这里零阶电导表达式与不考虑界面振荡时的电导形式一致，本文主要的工作是研究二阶电导的修正效应。

在不考虑磁通ϕα的情况下，取费米能级ω＝0，且ε1＝ε2＝ε时，系统的线性电导为

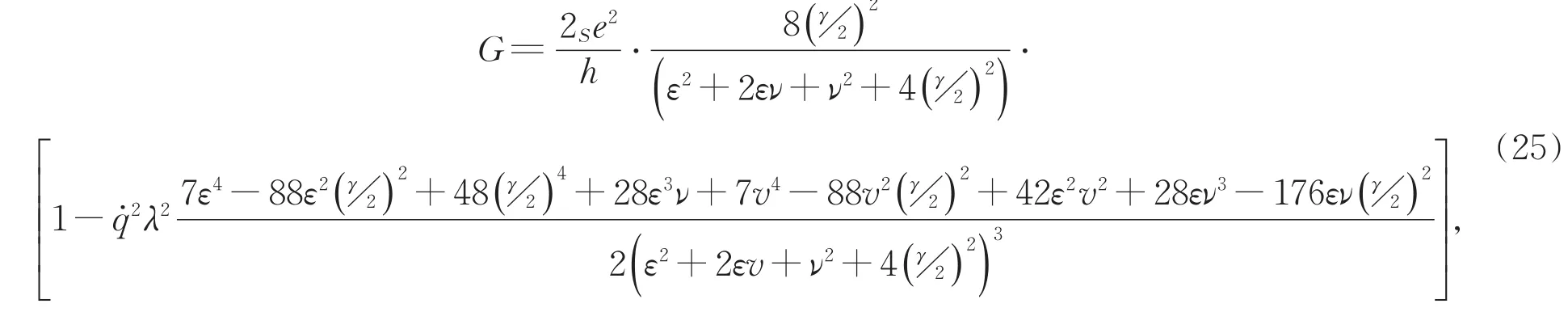
其中γ＝γL+γR。式中的第一项为零阶电导，正好是不考虑界面振荡时的电导表达式，第二项是与成正比的二阶修正电导。选取，把γ作为能量单位。图2是点间耦合分别在ν＝0和ν＝1的两种情况下，且耦合参数λ均为0、0.1、0.2、0.7、1、2时，电导随量子点能级的变化曲线。从图2（a）中可以看出，当λ＝0时，也就是没有考虑界面振荡时，电导的极大值为2，此时两个量子点的能级和费米面一致，两个量子点分别作为一条输运通道，系统同时能够输运两个电子。随着λ的增加，ε＝0处的电导值会由电导曲线的极大值变为极小值，转变点约为λ＝0.7。当ε＝0处出现电导极小值时，我们称为强耦合，否则称为弱耦合。不同λ值下的电导曲线总是相交于处，也就是此时电导的二阶修正项为零。当时，界面振荡总是会减小电导值，且耦合参数λ越大，降低的幅度越大。当时，界面振荡导致的二阶修正项则会增大电导值。随着量子点能级继续远离费米能级，又会导致电导减小，但减小的幅度较小。图2（b）给出当ν＝1时，电导随量子点能级的变化。与图2（a）相比，可以看出两个量子点间的耦合只会使得电导曲线向左平移ν，并不影响量子点的输运特性。类似前面的运算过程，可以得到单量子点系统的线性电导。图3给出单量子点系统和并联非耦合双量子点系统的电导比较，从图中可以看出，并联非耦合双量子点系统的零阶电导的峰值是单量子点系统的2倍，但二阶修正电导的峰值却是1/2倍。相对而言，并联双量子点系统会比单量子点系统受到界面的影响更小。通过改变耦合参数λ的取值大小，发现结果与上面讨论的情况一致，即与耦合参数λ的大小无关。

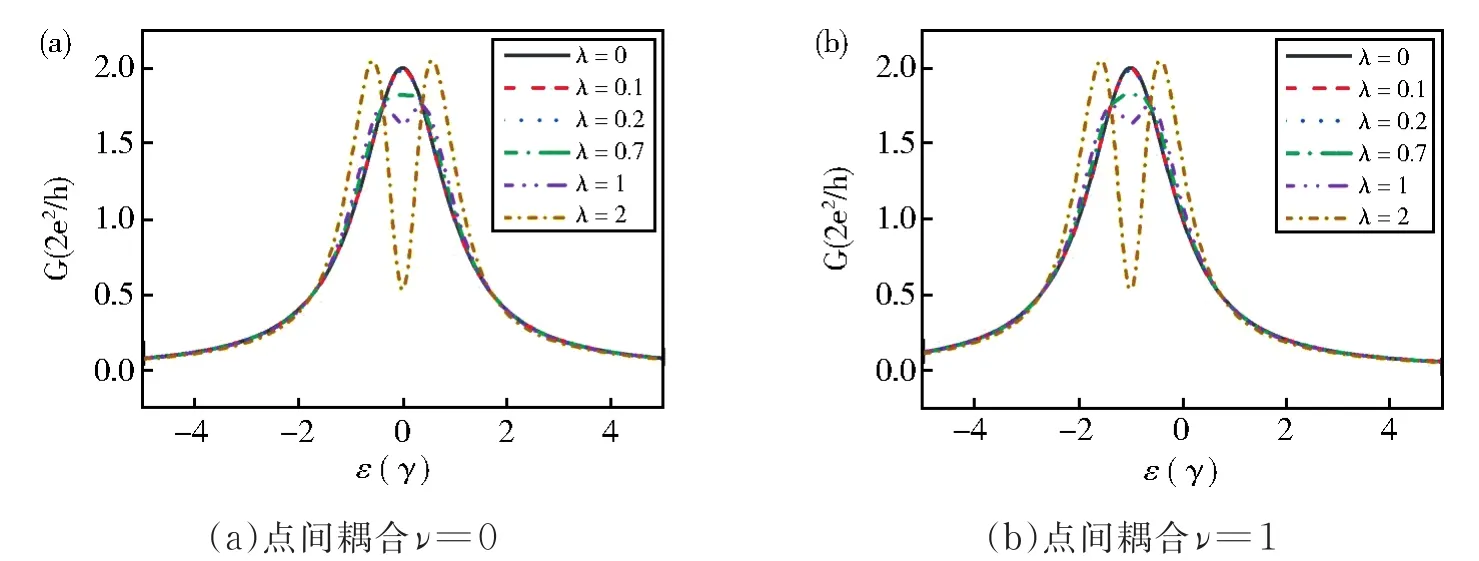
图2 不同耦合参数λ下电导随量子点能级ε的变化曲线，其余参数选取为，θ＝0，φ＝0Fig.2 Conductance as energy levelεof quantum dots under different coupling parametersλ.Parameters used in calculations are，θ＝0，φ＝0

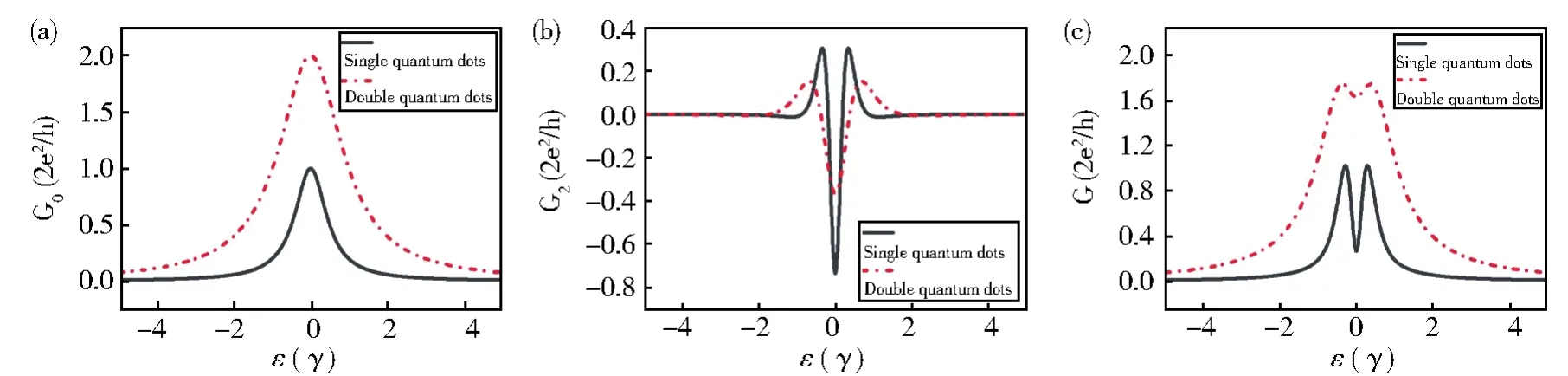
图3 （a）零阶电导、（b）二阶修正电导、（c）电导在单量子和并联双量子点两种系统中，随量子点能级ε变化的曲线对比图。参数选取实线 λ＝ 0.5，虚线 λ＝ 1，，v＝0，θ＝0，φ＝0Fig.3 Comparison of the curves of zero-order conductance（a），second-order modified conductance（b），and conductance（c）in single quantum and parallel double quantum dot systems with changes in quantum dot energy levelsε.Parameters used in calculations are λ＝ 1，，ν＝0，θ＝0，φ＝0

3.2 磁通ϕα对系统电导的影响

接下来我们研究并联双量子点AB环中磁通对电导的影响。前文中我们限定了通过两个AB环的磁通大小相等方向相反，所以φ＝0，只看两个相反方向的磁通差产生相位θ的影响。选取、λ＝0.2和ν＝1，在不同θ下电导随量子点能级的变化如图4所示。当θ＝0时，两个子AB环中的磁通都为零，结果和图2相同，只是由于选取ν＝1导致了电导向左平移（黑线所示）。当θ＝π时，ν前的相位因子eiθ等于—1，相当于ν反号，使得电导曲线（紫线所示）向右平移。在两种情况下，二阶电导修正很小。当θ＝π/2时，图4（a）中的零阶电导在ε＝±ν处出现完全对称的两个峰（蓝线所示），二阶修正电导同样关于ε＝0对称。当θ＝π/3时，零阶电导在ε＝±ν处虽然出现两个峰，但是两峰不对称，右侧峰形成了一个Fano峰（红线所示）。二阶电导表现出明显的不对称性，进一步增强了右侧峰的Fano共振行为。当θ＝2π/3时，观测到的左右峰的现象与θ＝π/3的情况恰恰相反，即Fano峰会出现在左侧（绿线所示）。由此可以看出，在弱耦合情况下，当θ≠nπ/2时，电导会出现Fano效应，二阶修正电导会因两个AB环中的磁通差的不同而改变，增强Fano共振行为。

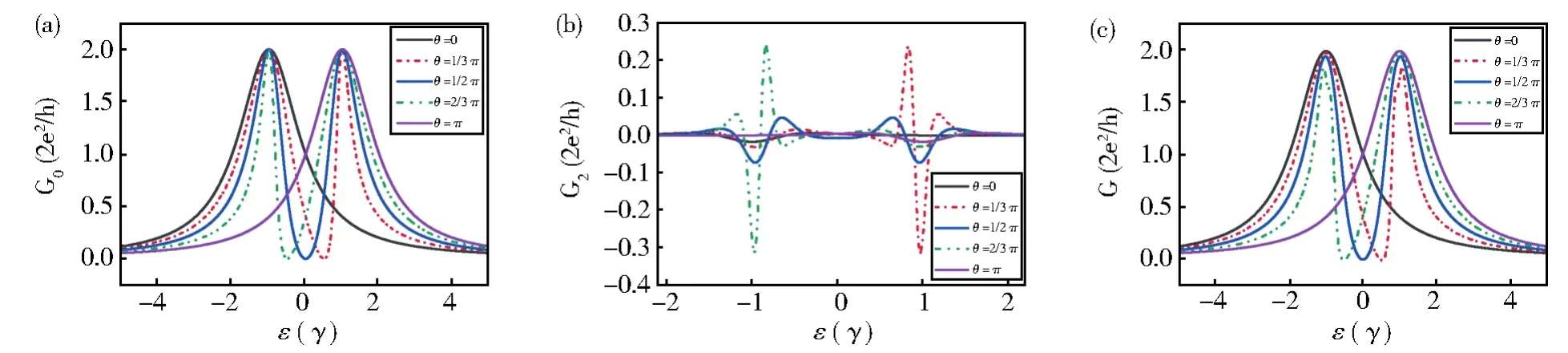
图4 磁通不同时，（a）零阶电导、（b）二阶修正电导、（c）电导随量子点能级ε的变化图Fig.4 Zero-order conductance（a），second-order modified conductance（b）conductance（c）with the energy levelεof quantum dots under different magnetic flux conditions

4 结论

我们采用非平衡格林函数方法，考虑量子点和电极之间的含时耦合效应，研究了并联双量子点AB环的输运特征。研究发现并联双量子点系统中量子点与电极耦合界面的振荡运动会导致系统的输运性能改变。在弱耦合情况下，发现通过改变AB两个子环之间的磁通量的大小，零阶电导会有Fano效应出现，二阶修正电导对该效应可以进一步增强，进而改变系统的输运性能。