基于无人机巡检技术的光伏电站缺陷精确定位及降重方法研究

姬学海，彭文博，高虎，李晓磊，朱纹哲

1.华能宁夏能源有限公司新能源分公司

2.中国华能集团清洁能源技术研究院有限公司

无人机用于光伏电站巡检，能极大提高巡检效率，降低巡检成本，正逐渐取代人工巡检。但是，现有巡检系统存在定位精度不高、重复定位等问题，导致巡检系统无法为工作人员提供完全正确的消缺依据，不能实现有效的光伏电站维护。因此，本文提出一种基于空中三角测量与缺陷去重处理相结合的缺陷坐标转换方法，降低了缺陷从图像坐标向地理坐标转换的误差，同时结合缺陷类型及计算出的地理位置进行缺陷降重处理，解决了因交叠拍摄造成的缺陷重复问题。本文选取装机容量为30MW的光伏电站进行测试，实验结果表明，本文所述方法既提高了缺陷定位精度，保证了缺陷的低重复度，能够为工作人员提供一种更为准确和有效的消缺依据。

随着我国能源网络战略的高效快速实施，以光伏发电为主的可再生能源供应能力不断增强。然而，光伏电站的运行和维护压力却在逐渐增大，因此无人机对光伏电站进行自主巡检是现实需求。无人机自主巡检的关键技术是，利用无人机导航和机器视觉技术，实现光伏设备航拍影像的自动化处理与分析，以及辅助定位。但是，现有无人机视觉巡检方案存在定位精度较低，容易造成不同角度拍摄的同一缺陷被重复定位等问题。同时，光伏电站消缺和维护过程会受地形、电站分布、电站覆盖面积等诸多因素影响。因此，如果无人机巡检系统缺陷定位不准确，会引发维护成本的增加。

为提升无人机巡检系统缺陷定位的可靠性和稳定性，首先须要考虑无人机航线规划及航拍方式，并保证准确地提取无人机拍摄位置及位姿等详细信息；其次为保证缺陷在原始拍摄图像上的准确度，采用高精度深度学习检测模型对图像上的缺陷进行检测。在作业过程中，无人机搭载红外及可见光等相机，采集多源传感器图像，同时采用配准技术进行图像配准，得到缺陷点在两种图像之间的对应关系；最后利用空中三角测量方法，测算每张图像实际拍摄位置的欧拉角，最终利用图像坐标、相机坐标、世界坐标之间的转换关系，得到缺陷点在地理位置上的坐标，利用得到的电站具体组件地理位置即可完成电站维护。

目前，无人机光伏电站巡检已经得到广泛应用。文献一详细介绍了光伏组件无人机巡检策略，以及在松湖渔光互补光伏电站的实际应用；文献二结合四旋翼无人机的具体飞控方式,对无人机飞行路径进行建模,使用粒子群算法得到最优贝塞尔曲线，作为无人机的飞行航迹,并通过实验验证了该方法的有效性；文献三探讨了无人机光伏电站巡检的飞行和巡检要求。此段省略了所提及的三个文献名称。

本文以实现精确定位和缺陷降重为主要目的，提出一种基于空中三角测量技术及去重处理技术相结合的缺陷坐标转换方法，降低了缺陷从图像坐标向地理坐标转换的误差，同时结合缺陷类型及计算出的地理位置进行缺陷降重处理，解决了因交叠拍摄造成的缺陷重复问题。实验结果表明，本文所述方法能有效提高缺陷定位的精度，同时减少因不同角度拍摄带来的缺陷重复定位。

数据采集

无人机根据预先规划的航线进行巡检，在数据采集过程中，无人机采用定点悬停的方式，使用双光相机同时采集红外图像和广角图像。为在巡检过程中不漏检光伏组件，无人机在相邻两次悬停位置处采集的图像存在交叠，同时交叠范围不宜较大，避免给以后运算或处理过程带来额外的工作量，具体交叠量可以根据实际需要进行选择，采集到的红外及广角图像位置对应关系如图1所示，虚线部分表示无人机在第一次悬停位置所采集的图像结果，实线部分表示第二次悬停位置所采集的图像结果。其中，小矩形框表示红外图像覆盖的位置，大矩形框表示广角图像覆盖的位置。

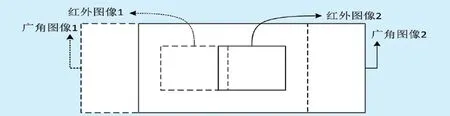
图1 红外及广角图像位置对应关系示意图。

为得到缺陷在红外图像上的准确位置，使用高精度深度学习模型对红外图像进行缺陷检测，得到缺陷类型及缺陷在红外图像上的位置范围框，并获取位置范围框的中心位置坐标。接着，按照双光相机的参数，以及红外图像与广角图像的特征对应关系，计算仿射变换矩阵。然后，按照仿射变换矩阵，将每个缺陷的缺陷点中心坐标由红外图像映射到广角图像。设红外图像上的二维坐标为（xir，yir），对应的广角图像的二维坐标为（xwa，ywa），i，j为旋转参数，k为平移参数，则对应的变换公式为：

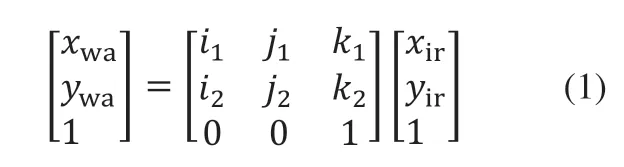
经过公式（1）计算得到广角图像上的缺陷点坐标。相较红外图像，广角图像之间的重叠区域更大，可以更好地进行空三运算。因此将缺陷坐标从红外图像坐标系换算到广角图像坐标系后，后续运算在广角图像坐标系下进行，即下文中的坐标转换流程。

坐标转换流程

总体坐标转换流程如图2所示。

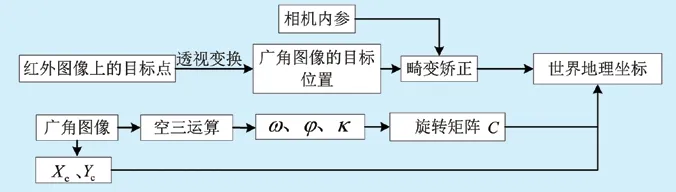
图2 总体坐标转换流程。

首先对所有广角图像进行空三运算，得到精确的相机拍摄位姿（欧拉角）；然后结合无人机相机云台位置计算拍摄点的相机坐标，得出广角相机拍摄中心的地理坐标X、Y，高程信息Z，以及相机姿态角ω、φ、k,具体过程如下所述。

第一，获取无人机采集广角图像时的悬停位置经度、纬度、绝对高程，以及红外图像中心点在相应地理位置上对应的绝对高程信息。

第二，结合双光相机的内部参数，对广角图像的畸变进行校正,同时根据旋转轴的顺序，计算旋转矩阵。设中心位置坐标为（x，y），双光相机的几何中心坐标为（x0，y0），广角图像宽为w0，拍摄焦距为f，拍摄中心距相机的距离为d,校正过程如下：

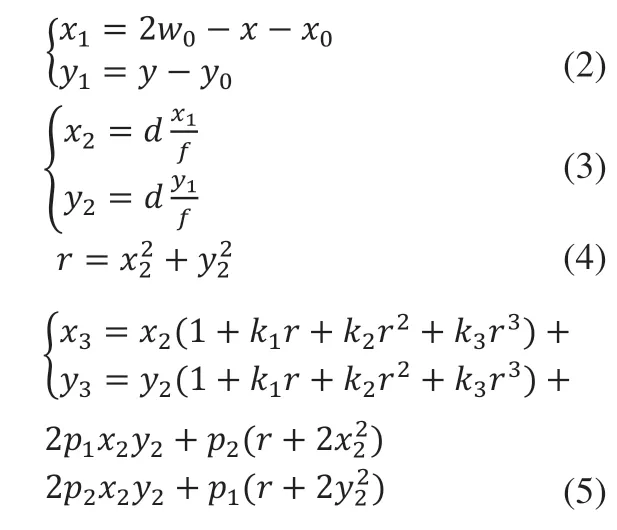
在公式(5)中，k1，k2，k3表示双光相机径向畸变的泰勒展开系数，p1、p2表示双光相机切向畸变的系数。接着，根据空三计算得到的相机姿态角ω、φ、k,计算旋转矩阵C,其中：

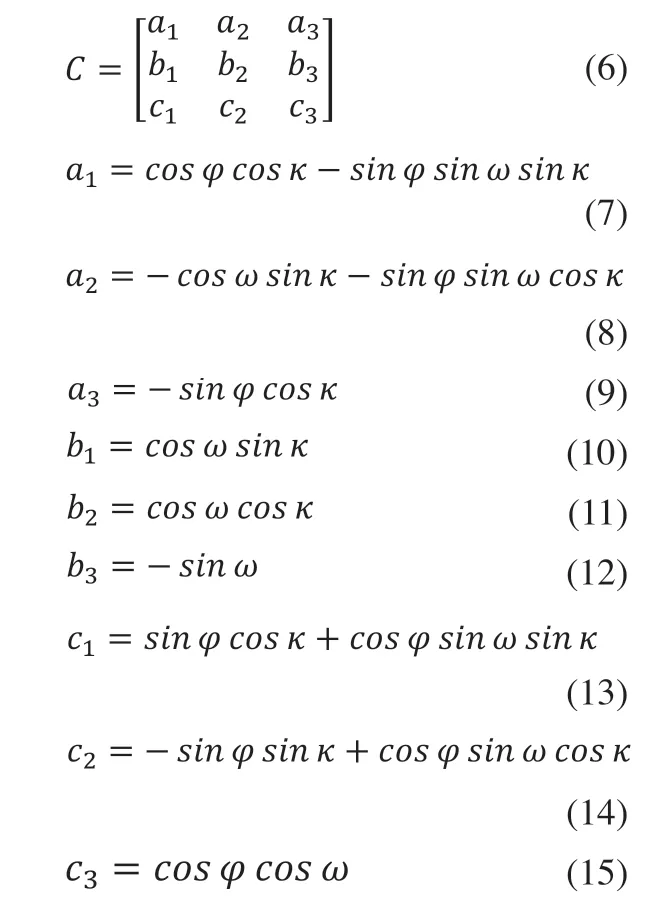
第三，根据旋转矩阵C、广角图像拍摄中心点的世界坐标系的地理坐标，计算得到缺陷地理坐标：

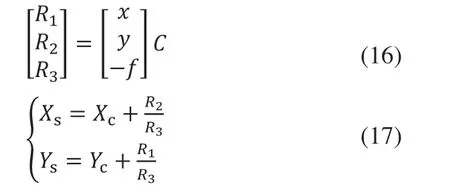
其中，公式（16）中的（x，y）是经过公式（5）畸变校正后的结果，在公式（17）中，（Xs，Ys）表示缺陷地理坐标，（Xc，Yc）表示广角图像拍摄中心点的世界坐标系的地理坐标。

降重处理

降重过程如图3所示。

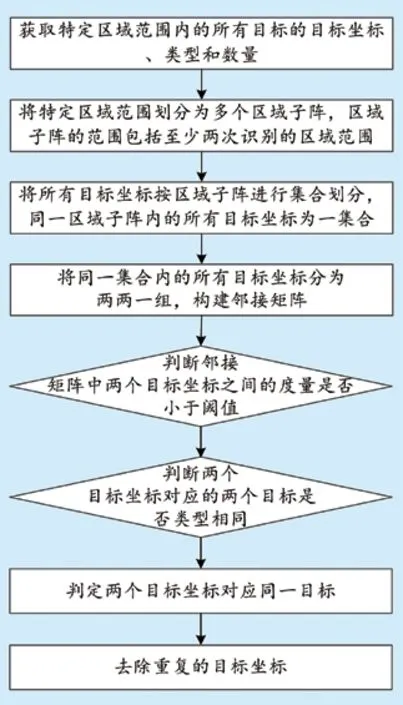
图3 缺陷降重过程。

经过图像坐标向地理坐标转换之后，得到N个缺陷点的地理坐标。为根据缺陷点的位置进行降重处理，首先构造一个N×N的邻接矩阵，邻接矩阵中的第i行的N个数值依次为第i个目标坐标分别与第1-N个目标坐标之间的度量，i为1，2…N，其中距离度量采用L2距离进行度量，即：

以N为4为例，邻接矩阵定义为A。

其中，邻接矩阵中的第1行的4个数值分别为：第1个目标坐标和第1 ～4个目标坐标之间的度量a11，a12，a13，a14。

第2行的4个数值分别为：第2个目标坐标和第1 ～4个目标坐标之间的度量a21，a22，a23，a24。

第3行的4个数值分别为：第3个目标坐标和第1 ～4个目标坐标之间的度量a31，a32，a33，a34。

第4行的4个数值分别为：第4个目标坐标和第1 ～4个目标坐标之间的度量a41，a42，a43，a44。

邻接矩阵构建完成后，判断邻接矩阵中两个目标坐标之间的度量是否小于阈值。其中，邻接矩阵中两个目标坐标之间的度量阈值可以根据实际应用场景进行设置。以特定区域范围为光伏电站，光伏电站内设置有多个光伏组件，各光伏组件的尺寸相同，阈值Th与光伏组件宽度W之间的大小关系为：W≤Th≤2W。光伏组件通常为矩形，光伏组件宽度W指的是矩形中较短的边尺寸。在该应用场景中，以上阈值Th大小的设置可以兼顾较好的去重效果，以及避免不当去重造成的目标坐标缺失。遍历邻接矩阵中的各数值，将各数值分别与阈值Th进行比较。例如，邻接矩阵中a12的数值为0.1，阈值为0.2，则a12小于阈值，说明第1个目标坐标和第2个目标坐标之间的度量小于阈值。若邻接矩阵A中两个目标坐标之间的度量小于阈值，则可能说明一个目标被识别2次，若邻接矩阵中三个目标坐标之间的度量小于阈值，则可能说明一个目标被识别3次。若两个目标的目标坐标之间的度量小于阈值，且类型相同，则判定两个目标坐标对应同一目标，也就是在识别过程中，同一个目标被重复识别。若两个目标的目标坐标之间的度量小于阈值，但类型不同，则表示两个目标为不同目标，不存在重复识别的问题。每个目标坐标与自身之间的度量值均为0，即a11、a22、a33和a44均为0，在邻接矩阵A中可直接记录为“0”，且第1个目标坐标与第2个目标坐标之间的度量a12，与第2个目标坐标与第1个目标坐标之间的度量a21相同。类似地，a13和a31相同，a14和a41相同，a23和a32相同，a24和a42相同，a34和a43相同，则邻接矩阵A中的以上相同数值只须计算一次，无须重复计算。

实验结果分析

为验证本文方法是否能准确定位且保证重复性，选取青铜峡光伏电站进行数据统计并对本文所用方法进行实地试验。为了分别评测本文方法的定位准确度和低重复性，首先分别定义不同指标进行评测，对于重复度的度量，定义重复个数Re为：

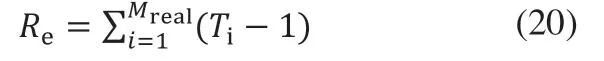
在公式（22）中，Mreal表示实际缺陷数，Ti表示在第i个缺陷对应的组件区域中所包含的缺陷个数，相应的定义准确率为：

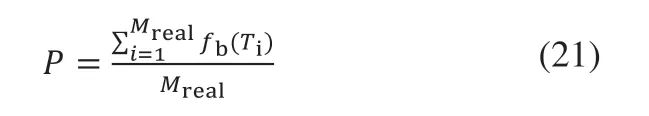
在公式（21）中，fb表示二值函数，即统计实际对应的缺陷组件所在区域中是否包含同类型缺陷，如果包含则记为1，否则记为0。

为了降低外界环境因素对实验结果的影响，分别在不同日期对该光伏电站进行巡检，其巡检时间及实际缺陷数如图4所示。在不同日期共完成4次巡检，然后分别将无人机正常采集数据、空三运算采集的准确率结果和本文有交叠的采集数据进行对比，如表1所示。从表1可以看出，在所有日期采集的数据，本文方法的准确率均高于常规巡检方式。此外，按照本文方式，将去掉空三运算之后的计算准确率进行消融对比，由表1数据可知，几乎所有使用空三计算的欧拉角转换数据，所得到的准确率均比无空三计算的方式要高。由此说明，在相机坐标转换过程中，使用空中三角测量方法计算转角具有必要性。

表1 不同巡检时间的准确率。

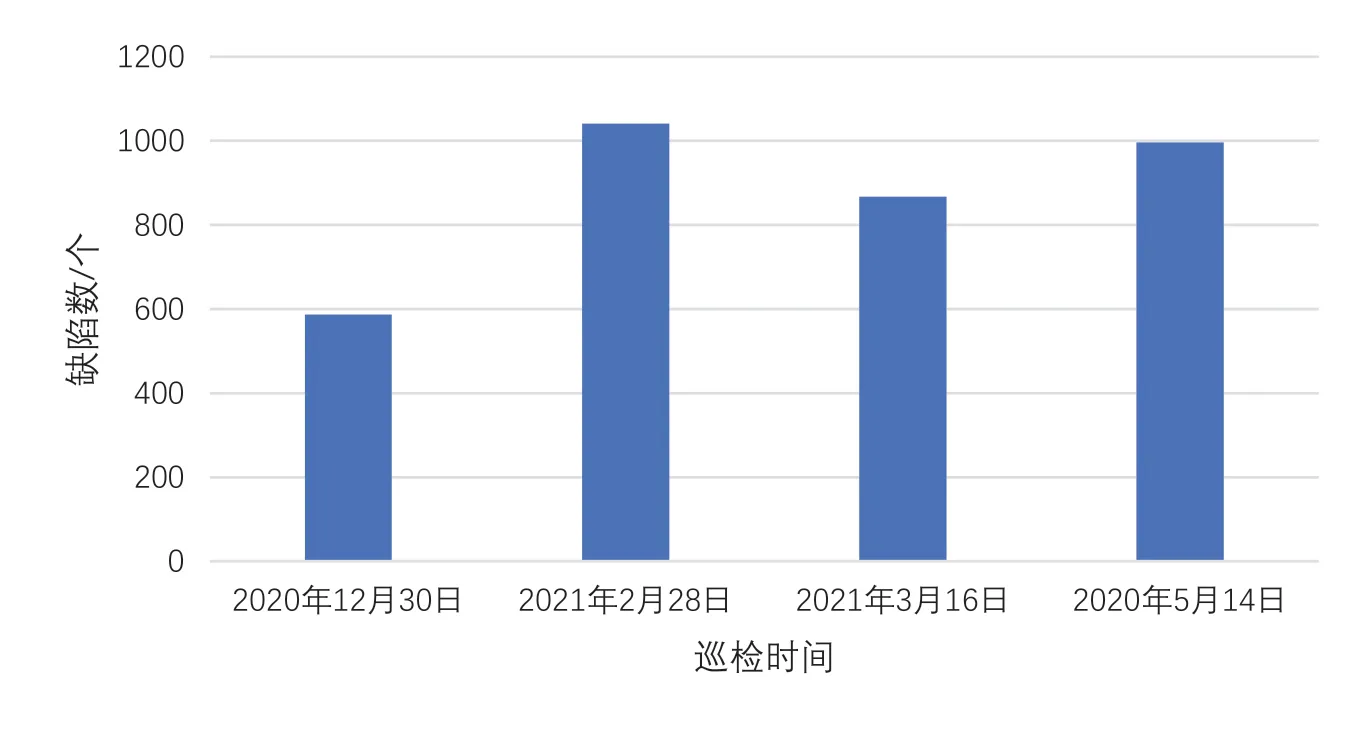
图4 巡检时间及实际缺陷数。

由于本文所用交叠数据采集方式会带来一定的缺陷重复定位，因此有必要验证去重处理后的缺陷个数的正确性。表2分别列出了去重前的重复缺陷个数和去重后的缺陷重复个数，接下来对比本文所用方法的重复率与常规巡检方式的重复率，重复率的计算式为公式(22)。

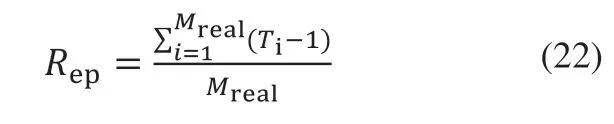
表2中的重复个数显示，在不同巡检日期得到的缺陷去重前后数据表现上，缺陷个数重复率均大幅降低，直接说明了本文去重方法的有效性。重复率结果表明，本文方法的重复率与常规巡检方式相差不多，间接说明了本文所述图像采集方式并没有带来额外的缺陷重复。

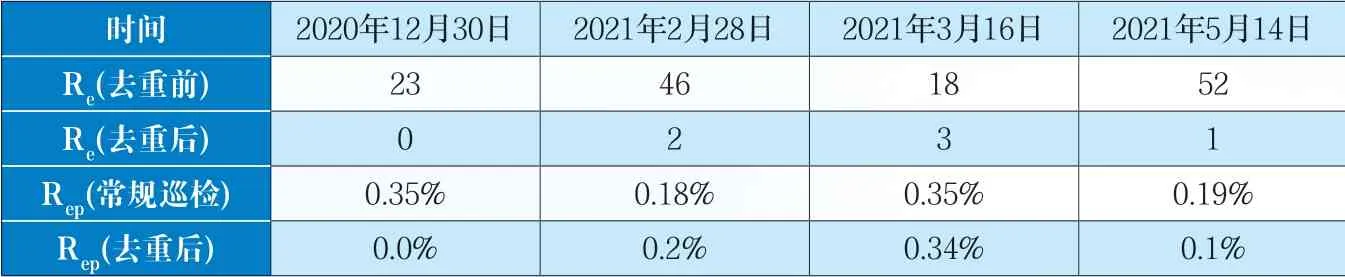
表2 重复率对比实验结果。

结论

针对无人机光伏电站缺陷巡检系统，本文提出了一种准确的缺陷地理坐标定位方法，能够为光伏电站运维人员提供有效的消缺及维护依据，相较常规无人机巡检提供的缺陷位置，本文方法具有更高的参考价值。本文研究成果主要包括三个方面。

第一，在数据采集过程中，利用双光相机采集光伏电站有交叠的红外图像和广角图像，为实现精确坐标转换提供数据基础。

第二，结合空中三角运算，修正无人机拍摄位姿（欧拉角），提升了相机坐标转换精度。

第三，对转换好的地理缺陷进行去重处理，减少了图像采集过程中因交叠产生的重复缺陷个数。■