电力机车牵引传动系统的多模式调制策略及切换方法研究

苑国锋，陈栋，郑春雨

(1.北方工业大学 变频技术北京市工程研究中心，北京 100144；2.北方工业大学 北京市电力节能关键技术协同创新中心，北京 100144)

0 引 言

近年来我国轨道交通行业发展迅速，成为继德、法、日之后掌握核心技术的少数国家之一。其中牵引传动调制策略和切换方法研究具有重要意义。

受散热和空间装配等方面的影响，牵引变流器最高开关频率一般只有几百赫兹。随着牵引电机输出频率升高，载波比(调制波频率和载波频率的比值)下降，电机电流低次谐波含量逐渐增加，此时普通的异步调制模式无法满足运行需求，需要采用同步调制策略来消除电机输出的非特征次谐波。目前主流的同步调制策略主要有同步SVPWM、特定谐波消除PWM以及电流谐波最小PWM。同步SVPWM调制具有转矩脉动小，易于数字化实现等优点[1]；SHEPWM和CHMPWM作为优化PWM，在低次谐波消除方面更占优势[2-3]，这两种调制方式需要离线计算开关角，其中，SHEPWM开关角的计算较为简单，且角度随着调制比连续分布，相对于其他优化PWM更易于实现。

对于上述两种调制算法，国内外已有大量研究，文献[4-5]详细介绍了同步SVPWM的基本原理和策略；文献[1]在此基础上对低开关频率下的SVPWM调制策略进行了比较；文献[6]提出了一种遗传算法和模拟退火算法相融合的方式来求解SHEPWM的开关角。文献[7]比较了不同开关角个数下的SHEPWM的电流谐波以及转矩脉动；文献[8]对SHEPWM的原理和切换策略进行了阐述；文献[9]对大功率牵引变流器中频区的调制算法进行了对比研究，指出优化同步调制具有更好的谐波特性。

在牵引控制系统中，一般采用多种调制模式相结合的方式以保证机车在载波比大范围变化的情况下实现全速度范围的平稳运行。文献[10]将异步SVPWM和SHEPWM两者结合的混合调制算法应用到机车牵引系统中。文献[11]采用异步SVPWM和同步SVPWM的混合调制模式。文献[12]通过FPGA将由异步SVPWM、同步SVPWM和CHMPWM三者结合而成的混合调制模式应用到电力机车牵引系统。

上述文献分别论述了各种调制方式的原理和实现方式，并对不同调制模式之间的切换方法进行了阐述。为了减小切换过程产生的电流冲击，一般选择相电流响应的暂态分量为零处进行切换，即相电压基波相角的90°或270°，但该策略需要三相独立切换[8]，实现较为复杂。

矢量控制算法和同步调制相结合时，固定的采样点和等步长的中断之间产生了矛盾，文献[10]将控制和调制算法分开设计，控制频率固定，并通过一个相角控制器来保证调制算法和控制算法的电压矢量相位一致，实现了牵引机车的有速度传感器运行。文献[11]通过锁相环的方式，消除了控制算法和调制算法间的相角误差并将其应用于永磁同步电机上，实现了闭环控制。国外Holtz教授在大功率传动控制算法方面有比较深入的工作，文献[13-15]对低开关频率下的闭环控制以及调制算法的动态性能改善做了比较多的研究。上述文献的PWM方案在数字化实现的时候需要2个中断，一个用于控制算法，另一个用于调制算法，其实现复杂，且需要消耗较多的芯片资源。

本文主要针对多模式调制策略在电力机车牵引系统中的应用进行研究。首先，提出一种异步调制切换至同步SVPWM再切换到SHEPWM直至方波的多模式调制策略，并提出可实现不同调制模式间三相同时过渡且不引起大电流冲击的切换点选择方法。其次，提出了在统一框架下设计电机控制策略和调制算法的方法，避免了两者之间相角不匹配的问题，且在实现过程中仅采用一个中断，节省了芯片资源。最后，在统一框架下的进行了调节器及观测器的设计，实现牵引系统无速度传感器运行并进行实验验证，结果验证了算法的有效性。

1 多模式PWM调制策略

1.1 调制策略采样点及采样频率设置

为充分利用各调制方式的优点，本文提出了一种异步SVPWM—同步SVPWM—SHEPWM的多模式调制策略，即在低速区使用异步SVPWM，中速区使用同步SVPWM，高速区使用SHEPWM直至方波区。

同步SVPWM实现中，零矢量和有效电压矢量的不同组合构成了不同的PWM模式[4]，主要有传统空间矢量策略(CSCV)，基本母线钳位策略(BBCS)以及边界采样策略(BSS)三种。本文在载波比为15时采用CSCV调制策略。以第一扇区为例，采样点设置如表1所示。

表1 同步SVPWM采样点

SHEPWM通过计算开关角的方式来消除特定次谐波。对满足三相对称，四分之一周期偶对称以及半波奇对称的PWM电压波形进行傅里叶分析，可以得到不同次数谐波电压幅值的表达式。联合要消除的特定次谐波表达式，建立对应的电压方程，通过经验公式给定初值，可最终求得开关角。区别于同步SVPWM，SHEPWM的开关角是离线计算出的固定值。为实现SHEPWM，本文以10°为一个采样周期，每个周期的采样点设置在区间中点位置处，如5°、15°、25°等。

根据同步SVPWM和SHEPWM设定的采样点，为满足后续控制算法和调制算法的统一，设计不同PWM模式下的控制系统采样频率如表2所示，其中f表示电机同步频率。

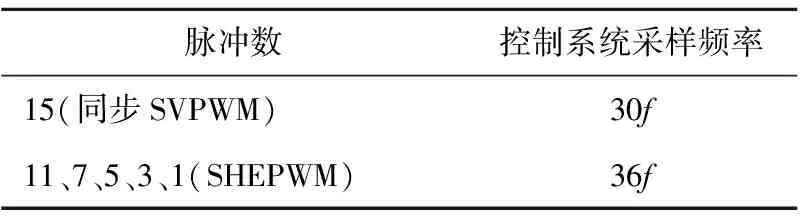
表2 多模式PWM下的采样频率

基于上面的分析，在全速域内采用了如图1所示的调制策略。当电机输出的同步频率低于30 Hz时采用SVPWM调制策略，在大于30 Hz时采用SHEPWM调制策略，直至方波区。

图1 多模式PWM调制策略

1.2 不同调制模式的切换方法

从电流谐波的角度来看，在保证不同模式间的电压矢量相位连续，且能避免谐波电流的冲击的状况下，即可实现不同调制模式间的平稳切换。

由于异步模式和15脉冲同步SVPWM使用的都是CSVS策略，在每个采样周期末尾，谐波电流均为0，因此只要在载波比为15处设置切换点即可平滑过渡。

对于SHEPWM间的切换，本文从磁链连续的角度出发，寻找适合三相同时切换且不会产生明显电流和转矩冲击的最优切换点。

电机的转子磁链和电磁转矩的表达式为：

(1)

(2)

其中：Te表示电机的电磁转矩；ψs和ψr分别表示定子和转子磁链矢量；Lm、Ls以及Lr分别表示电机互感、定子电感以及转子电感；ψrd表示按照转子磁场定向后的转子磁链幅值；np表示极对数；Tr和σ分别表示转子时间常数以及漏磁系数，具体表达式如下：

Tr=Lr/Rr;

(3)

(4)

其中Rr表示转子电阻。

由式(1)、式(2)可知，电磁转矩等于转子磁链和定子磁链的叉积。在转子磁场定向的条件下，转子磁链的幅值和d轴电流之间是截止频率比较低的一阶惯性环节，因此只需要考虑定子磁链对转矩的影响。如果在切换点处，两种PWM模式的定子磁链轨迹相同，则切换时电机转矩就不会发生脉动。切换点的选择应该保证切换前后两种调制方式对应的磁链轨迹连续且切换后的磁链轨迹的中心不发生较大偏移。

图2为动态过程中，SHEPWM 11脉冲、7脉冲、5脉冲以及3脉冲模式下的定子磁链轨迹图。根据磁链轨迹的对称性，参照SVPWM的扇区划分方式，可将SHEPWM的磁链轨迹分成6个区，图中“I”表示其中的一个区。

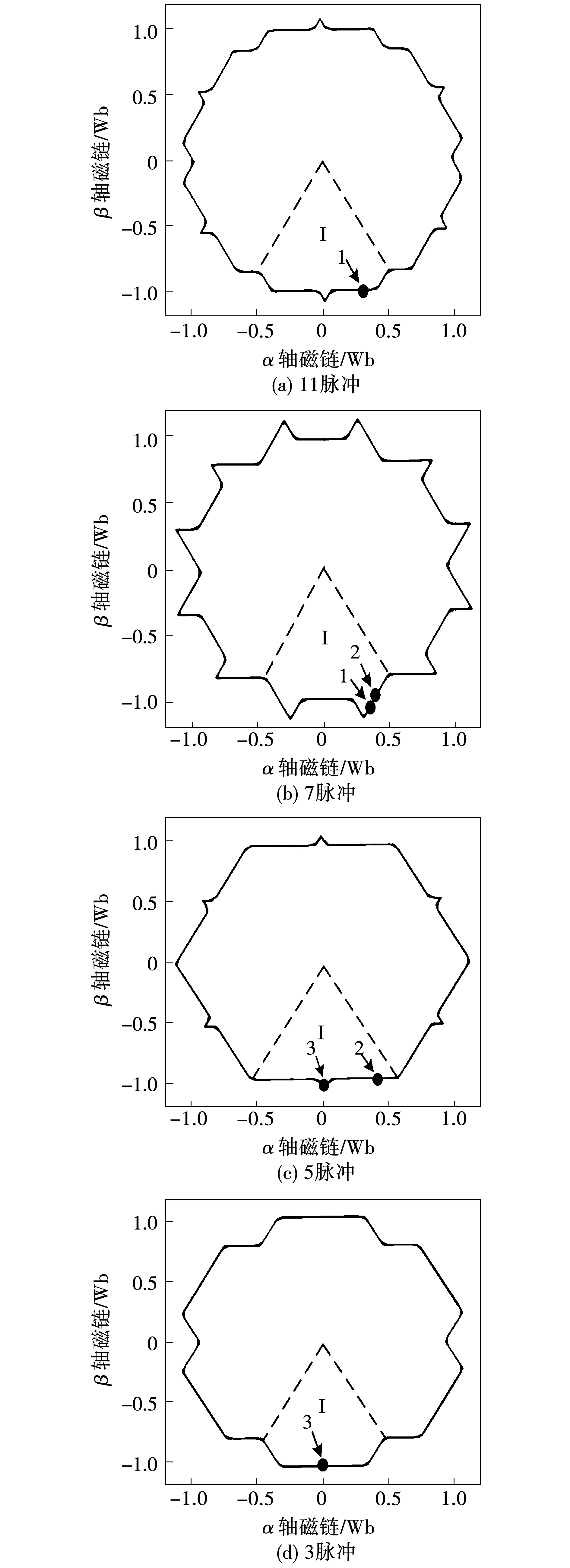
图2 11脉冲、7脉冲和3脉冲磁链轨迹图

以11脉冲和7脉冲磁链轨迹为例，虽然SHEPWM的开关角都是离线计算的结果，但是通过观察发现，最终作用在电机上的电压矢量表现形式类似于空间矢量调制，根据文中磁链轨迹的区域I，其对应的电压矢量作用序列如图3所示。

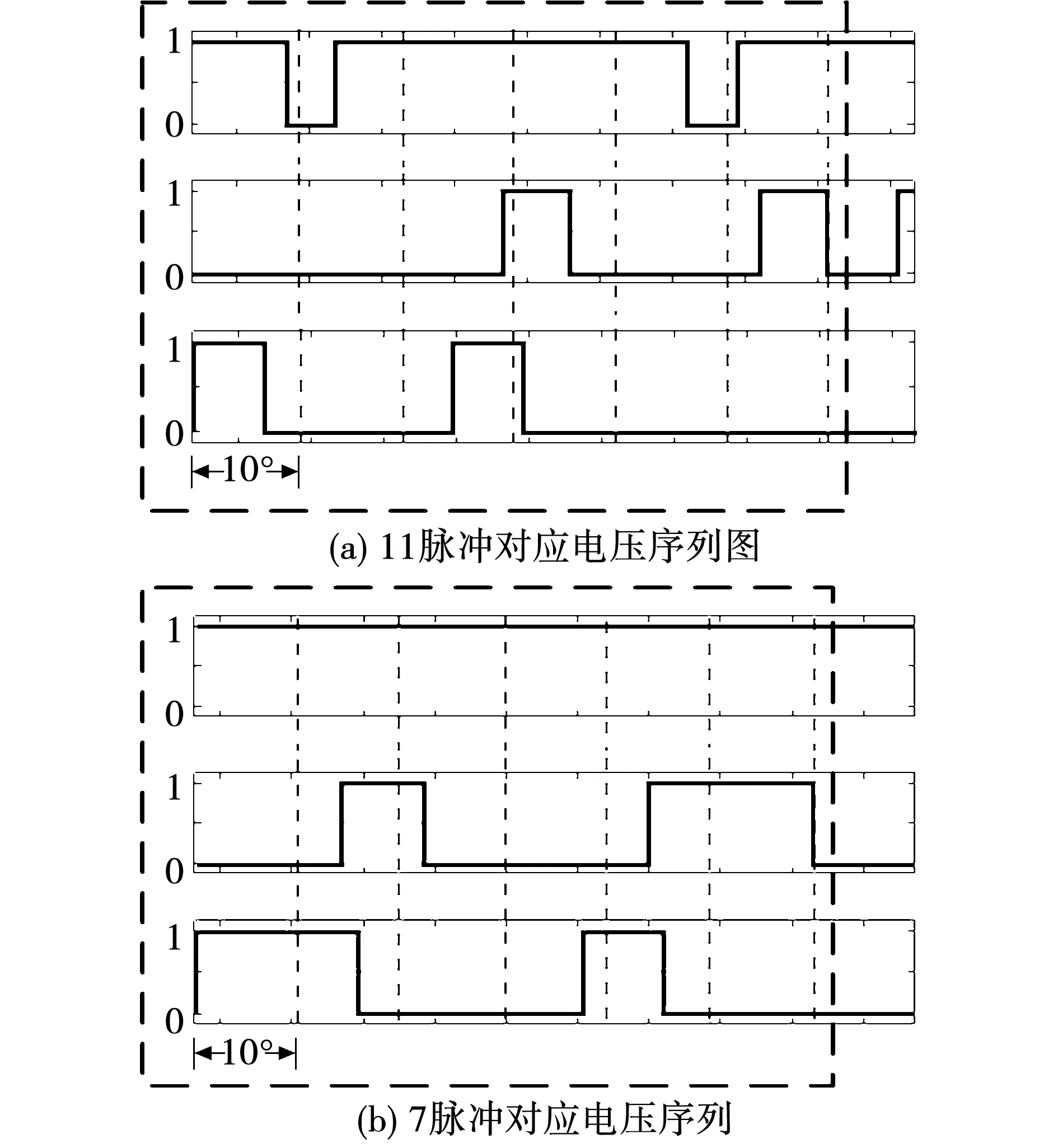
图3 11脉冲、7脉冲的电压序列

根据图3(a)可知，11脉冲的在区域I的电压矢量作用顺序为：101→100→000→100→101→111→110→100→000→100→110，从上面的开关序列可以看出，矢量切换时均只有一相状态发生变化，这一特征和SVPWM相同。

同样的，根据图3(b)可知，7脉冲在区域I的电压矢量作用顺序为：101→111→110→100→101→111→110。在选择切换点时应依照磁链轨迹连续的原则，概括为以下两点：第一，在切换点附近，两种不同的模式磁链轨迹相近；第二，切换完成后不能造成新的磁链轨迹的中心偏离原点。根据上述的原则，如果能在两者磁链轨迹的交叉点处进行切换，则可以实现完全无冲击，但这点较难实现。通过观察可以发现，在图3所示的区域中，11脉冲最后10°的有效电压矢量序列为100→110，7脉冲的有效矢量顺序为110。最后10°磁链轨迹如图4所示。

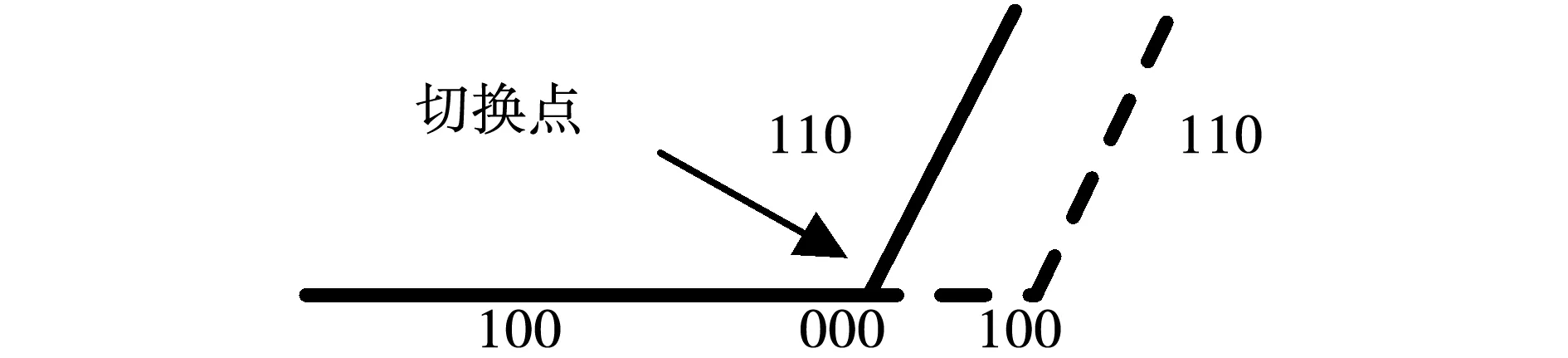
图4 11脉冲切7脉冲磁链轨迹图

图4中虚线表示11脉冲磁链轨迹图，如果在最后10°进行切换，相当于电压矢量提前由100变为110，切换后的磁链轨迹变化如图4中实线所示。因此选择在最后10°切换，满足上述依据磁链轨迹连续的切换原则，不会引起太大的切换冲击。根据对称性，其他的5个区域具有同等效应。

其他模式之间的切换同样可以依据上述原则进行切换点选择，按照图2中的磁链轨迹可知，5脉冲在右半平面侧磁链轨迹对应的电压矢量几乎都是100，因此7脉冲和5脉冲切换点可以选在两者磁链交点附近，即每个区的最后10°，同样的，5脉冲和3脉冲选在每个区的中间20～30°。

通过上面的分析，在两种模式采样点和采样频率相同的情况下，11脉冲和7脉冲的切换点可以选在图2(a)中1号点所在采样周期，即“I”区的最后10°；同样的，7脉冲和5脉冲的切换点可以选在图2(b)中2号点所在采样周期，即“I”区的最后10°；5脉冲和3脉冲的切换点可在图2(c)中3号点所在的采样周期，即“I”区中间20～30°。根据对称性，其他的5个区切换点的位置和“I”区的位置一致。最后，因为SHEPWM的开关角计算以及实现方式不尽相同，具体的切换点位置可以在上述分析的基础上作相应调整。

对于SHEPWM而言，当开关角个数大于3时，因电机电感的滤波作用，电流谐波已经很小，15脉冲(同步SVPWM)和11脉冲(SHEPWM)的切换点可以选在两种模式采样点接近的地方，这样就不会引起太大的电流冲击。

按照上述原则选取的切换点进行仿真，结果如图5所示。

图5由上到下依次为线电压、电流以及转矩的仿真波形。从图5(a)和图5(b)的转矩波形图中可以看出，在切换处并没有引起较大的转矩波动，实现了不同模式之间的平稳切换。

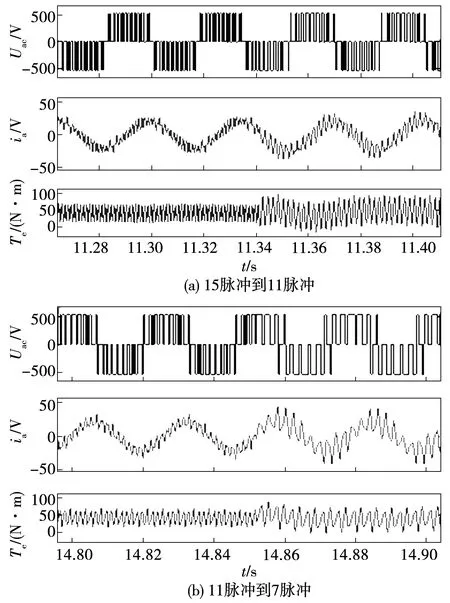
图5 11脉冲到7脉冲的仿真波形

2 统一框架下的控制算法

异步调制和同步调制本质的区别在于，前者是等步长采样，而后者是等相位差采样。使用异步调制的电机控制算法采样频率固定，控制和调制可以在同一个中断中执行。而同步调制采样点固定，因此在应用同步调制时，需要解决固定采样点和等步长中断之间的矛盾。按照上节统一框架设计的思想，通过合理设置采样点和采样频率，使系统采样频率随调制波频率同步变化，实现了电机控制策略和调制策略在同一中断运行。基于统一框架方法设计的控制系统采样频率会随电机输出同步频率变化，因此整体采样频率较低，这会影响到系统的控制带宽和输出性能，因此本节论述适用于低采样率下的电流调节器、磁链观测器和速度估计方法。

2.1 电流调节器

传统的矢量控制系统中，大多采用线性PI调节器，在设计调节器参数时，受离散化的误差以及建模的精准程度的影响使得传统线性PI调节器很难实现转矩和磁链的完全解耦，从而导致传统PI调节器在高速区性能变差；同时当控制系统的采样频率下降时，传统PI调节器的控制带宽进一步下降，最终导致系统变得不稳定。

复矢量调节器将d、q轴电流当做一个整体，与传统方法比具有更优的控制性能和参数鲁棒性[13]，由于实际应用中大都采用数字控制系统，为避免离散化带来的误差，同时提高低采样率下的电流环带宽[16]，本文采用直接在离散域设计的电流调节器。考虑一拍延时的基于转子磁链定向的电流环数学模型为

(5)

式中：Tsc是采样周期；Td表示控制系统的延迟；ωe表示同步角频率；Rσ=Rs+(Lm+Lr)2Rr；Lσ=σLs。

基于上述模型设计的离散域电流调节器为

(6)

2.2 磁链观测和转速估计

本文利用龙贝格全阶观测器，对转子磁链的信息进行观测，观测器的结构框图如图6所示。该观测器是以定子电流和转子磁链作为状态变量。根据电机的状态方程，利用可测量的定子电压Us和定子电流is来重构状态变量——转子磁链ψr，其中Usα、Usβ和isα、isβ以及ψrα、ψrβ分别表示定子电压、定子电流以及转子磁链的α、β轴分量。上标“^”表示估计量。静止坐标系下，观测器状态方程表达式为

图6 速度自适应磁链观测器

(7)

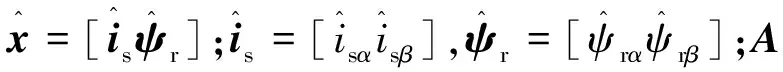
通过合理的选择增益矩阵G，可以控制系统的动态性能，确保观测器的收敛性和稳定性。由于电机是稳定的物理系统，一般选择增益矩阵使观测器的极点正比于电机的极点Po=kPI(Po表示增益矩阵的极点，PI表示电机的极点)，k>1以保证观测器的稳定性和收敛速度。

按照这种方式选取的增益矩阵会使观测器极点的虚部在电机高速运行时较大。此时阻尼比较小，因而容易发生震荡。为改善这一缺点，本文采用将观测器极点配置在电机极点左侧的方式选取增益矩阵，即Po=PI+b，其中，b=-40，同时令ωr→∞，对应的增益矩阵可以化简为[17]

(8)

利用基于上述观测器的误差方程，构造李雅普诺夫函数，根据李雅普诺夫稳定定律，可以得到满足观测器收敛的转速自适应率[18]为

(9)

式中：Δis为实际电流和观测电流的误差；ks为正常数。对上式进行积分即可估计出电机的转速，从而实现电机的无速度传感器运行。在实际应用中，通常采用PI调节器来代替纯积分以保证算法的可靠性。

3 实验验证

3.1 控制框图

实验采用基于转子磁场定向的混合矢量控制算法，控制框图如图7所示。

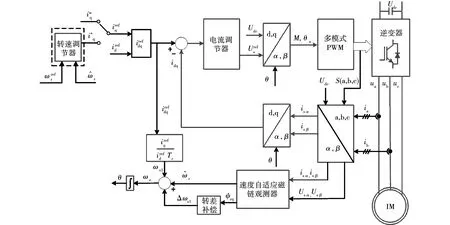
图7 系统控制框图

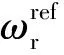
3.2 实验结果

实验用牵引电机为模拟实际的地铁运行工况，电机与转动惯量为4.85 kg·m2的飞轮相连。实验平台如图8所示，是按照真实牵引系统等比例缩小的实验平台；电机的详细参数如表3所示。

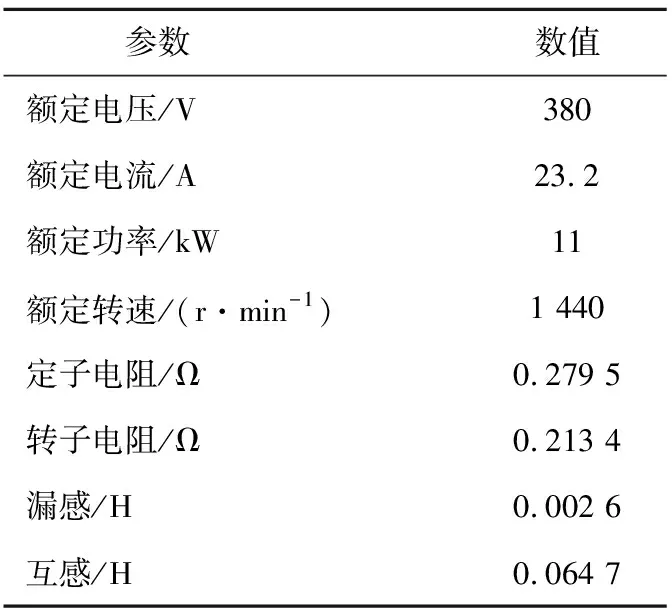
表3 电机参数

图8 牵引实验平台

牵引电机采用转矩控制的模式，给定转子磁链的幅值为0.987 6 Wb，转矩电流给定为14 A，电机从静止加速到方波模式线电压和相电流波形以及不同模式之间切换的线电压和相电流波形如图9所示。从图中可以看出，随着电机的输出频率持续的上升，电机的调制模式从异步SVPWM切换到同步SVPWM-SHEPWM直至方波。整个过程中，不同调制模式间的切换较为平稳，没有出现明显的电流波动现象，验证了前文所述切换点选择方法的有效性和正确性。

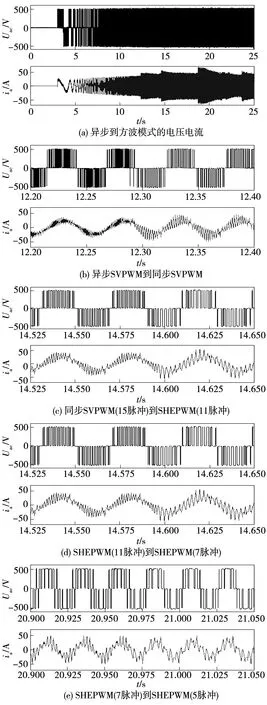
图9 不同调制模式切换的电压电流波形

为了验证统一框架下调节器和观测器的有效性，进行了速度观测和转矩电流指令跟踪的实验。在实际的牵引系统中，给定指令为转矩指令。根据牵引系统加速度和减速度指标要求，转速指令通过斜波给定，对应的转速响应亦为斜坡响应。该实验中，转速斜坡为每秒升速75.65 r/min，实际对应转矩大小为38.5 N·m，观察电机从静止加速到1 740 r/min，再由1 740 r/min制动减速至静止的过程中电流和转速响应。图10为此动态过程中转速和电流的波形。

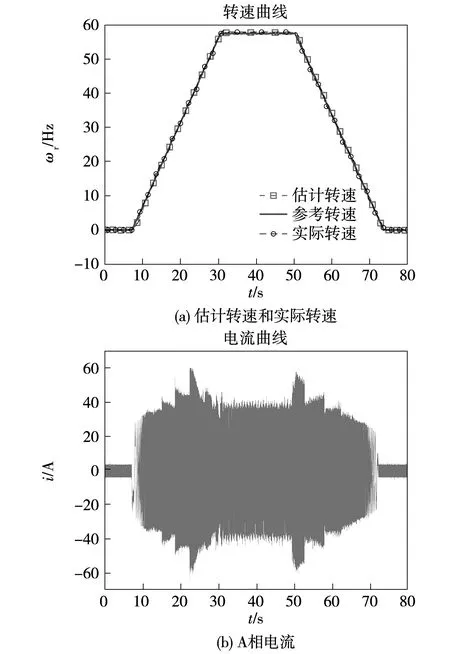
图10 牵引和制动工况下电机转速和电流

图10(a)中粗实线为给定转速，正方形标记线为估计转速，圆形标记线为扭矩仪测量出的实际转速。从图10可以看出，估计转速和实际转速曲线几乎一致，验证了从静止加速至方波工况下转速估计的有效性。

为模拟实际运行工况，在仅保留电流环情况下进行实验。图11为给定的转矩电流和反馈的转矩电流的比较。程序中转矩电流通过斜坡的方式给定，图中红线表示给定幅值大小。从图中可以看出，反馈的q轴电流经过一个斜坡后达到给定值，实现了对转矩电流的准确控制。

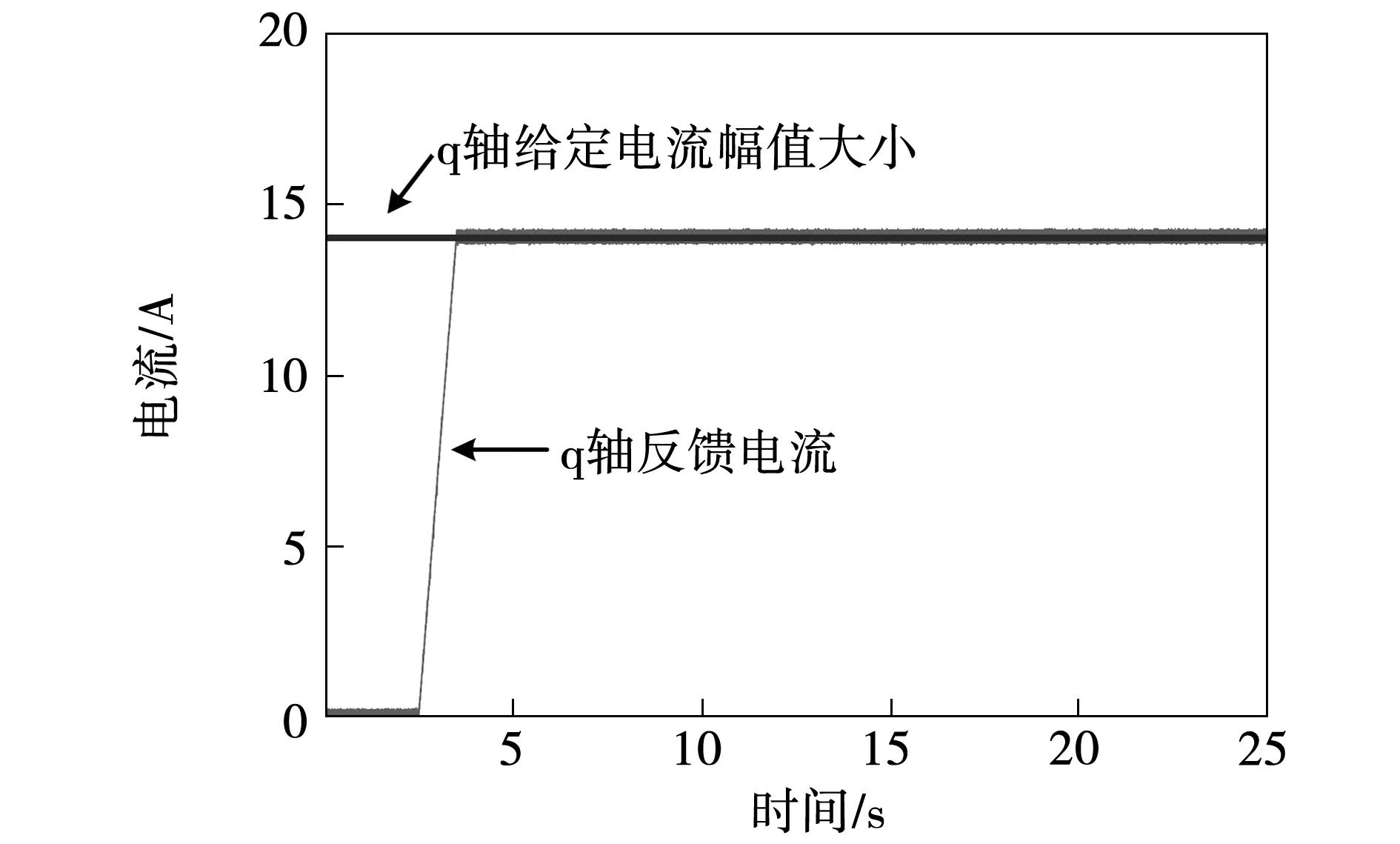
图11 转矩电流给定和反馈

4 结 论

针对大功率牵引电机传动系统的实际应用工况，对低开关频率下的调制算法进行了研究；针对不同调制模式的特点，提出了适用于全速域的多模式调制策略；针对不同模式间的切换问题，从磁链连续的角度出发，根据磁链轨迹，选出最优的可三相同时切换的过渡点，确保了不同模式间的平稳切换。针对同步调制算法和控制算法存在的相角匹配问题，通过合理设置采样点和系统采样频率实现二者的统一，提出了统一框架设计方法，论述了下低采样率的电流调节器和磁链观测器的设计。最后通过实验验证了所提出算法的有效性。