一种双输入高增益DC-DC变换器

林国庆，张宙

(福州大学 福建省新能源发电与电能变换重点实验室，福州 350116)

0 引 言

随着石油、煤、天然气等化石资源的日渐枯竭以及环境问题日益突出，以光伏、燃料电池、地热等为代表的可再生能源的利用越来越受到关注[1-4]。但是这些可再生能源存在供电质量差、受环境影响很大等缺陷，因此采用多种能源联合供电的系统可以有效地提高供电系统的可靠性和电能质量[5]。可再生能源的低电压通常是18～56 V，不宜直接并网发电或者给负载供电，所以需要直流变换器将较低的电压升到200～400 V或者更高的电压等级[6-11]，空间站卫星系统中通常需要把16～28 V的光伏电池电压通过高增益直流变换器提升到100 V。因此，研究多输入高增益直流变换器具有重要意义。

多输入高增益直流变换器可以分为隔离型和非隔离型两种。隔离型多输入变换器可以通过增大变压器的匝比提高电压增益，输入能量也可以灵活地分配，电路安全性较高，但是高的匝比会使得电路效率大大降低，还会使电路的体积和重量变大[12-15]。传统的非隔离型多输入变换器采用基本的BOOST电路在输出端并联，以实现多个能源独立和分时供电，这种电路可靠性高、控制简单，但是无法实现较高的电压增益。

文献[16]提出了一种无耦合电感非隔离多输入直流变换器。在该电路中，每个输入源对应一个输入模块，并且随着模块数目增加，变换器电压增益随之升高，但是每个输入模块都使用了较多的电感、电容和开关管，各开关管也不共地，因此该变换器的成本较高，体积较大，设计较为不便。

文献[17]所提变换器拓扑是基于二极管电容增压单元，该变换器结构与控制相对简单，理论上输入源数目可以无限增加并且各输入源相互独立，但是该拓扑电压增益较低，要实现较高变压比需要使用较多的增压单元，而且输入端串联的二极管会使得电路的效率大大降低。

文献[18]提出了一种集成的双输入直流变换器，该电路只使用了一个电感，因此电路体积和重量得到有效降低，但是所使用的3个开关管均不共地，与输入源串联的二极管增大了电路损耗，并且只有在输入源1的电压低于输入源2的电压时，电路才能正常工作，这些缺陷极大地限制了该变换器的应用。

文献[19-20]提出的双输入直流变换器均是基于BOOST拓扑，都采用二极管电容增压单元实现高的电压增益，控制简单，开关管电压应力较低，但是2种变换器均无法在单路供电时正常工作。

针对以上问题，本文提出了一种基于开关电容增压单元的双输入高增益直流变换器，通过引入开关电容电路，使两路输入源在单独或同时供电时均可以实现高电压增益，且具有电路简单、开关器件电压应力低、供电灵活等优点。

1 工作原理

本文提出的双输入高增益直流变换器拓扑如图1所示。输入电源Vi1、电感L1、开关管S1、二极管D1、D2和电容C1、C2构成一个单输入双输出的BOOST变换器，电感L1续流阶段同时给电容C1、C2充电；输入电源Vi2、电感L2、开关管S2、二极管D4和电容Co构成另一个BOOST变换器，电感L2续流阶段，电感与输入电源Vi2、电容C1、C2串联在一起给负载供电，从而获得较高的电压增益。

图1 双输入高增益直流变换器

为了简化分析过程，作出如下假设：

1)电感L1和L2足够大，电感电流连续；

2)所有器件均为理想器件；

3)电容C1、C2、Co足够大，其电压Vc1、Vc2、Vo稳态时保持恒定，且C1=C2。

根据输入端电源连接方式不同，电路可以工作在3种供电模式。

1.1 电源Vi1、Vi2同时供电工作模式

电源Vi1、Vi2同时供电时，变换器主要工作波形如图2所示。开关管S1、S2为交错控制，且2个开关占空比Ds1、Ds2满足Ds1+Ds2≥1，并且假设由Vi1供电的BOOST变换器增益足够高，其输出电压始终大于Vi2，二极管D3处于截止状态，在一个开关周期，变换器有4种工作模态，如图3所示。

图2 变换器主要工作波形

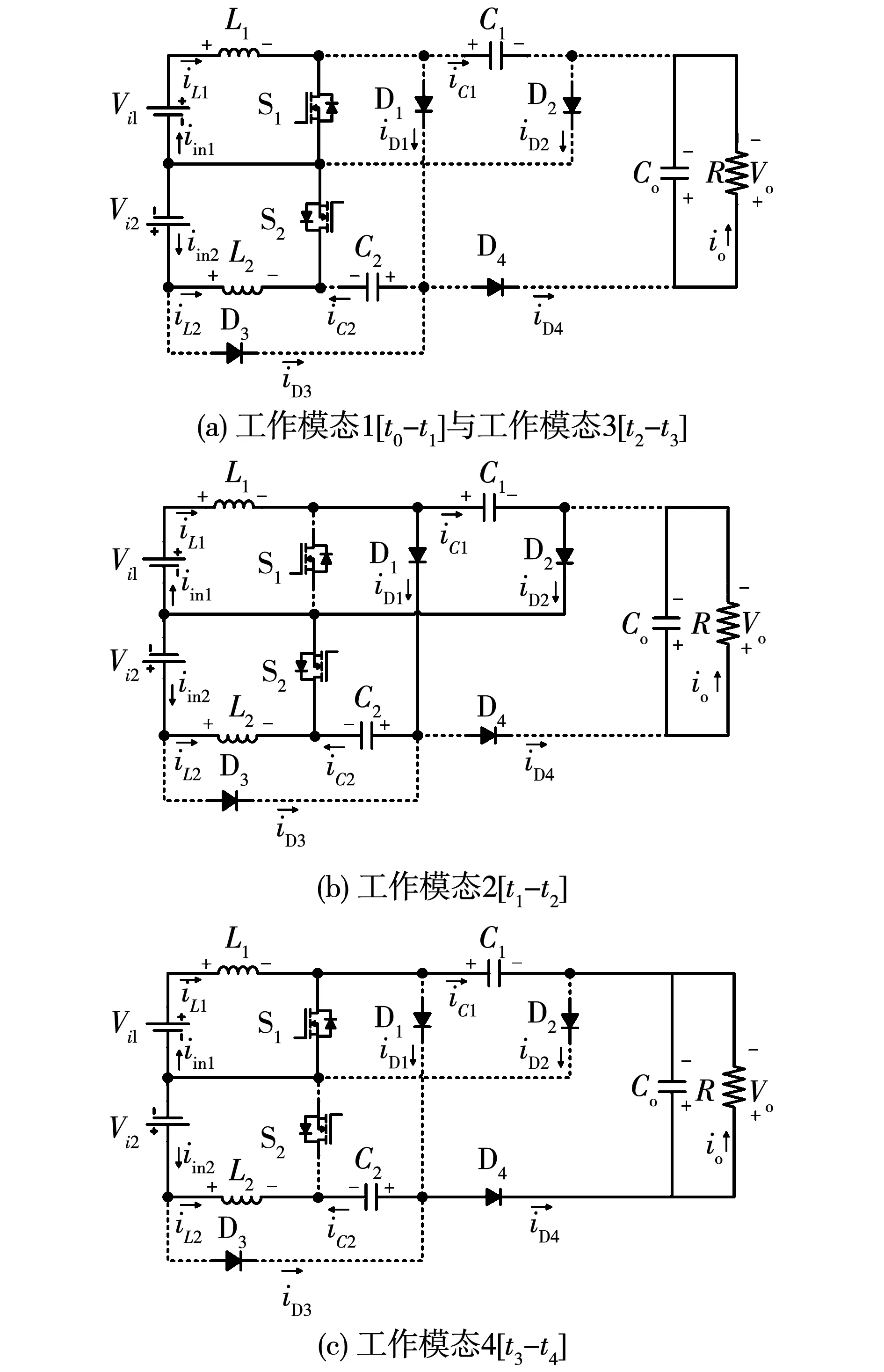
图3 Vi1、Vi2同时供电开关状态的等效电路

1)工作模态1[t0-t1]:t0时刻，开关管S2导通，S1继续导通，Vi2通过开关管S2给电感L2充电，Vi1通过开关管S1继续给电感L1充电，电感L1和L2的电流线性上升，4个二极管反向截止，输出电容Co给负载供电。

2)工作模态2[t1-t2]:t1时刻，开关管S1关断，S2导通，电感L1续流，其电流线性下降，此时续流路径有2条：①电感电流经过D2对电容C1充电；②电感电流经过D1、S2对电容C2充电。Vi2继续通过开关管S2给电感L2充电，电感L2电流继续线性上升。二极管D3、D4承受反压截止，输出电容Co给负载供电。

3)工作模态3[t2-t3]:此时运行状态跟模态1相同，不再重复分析。

4)工作模态4[t3-t4]:t3时刻，开关管S2断开，S1继续导通，电感L2与C1、C2、Vi2串联，经过S1和D4给输出电容Co充电，同时向负载供电，电感L2电流线性下降。Vi1继续通过开关管S1给电感L1充电，电感电流线性上升；二极管D2承受电容C1电压而反向截止。

1.2 电源Vi1单独供电工作模式

Vi1单独供电时，开关管S2一直导通，开关管驱动波形如图4所示，则一个开关周期内变换器有2种工作模态，如图5所示。

图4 开关驱动波形

图5 Vi1单独供电时开关状态的等效电路

1)工作模态1[t0-t1]:t0时刻，开关管S1、S2均导通，Vi1通过开关管S1给电感L1充电，电感电流线性上升，电容C1、C2串联经过S1、S2、D4给电容Co充电，同时给负载供电，二极管D2承受电容C1电压而反向截止，D3承受电容C2电压而反向截止。

2)工作模态2[t1-t2]:t1时刻，开关S1关断，S2继续开通，电感L1续流，电感电流线性下降，此时续流路径有2条：①电感L1电流经过D2对电容C1充电；②电感电流经过D1、S2对电容C2充电。二极管D3、D4承受反压截止，输出电容Co给负载放电。

1.3 电源Vi2单独供电工作模式

Vi2单独供电时，开关管S1一直关断，开关管驱动波形如图6所示，一个开关周期内变换器有2种工作模态，如图7所示。

图6 开关驱动波形

图7 Vi2单独供电时开关状态的等效电路

1)工作模态1[t0-t1]:t0时刻，开关管S1关断、S2导通，Vi2通过开关管S2给电感L2充电，电感L2电流线性上升，同时输入Vi2经过D3、S2给电容C2充电，二极管D1、D2、D4承受反压截止，输出电容Co给负载放电。

2)工作模态2[t1-t2]:t1时刻，开关管S2关断，S1仍然关断，电感L2续流，与Vi2、C2串联通过D2、D4给输出电容Co充电，同时给负载供电，二极管D1、D3承受反压截止。

2 性能分析

2.1 增益分析

基于上述分析，可以进一步求得3种供电方式下变换器的电压增益。

2.1.1 电源Vi1和Vi2同时供电情况

根据电感L1的伏秒平衡有：

(1)

可以得到：

(2)

(3)

根据电感L2的伏秒平衡有：

(4)

可以得到

(5)

假设两路输入电压相同，占空比相同，即Vi1=Vi2、Ds1=Ds2=D，则增益表达式为

(6)

2.1.2 电源Vi1单独供电情况

根据式(1)～式(3)可以得到此模式下输出电压为

(7)

增益为

(8)

2.1.3 电源Vi2单独供电情况

对电感L2，根据伏秒平衡式有

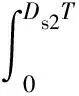
(9)

稳态下有Vc2=Vi2，可以得到输出电压

(10)

增益为

(11)

假设两路输入电压相同，占空比相同，可以绘出本拓扑在双输入、单输入情况下电压增益曲线，如图8所示。可以看出，在3种供电模式中，双路供电时变换器电压增益最高，Vi1单独供电时电压增益高于Vi2单独供电时电压增益。

图8 电压增益曲线

2.2 器件应力分析

由以上的各个工作模态及理论分析，可以推到得到各个开关器件在不同供电模式下的电压应力。

2.2.1Vi1单独供电

此模式下，开关管S1的电压应力为电容C1上的电压，开关管S2不承受电压，即

(12)

二极管D1、D3的电压应力为电容C2上电压，二极管D2的电压应力为电容C1上电压，由于2个电容电压相等，所以有：

(13)

2.2.2Vi2单独供电

此模式下，开关管S2的最大电压为输出电压减去电容C2上的电压，开关管S1在此模式下不承受电压，即

(14)

在二极管D4导通时，二极管D1承受最大电压，即输出电压减去电容C1上的电压，而电容C1上的电压为零，所以D1电压应力为Vo；同理，二极管D3导通时，二极管D4承受最大电压，二极管D2、D4导通时，二极管D3承受最大电压；二极管D2在此模式下不承受反压，具体应力为

(15)

2.2.3Vi1和Vi2同时供电

在双输入模式下，开关管S1的电压应力为电容C1上的电压，开关管S2在电感L2续流时承受最大电压，即输出电压减去电容C1、C2上的电压，具体表达式为：

(16)

在开关管S1导通时，二极管D2承受最大电压，即电容C1电压；同理，二极管D2导通时D4承受最大电压，二极管D4导通时D1承受最大电压；二极管D3在开关管S2断开时承受最大电压，具体表达式如下：

(17)

由以上推导可知，所提变换器具有较低的开关器件电压应力，在电路工作时半导体两端低的电压有助于降低电路损耗。

在电路设计时，应当按照最坏的应力条件进行器件选型。根据以上应力分析可以得到开关器件最大电压应力为

(18)

2.3 电路电流情况分析

假设Vi2路驱动信号相对于Vi1路驱动信号的相移为α，以开关管S1导通时刻为起点，之后的一个开关周期内，电感电流iL1为：

(19)

电感电流iL2为：

(20)

式(19)和式(20)中，电感电流iL1，iL2也为两路输入电流；IL1，IL2为电感电流平均值。

对于电容C1可以列写安秒平衡式：

(21)

化简后可得输入电流之间的关系：

(22)

可见，两路输入电流的比值仅与两路开关管的占空比有关，因此可以通过调节两路占空比的大小控制输入电流，进而对两路输入源进行功率分配与能量管理。两路输入源的功率关系可以由两路输入电压和式(22)得到，即

(23)

在实际闭环系统中，3种供电模式的开关管控制方式如下：双路供电时，输出端稳压是通过控制其中一个开关管(S1或S2)的占空比来实现，另一个开关管(S2或S1)的占空比是根据两路输入功率的比例及输入电压大小由式(23)得到，两路输入功率的比例分配由2个供电模块的功率大小确定，这样通过控制两路开关管的占空比就可以实现输出电压恒定及使两路输入功率按所设定的比例进行分配；Vi1单路供电时，输出端稳压是通过调节开关管S1的占空比实现(开关管S2始终保持开通)；Vi2单路供电时，输出端稳压是通过调节开关管S2的占空比实现(开关管S1始终保持关断)。

2.4 电感电容参数设计

为了保证电路工作于电感电流连续模式，电感取值须大于临界导通模式下的计算值，即

(24)

式中ΔiL1、ΔiL2分别为设计要求电感L1、L2电流的最大纹波值。

电容的取值主要考虑控制其电压纹波不超过设计限制值，其计算公式如下：

(25)

式中：ΔVC1、ΔVC2、ΔVo分别为电容C1、C2、Co可接受的最大电压纹波值；Io为输出电流平均值。

2.5 同类拓扑主要特性比较

为更好了解所提变换器性能，将之与同类的变换器拓扑进行了对比，具体数据如表1所示。为确保可比性，文献[16]变换器选取2个输入源的情况，文献[17]选取2个输入源和2个增压单元情况，所有变换器的各输入源电压相等，各主开关管占空比相等均为D。因部分拓扑无法实现单路供电的功能，所以开关管应力和电压增益均选取双输入时的情况进行比较。

表1 同类拓扑对比

可以看出，所提变换器的电压增益相比于双BOOST并联变换器、文献[17-18]变换器具有明显的优势，文献[16]在实现双输入的功能时使用了大量的开关管和电感电容器件，实现了高的电压增益，但是电路的成本较高，设计与控制比较复杂。本变换器在仅使用2个开关管和相对不多的无源器件时，实现了单输入源可独立供电的功能，确保了供电系统的可靠性；同时2个开关管共地，简化了驱动电路的设计；开关管应力较低，有助于器件选型和提高变换器的效率。

3 仿真与实验

3.1 仿真验证

为验证上述理论分析的正确性，本文对上述3种供电模式进行了仿真验证，并针对双路供电模式进行了输出短路和输入欠压的故障模拟仿真。仿真参数见表2，仿真结果如图9至图12所示。从图9至图11可以看出，双路供电时Ds1=Ds2=0.621、Vi1单路供电时Ds1=0.746，Vi2单路供电时Ds2=0.852，开关管的工作占空比与理论计算相符，且3种模式供电下输出电压均能稳定在380 V左右，各开关管、二极管以及电容的电压应力与理论分析一致。从图12可以看出，当发生短路和欠压故障时，2个开关管均关断，电路可以进行有效地保护，当故障消失后，电路又能恢复正常工作。

表2 电路仿真参数

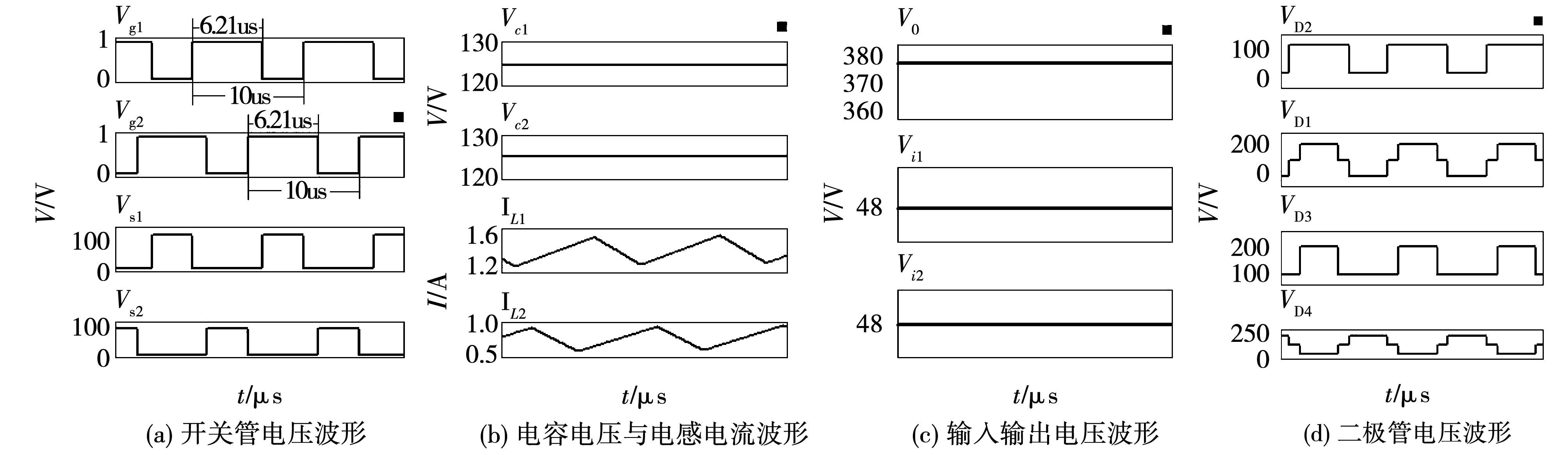
图9 双路供电仿真波形

图10 Vi1供电仿真波形

图11 Vi2供电仿真波形

图12 故障仿真波形

3.2 实验验证

基于上述分析，搭建了一台双输入高增益DC-DC变换器样机。表3所示为实验条件以及根据式(18)、式(24)、式(25)确定的元件参数和型号。实验平台如图13所示。

图13 实验平台

表3 电路参数

图14为Vi1=Vi2=48 V时的实验波形。其中图14(a)为2个开关管的驱动电压ug1、ug2和漏源电压uds1、uds2波形，可以看出，电路工作在所设计的输入输出电压时，2个开关管工作占空比为Ds1=Ds2=0.623，可以在实现较高增益的同时避免了极大占空比的出现，2个开关管漏源电压的最大值分别为127.9 V、128.4 V；图14(b)为Vi1路和Vi2路的输入电流iin1，iin2以及电容C1、C2两端电压波形，稳态下输入电流连续，电容电压基本不变；图14(c)为两路输入源电压Vi1，Vi2与输出电压Vo波形，可以看出输出电压稳定在382.2 V；图14(d)为4个二极管两端电压，D1、D2、D3、D4的电压应力分别为255.3、128.1、207.5、254.6 V，与式(17)分析一致。

图14 双路供电实验波形

图15为Vi1路输入源单独供电且Vi1=48 V时的实验波形。其中图15(a)为2个开关管的漏源电压、Vi1路输入电流iin1以及开关管S1驱动电压波形，可以看出，Ds1=0.749，输入电流连续，开关管S1漏源电压最大值为192.5 V；图15(b)为输出电压和电容C1、C2两端电压波形，C1、C2电压基本不变，输出电压稳定在381.6 V；图15(c)为4个二极管两端电压，D1、D2、D3、D4的电压应力分别为192.2、191.9、192.7、193.1 V，约为输出电压一半，与式(13)分析一致。

图15 Vi1供电实验波形

图16为Vi2路输入源单独供电且Vi2=48 V时的实验波形。其中图16(a)为2个开关管的漏源电压、Vi2路输入电流iin2以及开关管S2驱动电压波形，在开关管S2导通期间输入源会直接对电容C2充电，因此输入电流不是线性变化，开关管S2驱动占空比Ds2=0.857，开关管S2漏源电压为334.2 V；图16(b)为输出电压和电容C1、C2两端电压波形，C1、C2电压基本不变，输出电压稳定在382.4 V；图16(c)为4个二极管两端电压，D1、D2、D3、D4的电压应力分别为383.4、0、334.6、333.9 V，与式(15)分析一致。

图17给出了变换器在不同输入电压时的实验波形。其中，图17(a)、图17(b)为双路供电时不同输入电压的波形，可以看出两路输入电压变化时2个开关管占空比随之变化，而输出电压保持不变；图17(c)、图17(d)为单路供电时的工作波形，结合图15(a)、图16(a)可以看出，输入电压变化时，通过改变占空比仍可使输出电压保持不变。不同输入条件下电压增益与占空比关系均与理论分析相符。

图16 Vi2供电实验波形

图17 不同输入电压实验波形

表4为在满载条件下，不同输入电压时测得的变换器效率数据。

表4 效率数据

图18为在额定输入条件、不同供电模式下变换器效率随输出功率变化的曲线，样机在双路输入时满载效率为96.10%，Vi1单独供电时满载效率为94.79%，Vi2单独供电时满载效率为93.71%。在3种供电模式中，双路供电时电压增益最高、开关器件电压应力最低，效率最高。

图18 效率曲线

4 结 论

本文提出了一种基于开关电容增压单元的双输入高增益DC/DC变换器，通过实验验证了该拓扑的可行性。本拓扑具备以下优点：

1)具备双输入的功能，既可以在双路输入电源同时供电下工作，也可以在任意一路输入电源单独供电下工作，提高了电路供电灵活性。

2)电路具有较高的电压增益，能够有效地避免开关管工作在极限占空比状态，同时降低开关器件的电流应力。

3)3种供电方式下，开关管和二极管的电压应力均得到降低。因此可以选择较低电压等级的开关器件，有利于降低电路成本，减少开关损耗，提高变换器效率。