面向编队卫星的空间系绳在轨服务

严 冰,张 进,罗亚中

(国防科技大学空天科学学院,湖南 长沙 410073)

0 引 言

随着航天科技的发展,原来由单颗大型卫星完成的任务,越来越多地被多个集群编队小卫星完成。针对数目众多的卫星集群的修理维护、推进剂加注等将具有越来越广泛的需求。编队卫星作为一类特殊的卫星集群,其相对运动轨迹围绕参考卫星成特殊构型,包括直线构型、平面圆构型、空间圆构型等[1]。面向编队卫星的在轨服务模式需要基于其相对运动构型的特点开展。

绳系卫星系统(tethered satellite system,TSS)自20世纪提出以来,一直受到研究人员的持续关注。由于其具有长基线、可变构型等特点,在产生人工重力[2]、轨道转移[3]、空间碎片离轨[4]、在轨服务[5]等方面具有重要的应用价值。绳系系统的难点在于其动力学十分复杂,而且系绳的留位和回收运动较难稳定[6-7]。特别地,当系绳在松弛和绷紧两种状态之间来回切换时,极易引发系绳的振荡,对所执行的任务带来隐患[8],为此需要采取有效的主动控制方法。已有的研究方案主要分为绳长速率控制、拉力控制和辅助外力控制[9],辅助外力控制又分为电动力控制和推力控制。Yu[10]等提出了一种绳长速率控制方法,发现了一些具有特殊价值的特定运动形态(如平衡状态),这对解决TSS的稳定控制有着指导意义。此外，最优控制和滑模控制被广泛应用于系绳的拉力控制。最优控制通常设计一个目标函数,基于伪谱法[11]或者滚动时域控制[12]来优化系绳的拉力,以在充分考虑系统实际约束的条件下满足目标函数。Fujii[13]等和Kokubun[14]等将系绳展开和回收的过程转化为两点边值问题,基于滚动时域控制设计了系绳的最佳路径,并根据李雅普诺夫函数设计出一个状态反馈控制器,减小实际轨迹与最佳路径的偏差。Williams[15]分别推导了杆模型和珠点模型下球坐标系的状态微分方程,并针对珠点模型采用进化算法最小化系绳长度的二阶导数,来控制系绳的运动。滑模控制由于其强鲁棒性能较好,在近十年逐渐应用于系绳控制。常见的滑模控制包含自适应滑模控制[16]、分层滑模控制[17]、终端滑模控制[18]等,可以有效抑制系绳的振荡和干扰,Wang[19]等人还结合李雅普诺夫函数验证了有限时间TSS的稳定性。随着绳系卫星应用的快速发展,具备机动能力的TSS成为研究热点。通过系绳一端的主卫星施加推力,结合拉力控制,能够很好地保证系绳展开、留位和回收运动的有效性。Sun[20]等人则研究了轨道平面内具有化学推进能力的TSS的稳定性和控制方法。在假设推力恒定时,采用分层滑模拉力控制来追踪期望的面内角。Li[21]等人对系绳控制碎片离轨进行了研究,在假设系绳长度不变的情况下,提出了离线开环控制优化和在线闭环控制优化方法。Razzaghi[22]等人在研究系绳-卫星-碎片系统时,分别采用滑模控制(slide mode control,SMC)和状态独立的黎卡提方程(state dependent Riccati equation,SDRE)来求解系统的控制和稳定问题。仿真结果表明,SMC的各方面表现均优于SDRE。与推力控制不同的是,基于洛伦兹力的电动力系绳控制则充分利用了地球磁场,无需消耗推进剂[23],但在控制要求上要高于辅助推力控制。

TSS的一个重要特点就是改变两个航天器间的相对位置主要靠系绳拉力,不直接消耗或消耗很少推进剂。基于此,本文提出了一种基于绳系系统的多星在轨服务方案:小质量服务航天器与大质量燃料站通过系绳连接成服务系统,在服务多颗编队卫星时主要位置转移由小质量服务航天器完成,以节省推进剂。全文内容安排如下:第1节以编队卫星为服务对象,设计了由燃料站-系绳-服务航天器构成的TSS;第2节介绍了编队卫星和TSS的相对动力学模型;第3节综合考虑系绳释放过程和对接时刻的状态约束,基于Radau伪谱法设计了以推进剂消耗为指标的绳系最优控制策略;第4节通过两个仿真算例,对比分析了TSS以及单卫星平台服务不同数目的编队卫星所需要的燃耗,并讨论了TSS在轨服务的优缺点。

1 服务编队卫星的TSS设计

双体绳系系统中子航天器具有质量轻、体积小以及可重复利用等特点[24],根据动量守恒定理,靠近系统质心一端的主航天器只需小位移机动,便可使得远在另一端的子航天器在基本不消耗燃料的情况下完成长距离的位置转移。基于此，本文设计了服务航天器-系绳-燃料站模式的TSS,根据动量守恒定律燃料站相对TSS质心只作少量机动,而服务航天器可以转移至较远的编队卫星处。此外，为了加强燃料站和服务航天器之间的联系,系绳被设计成内部中空的管道,以便于在不改变服务航天器自身规模的情况下服务更多数目的编队卫星。

编队卫星的构型特点是所有伴飞卫星均围绕参考卫星(可以是个参考点)呈现一定规律的相对运动轨迹,如空间圆构型编队卫星的相对运动轨迹就是以参考卫星为圆心的空间圆。本文设计的TSS系统质心始终贴合参考卫星,其优势有两点:一是燃料站靠近质心,质心不动意味着燃料站的移动范围也较小；二是编队卫星的运动规律主要体现在其相对运动轨迹上,绳系质心固定在参考卫星,则可充分研究TSS 在以参考卫星为原点的相对坐标系下的运动过程,简化了绳系动力学的复杂度。具体服务流程可分为以下4个步骤。

步骤 1服务航天器从燃料站出发,牵引着一根内部灌满推进剂的系绳管道,施加有限推力与第一颗目标星交会;

步骤 2与目标星对接成功后,控制卷扬机使系绳拉力保持交会时刻的大小不变,调整服务航天器的推力大小和方向,使其与拉力为一对相互作用力,保证目标星的编队构型不被破坏,同时打开闸门进行加注,输送完毕后关闭闸门;

步骤 3服务航天器停泊片刻,根据给定的访问序列与下一颗目标星交会;

步骤 4重复步骤2和步骤3,直至服务完所有的目标星后,机动返回燃料站,从而完成一对多的在轨服务任务。

本文利用TSS解决编队卫星在轨服务的难点主要有两个。难点一是控制策略,由于TSS的动力学模型相对复杂,其控制策略需要考虑重力差与系绳拉力特点,而且系绳的状态变化需要保持在一定范围内以避免发生振荡。特别地,当服务航天器与编队卫星完成对接时,系绳的状态还有附加约束。基于此,本文基于伪谱法设计了含有过程与交会约束的绳系最优控制策略。伪谱法采用全局插值多项式来近似控制量和状态量,不需要推导一阶最优条件,还能在多约束情况下满足计算精度和结果的最优性,具有应用于实际系统实时最优控制的潜力[25]。除此之外,为了降低TSS的自由度,假设初始时刻燃料站和服务航天器位于编队卫星的参考卫星处,并且要求两个航天器施加的推力是一对相互作用力,由此TSS质心始终与参考卫星重合,仅需要研究系统相对质心的三维运动。另一个难点就是系绳管道的设计,本文将其设计成一个内部中空的管道,目的是要在不改变服务航天器规模的条件下满足不同编队数目的在轨服务要求,如图1所示。

图1 服务编队卫星的TSS示意图Fig.1 Diagram of TSS for service formation satellites

图1中,管道中间有层薄膜可将氧化剂和燃烧剂分隔开,但这对系绳的密封性和延展性提出了很高的要求,此外还要求在释放过程中管道内部始终灌满推进剂,使得系绳管道的质量变化仅与释放时间和长度有关。

2 动力学模型

2.1 编队飞行动力学

编队卫星分为参考卫星和环绕卫星,将编队卫星的运动投影到以参考卫星为原点的LVLH(local vertical local horizontal)坐标系O-xyz下,并有如下假设:

假设 1忽略任何摄动力和控制力;

假设 2参考卫星为近圆轨道;

假设 3绕飞卫星与参考卫星的距离远远小于后者的地心距;

假设 4xOy平面内的相对运动轨迹是一个以参考卫星(LVLH系原点)为中心的椭圆。

可得到编队飞行运动方程[1]的解析解为

(1)

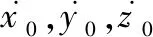
在考虑空间绕飞轨道为圆轨道时,应当满足x2+y2+z2=r2,则可得到编队为空间圆构型[26]的相对运动方程为

(2)

式中,r为绕飞半径;σ为绕飞卫星的相位角。σ1,σ2,…,σN的表达式为

(3)

2.2 系绳动力学

TSS的运动可分为三维的绳系质心运动以及三维的系绳自由振动。第2.1节中假设服务航天器和燃料站均施加有限推力,且为一对相互作用力,则有3个控制分量。初始时刻TSS位于编队卫星的参考卫星处,在二体条件下质心的绝对运动与编队卫星的参考卫星一致,自由度仅剩系绳相对质心的三维自由振动,大大简化了TSS的动力学特性。基于此,进行如下假设:

假设 5忽略任何摄动力;

假设 6系绳采用杆模型,忽略系绳的弹性、弯曲性和可伸展性;

假设 7两类航天器均视为质点,不考虑姿态运动;

假设 8TSS质心始终与编队卫星的参考卫星重合,只受到保守力作用。

在以质心为原点的LVLH系下用3个广义坐标描述系绳自由振动,分别是绳长l、面内角θ和面外角φ。定义绳长矢量l的正方向由燃料站指向服务航天器,则θ为l在xOy平面内的投影与x轴的夹角,φ为矢量l与此面内投影的夹角。参考文献[27],可得到TSS的拉格朗日方程为

记系绳受到的拉力大小为T,进一步可推导得出TSS关于l、θ和φ的微分方程组

(5)

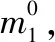
(6)

各部分质量关于时间t和绳长l的导数为

(7)

设航天器施加的有限推力矢量为F,记F在LVLH系下与z轴夹角的余角为φ,F在xOy平面内的投影与飞行方向y轴的夹角为ζ,则TSS所受广义力Ql、Qθ和Qφ的表达式为

(8)

式中,1表示燃料站;2表示服务航天器。以服务航天器的相对位置矢量方向为正方向,则li表达式为

(9)

基于假设4可知,当服务航天器和燃料站各自施加的推力互为相反力时,可满足TSS系统所受合外力为0。进而,式(8)可推导为Q=Ax的向量形式:

(10)

3 服务多星的绳系控制策略

为了确保绳系系统服务多星任务安全高效的开展,本文采取以TSS系统燃料消耗为指标的最优控制方法。通过电动卷扬机控制绳长提供拉力,服务航天器与燃料站的喷气发动机则提供推力。由式(5)和式(10)可知,TSS系统需要对系绳拉力大小T、两类航天器施加的推力大小F和方向φ、ζ进行控制,记控制输入为u=[T,F,ζ,φ]T。

目前较为成熟的最优控制软件包为GPOPS[28],本文采用其内置的Radau伪谱法来求解上述TSS的最优控制问题。由于TSS服务每颗编队卫星的约束条件与控制目标是相同的,服务航天器只需将上一颗编队卫星在LVLH系下的相对状态投影到在l、θ和φ方向,作为服务下一颗星的初始状态即可。下面给出绳系单次服务中各个模块的设计要求。

(1) 目标函数

针对多目标的绳系卫星在轨服务,其核心是要节约航天器的推进剂消耗,因此最优控制应当以最小化推进剂消耗为优化目标。记t0为初始时刻,tf为终端时刻,目标函数是拉格朗日积分型:

(11)

式中,Fmax为航天器最大推力值;u为表征实际推力大小的归一化变量;Isp为比冲;g0为海平面重力加速度。

(2) 初始和终端条件

(3) 过程约束

过程约束是指绳系卫星系统在执行任务时其状态量x和控制量u的上下界约束,则任意时刻下系统的状态量x(t)和控制量u(t)应满足

(12)

(4) 附加约束条件

当服务航天器与目标卫星进行交会对接,两类航天器在位置和速度上是重合的,对应的状态量x约束为

(13)

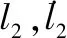
综上,对于n颗编队卫星的在轨服务任务,TSS的起始和终端状态都通过人为设计得出,中间的控制过程只需将上述流程循环n+1次即可,第n+1次的目标为LVLH系原点,即TSS回收服务航天器。

4 算例分析

针对空间圆构型的编队卫星在轨服务任务,本文以分别由3/4/5颗伴飞卫星组成的编队为服务对象,首先利用TSS进行在轨服务,通过仿真结果验证分析所建模型和方案的合理性。再采用单个大卫星平台对这3组编队卫星进行相同的在轨服务任务,并对两种方案的推进剂消耗进行对比。3组编队卫星的参考卫星相同,相位分布有所差异,具体参数如表1所示。

表1 编队卫星的参数设置Table 1 Parameters setting of formation satellites

4.1 TSS在轨服务

常见系绳直径约为0.05 cm[29],考虑到本文将系绳拓展成输送管道,若尺寸太小则无法满足在轨服务要求,太大又会导致系绳的质量增加,提高TSS空间操作的风险。基于此,本文选取外径为0.8 cm,内径为0.6 cm的管道。系绳材质选用强度高、质量轻的迪尼玛,其密度为0.99 g/cm3,液体推进剂由液氢和液氧构成,密度分别是0.071 g/cm3和1.149 g/cm3,则管道的折合密度为1.119 g/cm3。此外,收放系绳的机构采用电动卷扬机,系绳末端与轴面的导管相连,导管另一端则从转轴侧面延伸出来连通燃料储箱,系绳头部则与服务航天器相连,通过电机的转动实现系绳的收放。

针对目标半径为1 000 m的编队卫星,系绳总长lm设为1 200 m。相关常量设置如表2所示。

表2 TSS的参数设置Table 2 Parameters setting of TSS

初始和终端时刻服务航天器与燃料站位置均重合,且位于参考卫星原点附近,但当l=0时,动力学方程式(5)会出现奇异。初始长度和终端长度需要设为一个略大于0的常数。具体数值如表3所示。

表3 TSS的初始和终端状态Table 3 Initial and terminal state of TSS

在系统执行任务过程中,除了对状态进行约束外,还需要根据实际系绳材质与执行机构对控制输入进行约束。从安全角度考虑,系绳应该始终保持绷紧状态,避免绳子在松弛和绷紧两个状态来回切换时产生振荡,本文假设系绳在拉力始终大于0的条件下始终能够保持绷紧状态,则系统的状态和控制约束如表4所示。

表4 TSS的状态与控制约束Table 4 State and control constraints of TSS

表4中,系绳以及推力的面内角均在-π～π,而面外角在-π/2～π/2;绳长伸长率不超过5 m/s,角度变化率最高为0.1 rad/s;拉力上限设为5 N,推力上限则设为10 N。迪尼玛材料的弹性模量E=172 GPa,由胡克定律E=σ/ε可知,当系绳长度达到1 000 m时,系绳受到5 N的拉力所产生的正应力σ=F/S,弹性形变仅为3.305×10-4m,则忽略系绳弹性是合理的。

TSS服务编队卫星的仿真结果如图2～图4所示。图2展示了系统服务3/4/5颗数目的编队卫星所得到的质量曲线,当服务3颗卫星时,系统的剩余质量为1 043.29 kg,除去固定输送的54 kg推进剂,机动共消耗推进剂2.76 kg;服务4颗卫星时,剩余质量为1 024.99 kg,机动燃耗3.01 kg;服务5颗卫星时,剩余质量为1 006.02 kg,机动燃耗为3.98 kg。由此可以看出,服务卫星的数目越多,TSS机动所消耗的推进剂也就越多。图3为绳系系统在不同任务下所对应的状态变化曲线,不难发现系绳的长度最长接近1 150 m,超出了圆半径150 m,这是因为当服务航天器对接目标星时,为了保持质心位置不发生变化,燃料站也需要作一小部分机动。此外,系绳的面内角和面外角在任务过程中变化平缓,没有陡升或陡降,说明系绳发生振荡或缠绕的可能性较小。图4则为系统在对应任务中的控制曲线,其中拉力曲线在执行任务的过程中一直保持在最小值0.2 N附近,既能满足绳子拉直的假设条件,又能降低服务航天器与目标卫星对接时的燃耗;推力曲线则满足典型的bang-bang控制,进一步说明仿真控制的最优性。

图2 TSS服务3/4/5颗星的质量曲线Fig.2 Mass curve for serving 3/4/5 satellites of TSS

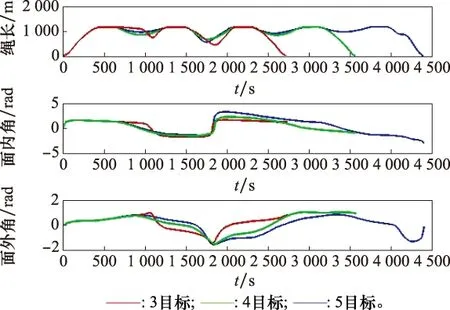
图3 TSS服务3/4/5颗星的状态曲线Fig.3 State curve for serving 3/4/5 satellites of TSS

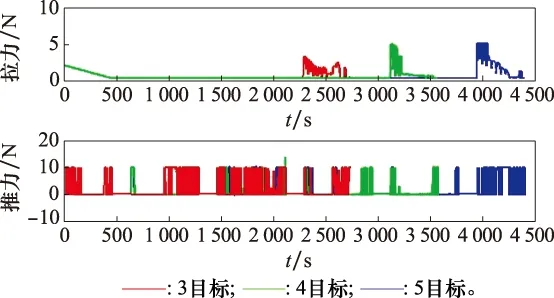
图4 TSS服务3/4/5颗星的控制曲线Fig.4 Control curve for serving 3/4/5 satellites of TSS

图5～图7分别展示了服务航天器与燃料站在服务3颗卫星时的位置、速度曲线以及三维轨迹。图5中服务航天器位于质心较远一侧,最远位移为1 000 m,最大速度为9.8 m/s,并且在任务终止时刻其位置和速度都收敛至0。图6中燃料站位于质心较近一侧,最远位移为150 m,最大速度为1.4 m/s,并且在任务终止时刻其位置和速度都收敛至0。从图7可以看出,初始时刻服务航天器从编队参考卫星处(LVLH系原点)出发,共对其4条相对轨迹进行最优控制,当航天器对接编队卫星后,两者的轨迹时刻保持一致,并在服务完所有目标星后,服务航天器成功返回原点,与燃料站完成对接。

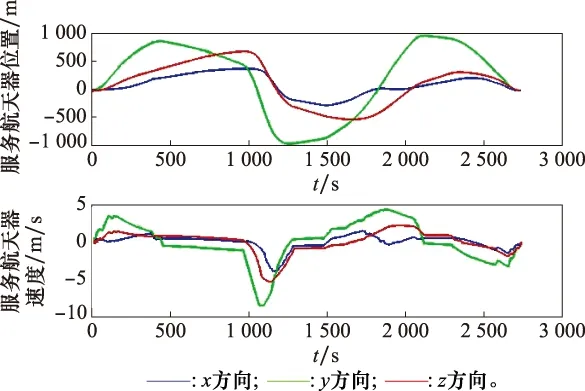
图5 面向3颗星的服务航天器位置和速度曲线Fig.5 Position and velocity curve of the service spacecraft for 3 satellites

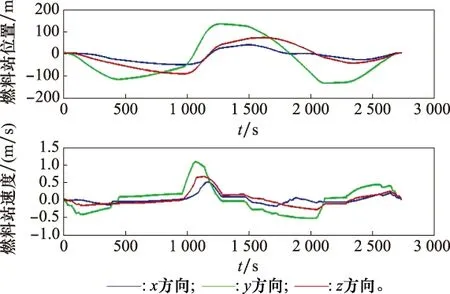
图6 面向3颗星的燃料站位置和速度曲线Fig.6 Position and velocity curve of the fuel station for 3 satellites

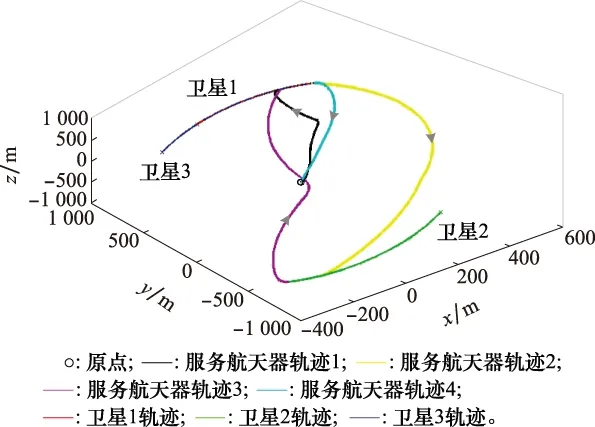
图7 服务航天器和编队卫星的相对运动轨迹Fig.7 Relative trajectory of service spacecraft and formation satellites

4.2 单卫星平台在轨服务

现有一个卫星平台,其初始质量和发动机推力水平均与绳系系统相当,令其与空间圆构型编队卫星依次进行交会对接,执行在轨服务的任务。初始时刻,卫星平台位于编队卫星的参考卫星处,动力学模型采用CW方程[30]。当平台与目标卫星对接成功后,卫星平台向编队卫星输送推进剂,此时发动机推力为0,保证编队构型不被破坏。当卫星平台服务完最后一颗编队卫星,即视为任务结束。

图8显示了单卫星平台服务3/4/5颗卫星的质量变化曲线,可以算出平台的推进剂消耗分别是5.06 kg、9 kg以及12 kg。由此可知卫星数目越多,卫星平台的燃耗也会逐渐增加。图9为平台的最优控制曲线,显然也满足bang-bang控制的特征。

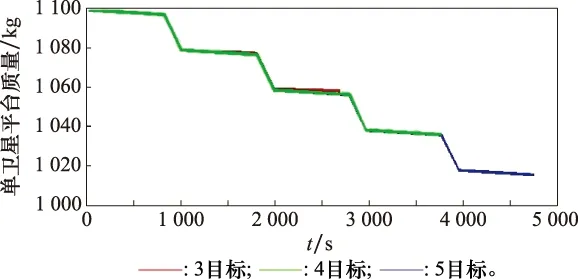
图8 单卫星平台服务3/4/5颗星的质量曲线Fig.8 Mass curve for serving 3/4/5 satellites of platform

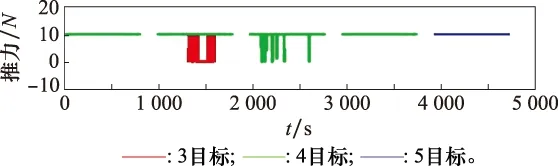
图9 单卫星平台服务3/4/5颗星的控制曲线Fig.9 Control curve for serving 3/4/5 satellites of platform

4.3 优势与不足讨论

从上述仿真结果来看,TSS能够很好地满足任务安全性所需要的约束条件,即系绳的状态变化平稳,绳长、面内角和面外角的变化率始终在一定范围内波动。仿真结果表明,使用TSS的优势有:

(1) 将系绳拓展成管道,在不增加服务航天器的推进剂质量的情况下,能够服务较多数目的编队卫星,且与单卫星平台相比,服务的卫星数目越多,节省的推进剂越多;

(2) 系绳的面积和质量增大,降低了绳子缠绕和振荡的风险。

表5 TSS和单卫星平台的燃耗对比Table 5 Comparison of fuel consumption between TSS and platform

不足之处有:

(1) 将系绳拓展成管道,对包裹在外围的系绳材质和设计提出了更高的要求,需要保证良好的密闭性和延展性;

(2) 目前得出的结论仅适用于圆构型的编队卫星,尚不具备普适性。

5 结 论

本文将TSS应用于编队卫星的在轨服务,首先设计了服务航天器-系绳-燃料站模式的TSS,系绳传输推进剂使得服务航天器可以面向不同数目的在轨服务任务,并给出了绳系动力学方程。然后以推进剂消耗最优为目标函数,结合绳系系统的状态与控制约束,设计了面向多星的最优控制策略。最后分别对TSS和单卫星平台服务3、4和5颗空间圆构型编队卫星的案例进行了仿真分析,两者的燃耗比由0.54降至0.33,这表明服务数目越多,TSS越节省推进剂。未来还可以考虑绳系质心位置有小范围波动、不同的空间圆半径以及其他编队构型等因素,更全面地研究TSS服务编队卫星的问题。