基于时空关联网络的机场机位运行过程建模
邢志伟,刘洪恩,李 彪,2,罗 谦,文 涛,陈肇欣
(1.中国民航大学电子信息与自动化学院,天津 300300;2.中国民航大学航空工程学院,天津 300300;3.中国民用航空局第二研究所,四川 成都 610041)
0 引 言
目前机场运行呈现出大型化和复杂化的趋势,航班的高密度运行成为常态,机位分配也成为影响现代机场运行效率的瓶颈。航班机位分配问题(flight gate assignment problem,FGAP)作为典型的多输入多输出问题是研究难点,如何对机位运行时空演化过程进行精确的定量描述是机位分配问题研究的前提和关键。
既有文献集中于规划模型[1-7]、强化学习模型[8]、因果模型[9-10]、网络流模型[11-15]、图模型[16-17]、网络模型[18-21]等。规划模型以最小化旅客行走距离、最小机位变动等为目标达到优化目的,以机位机型匹配等为约束满足机场实际需求,产生了线性规划模型[1]、整数规划模型[2-5]以及混合整数规划模型[6-7]。但此类方法在模型约束上有不同程度的简化失真,例如对机场运行过程中来自气象、管制等外界不可抗因素产生的影响考虑不足。强化学习模型[8]学习效果较好。为改进模型以适应延误等情况发生,文献[9]基于着色Petri网(colored Petri nets,CPN)建立的因果模型对于描述航班延误在机场运行中的影响传播以及应对延误的恢复策略表现较好。但处于连续变化的航班时刻表使得运行必须对时间窗作动态调整,以逻辑相对固定的库所、变迁为动作的Petri网适用性相对不足。网络流模型[11-12]可以灵活地描述航班机位变动,在考虑气象、航班变动等影响时适用于再分配问题,并且通过控制流向可以精确描述机位约束。在此基础上,文献[13-15]加入混合整数规划到网络流模型中,以期同时应对优化和再分配问题达到良好效果。但已有研究的问题场景主要为换乘旅客或机位与登机口的再分配,对国内机场存在的机位地理情况复杂、影响因素交叉、决策条件模糊等问题分析甚少。文献[16-17]建立机位图模型并分别使用图着色和图分区方法以集团划分得到最小约束冲突,但模型在数据规模增加时依赖复杂求解算法支撑。文献[18-23]使用时空信息融合模型应用于航空运输、舰船航迹、铁路线路分配与自导车辆路由(automated guided vehicles,AGV)等问题,在运行过程刻画、优化问题建模与信息融合数据挖掘方面具有优越性。文献[24-27]以经典规划模型为主,研究聚焦于多目标优化、鲁棒性增强、算法求解速率及精确度等方面。文献[28-33]涉及到的模型改进多针对机位容量、旅客行走距离、机位运行时间均衡、航班时刻波动的吸收或其多目标综合等前设约束方面,并考虑了机位再分配的决策逻辑。与此同时,此类文献中机位的各类约束及求解目标对建模同样具有启发和指导意义。
综上,已有研究使用的模型在运行场景变更、数据规模增加以及突发情况下会产生约束条件失效模型失真等现象,未考虑航班与机位之间的关联,缺乏对宏观场景间差异的特征刻画,导致运行态势的辨别缺少支撑。以期对上述问题研究,基于复杂网络理论研究机场实际机位运行流程宏观及微观特征信息,参数化定量描述模型以及基于模型的特征信息规律分析方法,并使用历史数据驱动对模型的有效性进行验证。
1 基于时空网络的机位运行分析
在对机位运行流程分析研究的基础上,基于图结构的数据挖掘并加入复杂网络相关概念和分析手段,将离散化的机位运行对象抽象为关系关联表达和网络拓扑结构,并通过将对象特征进行网络属性化以实现量化分析。
1.1 机位运行流程
由飞行区、航站区和公共区构成的机场系统是现代综合交通系统中连接地侧和空侧的交通枢纽,如图1所示,机位相连着空侧飞行区与地测航站区,航空器在机位完成下次飞行前的停靠活动。

图1 机场运行功能分区示意图Fig.1 Schematic diagram of airport operation function partitioning
机位的使用是机场运行流程的重要环节,由机场调度或运行中心为到离港航班分配停机位资源,FGAP包括预分配和实时再分配。其中,机场预分配是指机场在前一天24点之前接收到次日各航空公司的航班计划后,根据当前机位的利用状况、停靠航班等信息,对机场机位进行预分配,并将机位分配计划传达到机场相关的保障部门。其余机场资源(如摆渡车辆、值机柜台、安检口、登机口等)需要参考机位计划进行预分配。
实际运行中呈现出多机位并行式的运行状态,结合网络化建模需要,机位运行过程时空关联网络建模主要为:以机位运行状态描述方法建立静态时空关联网络;以机位运行过程描述方法实现时空关联网络演化;以网络模型结构优化方法实现网络结构的非失真优化。
1.2 时空关联网络静态模型
以时空关联网络描述机位运行状态,V={v1,v2,…,vn}为网络节点,表示航班停靠到机位的逻辑关系存在,网络节点时间属性对应航班时刻,空间属性对应机位地理位置,网络节点的时空属性均使用相对坐标表示。空间属性为
(1)
式中,(xi,yi)为第i个机位的绝对坐标,其中i=0,1,…,n,n为机位总量;(x0,y0)为空间零点(初位置)。绝对坐标是在机场建设阶段确定的,仅当机场布局变更或运行调整等特殊情况下变化。时间属性为
(2)

(3)
节点的时空属性可表示为
CG=[IF·SIF·T]
(4)

(5)
网络边E={e11,e12,…,e1n,…,en n}存在于任意两节点间,也称作弧,表示任意两航班间均存在时间空间关系,由此可得到n×n维的边集合可表示为
(6)
边的权重W={w11,w12,…,w1n,…,wn n},描述节点在时空属性上的关联及差异性,以欧氏距离表示对应的边权重为
(7)
式中,
(8)
(9)
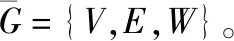
建立节点位置仿照地理上指状航站楼外围机位排布的全连接5节点网络图,如图2所示。

图2 仿地理位置排布的全连接5节点静态网络图Fig.2 Fully connected five-node static network diagram of imitating geographical location
在将地理位置数据加入网络模型的基础上,将仿地理位置排布转化为纵向排布,上述的5节点全连接网络模型等效为如图3的纵向形式。

图3 纵向排布的全连接5节点静态网络等效图Fig.3 Equivalent diagram of vertically arranged fully connected five-node static network
1.3 时空关联网络动态演化模型
由于网络模型中节点会随着时间t的推移,节点属性变量CG包含的时间属性T会随之变化,并且逻辑变量IF也存在变化的可能,从而进一步影响网络中节点的数量和属性,同时网络结构发生演化。

(10)
以白色节点图示存在节点,黑色节点图示消失节点。网络节点的变化根本上来自于t的变化,网络演化的来源即是节点的生成与消失。而通过上述的假设可以找出节点变化的时间,以此网络演化模型可表示为一系列的网络及其连接。依据不同的时间零点T0定义不同阶段,相邻的时间零点表示相邻的阶段,并于节点外侧设置节点、阶段指示符,变化过程如图4所示。

图4 相邻阶段的5节点网络离散图Fig.4 Discrete diagram of five-node network in adjacent stages
其中,阶段由时间零点定义,由零点集合中每一个时间零点表示,例如:节点4和节点5从第j阶段变化到第j+1阶段的触发条件为
(11)
并且可以得到网络演化的相邻节点集合:

(12)
式中,VP={v1,v2,…,vn1}表示网络演化中阶段较早的节点集;VL={v1,v2,…,vn2}表示网络演化中阶段较晚的节点集。
如图4所示,相邻两阶段中j表示相邻的较早阶段;j+1表示相邻的较晚阶段;i=4处节点的消失表示4号机位处航班于j+1阶段出港;i=5处节点的生成表示5号机位处航班于j+1阶段进港。以阶段更迭表示网络演化的细分。
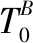

图5 两阶段的5节点网络演化图Fig.5 Evolation diagram of two stage five-node network

图6 5阶段的5节点时空关联网络演化模型Fig.6 Evolution model of five-node ralational spatio-temporal network with five stages
完整网络演化模型包括19个节点、27条内边和12条外边,可以证明在最复杂情况下,当数据维度增加时边的数量以指数增加,在保证信息不丢失前提下对模型的非失真优化是必须的。
1.4 时空关联网络优化
网络模型优化需保证网络中关联关系和信息不受影响,网络关联关系不变即节点与边存在逻辑,也就是网络主要结构不变;在网络主要结构不变的前提下,网络信息不变即是保证节点时空属性和节点连边权重不变。
模型节点由节点存在性性质决定,而边一方面取决于节点的存在,另一方面取决于节点的时间属性。内边的存在依赖于同阶段节点的存在,外边的存在依赖于不同阶段节点的存在,通过节点的时间属性确定而将所有外边简化为无向边。
若两个相邻阶段的节点完全相同,则将相邻阶段的节点合并删除掉外边,只需注意决定节点存在的生成时间零点和消失时间零点即可。边存在的实质是因为节点在时间维度上发生了交集,即节点有相同的时间属性,最后删除模型外侧的指示符完成优化。
图7为优化后的模型,只有7个节点和15条边,较之前简化了12个节点和24条边,并且消除了因外边存在带来的有向性问题。优化后的模型所拥有的15条边中有6条边是简化前模型中存在的,其余的9条边是经过内外边组合变化而得到的。例如,优化后的模型中,i=1第1阶段的节点与i=3第4阶段的节点之间的边,在意义上可看作是优化前模型中i=1第1阶段至第4阶段之间的3条外边和第4阶段i=1与i=3之间的1条内边合并得到。

图7 5阶段的5节点时空关联网络模型优化图Fig.7 Optimization diagram of five-node ralational spatio-temporal network with five stages
数据信息对应模型为:生成时间零点和消失时间零点分别为航班到港时间和离港时间,上述的优化操作是将描述同一航班到港离港节点合并为单一节点,使用机位的地理位置作为空间属性,使用实到实飞数据作为时间属性,属性信息合并而没有变动或缺失,优化操作可行。
2 机位运行特征参数化模型
在时空关联网络建立的基础上,加入多维度的网络特征,以多种定量参数指标进一步提高模型对场景描述的精确性。
2.1 机位运行特征
机场运行过程中呈现不同的应用场景和模态特征,航班密度随时间推移呈现一定的周期变化、高峰时段进出港航班量增加、气象和航空管制等不确定因素导致航班非正点情况。根据对象的描述层次将模态特征分为宏观特征(总体特征)和机位特征(微观特征),共同对运行过程做出参数化描述。
2.1.1 宏观特征
描述机场运行所需的宏观特征矩阵,包括在选定的时间段内的所有宏观特征参数:
UA={Δt,n,M,NA,HA,ρA,γA,RA,DA,AA}
(13)
式中,M为航班总量;NA为机位使用量;HA为高峰小时;ρA为航班密度;γA为航班正点率;RA为非正点情况;DA为航班延误率;AA为航班平均延误时间。
2.1.2 机位特征
机位特征是机位的所有微观特征参数集合:
UG={CG,BG,OG,RG,DG,AG}
(14)
式中,BG为机位繁忙程度;OG为机位使用率;RG为非正点原因;DG为机位延误率;AG为机位平均延误时间。
2.2 特征影响关系分析
系统实时运行中,由于不可控的随机因素(例如发生流量控制时采取的空中交通管制、恶劣天气、航空器机械故障等)常造成航班到达机位的时刻(航班到港上轮挡的时间)与计划时刻(航班时刻表上的时间)不一致,即航班的非正点情况。其中,提早到达情况可通过使航空器适当的盘旋飞行消除,而延误情况造成的波及程度相对较大,其影响消除更难。根据机场实施的《航班正常管理规定》并综合考虑机场标准间的差异及研究的需要,此处选定航班实际时刻比计划时刻延迟15 min以上或航班取消的情况称为延误。非正点情况的发生与机场运行效率和服务质量直接相关,尤其当航班发生延误传播情况影响剧烈,一般使用航班密度、机位使用率、延误率等参数衡量运行效率和运行质量。
图7的5节点网络模型中,由于i=1与i=2的节点度较高,处于运行的关键环节,在变更此航班的资源分配时会对邻居节点产生影响,即需同时考虑其余4个机位的是否随之调整。另一方面,集聚化高的网络中节点联系紧密,形成类似团或群体的局部聚集区域,区域内节点发生变化时对直接相连的相邻节点产生影响,但对区域外的不相邻节点影响较小。而集聚程度低的节点与相邻节点并未形成局部区域,更容易将此节点发生变化的影响传播到更广范围的节点。
图8为多级网络系统化建模方法流程,必要步骤包括模型层和信息层,即将机位运行的主要过程描述为网络模型,在此基础上加入节点和全局属性以及机位运行信息,对模型进行网络分布、航班动态信息、机位运行情况等方面的分析。
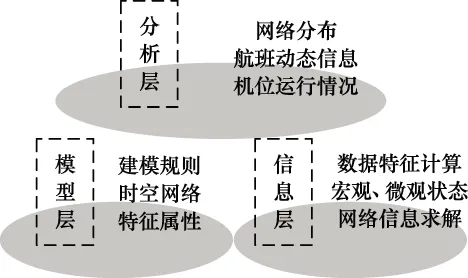
图8 建模方法Fig.8 Modeling method
3 基于数据驱动的时空关联网络模型
针对国内某机场实际运行数据建立时空网络模型,为突出模型对关联性较强的航班与机位运行的描述,选取呈现局部团状的机位运行数据进行分析,忽略局部之外的影响和其他次要影响因素,对机场单日(0:00-23:59)南方航空公司(编号为CZ)的运行数据过程建立时空网络模型。
3.1 运行数据预处理
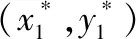

表1 经预处理后的机场机位运行数据Table 1 Preprocessed operation data of gates operation in airport

表2 机型对应参数Table 2 Corresponding parameter of aircraft type

表3 机位号对应参数Table 3 Corresponding parameter of aircraft tag number
3.2 数据驱动下的过程网络建模
预处理后的数据可驱动网络模型的行为、演化和模型分析,并可得到网络模型的机位特征和宏观特征所对应的节点属性和全局属性。依照方法步骤将相同航班实到、实飞的节点合并为单一节点,使用机位的地理位置作为空间属性,使用实到实飞数据作为时间属性T,以序号标注节点简化模型表示,并加入求取的其他宏观微观特征参数。模型的节点集、边集和模型度矩阵分别为
V={v1,v2,…,v31}
E={e11,e12,…,e3131}
D=diag(1,10,4,8,2,4,7,1,10,4,7,2,9,4,7,5,15,5,
13,13,17,12,18,21,12,12,13,12,16,19,13)
建立时空网络模型时将节点1和节点8剔除,以保证模型是连通图且分析可靠性较高,依据数据特征计算、状态及特征求解,得到如表4~表6所示时空网络模型的机位特征与宏观特征以及网络参数,图9为数据驱动的网络节点生成图,其中符号L表示当天结束时间为23:59。图10为优化后的时空关联网络模型。
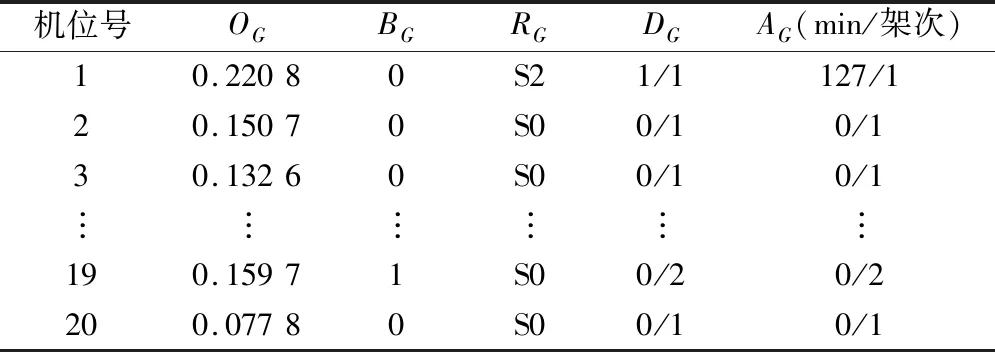
表4 机位特征表Table 4 Features of gates

表5 宏观特征Table 5 Macro characteristics

表6 网络参数Table 6 Network parameters

图9 数据驱动的网络节点生成图Fig.9 Generated diagram of date-driven network nodes

图10 实际数据驱动的时空关联网络模型Fig.10 Actual data-driven spatio-temporal relational network model
3.3 数据模型状态及特征分析
在确保网络连通的前提下,剔除对网络主体特征影响微小的局部节点,网络分析是对实际网络模型的子图开展。
如图11(a)所示,若用k表示节点的度,在相关系数R2=0.227 2时,拟合曲线为幂律分布P(k)=0.148k-0.421,整体趋势符合无标度网络的特点,即少数节点占据了整个网络中大部分连边,而多数节点的连边数量较少。如图11(b)所示,浅绿色节点表示度较低的节点,蓝色表示度较高的节点。

图11 网络模型节点度Fig.11 Node degree of network model
时空网络模型中,连边的存在表征了代表航班的节点之间有时间或空间上的交叉和冲突,其分布规律说明在机位运行过程中,少数航班对其他航班存在冲突影响,并有需要变更机位的潜在影响,而多数航班使用较少的机位资源并对其他航班影响较小,不发生共用机位的时空资源冲突。如图12(a)所示,在MAD=0.172 4时,聚类系数达到0.807 5。图12(b)中,绿色节点表示其聚类系数低于均值,黄色节点表示其聚类系数高于均值,红色节点表示其聚类系数为1。节点的聚类系数较高,说明航班与机位处于繁忙时空段,且此处发生变动或调整时对关联节点影响较大,需要综合考虑邻近的所有节点。宏观特征和机位特征存在关联,航班的高峰小时发生在网络连边密集的区段,58.62%聚集程度较高的节点对应的机位利用率和繁忙程度较高,结合航班信息可以发现,机场存在将繁忙航空公司的分配优先级提高或将隶属于相同航空公司的航班相邻分配的情况,邻近区域符合幂律分布和聚类系数较高的特点。区域分配是数据呈现的现象,可从系统网络分析发现此类模糊规律。

图12 网络模型聚类系数Fig.12 Clustering coefficient of network model
但实际数据驱动下的模型与标准无标度网络比较存在误差,原因主要有两点。一个是驱动数据为实际运行中随机影响因素与人工干预叠加作用后的再分配数据,数据内部包含了应对干扰的调整逻辑。另一个是驱动模型数据规模仅为机场单日局部机位群,存在系统性误差和随机性干扰,当数据的有效规模扩大时拟合精度改善。
3.4 模型对比与有效性验证
选取实际运行情况中具有代表性的弱、中、强3种不同规模复杂度的运行情况,其网络模型分别如图13和图14所示,节点数分别为17和58,与图10中29节点模型的节点度分布对比结果如图15所示,节点度分布幂律拟合如图16所示。
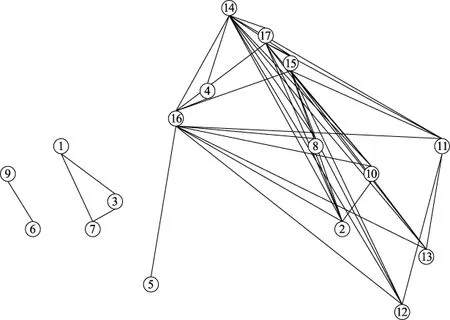
图13 小规模网络模型Fig.13 Small-scale network model

图14 大规模网络模型Fig.14 Large-scale network model

图15 不同规模网络节点度分布对比Fig.15 Comparison of node degree distribution in different scale networks

图16 不同规模网络节点度分布拟合Fig.16 Node degree distribution fitting of different scale networks
从图14的拟合效果可以看出,节点度分布在网络规模增大时精度有明显提升。通过对不同规模复杂度的网络对比分析可知,该模型适应于对不同规模的运行情况进行建模,对时空关联网络模型具有有效性。
4 结 论
本文分析了机场机位运行的规律,建立时空网络模型并提出基于时空网络仿真分析方法,得出以下结论。
(1) 较现有机位运行模型相比,网络模型基于航班进出港时间、机位地理信息等构成宏观和微观特征,提高了描述运行态势特征的准确性,并可灵活增删信息参数以满足运行的不同需要。运行过程中,航班与机位产生的关联随着数据规模变化,规模包含所选时间区间和所选机位容量以及特征多个维度,而时空网络模型可对时空关联进行精确的唯一描述。
(2) 设计了利用复杂网络理论对机位运行过程中机位及航班描述的网络分布分析的方法,可对大规模运行数据中航班延误、机位繁忙等情况作宏观微观分析。
(3) 网络模型与复杂网络理论对大规模数据的适应性,在历史数据的模糊规则挖掘方面具有优越性,可利用历史经验指导未来运行。在后续研究中需要引入更大规模的机位运行数据、干扰输入等因素,建立全机场机位运行网络模型,进一步研究在机场整体层面上的运行模式和信息特征。

