考虑荷载修正的衬砌背后空洞对结构安全性影响分析*
肖南润 丁祖德 刘正初 任志华
(1.昆明理工大学建筑工程学院 昆明 650500; 2.中铁二院昆明勘察设计研究院有限责任公司 昆明 650200; 3.云南省公路科学技术研究院 昆明 650513)
0 引言
随着我国西部大开发的进一步推进,大量基础设施建设进入了快速发展阶段。在隧道建设快速发展的同时,由于西部地质条件复杂,且受限于施工及监测技术水平,引发隧道缺陷,影响隧道的安全运营[1-2]。其中,衬砌背后空洞是我国山岭隧道最为常见的质量缺陷之一[3-4]。空洞会直接影响衬砌结构的受力状态,从而影响其承载力和安全性[5]。
国内外学者分别采用理论分析、数值计算和模型试验等方法进行了相关研究[6-13]。应国刚等[6]提出了一种荷载-结构模型的修正计算方法,确定了空洞临近范围内的围岩压力。MEGUID M A等[7]通过数值模拟,分析了衬砌背后空洞对围岩压力的影响,认为围岩压力在空洞临近范围随空洞尺寸的增大而增大。谢锋等[8]采用地层-结构法探讨了衬砌背后空洞存在时围岩压力的分布规律,并对荷载结构计算模型进行修正。在模型试验方面,方勇等[9]和佘健等[10]通过室内模型试验,对不同围岩、不同空洞位置以及不同地应力场条件下,衬砌的破坏形式、受力分布规律及承载力大小进行了研究。也有学者通过数值计算与模型试验相结合的方法,从空洞位置、空洞类型等方面,对衬砌结构承载力及安全性展开研究[11-13]。
现有研究加深了衬砌背后空洞对衬砌及围岩受力影响的认识,但考虑围岩压力修正,开展不同空洞位置与空洞范围下,衬砌安全性变化的研究较少。鉴于此,本文改进了空洞存在时的荷载修正计算方法,建立不同空洞位置、不同空洞范围条件下的衬砌结构内力计算模型,分析衬砌的内力分布特征及安全系数变化规律,为既有隧道衬砌结构安全性评价提供依据。
1 计算模型
1.1 工程背景
以云南省某公路隧道为背景,开展衬砌背后空洞对结构安全性影响的研究。隧道开挖断面宽12.24 m,高9.57 m。衬砌断面如图1所示。二次衬砌采用C30素混凝土衬砌,厚40 cm。隧道按深埋考虑,围岩级别为Ⅳ级,相关计算参数参照《公路隧道设计细则》[14]选取,具体见表1。

表1 计算模型材料参数
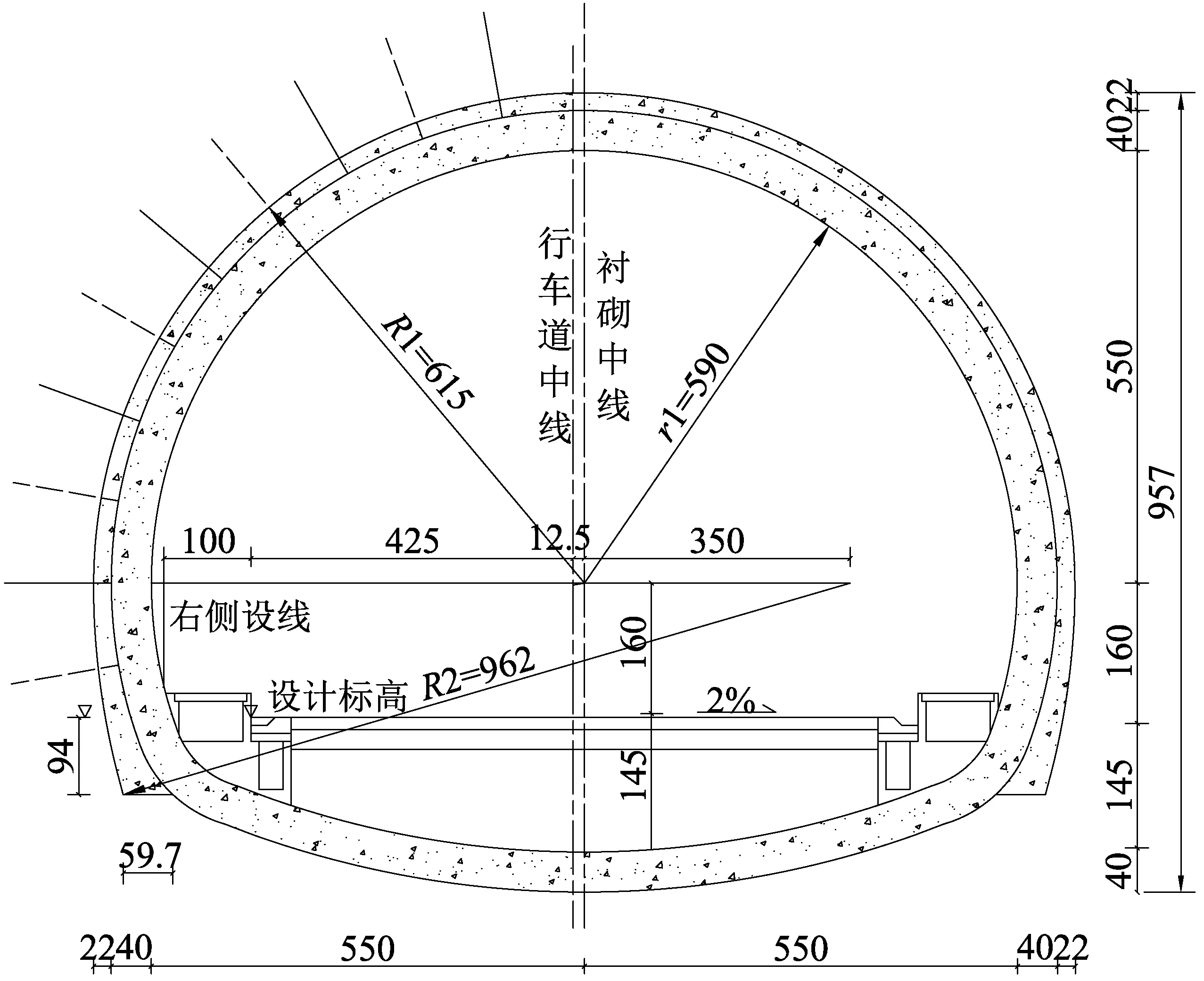
图1 隧道断面图(单位:mm)
1.2 围岩压力修正计算方法
依照规范计算得到隧道竖向围岩压力q=136.5 kN/m,水平向围岩压力e=54.4 kN/m,二次衬砌承载围岩荷载比例取30%[14]。采用荷载-结构法计算背后空洞对衬砌结构受力性能的影响时,围岩压力取值不能简单地去除空洞区荷载与约束,必须考虑空洞两侧的围岩压力集中效应[15]。应国刚等[6]提出了基于三角面积等效的围岩压力修正计算方法,但采用三角形面积等效,衬砌背后空洞较大时应力集中效应偏大,鉴于此,本文采用梯形面积等效方法,以改进围岩压力计算方法,如图2所示。
图中,r为空洞半径;q为无空洞时隧道上覆荷载;θ为空洞存在对围岩压力的影响范围与空洞半径之比;λ为围岩压力增大段与围岩压力影区域比例;qmax为压力峰值;B0表示最大开挖宽度的一半。
空洞影响范围一般为3r[6],最大影响范围为B0,根据空洞半径大小,有以下3种情况:
当r≤B0/4时,空洞区域荷载由空洞两侧衬砌承担。因此,图中两阴影面积相等:
S1=S2
(1)
(2)
S2=qr
(3)
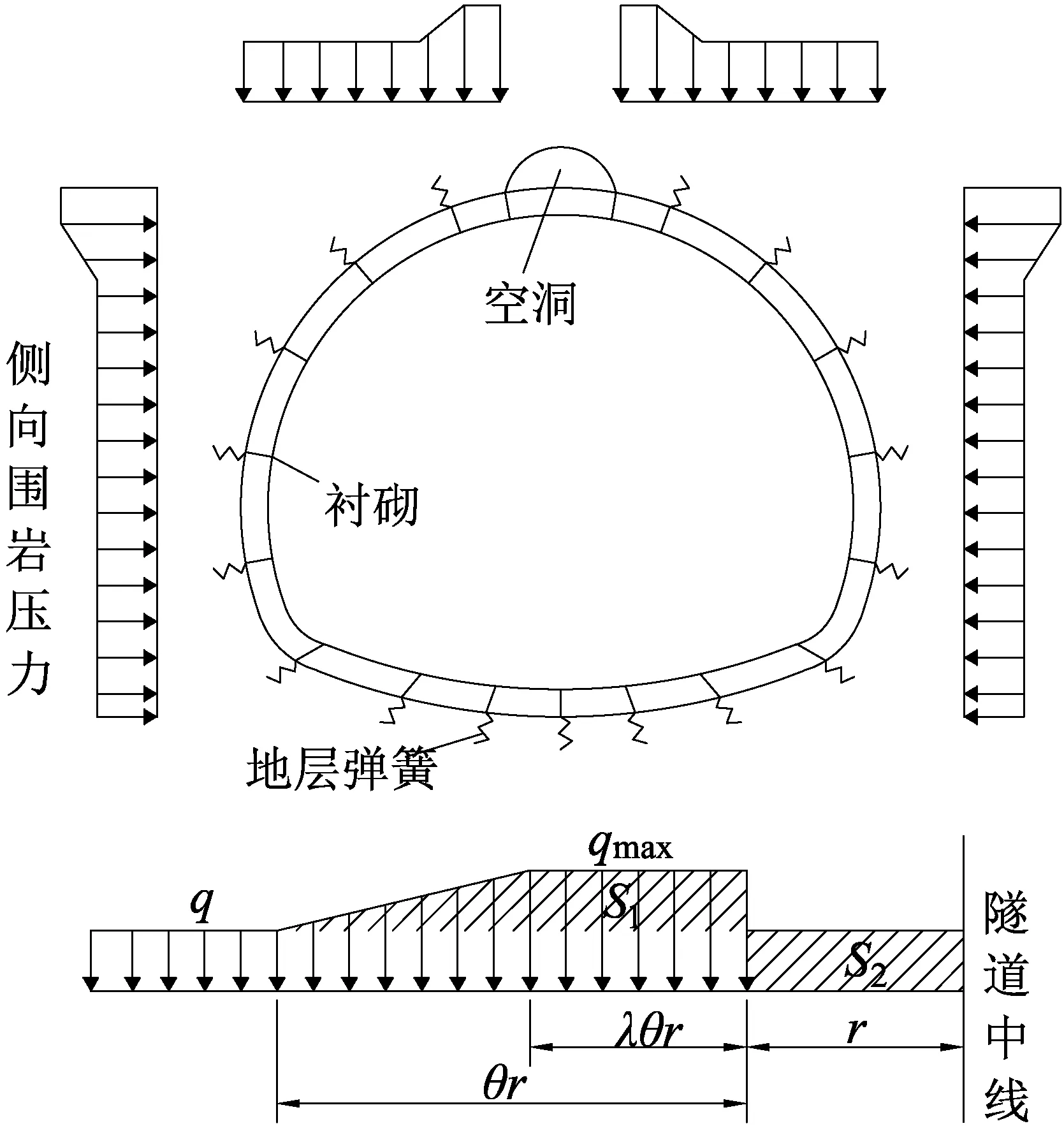
图2 空洞存在时的修正荷载-结构计算模型
当r>B0/4时,空洞影响范围到最大开挖宽度处,同理可知:
(4)
根据相关模型试验[6],空洞影响范围一般为3r,峰值靠近空洞边缘侧,位置约为1/3影响范围内,故θ和λ的取值分别为3和1/3。当r≥B0/2后,空洞影响区域变为矩形,综上可得qmax为:
(5)
确定隧道最大开挖宽度及空洞半径后,结合图2及式(5),计算可得空洞存在时的修正围岩压力。
1.3 计算工况
本次计算主要考虑空洞位置和空洞范围的影响,其中空洞位置取为拱顶空洞和左侧拱腰空洞,空洞范围α取15°至60°。图3为空洞缺陷示意,计算工况见表2。
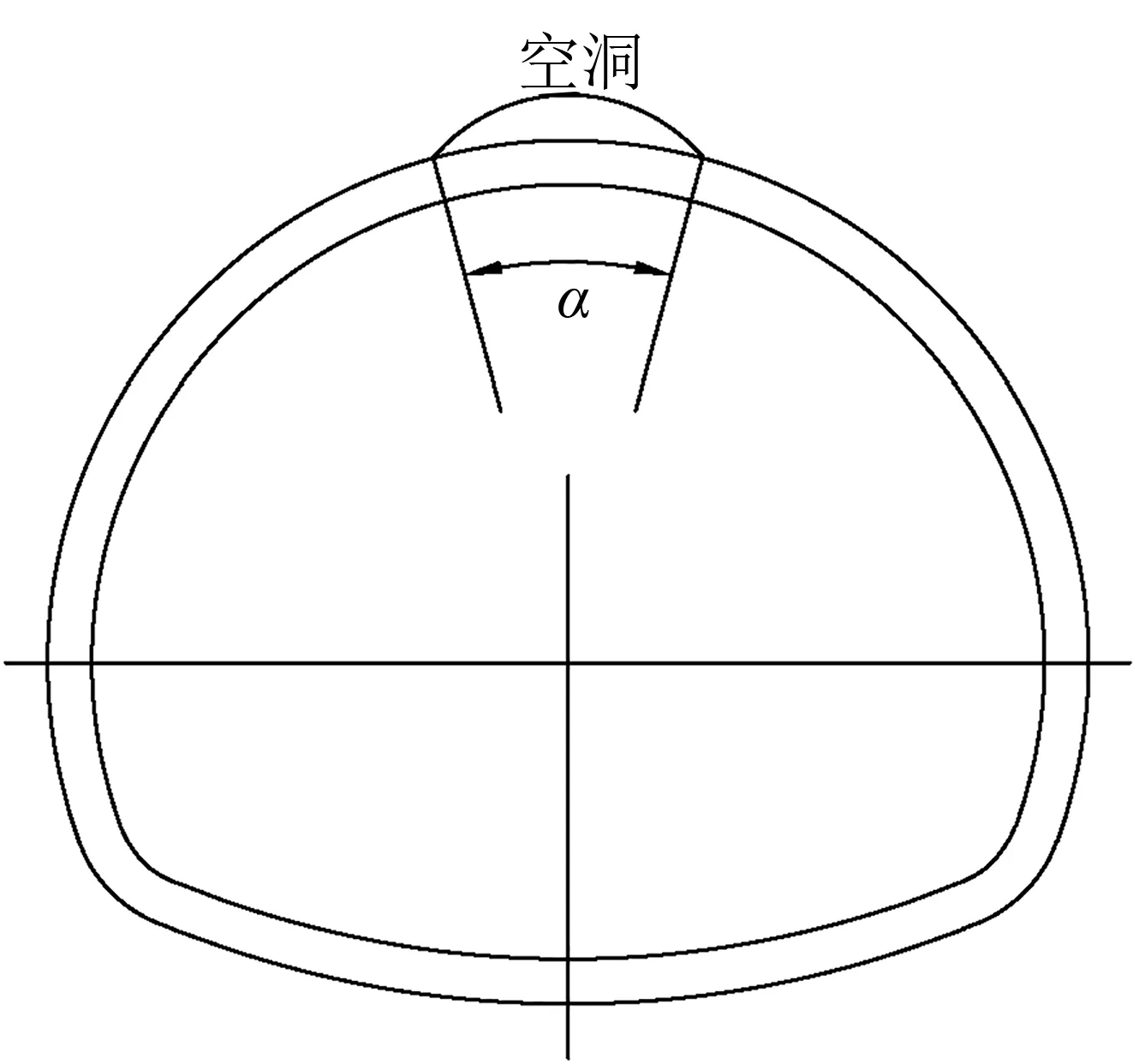
(a) 拱顶空洞
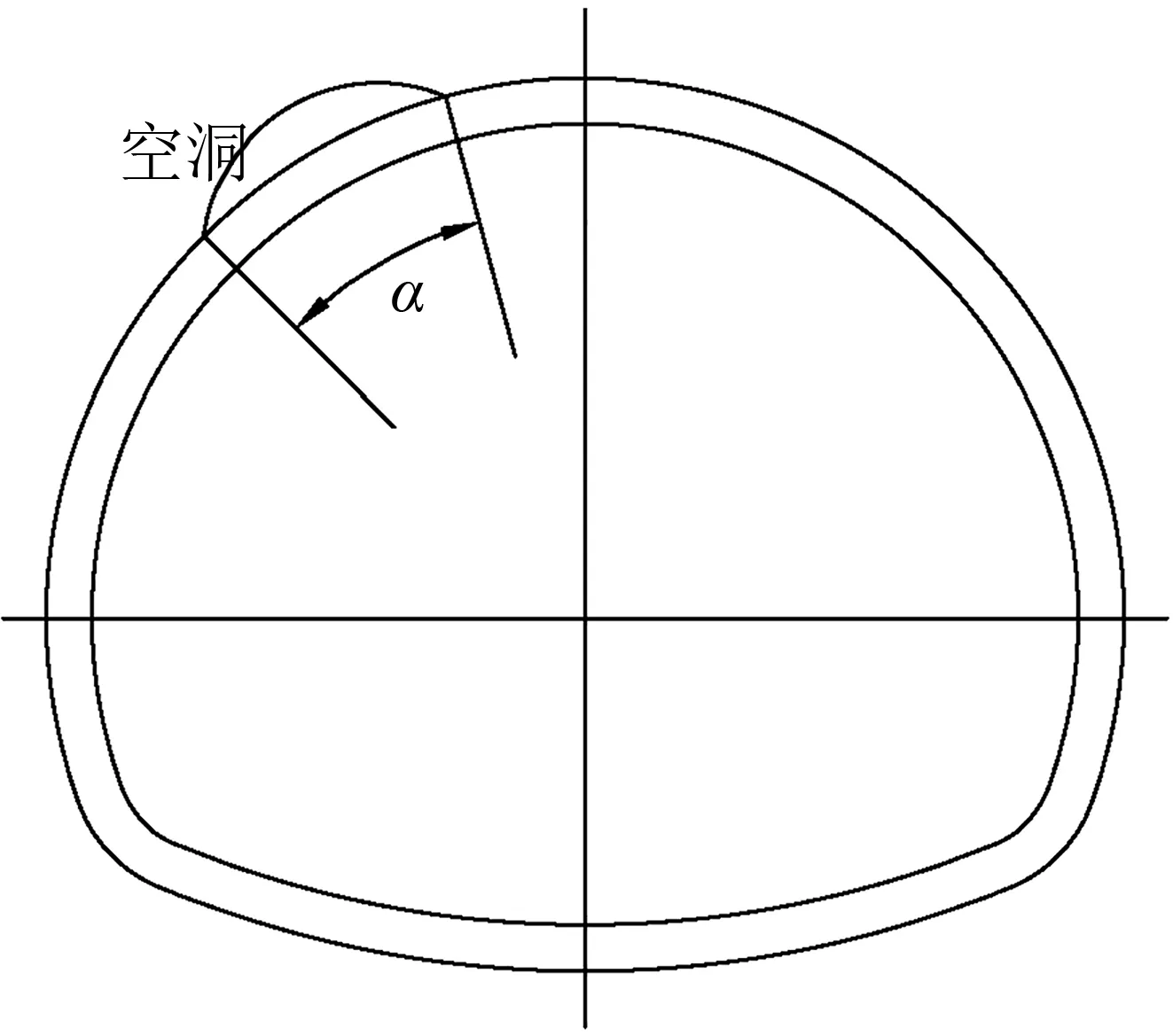
(b) 单侧拱腰空洞

表2 计算工况
1.4 衬砌安全性评价方法
衬砌截面安全系数K为衬砌极限承载力与其所受轴力之比[14]。根据衬砌所受偏心距不同,可分为两种情况:
(1)当偏心距e0≤0.2 h时,安全系数按抗压强度进行计算:
(6)
式中,Ra为混凝土的抗压极限强度;K为安全系数;N为轴力,kN;b为截面宽度,m;h为截面厚度,m;φ为构件纵向弯曲系数;α为轴向力的偏心影响系数。
(2)当偏心距e0>0.2 h时,由截面抗拉强度控制其承载能力,安全系数计算公式为:
(7)
式中,Rl为混凝土的抗拉极限强度;其他符号含义同前。
2 计算结果分析
2.1 轴力分析
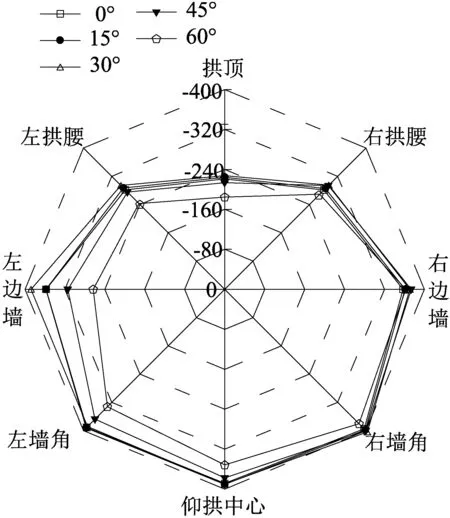
以衬砌空洞范围α=30°为例,计算得到衬砌的轴力分布云图如图4所示。衬砌轴力随着空洞范围变化的分布曲线见图5,轴力以受压为负。
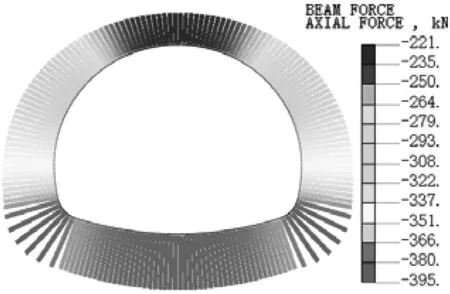
(a)完好衬砌
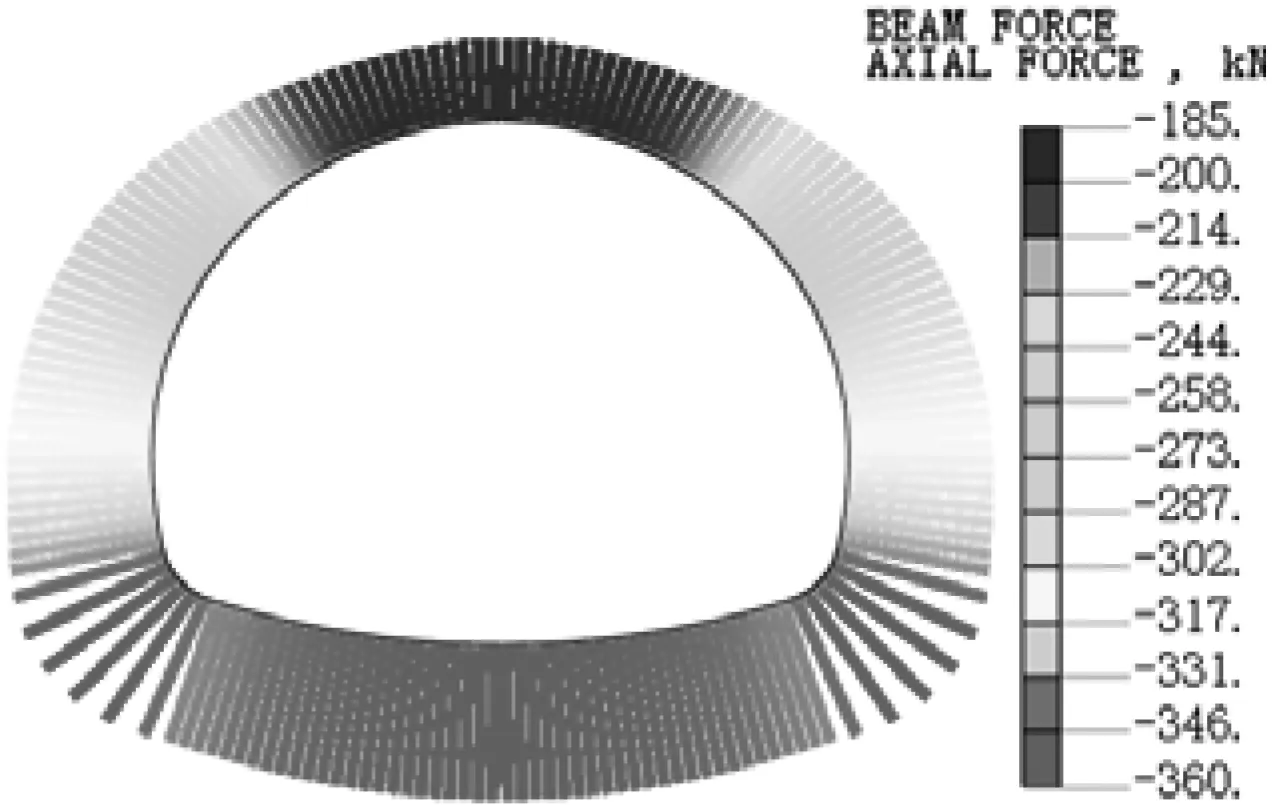
(b)拱顶空洞
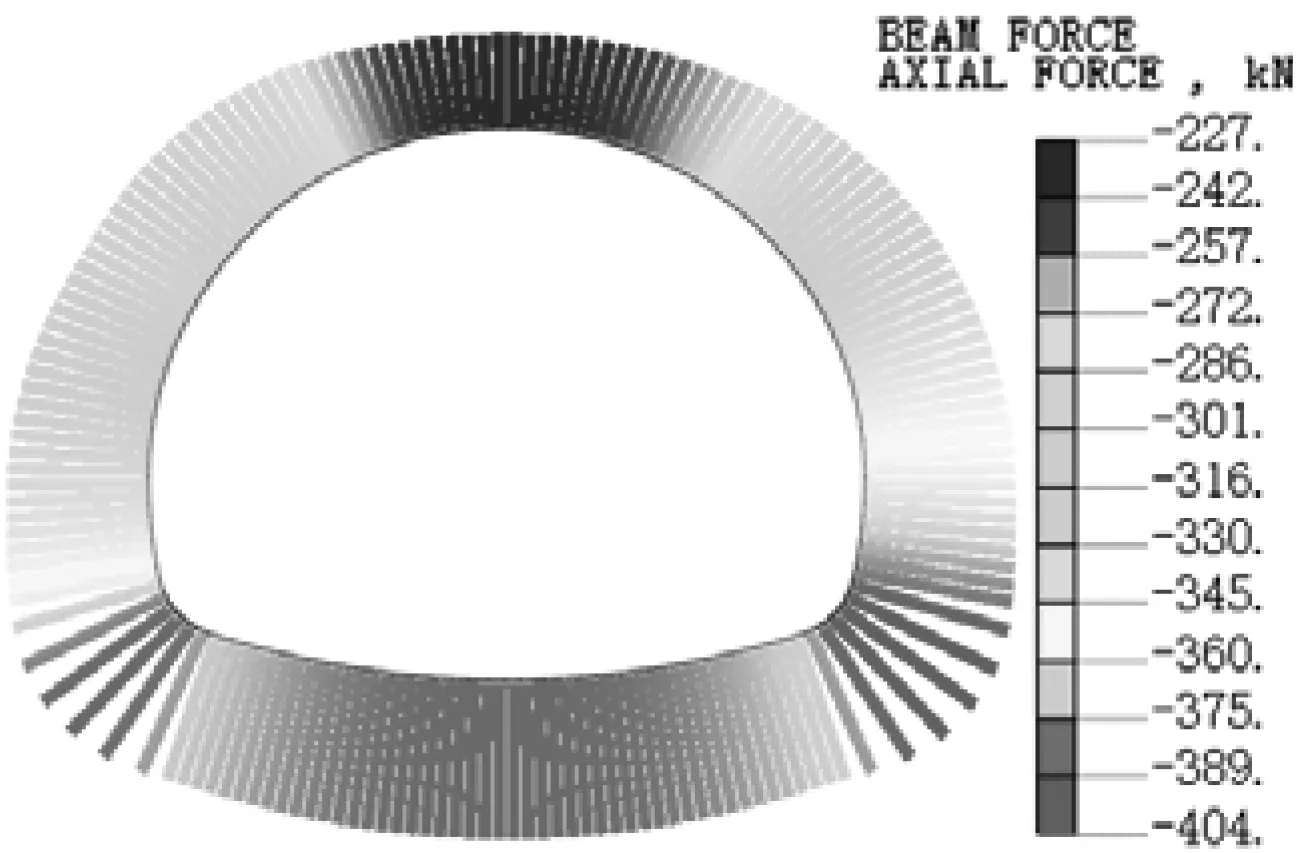
(c)左侧拱腰空洞
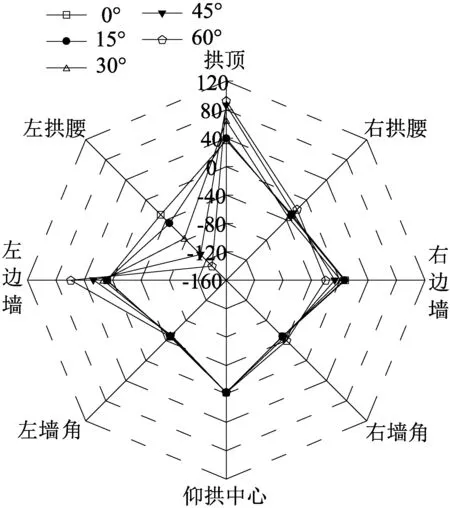
由图4可知,空洞出现位置不同,轴力分布形态基本一致,但空洞的出现引起衬砌轴力重分布,各典型部位轴力值差异明显。结合图5分析可知,随着空洞范围增大,空洞发生处,衬砌轴力明显降低,其余部位轴力变化较小。拱顶空洞角度从0°增大到60°时,拱顶轴力从-221 kN变化到-128.7 kN,减小了41.8%。当单侧拱腰存在空洞,空洞范围从0°增大到60°时,拱腰轴力从-281.6 kN变化到-242.9 kN,减小了13.7%。拱顶空洞对衬砌轴力的影响明显大于单侧拱腰空洞。
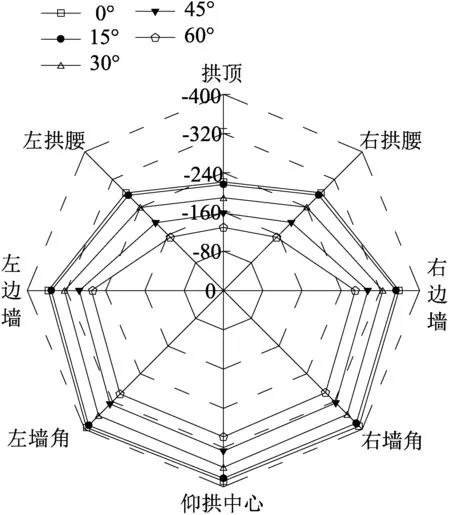
(a)拱顶空洞
(b)左侧拱腰空洞
2.2 弯矩分析
以衬砌空洞范围α=30°为例,计算得到衬砌的弯矩分布云图如图6所示,弯矩以结构内侧受拉为正。由图6可知,拱顶存在空洞时,拱顶处的弯矩方向发生反转,表现为拱顶外侧受拉,其余典型部位弯矩变化较小。当拱腰存在空洞时,弯矩最大值出现在空洞部位,表现为外侧受拉破坏。

(a)完好衬砌
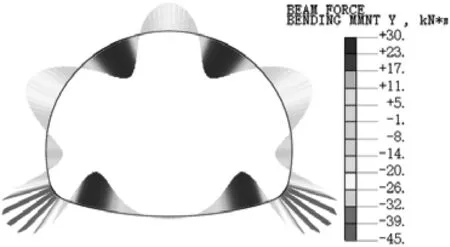
(b)拱顶空洞
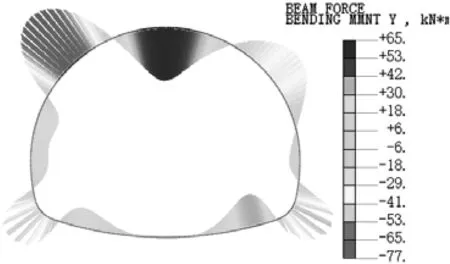
(c)左侧拱腰空洞
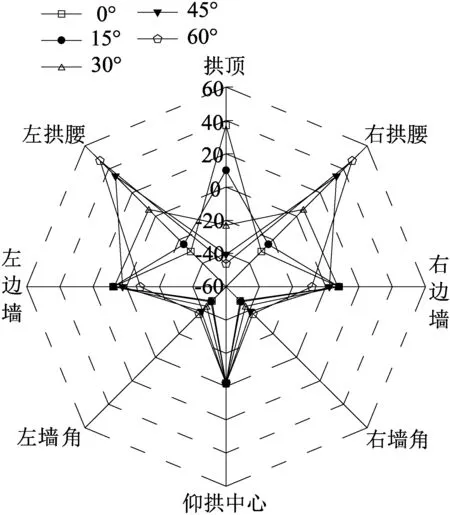
由图7可知,拱顶空洞时,随空洞范围的增大,弯矩图呈现“花瓣状”,具体表现为拱顶及临近部位弯矩方向发生反转,弯矩幅值先减小后增大。当拱顶空洞角度从0°增大到60°时,拱顶弯矩从37.14 kN·m变化到-45.79 kN·m,弯矩幅值增长了约23%。单侧拱腰出现空洞时,弯矩图表现为“羊角状”。随着拱腰空洞范围增大,拱腰及临近部位弯矩有增大趋势,而其他典型部位未见明显变化。当拱腰空洞角度从0°增至60°时,拱腰弯矩从-29.42 kN·m变化到-132 kN·m,弯矩幅值增大了3.49倍,拱顶及边墙部位弯矩则分别增大了55.49 kN·m和51.25 kN·m。总体而言,空洞存在的部位,其弯矩分布形态发生改变,且随着空洞范围的增大,衬砌受力条件恶化。
2.3 安全性分析
为反应衬砌安全性,计算衬砌各部位安全系数,将其最小值定义为衬砌最小安全系数。衬砌拱顶、单侧拱腰背后存在空洞时,采用三次多项式对不同空洞范围下的衬砌最小安全系数进行拟合,拟合相关系数(R2)分别为0.88和0.99,拟合度较好,结果如图8所示。图中采用线圈和箭头指出最小安全系数所属部位。
(a)拱顶空洞
(b)左侧拱腰空洞
由图8可知,拱顶存在空洞时,随着拱顶空洞范围增大,衬砌最小安全系数出现部位由墙角转至拱顶,最小安全系数随空洞范围增大整体呈下降趋势。当拱顶空洞范围在30°以内时,结构最小安全系数出现在墙脚,空洞范围增至45°及以上时,衬砌最小安全系数则出现在拱顶部位。拱顶空洞60°时,衬砌最小安全系数仅为无空洞时的65%。当单侧拱腰存在空洞时,衬砌的最小安全系数均出现在空洞处,拱腰空洞范围由0°增加至60°,衬砌的最小安全系数减小了80%。
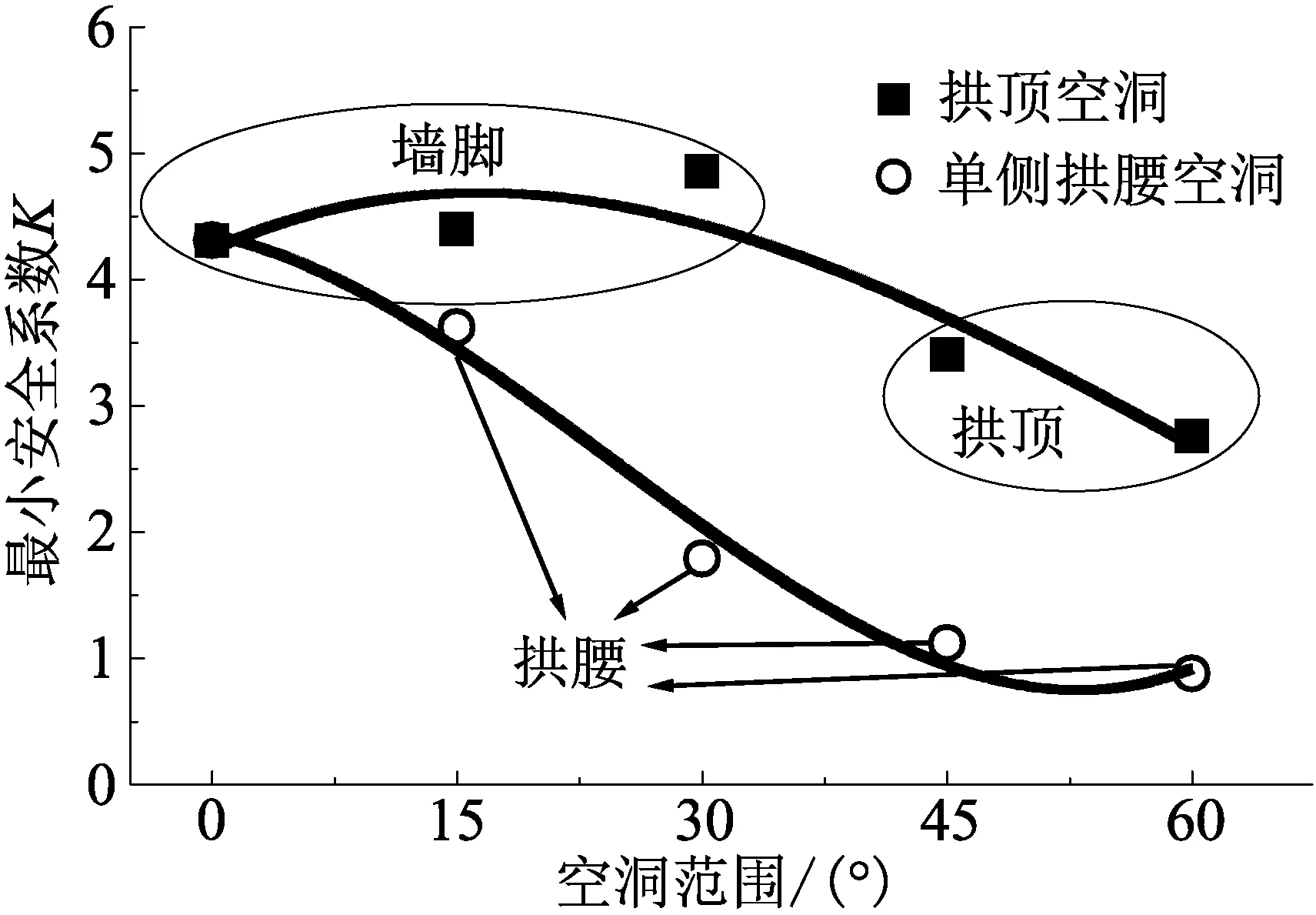
图8 最小安全系数变化曲线
相同空洞范围下,相较于拱顶空洞,单侧拱腰洞时,衬砌的最小安全系数更低。在空洞范围均达到60°时,单侧拱腰空洞的最小安全系数仅为拱顶空洞的31%。
3 结论
本文以存在空洞缺陷的衬砌为研究对象,建立了考虑空洞影响的围岩荷载-结构修正计算模型,通过算列研究了拱顶空洞、单侧拱腰空洞对衬砌内力和最小安全系数的影响,得出了如下主要结论:
(1)背后存在空洞时,衬砌受力条件恶化,空洞引起衬砌内力重分布,空洞处衬砌弯矩分布形态改变,且弯矩幅值呈增大趋势。
(2)拱顶或单侧拱腰存在空洞时,随着空洞范围增加,衬砌最小安全系数降低。
(3)相同空洞范围下,相较于拱顶空洞,拱腰空洞的安全系数更低。

