锻造过程中大截面塑料模具钢中空洞缺陷的闭合行为

吴柏良 陈 旋钟雨轩冯思远黎军顽吴晓春

(1.上海大学材料科学与工程学院，上海 200444； 2.省部共建高品质特殊钢冶金与制备国家重点实验室，上海 200444)

目前，许多发达国家的塑料模具钢需求量已经占据模具用钢的首位[1]。大截面塑料模具钢在凝固过程中空洞缺陷不可避免，因此需要热锻等大变形工艺使得空洞缺陷闭合，进而保证模具钢在服役期间的性能[2]。研究人员主要通过预制空洞的物理模拟和数值模拟，以及采用基于细观结构的代表体积元法研究锻造过程中空洞缺陷的闭合行为。尽管预制空洞的物理模拟能够比较直观地反映材料内部空洞缺陷的真实变形，但其可操作性差，同时预制空洞缺陷存在局限性，难以对不同锻造工艺、不同状态的空洞缺陷进行全面分析[3]。预制空洞的数值模拟过分简化研究模型，不能准确表征空洞缺陷的演变规律，提出的空洞闭合判据不够准确。例如，张建林[4]模拟了不同尺寸的空洞缺陷在拔长过程中的演变规律，结果表明：在空洞初始半径为5 mm的范围内，尺寸对空洞闭合的影响很小，并认为空洞形状为球形，而且粗略地假定空洞的初始半径范围，缺乏必要的空洞缺陷定量表征，因此难以揭示空洞的真实演变规律；Hideki等[5]通过预制贯穿钢锭的圆柱形空洞模拟得到了空洞缺陷的闭合判据，但由于过度简化研究模型，因而提出的空洞闭合判据不够准确。空洞尺寸与钢锭尺寸相差极大，空洞在锻造过程中的演变是一个多尺度问题，需在不同尺度上分别研究钢锭的锻造过程和空洞的闭合行为。代表体积元(RVE，representative volume element)是联系宏观和微观尺度的桥梁，能够准确反映空洞在锻造过程中的闭合行为[6]。例如，Saby等[7]借助RVE研究了力学参数对空洞闭合的影响，发现应变速率对空洞的闭合几乎没有影响，而应力三轴度对空洞的闭合影响极大；Lu和Chan[8]利用三维X射线CT和RVE方法定量预测了生物相容合金温锻过程中的损伤，并对不同应变水平下RVE中的损伤分布进行了可视化识别；Zhang等[9]借助RVE对大型铸锭热锻过程中空洞闭合的细观动力学进行了定量研究，建立了大钢锭锻造过程中的空洞闭合判定准则。然而，以往的研究主要关注RVE中单个空洞的闭合行为[7,9- 11]，忽略了锻造过程中空洞之间的交互作用。

鉴于以上研究现状，本文基于宏- 微观尺度模拟研究了大截面塑料模具钢锻造过程中内部空洞缺陷的闭合行为。一方面，采用宏观尺度有限元法模拟大截面塑料模具钢的锻造过程，根据模块的应变/应力演变结果选定空洞所在区域；另一方面，采用微观尺度RVE模型模拟锻造模块内空洞的闭合行为，包括单个空洞的闭合行为和空洞之间的交互作用。

1 大截面塑料模具钢中空洞缺陷的表征

试验材料为新型贝氏体预硬型塑料模具钢SDP1，试验钢经EAF冶炼、LF精炼、VD脱气及真空浇注冶炼而成，其化学成分(质量分数)为0.30%C、0.20%Si、2.20%Mn、1.40%Cr、0.28%Mo、0.008%N、0.003%S和0.015%P。采用光学显微镜和扫描电镜对钢锭内空洞进行定量统计表征。钢锭内空洞主要集中在帽口端和中心处。由于在钢锭中心取样困难，截取钢锭冒口端同一深度下尺寸φ15 mm×20 mm的试样，磨抛后根据GB/T 226—2015对试样进行冷酸腐蚀低倍检验。空洞缺陷的形貌如图1所示，主要为椭球形,随机分布。对扫描电镜摄制的60张金相照片中420个有效空洞进行统计分析，得到空洞的平均尺寸为50 μm，平均横纵比为1.4，该表征结果可为后续的RVE重构提供基础参数和依据。

2 大截面塑料模具钢锻造过程中空洞缺陷闭合行为的数值模拟

如图2(a)所示，采用有限元法模拟宏观尺度的锻造过程，分析锻造过程中大截面模块的应力/应变演变，根据应力/应变结果选取模块中具有代表性的点作为空洞缺陷所在区域，追踪所选点在锻造过程中的应力结果作为微观RVE锻造模拟的加载边界条件。在宏观锻造模拟中，大截面SDP1塑料模具钢模块尺寸为φ1 000 mm×2 200 mm，模块高度从2 200 mm锻压至950 mm，即压下率为56.8%。SDP1塑料模具钢的本构方程取自文献[12]。为了节约计算资源和时间， 对锻造模型作1/4简化。宏观锻造模拟还需作以下假设：上锻砧沿负z向以10 mm/s的速度下压，下锻砧保持不动；模块始锻温度为1 150 ℃，锻砧初始温度为200 ℃，环境温度为20 ℃；模块与锻砧之间的摩擦类型为剪切摩擦，摩擦因数为0.3，换热系数为11 000 W/(m2·K)[13]。

图1 大截面塑料模具钢内的空洞缺陷Fig.1 Void defects in the large- section plastic mold steel

如图2(b)所示，采用RVE方法从微观尺度研究锻造过程中空洞缺陷的闭合行为。根据空洞缺陷的定量表征结果实现RVE的重构。首先在RVE中设置单个空洞缺陷研究其在锻造过程中的闭合行为，然后设置水平排布和竖直排布的两个空洞缺陷研究它们之间的交互作用，最后研究复杂空间排布的空洞缺陷的交互作用。椭球型空洞缺陷的坐标轴尺寸分别为50、50和70 μm。为满足RVE均质化要求，RVE尺寸与单个空洞缺陷的尺寸比例为10∶1[14]。采用四面体单元划分网格，并将空洞缺陷附近的网格细分。RVE可视为宏观锻造模块中的一个点，追踪该点在锻造过程中的应力结果作为本文RVE的加载条件，并结合RVE的周期性几何边界条件(PBC，periodic boundary conditions)实现锻造过程的微观尺度RVE建模。

图2 大截面塑料模具钢锻造过程中空洞缺陷闭合行为的宏- 微观数值模型Fig.2 Macro- micro numerical model of the void defects closure in the large- section plastic mold steel during forging

3 结果与分析

3.1 大截面塑料模具钢锻造过程的应力/应变演变

图3为大截面SDP1钢模块在锻造过程中的等效应变和等效应力演变过程。由图3(a)可知，在低压下率下模块的应变极低，随着压下率的增大，应变逐渐增大，模块心部应变最大，最大值可达0.9，而其他区域的应变仅约为0.5。如图3(b)所示，随着压下率的增加，模块内应力超过15 MPa的区域逐渐向外扩大。模块按变形量大小依次可分为中心区的大变形区、环绕中心区的小变形区和锻砧接触面附近的难变形区。如图3(b)所示，分别在这3个变形区选取一点作为空洞缺陷所在局部区域，其中P1点位于大变形区，P2点位于小变形区，P3点位于难变形区。由于上锻砧的下压速度为10 mm/s，因此模块高度从2 200 mm锻压至950 mm共需锻造125 s。图4为锻造125 s过程中P1～P3点的三向应力演变情况，可见3点应力状态均不断变化。分别将这3点的三向应力作为RVE加载条件，模拟得到微观尺度下模块不同变形区中空洞缺陷的闭合行为。

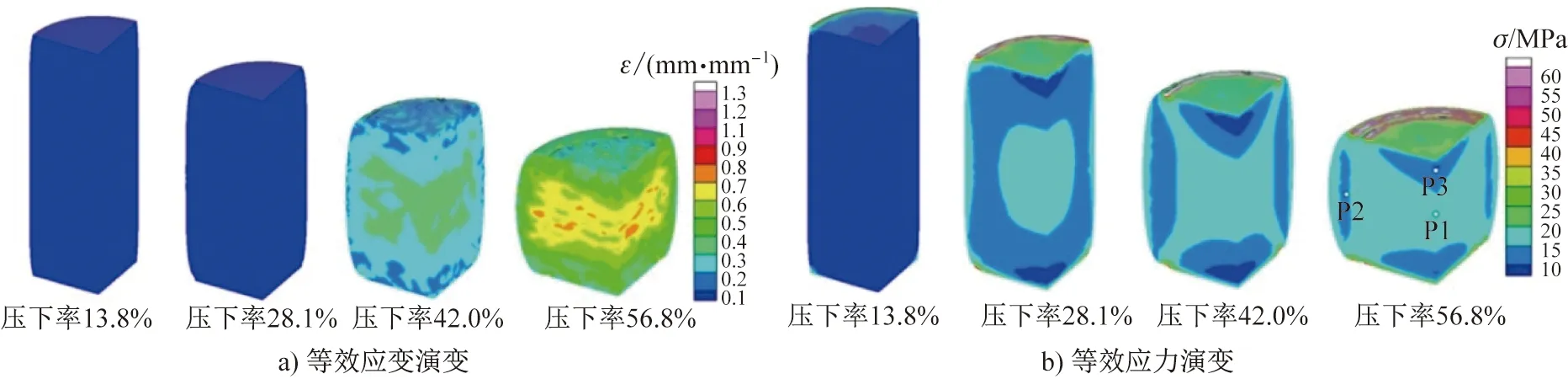
图3 大截面塑料模具钢锻造过程的等效应变/应力演变Fig.3 Effective strain/stress evolution of the large- section plastic mold steel during forging

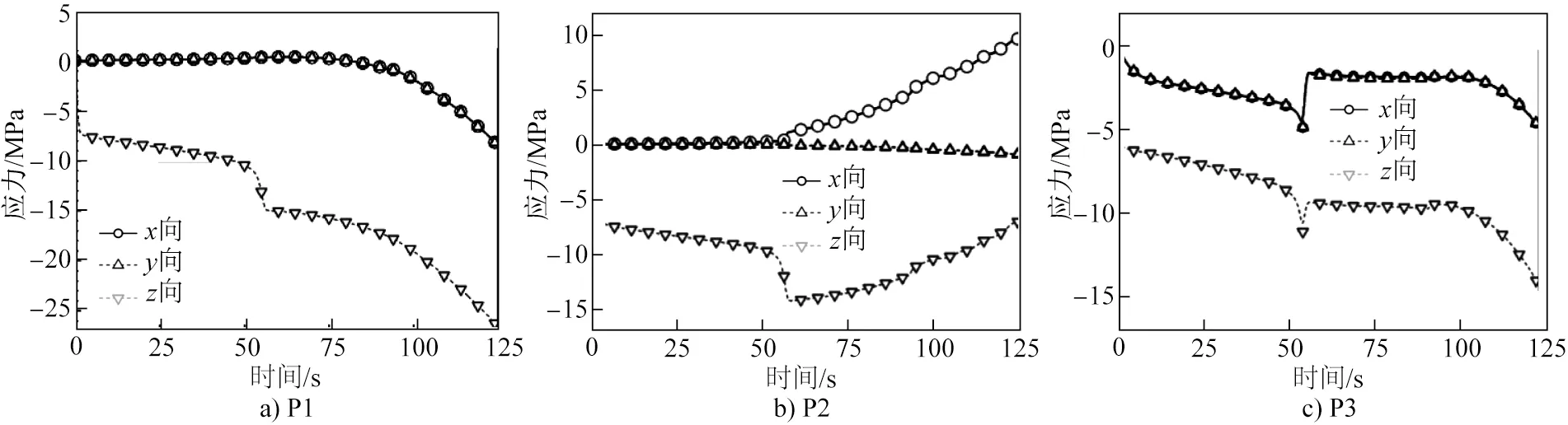
图4 P1～P3点在锻造过程中的三向应力演变Fig.4 Three- directional stress evolution at the points P1 to P3 during forging

3.2 单个空洞的闭合行为

P1点的单个空洞缺陷在锻造过程中的闭合行为如图5所示。可以发现，由于z向压应力较大(见图4(a))，P1点空洞的z向尺寸不断减小，而其余两个方向的尺寸不断增大，且z向尺寸的减小速率远大于其余两个方向的增速率。因此，随着压下率的增大，空洞逐渐由尖椭球形演变为球形、扁球形、裂纹，直至闭合[15]。如图6所示，模块中心P1点空洞在锻造过程中闭合。其余两点空洞的相对体积在锻造过程中也不断减小，但减小幅度远小于P1点空洞。P2和P3点空洞的相对体积最终约0.62和0.65，体积减小率仅为P1点空洞的38%和35%，因此空洞缺陷所在局部区域的变形量是其能否闭合的关键。

图5 P1点的单个空洞缺陷在锻造过程中的闭合行为Fig.5 Closure behavior of the single void defect at point P1 during forging

分析单个空洞缺陷在锻造过程中的等效应力场发现，根据等效应力大小RVE可分为3部分：第1部分为远离空洞且不受其影响的区域，其比例最大，定义为非空洞缺陷影响区；第2部分的等效应力大于非空洞缺陷影响区，位于空洞的周边呈纺锤状，定义为空洞缺陷的正影响区；第3部分的等效应力小于非空洞缺陷影响区，位于空洞的顶部和底部，即空洞缺陷变形最明显的区域，定义为空洞缺陷的负影响区。空洞缺陷的正负两个影响区范围在锻造过程中不断变化，压下率为22.7%时，空洞缺陷的正影响区范围约为空洞尺寸的4倍，负影响区范围约为空洞尺寸的2倍；而在压下率为45.5%时，正影响区几乎不存在，负影响区范围为空洞尺寸的10倍以上。

图6 P1～P3点的单个空洞缺陷在锻造过程中的闭合效率Fig.6 Closure efficiency of the single void defect at points P1 to P3 during forging

3.3 空洞缺陷的交互作用

空洞缺陷的负影响区可能对空洞闭合有重要影响。为了验证这一设想，分别在空洞缺陷的正负影响区设置另一个空洞(为确保产生交互作用，空洞之间的距离设置为0.01 mm)以探究空洞在锻造过程中的交互作用。水平排布表示在正影响区设置空洞，竖直排布表示在负影响区设置空洞。图7为P1点水平排布和竖直排布的两个空洞在锻造过程中的闭合行为。可以发现，位于同一个RVE中的两个空洞的闭合行为一致。这是因为RVE内两个空洞位置对称，应力状态也一致。水平排布空洞的闭合行为与单个空洞的闭合行为一致，因此每一锻造时刻空洞的相对体积与单个空洞的相对体积相等。两个空洞之间的正影响区虽然互相重叠，但与单个空洞的正影响区相比，其等效应力没有明显增大，而且两个空洞的负影响区仅在压下率为22.7%时有所接触，接触区域的等效应力十分接近非影响区， 因而对两个空洞的演变影响很小。因此，水平排布的两个空洞的闭合行为与单个空洞相近，几乎不存在交互作用。竖直排布空洞尽管体积在锻造过程中不断减小，但其减小速率远小于单个空洞，最终空洞没有闭合。两个空洞的外圆弧曲率在自身负影响区作用下越来越小， 这与单个空洞的外圆弧曲率演变规律一致。然而两个空洞之间的内圆弧曲率减小速率远小于其外圆弧曲率的减小速率，因此空洞内外两侧的变形不均匀，最终两个空洞变形至沙漏状。空洞之间的负影响区同时作用于上下两个空洞，但其应力水平与单个空洞的一致，因此在作用范围增加、应力大小一致的情况下，内曲率减小的趋势变缓，从而减缓了体积减小的趋势。因此，竖直排布的两个空洞在锻造过程中存在比较明显的交互作用，其闭合效率降低。图8为P1～P3点水平排布和竖直排布的两个空洞在锻造过程中的闭合效率。水平排布空洞的闭合效率与单个空洞的一致，而竖直排布空洞的闭合效率远低于单个空洞的闭合效率，其中P1、P2和P3点空洞仍保留了0.48、0.83和0.76的相对体积，体积减小率分别缩小了52%、20%和10%。

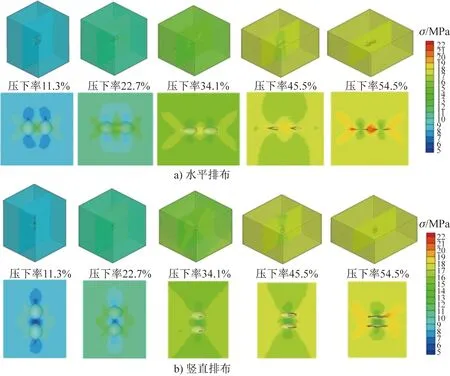
图7 P1点水平排布和竖直排布的两个空洞缺陷在锻造过程中的闭合行为Fig.7 Closure behavior of the two void defects of horizontal and vertical arrangement at point P1 during forging

3.4 空洞间距对空洞闭合行为的影响

在RVE中分别设置初始间距为0.01～0.05 mm的两个空洞，研究空洞间距对其闭合的影响，如图9所示。空洞间距对水平排布空洞的闭合几乎没有影响，不同间距的空洞闭合行为一致，而且在每一锻造时刻，空洞相对体积相差不大，空洞缺陷的正影响区对周边空洞的闭合几乎没有影响。空洞间距对竖直排布空洞的闭合影响很大，空洞闭合效率随着空洞间距的增大而增大， 间距为0.01～0.05 mm的空洞的最终相对体积分别为0.48、0.35、0.30、0.24和0.22，其闭合行为随着空洞间距的增大而更接近单个空洞的闭合行为。因此，空洞缺陷的负影响区对其周边的单个空洞尺寸范围内的空洞闭合影响较大。空洞初始间距在锻造过程中的演变如图10所示。可以发现，水平排布的空洞间距在锻造过程中不断增大，而竖直排布的空洞间距不断减小，最终在锻造80 s左右时稳定。竖直排布空洞的闭合效率随着空洞初始间距的减小而减小， 因此随着空洞间距的不断减小，竖直排布空洞的闭合效率比单个空洞的闭合效率低。图11为5种空洞间距的水平排布和竖直排布空洞的最终状态。可见水平排布的空洞最终安全闭合；竖直排布两个空洞的内侧最终曲率随空洞初始间距的增大而不断接近外侧最终曲率，空洞形态也从沙漏状逐渐转变为平行裂纹状。

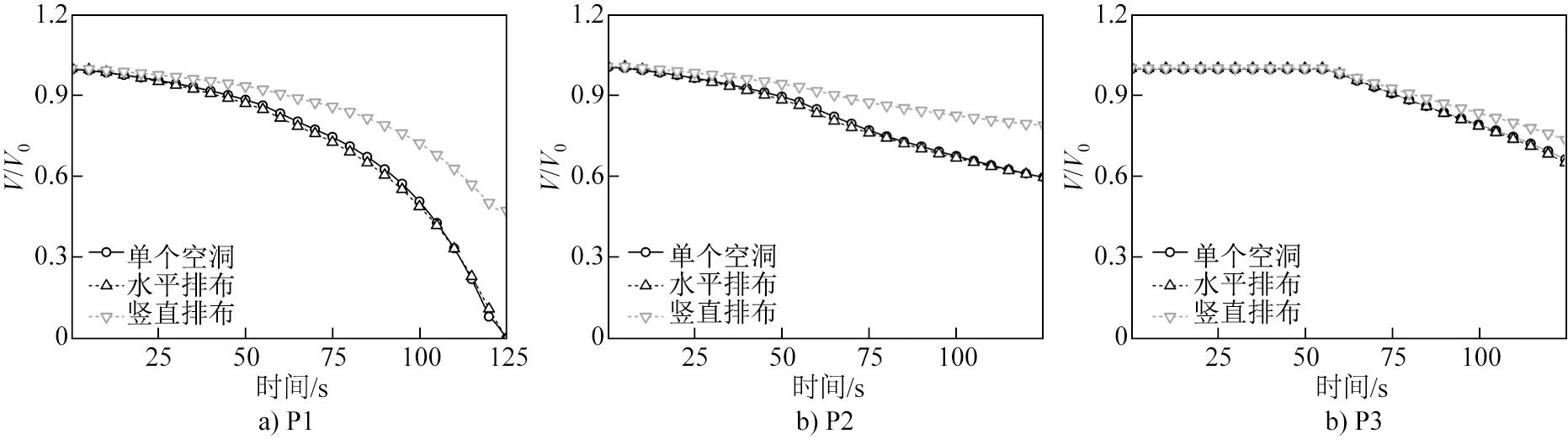
图8 P1～P3点水平排布和竖直排布的两个空洞缺陷在锻造过程中的闭合效率Fig.8 Closure efficiency the two void defects of horizontal and vertical arrangement at points P1 to P3 during forging

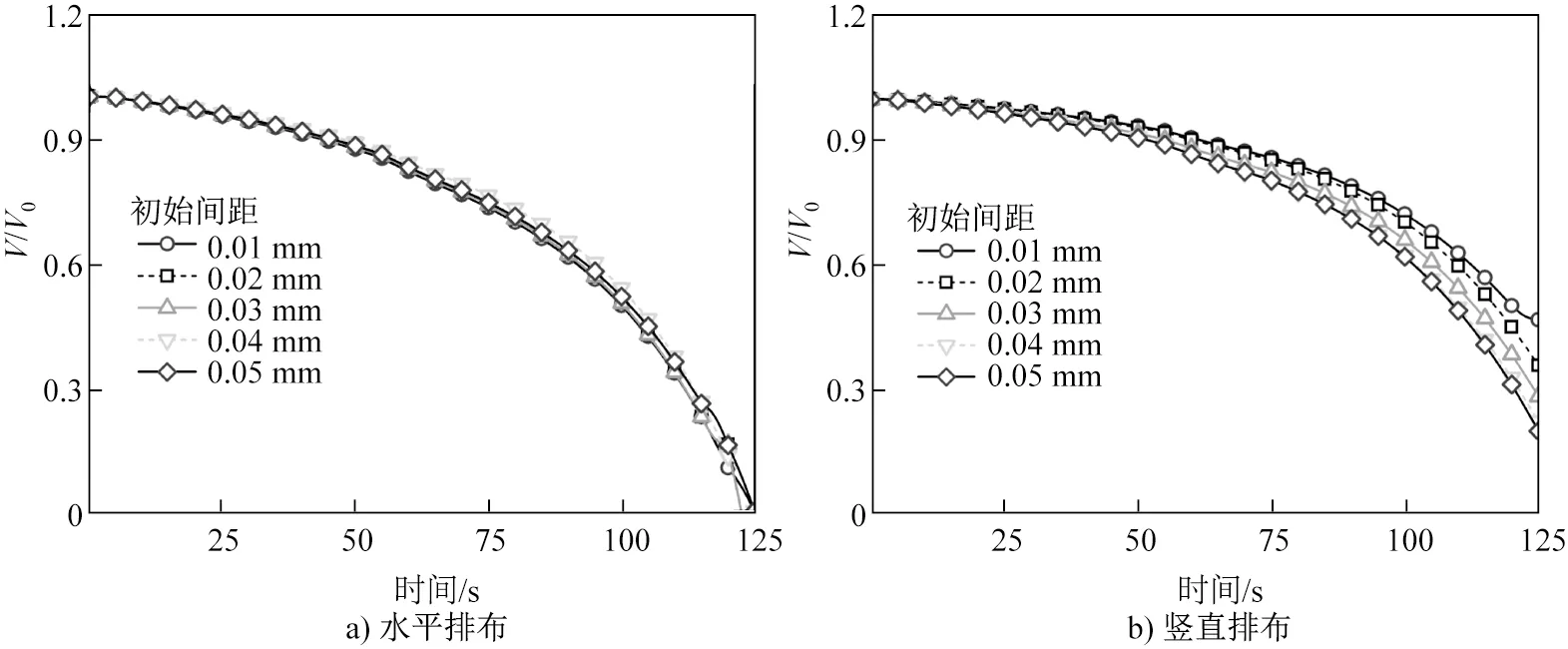
图9 水平排布和竖直排布的不同间距空洞的闭合效率Fig.9 Closure efficiency of the voids of horizontal and vertical arrangement with different spacings

图10 水平排布和竖直排布空洞的初始间距在锻造过程中的演变Fig.10 Evolution of initial spacing of the voids of horizontal and vertical arrangement during forging

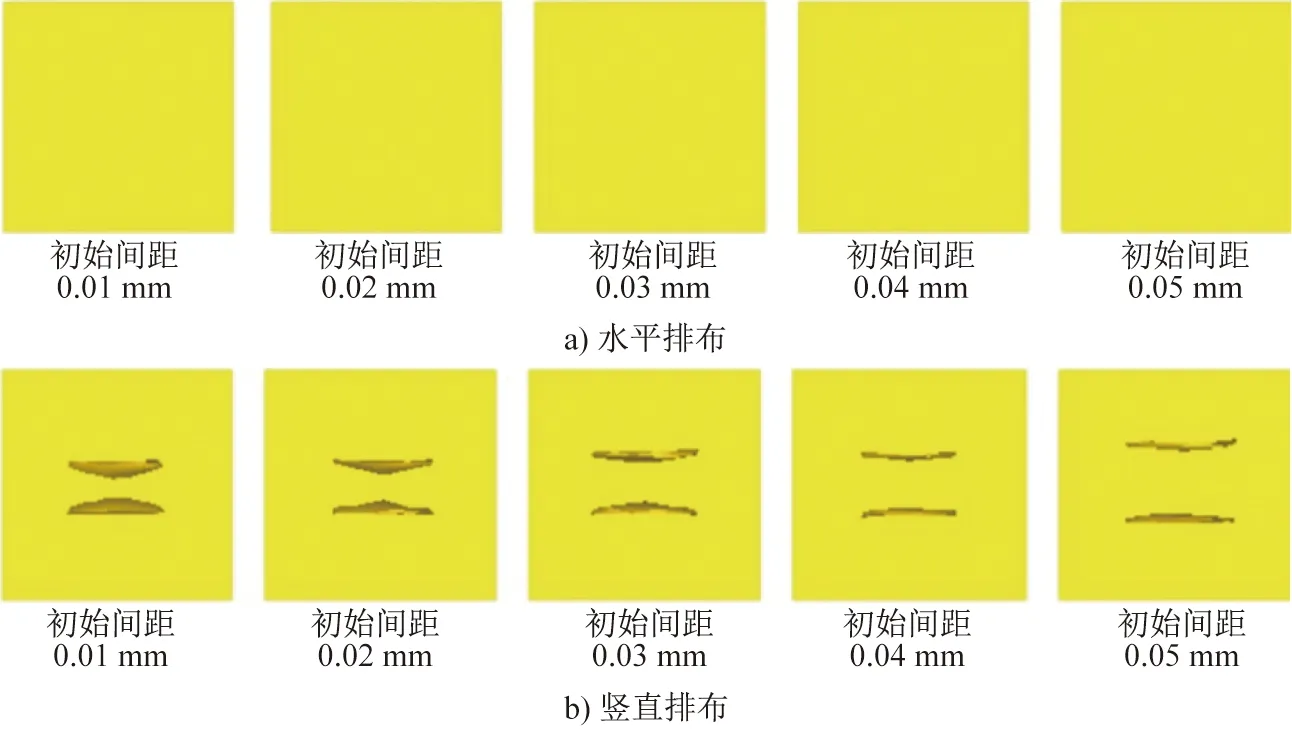
图11 水平排布和竖直排布的不同初始间距空洞的最终形态Fig.11 Final shape of voids of horizontal and vertical arrangement with different initial spacings

3.5 空洞的空间排布对其闭合行为的影响

在大多数情况下，钢锭中空洞的空间排布多样，其闭合行为比水平排布和竖直排布的交互作用更加复杂，因此需研究空洞的空间排布对其闭合行为的影响。如图12所示，首先定义空洞的取向，空洞的取向由θ和Φ这两个参数决定，θ为空洞的椭球长轴与坐标z轴的夹角，Φ为空洞长轴在xoy平面上的投影与x轴的夹角。模拟选取了3种空间排布(见图12)，第1种空间排布中两个空洞上下排布，上方空洞取向θ=0°，Φ=0°，下方空洞取向θ=45°，Φ=0°，表示为(θ=0°;θ=45°)；第2种空间排布的两个空洞的长轴共线，取向均为θ=45°，Φ=0°，表示为(θ=45°;θ=45°)；第3种空间排布的两个空洞为左右排布，左边空洞取向θ=45°，Φ=0°，右边空洞取向θ=-45°，Φ=0°，表示为(θ=45°;θ=-45°)。

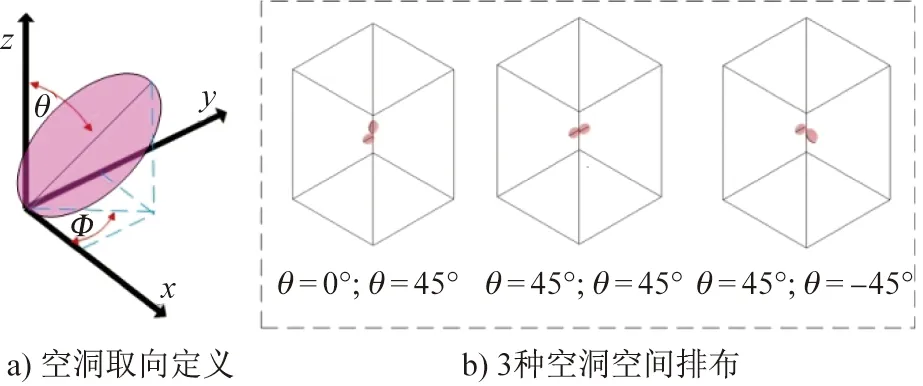
图12 空洞取向定义及3种空洞的空间排布Fig.12 Definition of void orientation and spatial arrangements of three types of void

如图13所示，这3种空间排布的空洞均未闭合，且空洞的剩余体积介于水平排布和竖直排布的之间，说明3种空间排布的空洞负影响区对闭合效率的减缓作用因排布关系而有所削弱。(θ=0°;θ=45°)空间排布时，尽管两个空洞的体积在锻造过程中不断减小，但两者的闭合行为不一致，上方空洞左侧的变形量远小于右侧，这主要与下方空洞负影响区的减缓作用有关，下方空洞按顺时针方向旋转，取向角θ不断增大至80°左右；(θ=45°;θ=45°)空间排布时，两个空洞的闭合行为比较一致，其长轴均按顺时针旋转，在每一锻造时刻，两长轴均为平行状态，最终取向角θ不断增大至85°左右，空洞剩余体积很小，且整体变形均匀，与单个空洞的闭合行为差别较小；(θ=45°;θ=-45°)空间排布时，左边空洞按顺时针旋转，右边空洞按逆时针旋转，最终二者几乎平齐，取向角θ增大至85°左右，空洞剩余体积很小。

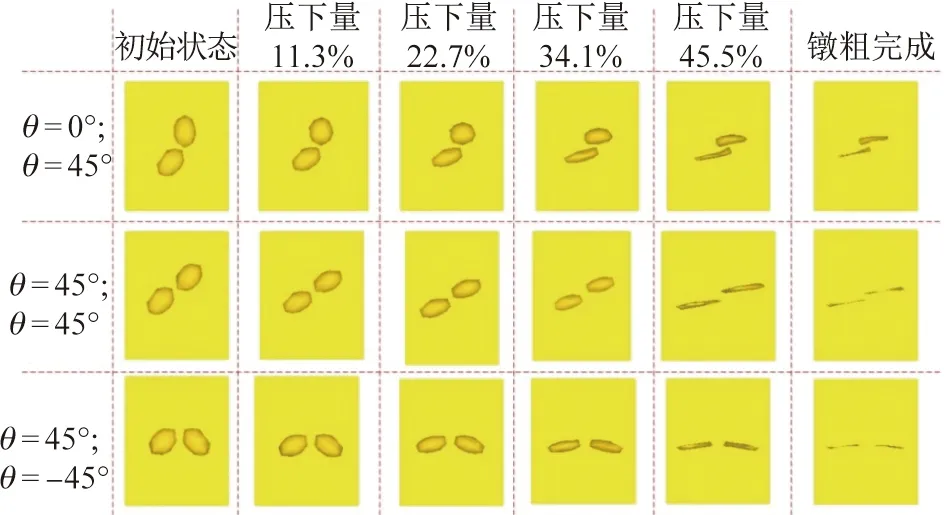
图13 空洞的空间排布对其闭合行为的影响Fig.13 Effect of the spatial arrangement of voids on their closing behavior

图14为不同空间排布的空洞的闭合效率。(θ=45°;θ=45°)空间排布和(θ=45°;θ=-45°)空间排布的空洞闭合效率较高，说明空洞的取向对其闭合影响很大。在该锻造过程中，载荷为负z向，因此空洞的取向角θ值越小，其自身闭合的可能性越小，所以(θ=0°;θ=45°)空间排布的上方空洞剩余体积最多。此外，在锻造过程中空洞的取向逐渐向载荷的垂直方向旋转，取向角θ值越大，空洞的闭合效率越大。除取向对闭合行为有影响外，空洞的位置排布也对闭合行为有很大影响。当空洞以平行于载荷方向排布时，闭合效率较低，因此竖直排布和空间排布(θ=0°;θ=45°)的空洞保留了较多的体积；当空洞以垂直于载荷方向排布时，闭合效率较高，因此水平排布的空洞闭合，(θ=45°;θ=-45°)空间排布的空洞剩余体积较少。因此，空洞交互作用是载荷方向、空洞取向和位置排布的综合结果。不同取向和位置排布的空洞的演化受载荷方向的影响，因此载荷方向是决定空洞交互作用的关键。在相同载荷方向，位置排布是通过改变负影响区位置而影响空洞交互作用的，空洞取向是通过改变空洞闭合距离而影响空洞交互作用的。尽管位置排布与取向对空洞交互作用的影响方式不同，但两者的影响程度相近，且均小于载荷方向的影响。

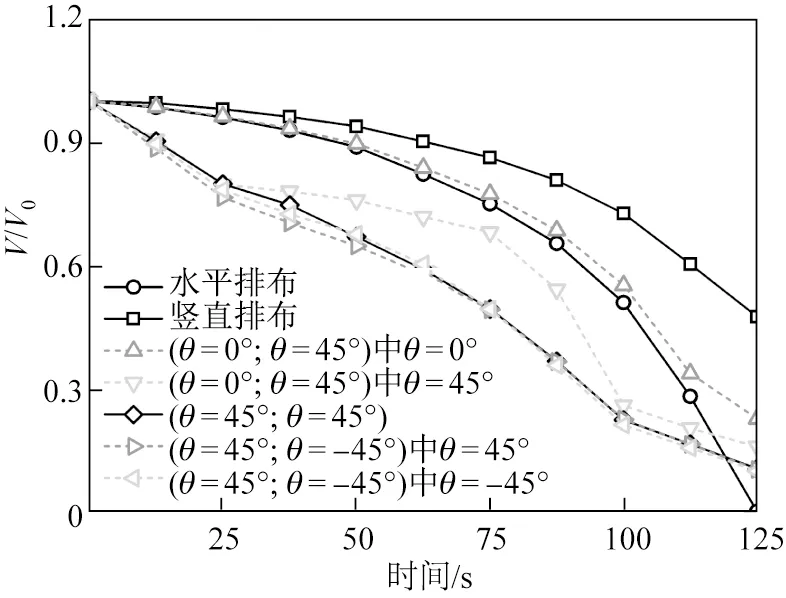
图14 不同空间排布的空洞的闭合效率Fig.14 Closure efficiency of voids of different spatial arrangements

4 结论

(1)单个空洞闭合行为表明：位于模块大变形区的P1点空洞在锻造过程中闭合，位于模块小变形区和难变形区的P2和P3点空洞仍保留了0.62和0.65的相对体积。

(2)空洞的交互作用表明：水平排布空洞的闭合行为与单个空洞的一致，而竖直排布空洞的闭合效率远低于单个空洞，P1、P2和P3点空洞仍保留了0.48、0.83和0.76的相对体积，体积减小率分别缩小了52%、20%和10%。

(3)随着空洞间距的增大，水平排布空洞的闭合行为保持一致，而竖直排布空洞的闭合效率与单个空洞的闭合效率趋于接近，间距为0.01～0.05 mm空洞的体积减小率分别为单个空洞的52%、65%、70%、76%和78%。

(4)载荷方向是决定空洞交互作用的关键，而空洞取向和位置排布对空洞交互作用的影响程度相近，且均小于载荷方向的影响。