香蕉串果夹持机构设计与试验

段洁利，易文峰，王红军，赵 镭，王 玉，杨 洲,2

(1华南农业大学工程学院，广东广州510642；2广东省山区特色农业资源保护与精准利用重点实验室，广东梅州514000)

近年来，随着我国农业劳动力的下降，收获高峰期找不到劳动力[1-3]，农业采摘机器人成为农业工程领域的研究热点[4-9]。夹持机构作为与农业生物对象直接接触的末端执行器是农业采摘机械装备的关键机构。目前国内外文献报道的夹持机构大多数针对体积较小、质量较轻的串形或单粒水果，如苹果、荔枝、葡萄和草莓等。尹建军等[10]设计的葡萄采摘机构中，用电机通过连杆机构驱动四指，从果实外包络抓取葡萄。苗玉彬等[11]设计的苹果夹持机构中，利用压力传感器测得所需要的夹持力，并将数值输给夹持末端，使得夹持力的数值比较精确。张凯良等[12]设计的草莓夹持器中，先利用摄像头定位，再通过2个光纤传感器探测机械爪中是否存在果柄，并进行切割，在切割的同时机械手对草莓进行夹持，一次性完成草莓的采摘。陈燕等[13]设计了具有4个自由度的结构，根据D-H坐标系建立了荔枝采摘机械手运动学模型并用于采摘荔枝。比利时的Baeten 等[14]研制出一种苹果采摘机器人，该机器人的手臂具有6个自由度，由液压升降装置驱动机械手臂作业。澳大利亚团队研制的香蕉采收机，以液压伸缩臂和切割机进行采收，节省了人力物力[15]。日本研制了一种由多自由度的机械手臂和视觉控制系统构建而成的葡萄采收器[16]。

中国是香蕉生产大国，与其他果蔬相比，香蕉属于串形水果，质量和体积大、果柄粗，难以用常规夹持机构夹持。人工采摘时，通常一人肩托着香蕉串、一人用刀砍断果柄[17]。本研究模拟人抱紧香蕉串的动作行为，设计了一种夹持蕉串果柄的末端执行机构，即内掌带钉抱掌夹持装置；通过搭建夹持试验平台，选择影响夹持效果的气缸压力、钉子数目以及钉子排列方式3个主要因素，采用单因素试验和响应曲面法进行了抱掌夹持力不同组合因素的效果测试，取得了较为理想的设计参数和试验数据，为夹持机构的进一步优化设计提供了理论和实践参考。

1 带钉抱掌夹持机构设计

模拟人工收获时手掌抱握对象的夹持方式[18]，本夹持机构设计圆弧形抱掌，通过抱掌内表面设置钉子增大抱掌与蕉柄间的附着力，设计的香蕉果柄夹持机构如图1a 所示。电机通过联轴器驱动丝杆转动，螺旋传动带动螺套往复运动，与螺套固连的抱掌在四杆机构驱动下实现张开与闭合。夹持机构推动抱掌闭合时，抱掌在抱紧蕉柄时的受力状态如图1c所示。

机构静力平衡关系如下：

式中，f1为钉子对蕉柄的挤压力，f2为连接杆对夹持杆的拉力，为连接杆和丝杆之间的夹角，为连接杆和夹持杆之间的夹角，f为夹持机构对蕉柄的挤压力。

由式(1)和式(2)可知，夹持机构对蕉柄的挤压力(f)是影响抱掌与蕉柄之间静摩擦力的主要因素，f是选择电机功率和螺旋机构设计的重要参数。为了轻量化夹持机构并获得可靠的夹持力，需要研究夹持因素对夹持力的影响规律，以获得优化的机构组合参数。

图1 夹持机构及受力图Fig.1 Clamping mechanism and force diagram

2 试验方法

2.1 夹持试验

2.1.1夹持力分析 夹持机构由螺旋机构和四杆机构组成。夹持过程中，抱掌通过螺旋机构带动四杆机构运动，获取作用在蕉柄上的压力，当蕉串从蕉柄上切割分离后，蕉串的质量(m)由抱掌与蕉柄之间产生的摩擦力( )承担(图1b)，抱掌夹持状态下与蕉柄截面受力示意图如图1d。由图1d 可知，夹持机构作用在抱掌上的挤压力(f1)、抱掌内表面钉子的排列方式和钉子数量是影响抱掌和蕉柄之间静摩擦力的主要因素，通过试验测试夹持各因素的影响规律及夹持效果，获取最佳组合参数。

2.1.2试验平台及试验材料 试验平台如图2a 所示，主要包括：万能试验机、抱掌、夹持元件、动力系统。抱掌由半圆形夹套和钉子(直径5 mm)构成，夹持元件由支撑平台、挡板和支柱组成，动力系统由空气压缩机、MGPM40-50Z气缸、手动换向阀、气源两联件和气管等组成。试验材料选用落梳后的果柄，切割成长度约为150 mm 的蕉柄段，方便放入抱掌中进行夹持试验。

图2 试验平台和原理图Fig.2 Schematic diagramsof experimental platform and principle

2.1.3试验过程 试验场景如图2b。测试过程中，由空气压缩机提供动力，经过气源两联件的减压阀调节输入气缸的气压大小，手动换向阀可调节气缸前进、后退和暂停3个档位。各元件安装好后，打开手动换向阀，抱掌在两侧气缸的推动下夹紧蕉柄，然后启动万能试验机。根据拉拔试验原理向上拉动蕉柄，模拟蕉柄切断后香蕉串的重力作用，测试抱掌对蕉柄的夹持效果，得出拉动过程中拉力和位移的数据信息，分析得到各因素对夹持效果的影响。

2.2 单因素试验

选取刚采收下来的香蕉果柄，裁截为便于夹持的蕉段，香蕉柄外形近似为圆柱形，蕉柄直径为60～70 mm，成熟度为7～8成熟。为获得气缸压强(即挤压力)、钉子数量和钉子排列方式对香蕉柄的夹持影响规律，分别对这3个因素进行单因素试验，每组试验分别进行3次拉拔试验，取平均值作为试验结果进行分析。试验取香蕉串质量30 kg 为载荷参照，安全系数取1.5，摩擦夹持情况下，夹持机构和蕉柄的最大静摩擦力为500 N 左右，可保持夹持机构能有效夹持蕉串。

单因素试验设计见表1。为测试气缸压强对夹持效果的影响规律，选取钉子的排列方式为X 型、钉子数量为10个、气缸直径为40 mm，拉拔速度5 mm/min。在气缸压强对夹持的影响研究中，确定了气缸压强至少0.40 MPa 可以稳定夹持，为此，控制钉子数量为10个、气缸压强0.40 MPa、拉拔速度5 mm/min；参考加工的方便性，分别选择钉子的排列方式为X 型、矩形和三角形，测试钉子的最优排列方式；选择气缸压强0.40 MPa 和矩形排列方式不变，钉子数量分别为4、6、8、10、12和14个，测试钉子数量的影响效果。

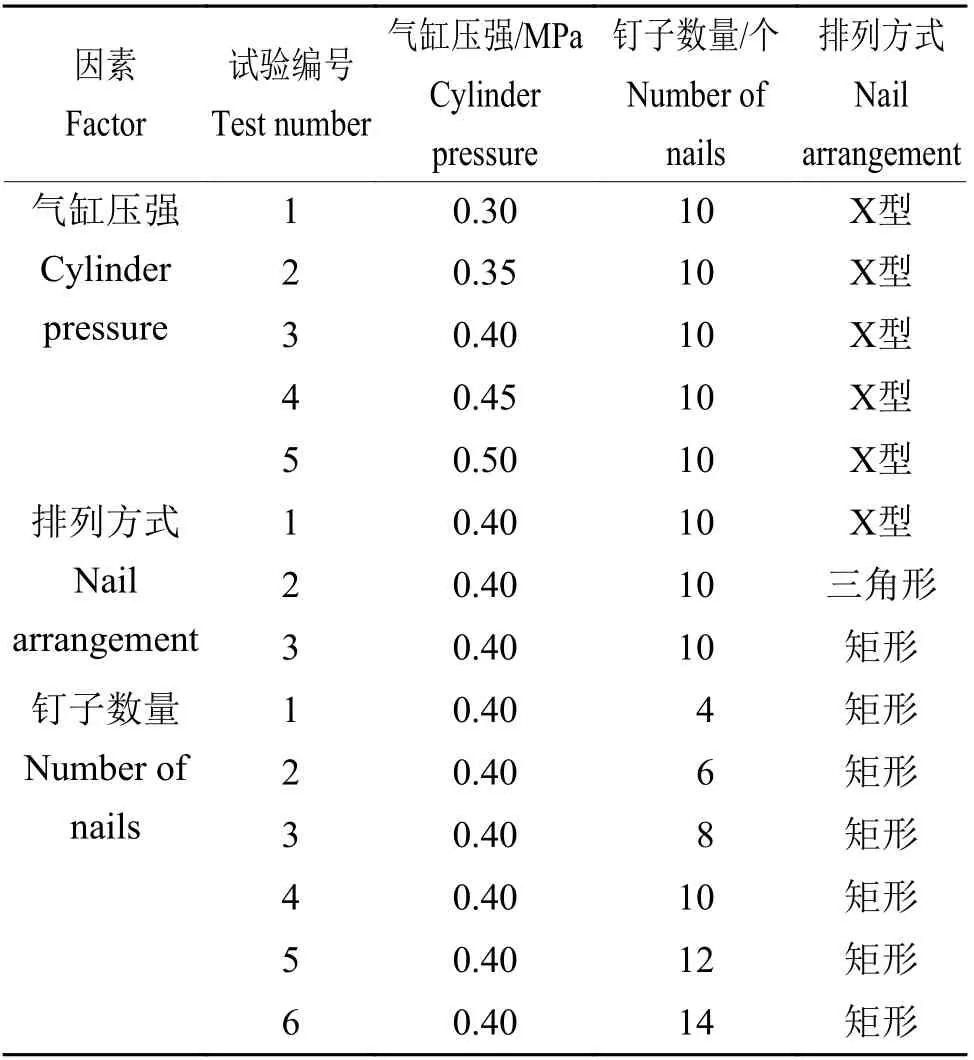
表1 气缸压强、钉子数量和排列方式单因素试验设计Table 1 Single factor test designs of cylinder pressure,number and arrangement of nails

2.3 响应曲面法试验

响应曲面法的设计模型主要是中心复合设计(Central composite design，CCD)[19-20]。为验证3个因素的组合夹持效果，本文采用CCD中的三因素三水平试验进行试验设计，测试气缸压强(x1)、钉子排列方式(x2)和钉子数量(x3)对夹持效果的影响，测试指标为拉力(即夹持机构承受的重力，y)，表2给出了因素编码及试验设计水平。利用Design-Expert 8.0.6软件对试验数据进行分析，采用线性和二次多项式拟合得出线性回归方程，确定最优的数学模型。

表2 因素编码及试验水平1)Table2 Factor coding and test level

3 结果与分析

3.1 单因素试验结果

3.1.1气缸压强对夹持的影响 拉拔过程中蕉柄的滑移受力曲线如图3a。由图3a 可以看出，拉力从零点至最高点的曲线段表示试验过程中蕉柄受力压缩阶段，此时拉力并未达到蕉柄和抱掌之间的最大静摩擦力；最高点为蕉柄和夹抱掌之间的最大静摩擦力点；最高点之后的曲线段表示蕉柄在拉力作用下平缓滑动，由于钉子的滑动使蕉柄表面破裂，蕉柄和抱掌之间的滑动摩擦力减小，蕉柄出现滑移，夹持失效。试验曲线表明，当气缸压强为0.35 MPa、拉力还未达到500 N 时，蕉柄在抱掌中产生滑移的现象，夹持失效；当气缸压强为0.40 MPa、拉力为500 N 左右时，最接近蕉柄和抱掌之间的最大静摩擦力，可以稳定夹持；当气缸压强为0.45或0.50 MPa、拉力达到600或800 N时，蕉柄在抱掌中出现滑移现象。

上述结果表明，气缸压强约为0.4 MPa 时，夹持状态最佳。查阅MGPM40−50气缸手册，气缸压强为0.4 MPa 时，气缸输出压力为500 N，即挤压力(f1)=500 N[21]。

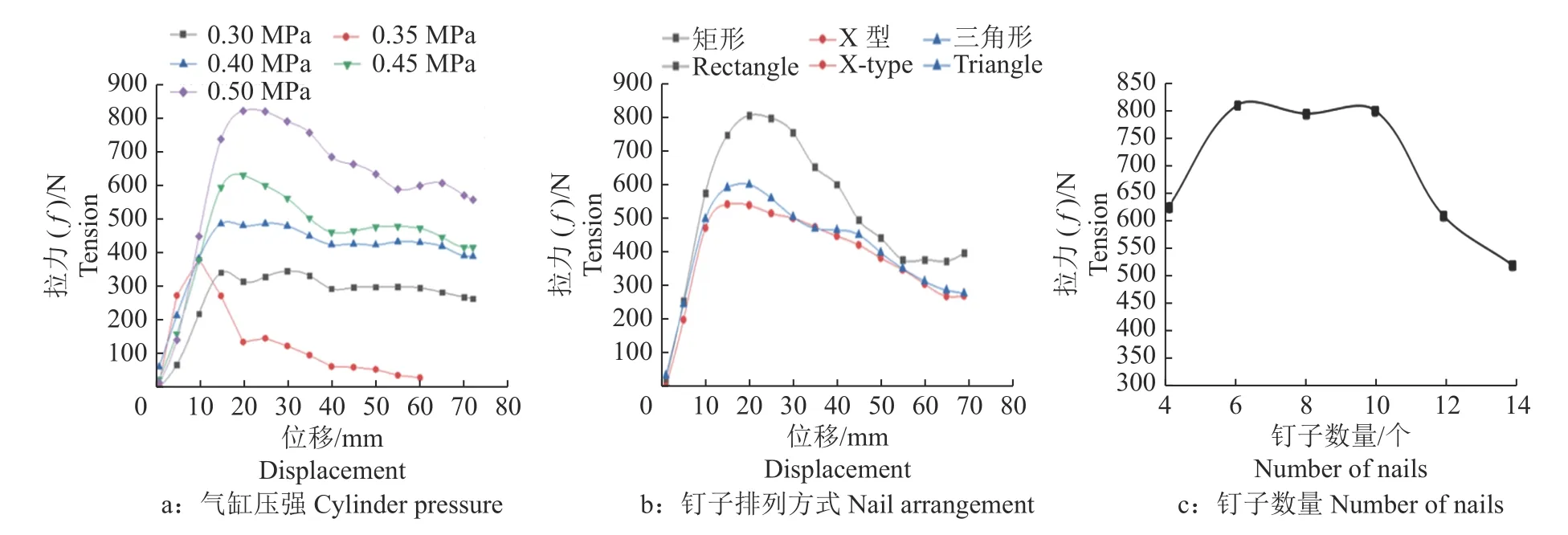
图3 气缸压强、钉子排列方式和钉子数量的拉拔试验结果Fig.3 Theresultsof drawing testsof cylinder pressure,nail arrangement and number of nails

3.1.2钉子排列方式对夹持的影响 图3b为不同钉子排列方式下，拉拔过程中香蕉柄的滑移受力曲线。从图3b可以看出，零点至最高点的曲线表示拉拔过程中蕉柄的受力压缩阶段，最高点之后是蕉柄在拉力作用下的滑动阶段。在气缸压强0.40 MPa、钉子数量为10个时，矩形排列方式拉力最大，最高点拉力为800 N，说明在滑动位移相同时，矩形可承受的摩擦力最大且最大值(fmax)为800 N，大于蕉柄和抱掌之间的fmax，因此，选择矩形的排列方式可以获得稳定的夹持效果。

3.1.3钉子数量对夹持的影响 图3c是蕉柄在不同钉子数量情况下可承受的最大拉力。由图3c可知，钉子数量分别为6、8和10个时，可承受的拉力均为800 N左右，大于蕉柄和抱掌之间的fmax，说明这3个水平均可获得稳定的夹持。钉子数量为8和10个时获得的拉力比较接近，并未因钉子数量增加而拉力增加，其原因可能是香蕉柄不是规则的圆柱形，导致圆形抱掌上的钉子并未全部扎进蕉柄内，钉子数量为8或10个时，只有6个钉子扎进蕉柄进行有效夹持。钉子数量超过10个后，拉力不升反降，出现该现象的原因可能是钉子越多，出现互相干扰的现象越严重，成为有效钉子的数量不升反降。试验结束后，观察蕉柄表面的滑痕，进一步印证了该结论。

3.2 响应曲面法的结果与方差分析

用Design-Expert8.0.6软件对试验因素进行分析，结果见表3。对表3中的数据进行回归拟合，保留显著性因素，对拉力进行二次回归方程方差分析，结果见表4。表4的结果表明，模型的P=0.000 2＜0.01，达极显著水平，拟合系数(R2)为0.9702；拉力失拟项的P=0.109 0＞0.05，不显著，这主要是因为蕉柄的表面不规则导致钉子有部分没有刺入，造成了试验误差。由于R2大于0.80，根据响应曲面法拟合系数的有效性参数原则，评价该系数有效，说明本试验采用的数学模型具有较好的拟合度。在设计的因素水平范围内，由各因素的F值大小得出各因素对拉力的影响，由表4可见，排列方式的二次项有较好的拟合度，各因素对拉力的影响大小依次为：排列方式的二次项效应(x22)＞气缸压强(x1)＞气缸压强与钉子数量的相互作用(x1x3)＞钉子排列方式(x2)＞钉子数量与排列方式的相互作用(x2x3)＞钉子数量(x3)＞气缸压强与排列方式的相互作用(x1x2)＞钉子数量的二次效应(x32)＞气缸压强的二次效应(x12)。

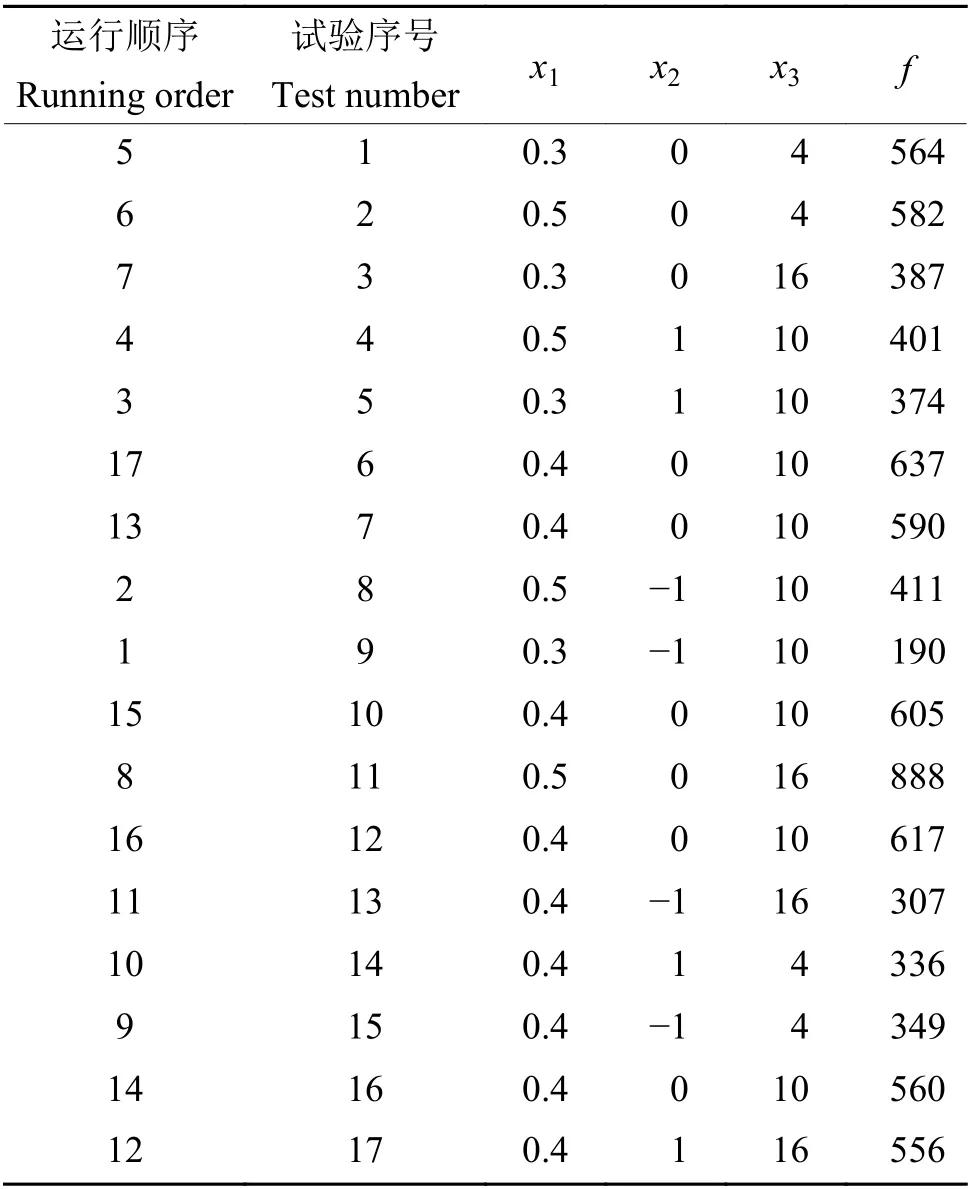
表3 响应曲面法的试验结果1)Table 3 Exper imental result by the r esponse sur face method

表4 拉力方差分析Table 4 Variance analysis of tension

3.3 两因素相互作用对拉力的影响

两因素相互作用对于拉力的影响和单因素的影响大致相同(图4)。钉子数量为10个时，气缸压强与钉子排列方式相互作用对拉力影响的3D响应曲面和等高线图见图4a1和4a2。由图4a 可以看出，气缸压强对拉力的影响更大，排列方式次之。在排列方式为矩形时，随着气缸压强的增大，拉力增大；在气缸压强一定时，排列方式对拉力的影响是先增大后减小。

气缸压强为0.4 MPa 时，钉子数量与排列方式相互作用对拉力影响的3D响应曲面和等高线图见图4b1和4b2。由图4b可以看出，钉子数量对拉力的影响更大，排列方式次之。在排列方式一定时，钉子数量增多，拉力增大；在钉子数量一定时，排列方式对拉力的影响是先增大后减小。

钉子排列方式为矩形时，气缸压强与钉子数量相互作用对拉力影响的3D响应曲面和等高线图见图4c1和4c2。由图4c可以看出，钉子数量和气缸压强对拉力影响均较大。在气缸压强一定时，随着钉子数量增多，拉力增大；在钉子数量一定时，随着气缸压强增大，压力增大。

图4 两因素相互作用对拉力的影响Fig.4 Effect of the interaction of two factorson tension

3.4 参数优化与验证结果

根据以上的分析，得到最优的参数组合，利用Design-Expert 软件的目标优化法，根据以下优化方程式：得出预测和实测的优化值，结果见表5。由表5可知，优化条件下的拉力预测值和实测值误差为4.6%，该误差在考虑范围内，即优化结果具有可参考性。拉力预测值和实测值的散点值差别如图5所示，预测拟合度高。表明气缸压强0.4 MPa、钉子数量10个、排列方式为矩形是抱掌夹持机构设计最佳组合。

表 5优化条件下预测和实测的优化值Table 5 Predicted and actual optimization valuesunder optimized conditions

图5 拉力预测值和实测值的散点分布Fig.5 Scatter distribution of predicted and actual tension values

4 结论

对于香蕉这类大质量串形水果的机械化采摘，可靠稳定的夹持方式是夹持机构设计的关键。本文通过搭建试验平台，进行夹持影响因素的单因素和正交试验测试，分析得如下结论：1)针对本次夹持装置中的研究对象，影响夹持效果的主次因素顺序为：气缸压强＞钉子排列方式＞钉子数量，最优组合为气缸压强0.4 MPa、钉子数量10个、钉子排列方式为矩形，此时，实测拉力524 N，大于最大静摩擦力，可以稳定夹持；2)在进行钉子数量的最优化试验过程中发现，当钉子数量超过一定数目时，实测拉力直线下降，甚至低于最大静摩擦力，原因是钉子数量过多，使蕉柄横截面破坏过大，蕉柄部分断裂；3)对于香蕉这种体积大的果蔬收获，传统摩擦式夹持机构难以保证稳定的夹持，为了保证香蕉从采摘到运输至指定地点的平稳，采用钉刺夹持方式具有可行性。