智能网联汽车路径跟踪控制器设计中模型预测的应用
德州职业技术学院 寇春欣
为了提高智能网联汽车在运动过程中的精确度,文章基于模型预测原理对智能网联汽车路径跟踪控制器进行了分析、设计和仿真,仿真结果表明,该控制器具有更好的灵活性,能够根据不同运行工况控制车辆,达到较高的跟踪精度和行驶稳定性,并为后续的研究提供重要的依据。
在国家大力发展先进制造业的背景下,智能网联汽车的研发设计成为汽车行业的重点研究方向。为了实现智能网联汽车的安全高效,对其路径跟踪控制器进行优化设计就成为了一项研究重点,通过该设备智能网联汽车就能够实现精准快速的主动转向行为,对解决各种路况下的车辆行进问题有着重要的作用。为此,仍需对这方面做进一步的研究。
1 车辆模型的构建
在本次路径跟踪控制器设计中,采用有着广泛应用的车辆二自由度单轨模型,且具有非线性轮胎力。在该单轨模型中,具有以下几点假设条件:(1)车辆始终在平整路面上行驶;(2)车辆的载荷转移和滑移情况不予考虑;(3)纵向驱动力的作用点为车辆的重心处。
为确保模型在满足实际要求的情况下计算精度尽可能高,设计人员通常会采用简化后的Pacejka轮胎模型,该模型的方程如式(1):

在该方程中,BR,CR,DR,BF,CF,DF的参数均通过实验确定,αF和αR则分别为前轮和后轮的侧偏角。
在基本模型构建完成后,为进一步提高精准度以获得高性能的控制器,还需要对轮廓误差进行分析计算。在这个环节中,首先要建立约束条件,约束条件主要包括控制量约束、增量约束、轮胎侧偏角约束和路面附着条件约束等车辆动力学相关内容。
一是对轮胎侧偏角进行约束,根据轮胎本身的性质,当轮胎侧偏角低于5°时,侧偏角和侧偏力之间存在线性关系,超过5°后则呈现非线性相关。根据小角度约束原理,前轮侧偏角的约束条件设定为[-2°,2°]。
二是对附着条件进行约束。路面的附着系数会在一定程度上影响汽车动力性能的发挥,特别是当路面附着条件恶劣时,车辆的动力性能会受到严重的限制;同时,如附着条件约束限定过小,还容易导致控制器的计算出现严重失真。为此,在本次研究中,设定路面附着系数为“软约束”,路面附着条件计算中存在一个松弛因子,路面附着条件约束则位于[ay,min-,ay,max+]之间。
在确定约束条件后,即可将车辆路径进行拟合,构建三阶样条多项式,通过求解该多项式即可得到参考路径上任一点的坐标。当然,这个坐标值和实际位置难免存在误差,该误差通过方程进行计算。
2 路径跟踪控制器的原理及组成
2.1 基本原理
在路径跟踪控制器工作时,其首先根据系统预测模型对一定时间段内的车辆运行状态进行控制,而后根据误差函数得到最优控制率。这一工作周期循环往复运行,以实现对智能网联汽车运行路径的持续优化。
2.2 控制器的组成
在本次设计中,采用MPC控制器作为路径跟踪控制器的主要模块,MPC控制器中集成了MPC算法,其包括预测模型、反馈校正、滚动优化这三个要素。由于其仅需计算标准的QP二次型即可解决系统输入限制,因此MPC控制器的应用也较为广泛。具体来看,其在运行过程中,首先会根据预测模型和当前的车辆运行状态,对预测周期内车辆运行的所有可能状态进行预测。在此基础上,该算法会生成包括预测误差在内的优化函数,最后在约束条件下对该优化函数进行求解,即可计算出最优控制输入,并以此来控制预测周期内的车辆运行路径。该运行呈现周期性的循环往复,如此即实现了“滚动优化”。
2.3 控制参数的选择
在模型预测控制器设计中,需要对采样时间、预测时域和控制时域进行设计。在不同的情况下,这三个要素可能会出现变化,特别是车速的变化对这三个要素的影响更为明显,因此本次研究中针对不同的运行速度,采用不同的控制时域和预测时域,并对采样时间进行相应修改。
为确保路径跟踪控制器在中低速和高速情况下均能起到预期效果,在本次研究中,分别考虑了这两种运行工况,对其参数进行了分别选择,如表1所示。

表1 控制器参数的选取
2.4 控制器的设计
控制器的设计主要通过MATLAB软件进行。在本次研究中,将St函数设置为车辆路径模型(亦可成为被控系统),该模型由四个微分方程组成,能够输出四个数据。该函数具有两方面的作用,一是接收控制器的输入,二是将控制器所需要的参数进行及时的反馈。控制器通过反馈即可得到当前时刻车辆运行轨迹的输出参数,再利用微分模型和欧拉法,对预测周期内的未来运行轨迹进行预判,得到未来最优控制量。对于其他的外界干扰因素,可用近似的模型加入到控制器所需要的预测模型当中;同时,为实现对转向机构的保护,还需要在控制器中加入转向角度的约束条件。
3 路径跟踪控制器虚拟仿真
为验证路径跟踪控制器的实际效果,在本次研究中采用车辆模型为控制对象。基于上文的研究结果,在Carsim平台和Matlab/Simulink平台,对其进行联合仿真。在仿真过程中,设计了直线路段、蛇形路段和双移线路段三种路段,分别模拟实际运行时的不同工况;同时,车辆初始位置在坐标系原点,路面附着系数设置为0.85。
通过一系列的仿真实验后发现,该控制器在车辆模型的中低速和高速工况下,其路径跟踪效果均较好,特别是在车辆以中等速度(50~60kph)运行时,其几乎不存在轨迹跟踪误差。当然,在高速运行工况下,该控制器仍然在直线路段和弯道交叉点附近存在微小的误差,局部误差超过0.6m。分析误差出现的原因,可能是由于该路段的过渡路程较短,且车速较高所致。
在车辆模型的运行过程中,车辆的前轮转角、纵向加速度、横摆角速度和质心侧偏角的相关数值也出现了细微的抖动,通过理论分析,推断是因纵向加速度过大,导致轮胎的侧偏特性处于非线性区。
在本次仿真实验测试中,测试结果如表2所示。
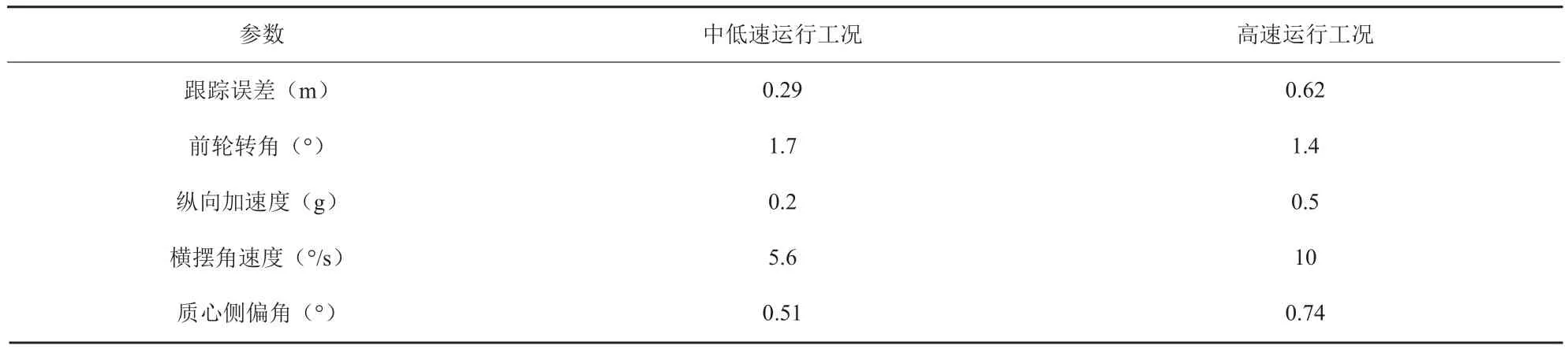
表2 不同工况下各状态量绝对值对比
根据表2中的数据可知,各状态量的绝对值大多数都处于合理范围内,仅在高速状态下的横摆角速度略为偏大,通过分析发现,横摆角速度偏大的情形主要出现在蛇行路段的顶点处,此处路径弯曲程度过大,且车速也过高,属于极特殊情况。整体来看,该控制器控制下的车辆模型能够在日常的各种工况下保持良好的运行状态,且控制器的跟踪精度也较好。
结束语:在本次研究中针对智能网联汽车的路径跟踪控制问题,提出了一种基于模型预测的智能网联汽车路径跟踪控制器的设计方法,在设计中综合考虑了汽车的不同运行工况,分别进行了针对性的设计,以确保其具备较高的跟踪精度。对设计结果进行仿真后表明,本次设计的路径跟踪控制器效果相对较好,对后续的研究实验具有一定的参考价值。当然,由于本次仅为仿真实验,与真实路况仍有一定的差距,因此在今后的研究中仍需对此进一步完善。

