地铁直线轨道钢轨波磨影响参数研究
王志强 雷震宇
1. 同济大学铁道与城市轨道交通研究院,上海,201804 2. 上海市轨道交通结构耐久与系统安全重点实验室,上海,201804
0 引言
钢轨波磨为轨道线路上显著的损伤问题,如何有效地抑制和消除波磨是铁路行业一百多年来研究的一大热点。钢轨波磨不仅影响轨道的动态响应[1-2],也会对车辆产生不利的振动影响[3-4],甚至会影响轮轨匹配关系[5]。轻度的钢轨波磨可以通过钢轨打磨去除[6],严重波磨的钢轨则只能通过更换新轨来维持行车舒适性和保障行车安全。但是无论哪种维护方式,都会大大增加铁路工务部门的维修工作量和维护费用。
为了降低和消除钢轨波磨带来的影响和危害,国内外学者综合采用现场测试、数值仿真和试验研究的方法对钢轨波磨产生和发展的影响因素展开分析,提出了许多控制和消除钢轨波磨的工程措施。MEEHAN及其团队[7-10]建立了磨耗型波磨的反馈模型,并利用该模型从车辆速度变化对波磨产生和发展的影响角度对钢轨波磨进行了全面的研究:通过建立速度概率模型,分析了不同速度分布下钢轨波磨的发展情况,结果发现非均匀速度分布模式相对于均匀速度分布模式可以更有效地控制钢轨波磨的发展,从而提出通过改变列车运行速度来减缓波磨发展的措施。SUN等[11]研究了车轮磨耗对钢轨波磨的影响,发现车轮磨耗后锥度变大,使得车轮更容易通过曲线轨道,从而使得轮轨间蠕滑率相应减小,降低了钢轨波磨的发生概率。EGANA等[12]通过添加摩擦调节剂来控制轮轨间的蠕滑力,以延迟和抑制钢轨波磨的产生,并且通过实验验证了该方法的适用性。DANIEL等[13]通过建立波磨时域和频域模型,分析了使用摩擦调节剂后钢轨波磨的发展情况,结果发现摩擦调节剂可以使轮轨间达到低蠕滑和低牵引的状况,使轮对的转弯状态改变,达到全滚动的状态,从而消除轮轨摩擦自激振动,避免钢轨波磨的产生。闫子权等[14]根据现场试验测试研究了动车轮对和拖车轮对的垂向振动和扭转振动对钢轨波磨的影响;尤其研究了动车轮对的电机位置对钢轨波磨的影响,发现电机处于轮对上的任意位置均会导致钢轨波磨的产生,说明电机位置对钢轨波磨的影响较小,并且得到引起波磨的不稳定振动频率处于285~300 Hz范围内[15]。YAN等[16]运用遗传算法对北京地铁梯形轨枕支撑轨道结构进行了数值分析,通过改变扣件参数分析高频振动特性,改变轮轨材料参数分析低频振动特性,并综合考虑各参数以控制轮轨共振发生,从而降低钢轨波磨发生的概率。基于非线性钢轨磨耗型波磨数值模型,JIN等[17-18]分析了直线和曲线轨道离散支撑对钢轨波磨的影响,结果发现离散的轨道支撑结构会导致不同波长钢轨波磨的产生。任彤等[19]通过锤击法对某地铁曲线线路的GJ-32扣件、先锋扣件与科隆蛋扣件进行了垂向、横向频响特性测试,并结合实测波磨数据对小半径曲线段钢轨短波波磨进行了研究,发现不同扣件结构形式下钢轨的垂向弯曲共振不是小半径曲线段钢轨出现波磨的主要原因。王洪刚等[20]从轮轨蠕滑力和磨耗功率的角度研究了小半径曲线钢轨波磨问题,并对车辆运营速度和线路曲线半径的选择提出了建议。
目前地铁线路中已有的波磨治理方法主要有钢轨打磨、钢轨表面涂润滑剂、调节轮轨摩擦因数以及提高钢轨材料硬度等。除上述方法外,大量学者也在从优化影响钢轨波磨的结构参数和运营参数等角度研究如何控制波磨的产生和发展。本文主要基于车辆-轨道耦合动力学模型和钢轨材料摩擦磨损计算模型,采用控制变量法分析不同轨道结构参数和车辆运营速度对直线轨道钢轨波磨发生和发展的影响,从而为抑制钢轨波磨产生和发展的参数优化提供参考。
1 车辆-轨道耦合模型
1.1 车辆模型
以地铁A型车为研究对象,车辆主要参数如表1所示[21]。采用多体动力学软件UM(universal mechanism)建立多刚体系统车辆模型,模型包括车体和2个转向架,每个转向架包括2个轮对,共计4个轮对。车体、转向架和轮对均视为刚体,具有质量和转动惯量,车轮踏面为LM磨耗型踏面。车体与转向架、转向架和轮对之间均通过弹簧阻尼单元连接,以模拟一系、二系弹簧,具有3个方向上的刚度和阻尼。
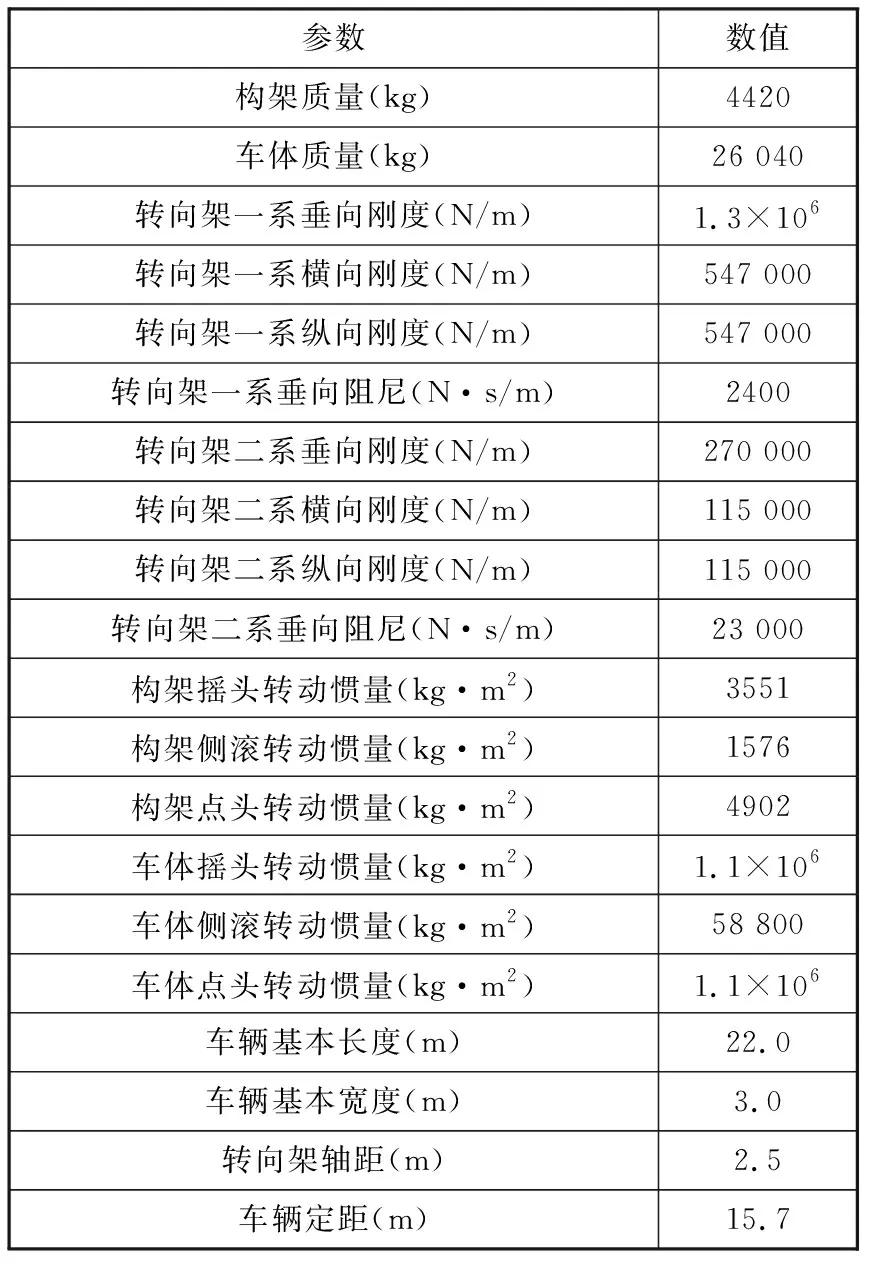
表1 车辆主要参数Tab.1 Main parameters of vehicle
1.2 轨道模型
轨道模型采用柔性轨道模型,钢轨模拟采用考虑剪切变形的Timoshenko梁,Timoshenko梁能较好地反映钢轨高频振动的影响,适合研究波磨问题;扣件部分模拟采用Bushing力元,它可以考虑3个方向上的刚度和阻尼[22-23];道床板部分通过有限元软件ABAQUS建立三维实体单元模型并将模型导入到UM前处理中,作为动力学模型的一个子系统,道床板断面尺寸为2700 mm×300 mm,长度为60 m。道床板与地基的连接以及道床板与钢轨的连接都是通过力元进行模拟的,连接部分各参数取值如表2所示[24]。
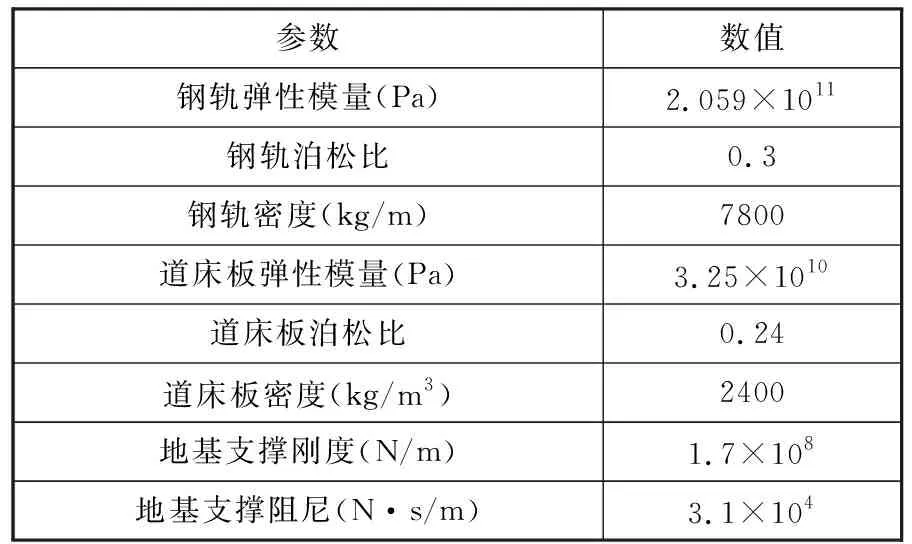
表2 轨道结构参数Tab.2 Parameters of track structure
1.3 轮轨接触模型
轮轨接触模型采用Kik-Piotrowski接触模型,其法向接触应力通过接触区域的几何点是否能够满足接触条件求得,切向接触应力通过改进的FASTSIM算法求解。该模型能够适应轮轨非赫兹接触的情况[25]。
1.3.1法向接触模型
根据轮轨表面之间的虚拟穿透量δ0和间隙f(y)确定虚拟穿透区域,轮轨接触时的渗透量g(y)可通过下式进行计算:
(1)
当轮轨接触渗透量大于0时,轮轨接触斑前端和后端边界的计算公式如下:
(2)
该值可用于确定轮轨接触区域。其中,xf(y)和xt(y)为轮轨接触斑的前后边界;R为刚性接触点位置处的车轮滚动圆半径。根据赫兹接触理论中法向接触应力的分布假设(沿车轮滚动方向的轮轨法向接触应力分布为半椭圆形),可得法向接触应力的表达式:
(3)
式中,p0为最大法向接触应力;x、y为轮轨接触斑内节点的坐标。
假设p0为已知,则轮轨法向力可通过接触区域内的法向接触应力积分得到:
(4)
式中,N为轮轨法向力;yl、yr分别为轮轨接触斑的左右边界。
为了确定轮轨法向接触应力的最大值,认为仅在轮轨刚性接触点位置处(x=0,y=0)满足接触条件的要求。使用Boussinesq函数计算轮轨刚性接触点位置处的法向位移h0:
(5)
式中,ν为泊松比;E为弹性模量。
轮轨法向刚体穿透量δ与刚性接触点位置处的法向位移h0之间的关系满足
δ=2h0
据此,联立式(4)和式(5)可得
(6)
根据式(6)即可解决法向接触问题,该方法可靠性高,计算速度快。
1.3.2切向接触模型
假设不考虑接触区域内的轮轨滑动,则切向接触应力的分布为
(7)
式中,νx、νy、φ分别为纵向、横向和自旋蠕滑率;L为接触面积弹性参数值。
通过对式(7)积分可得接触区域内切向力计算公式:
(8)
式中,Fx、Fy分别为纵向蠕滑力和横向蠕滑力。
基于车辆模型、轨道模型和轮轨接触模型构建车辆-轨道耦合动力学模型,如图1所示。
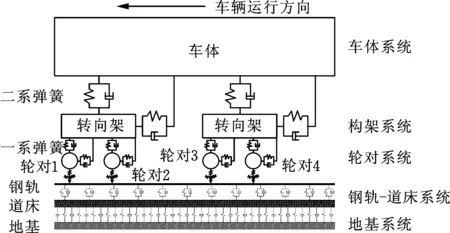
图1 车辆-轨道耦合模型示意图Fig.1 Schematic diagram of vehicle-track coupled model
1.4 模型验证
为保证后续计算的正确性和有效性,本节对上文所建立的车辆-轨道耦合动力学模型进行验证。由于轮轨的动力学特性与车辆-轨道耦合系统密切相关,具体的车辆-轨道耦合系统决定了相对应的轮轨动力学特性,而轮轨动力学特性可以相应地表征出车辆-轨道耦合系统的固有特性[26],因此,利用试验和仿真所得的钢轨或轮对的振动值作为系统模型的验证是可行的。本节采用的实测数据为地铁线路的钢轨垂向振动加速度级。测点断面布置2个传感器,分别位于钢轨轨底顶面两侧。数据采集使用INV3060S采集仪,数据采样频率为1024 Hz,速度工况为60 km/h,数据分析使用DASP-V10软件。测点布置及现场测试照片如图2所示。

图2 现场测试照片Fig.2 Field test picture
初始不平顺值采用实测线路钢轨表面不平顺值,轨道结构参数参照实际线路取值,基于车辆-轨道耦合动力学模型,对实测地铁线路进行仿真计算,提取测点断面钢轨垂向振动加速度数据,并与实测数据进行对比,结果如图3所示。分析可知,仿真结果与测试结果具有较好的一致性,误差最大不超过8 dB,表明仿真模型满足本文计算精度要求,从而验证了模型的有效性。

图3 仿真与实测结果对比Fig.3 Comparison of simulation and measurement results
2 轨道结构参数
由于目前地铁线路上不同区段的减振要求不同,故相应区段采取的轨道支撑结构也不同。根据扣件的减振性能,地铁轨道大致可以分为高弹性减振扣件轨道(Vanguard扣件、科隆蛋扣件等)、中等弹性减振扣件轨道(Lord扣件、GT型弹性扣件等)和一般弹性减振扣件轨道(DT型弹性扣件、WJ型弹性扣件等),且上述弹性扣件轨道的扣件垂向静刚度大约处于8×106~52×106N/m范围内[27]。
本文轨道结构参数主要选取扣件垂向刚度KRZ、垂向阻尼CRZ、横向刚度KRY、横向阻尼CRY、纵向刚度KRX、纵向阻尼CRX、扣件间距d以及轮轨摩擦因数μk这8个影响因素。参考文献[24,27-28]可得轨道结构参数的变化范围如表3所示。由于扣件的横向刚度和纵向刚度、扣件的横向阻尼和纵向阻尼通常是相等的,所以在分析过程中其变化范围和趋势保持一致[24,29]。

表3 轨道结构参数变化范围Tab.3 Variation ranges of track structure parameters
采用控制变量法分别对轨道结构这8个主要影响因素展开研究,分析其对钢轨波磨发生和发展的影响。首先,选取各个影响参数的中间值作为基准值,即KRX=KRY=KRZ=25 MN/m,CRX=CRY=CRZ=5000 N·s/m,d=0.7 m,μk=0.4。需要说明的是,之所以选取各参数的中间值作为基准值,是为了使各参数值具有上下浮动的区间并保持上下浮动区间的均匀性,从而更有利于研究各参数对钢轨波磨的影响程度及趋势。然后,在固定控制变量的前提下,通过改变单个影响因素,研究其对钢轨波磨发生发展的影响。其中,钢轨波磨发展的程度主要通过摩擦功率这一变量来衡量。仿真过程中,将实测波磨不平顺值作为钢轨表面不平顺值。现场实测波磨照片、不平顺值及1/3倍频程波长的不平顺等级见图4。图4c中显示钢轨波磨特征波长范围为80~200 mm。由于线路实际车速约为60 km/h,因此特定波长λ对应的通过频率f可根据公式f=v/λ得到,为83~208 Hz。本文中钢轨表面不平顺度采用轨道综合检测车进行测量,该设备取样步长为5 mm,系统分辨力为0.01 mm,系统精度为0.025 mm,检测速度为4 km/h。参照实际车速,仿真模型中的车速设为60 km/h。

(a) 现场实测波磨照片
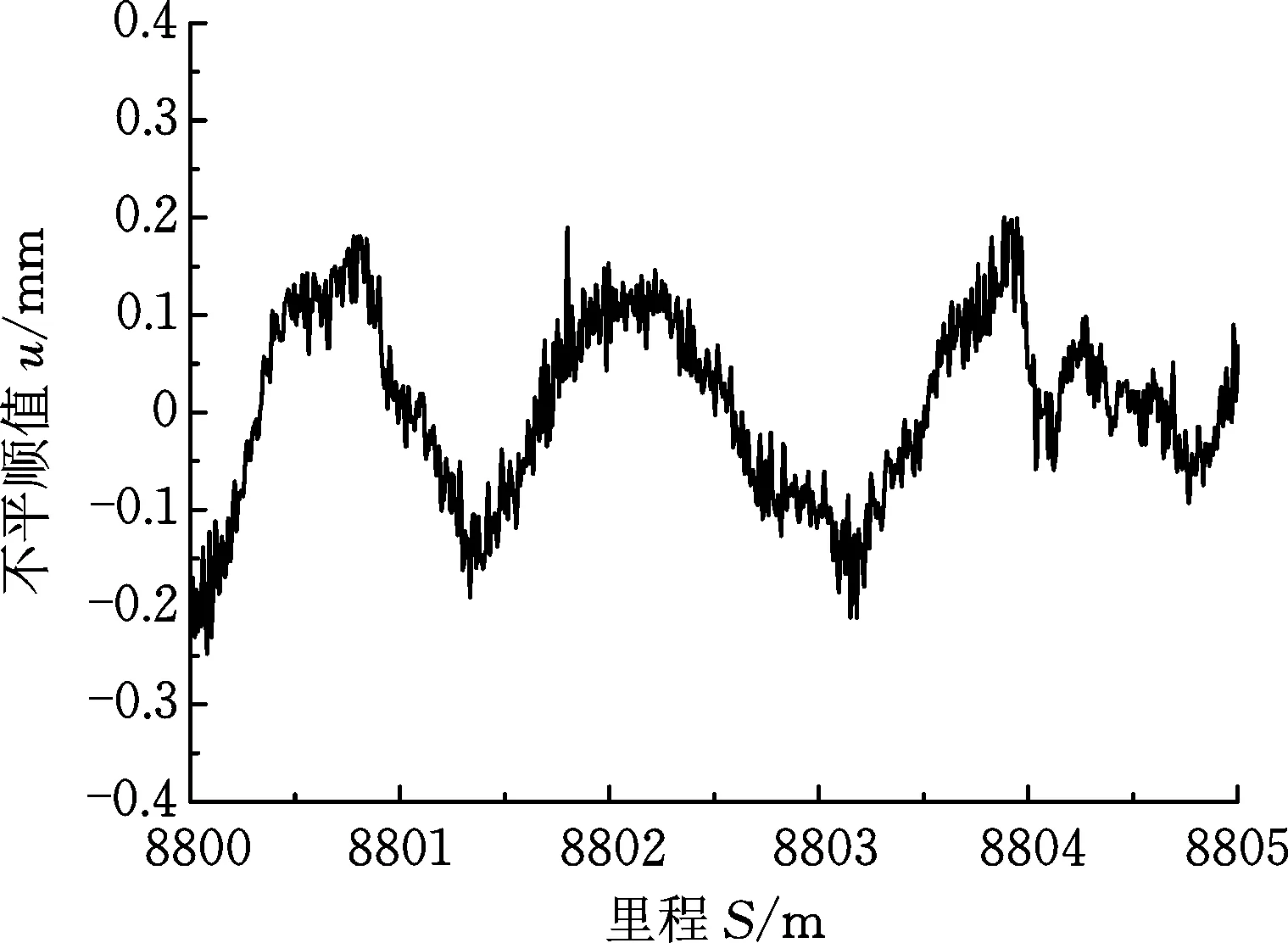
(b) 波磨不平顺
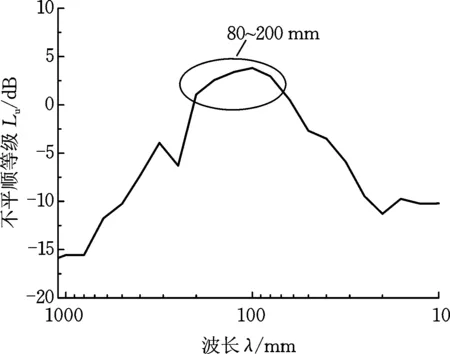
(c) 不平顺等级1/3倍频程波长图图4 实测波磨Fig.4 Measured corrugation
2.1 扣件纵向刚度
在保持其他控制变量不变的情况下,按照表3所示改变扣件纵向刚度,得到摩擦功率时程曲线和频谱曲线,如图5所示。

(a) 摩擦功率时程图
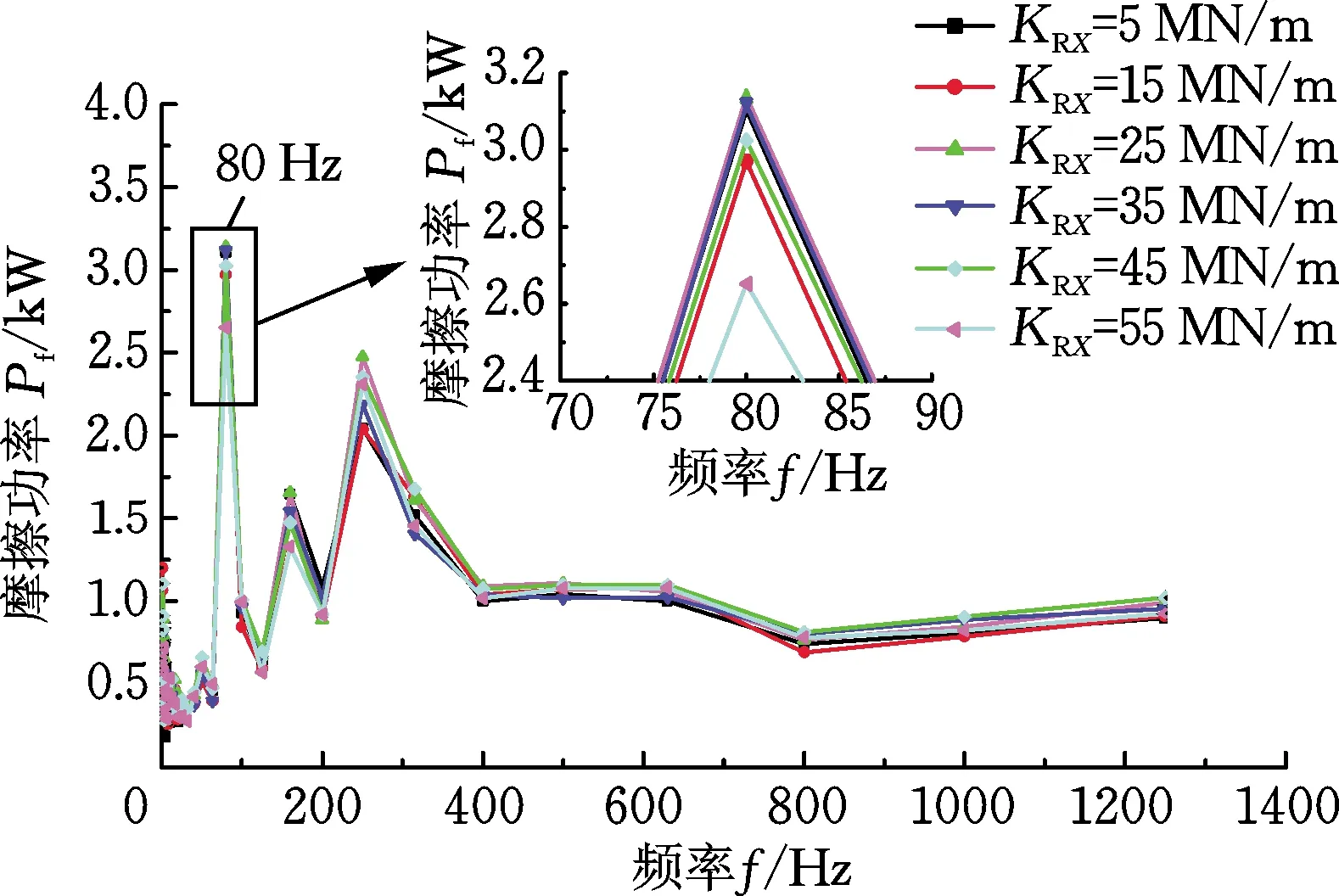
(b) 摩擦功率1/3倍频程图图5 改变扣件纵向刚度时的摩擦功率时频图Fig.5 Friction power time-frequency diagrams when changing the longitudinal stiffness of fasteners
由图5a可得,在不同的扣件纵向刚度下,轮轨接触斑内摩擦功率随时间的变化都具有一定的波动性,且摩擦功率整体波动幅度较为均匀。参考文献[30]可知,对于磨耗型波磨而言,摩擦功率随时间的波动变化对钢轨波磨的形成具有重要的作用,因此,摩擦功率的时程变化特性可以在一定程度上反映波磨的变化过程与规律。由图5b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率80 Hz处,扣件纵向刚度为55 MN/m时对应的摩擦功率幅值最小,然后按照扣件纵向刚度分别为15 MN/m、45 MN/m、5 MN/m、35 MN/m和25 MN/m顺序摩擦功率幅值依次增大,且不同扣件纵向刚度所对应的主要特征频率处摩擦功率幅值相差不大,说明在主要特征频率处,扣件纵向刚度对钢轨波磨的影响不明显。同时,随着扣件纵向刚度的增大,摩擦功率的特征频率没有发生改变,表明扣件纵向刚度的变化不会对钢轨波磨的特征频率产生影响。
2.2 扣件横向刚度
在保持其他控制变量不变的情况下,按照表3所示改变扣件横向刚度,分析轮轨接触斑内摩擦功率的变化趋势,并对其作频域变换,研究固定频率处钢轨波磨的发生和发展程度,如图6所示。
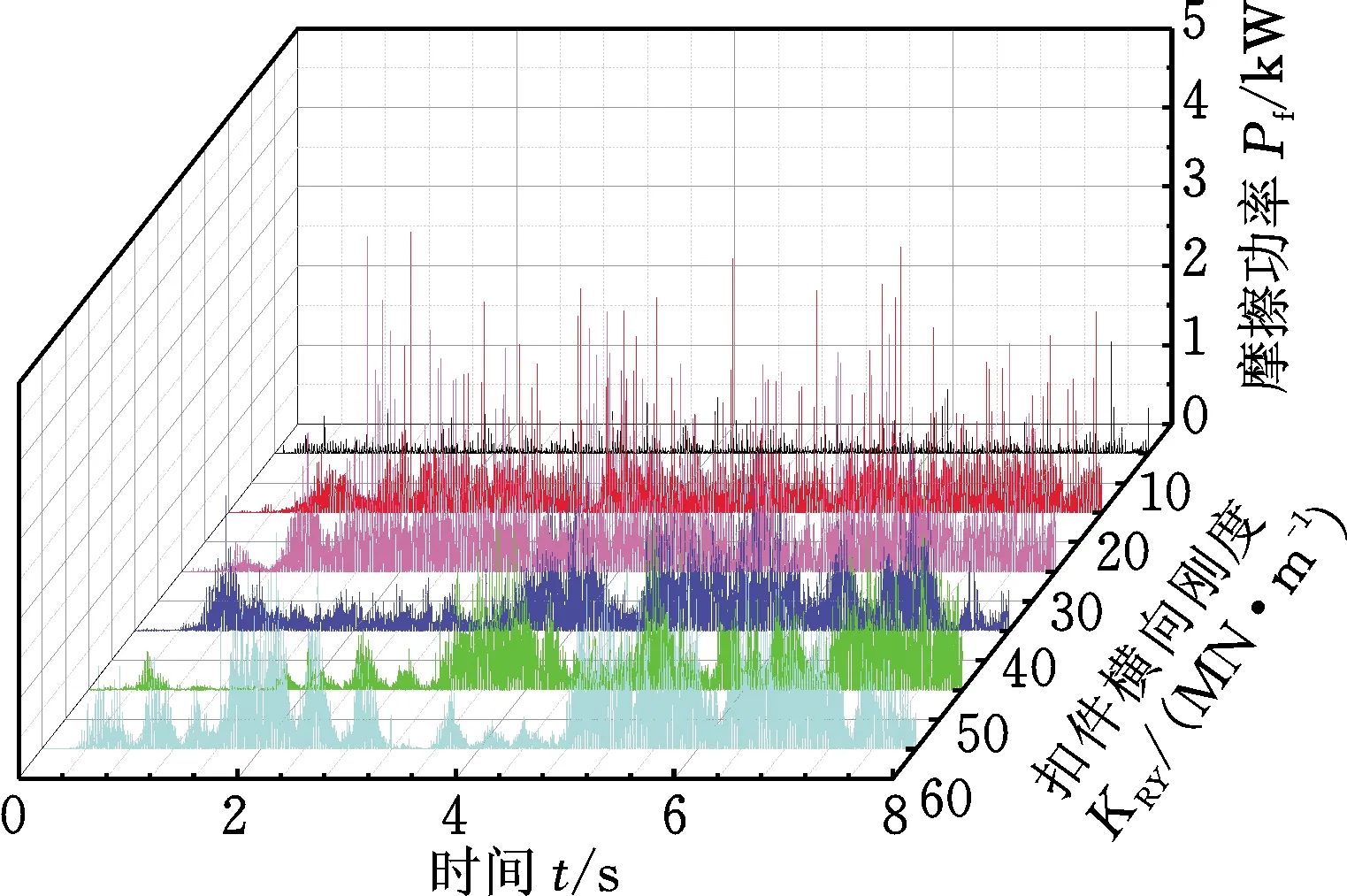
由图6a可得,在不同的扣件横向刚度下,轮轨接触斑内摩擦功率随时间的变化都具有一定的波动性,其中当扣件横向刚度为5 MN/m时,摩擦功率波动幅值较小。由图6b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率160 Hz处,扣件横向刚度为5 MN/m时对应的摩擦功率幅值最小,然后按照扣件纵向刚度分别为15 MN/m、25 MN/m、35 MN/m、45 MN/m和55 MN/m顺序摩擦功率幅值依次增大,尤其当扣件横向刚度为55 MN/m时,特征频率对应的摩擦功率幅值相对于其他扣件横向刚度值所对应的摩擦功率幅值而言大得多,说明在主要特征频率处,扣件横向刚度过大则不利于钢轨波磨的防治。同时,随着扣件横向刚度的增大,摩擦功率的特征频率几乎没有发生改变,表明扣件横向刚度的变化对钢轨波磨特征频率的影响较小。
(a) 摩擦功率时程图
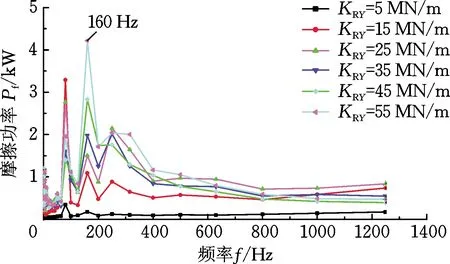
(b) 摩擦功率1/3倍频程图图6 改变扣件横向刚度时的摩擦功率时频图Fig.6 Friction power time-frequency diagrams when changing the transverse stiffness of fasteners
2.3 扣件垂向刚度
在保持其他控制变量不变的情况下,按照表3所示改变扣件垂向刚度,得到摩擦功率时程曲线和频谱曲线如图7所示。

(a) 摩擦功率时程图
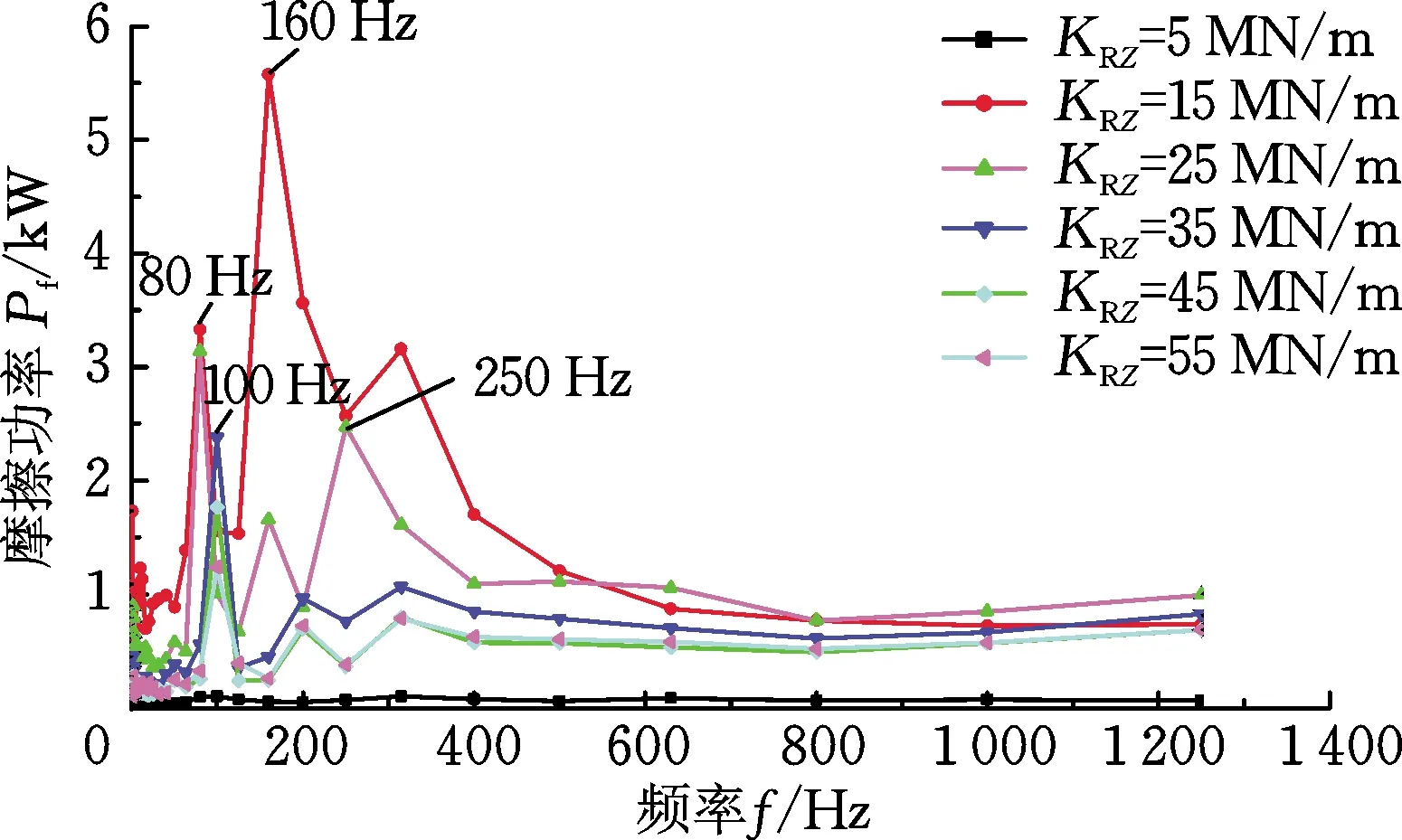
(b) 摩擦功率1/3倍频程图图7 改变扣件垂向刚度时的摩擦功率时频图Fig.7 Friction power time-frequency diagrams when changing the vertical stiffness of fasteners
由图7a可得,在不同的扣件垂向刚度下,轮轨接触斑内摩擦功率随时间的变化都具有一定的波动性,其中当扣件垂向刚度为5 MN/m时摩擦功率波动幅值较小。由图7b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在0~500 Hz范围内,扣件垂向刚度为15 MN/m时所对应的摩擦功率幅值较大,然后按照扣件垂向刚度分别为25 MN/m、35 MN/m、55 MN/m、45 MN/m和5 MN/m顺序摩擦功率幅值依次增大,其中扣件垂向刚度为55 MN/m和45 MN/m所对应的摩擦功率幅值相近;同时与扣件横向刚度和纵向刚度不同的是,扣件垂向刚度的变化会导致摩擦功率的特征频率发生偏移(如在低于125 Hz的频段内,扣件垂向刚度为35 MN/m、45 MN/m和55 MN/m所对应的主要特征频率相对于扣件垂向刚度为15 MN/m 和25 MN/m所对应的主要特征频率而言,从80 Hz偏移至100 Hz),从而导致对应波长的钢轨波磨,说明扣件垂向刚度对特定频率处钢轨波磨的产生和发展具有重要的影响。
2.4 扣件纵向阻尼
在保持其他控制变量不变的情况下,按照表3所示改变扣件纵向阻尼,得到摩擦功率时程曲线和频谱曲线如图8所示。

(a) 摩擦功率时程图
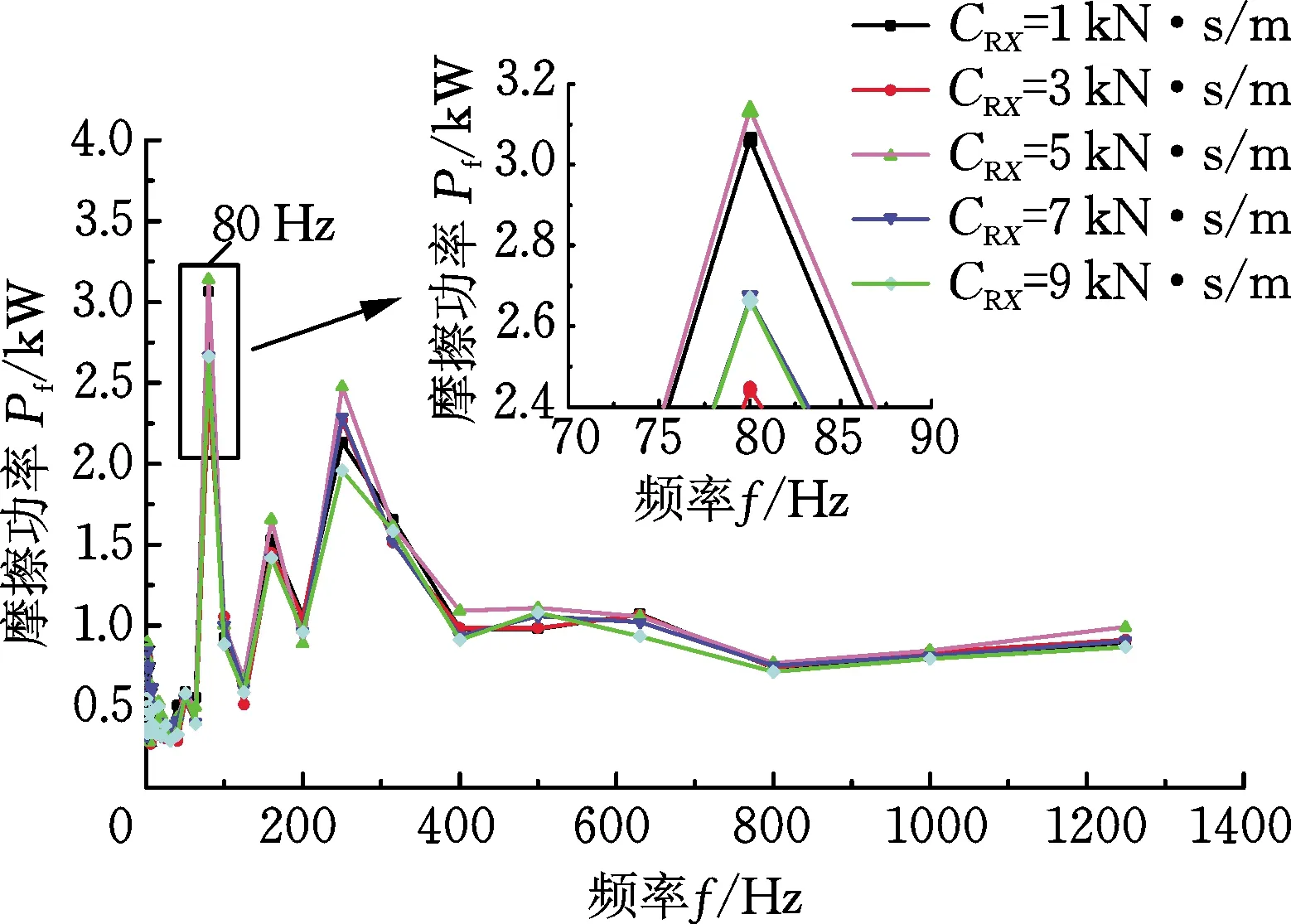
(b) 摩擦功率1/3倍频程图图8 改变扣件纵向阻尼时的摩擦功率时频图Fig.8 Friction power time-frequency diagrams when changing the longitudinal damping of fasteners
由图8a可得,在不同的扣件纵向阻尼下,轮轨接触斑内摩擦功率随时间的变化都具有一定的波动性,且摩擦功率整体波动幅度较为均匀。由图8b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率80 Hz处,扣件纵向阻尼3 kN·s/m对应的摩擦功率幅值最小,然后按照扣件纵向阻尼为9 kN·s/m、7 kN·s/m、1 kN·s/m和5 kN·s/m顺序,摩擦功率幅值依次增大,且不同扣件纵向阻尼所对应的主要特征频率处摩擦功率幅值相差不大,说明在主要特征频率处,扣件纵向阻尼对钢轨波磨的影响不明显。同时,随着扣件纵向阻尼的增大,摩擦功率的特征频率没有发生改变,表明扣件纵向阻尼的变化不会对钢轨波磨的特征频率产生影响。
2.5 扣件横向阻尼
在保持其他控制变量不变的情况下,按照表3所示改变扣件横向阻尼,得到摩擦功率时程曲线和频谱曲线如图9所示。
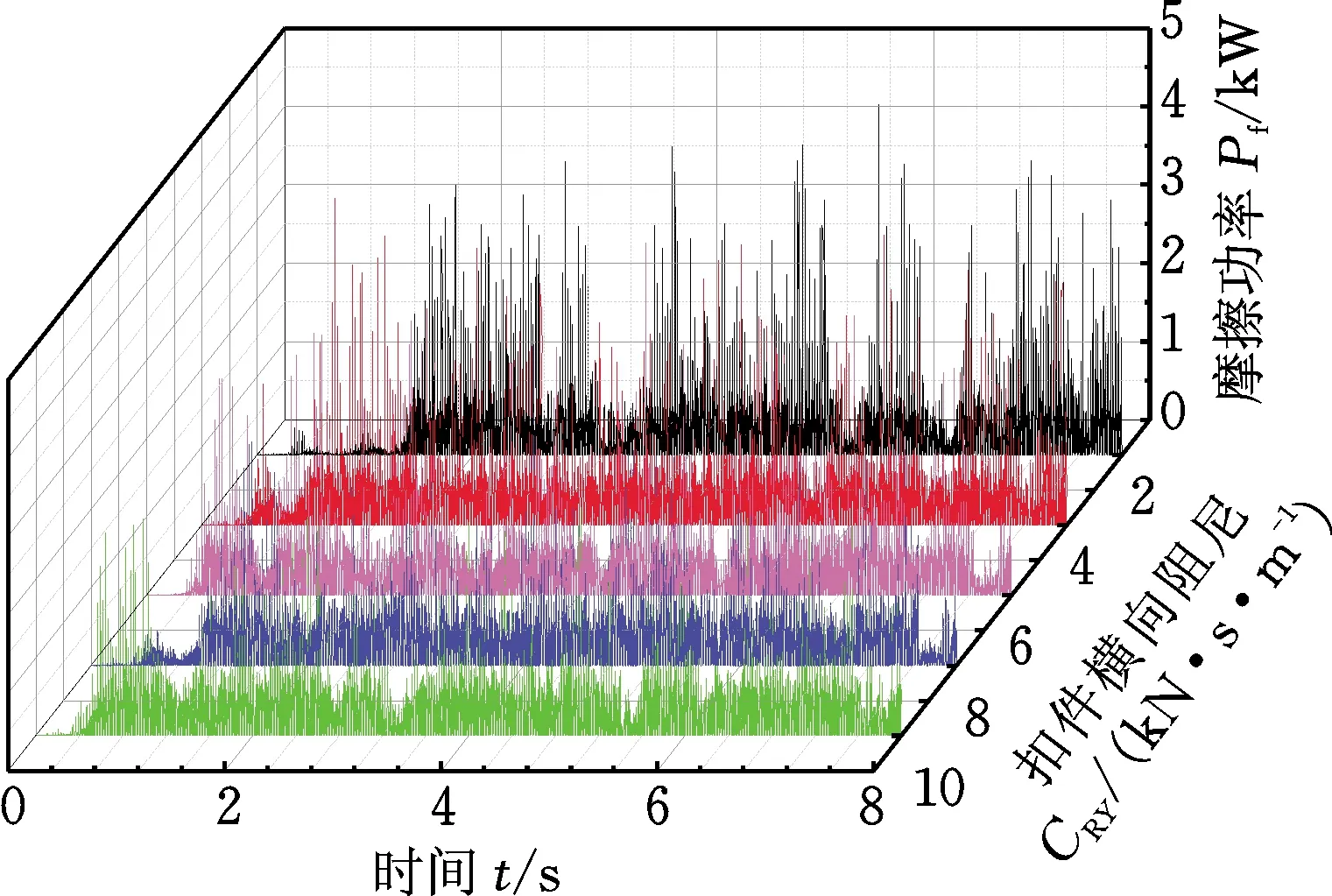
(a) 摩擦功率时程图

(b) 摩擦功率1/3倍频程图图9 改变扣件横向阻尼时的摩擦功率时频图Fig.9 Friction power time-frequency diagrams when changing the transverse damping of fasteners
由图9a可得,在不同的扣件横向阻尼下,轮轨接触斑内摩擦功率随时间的变化具有一定的波动性,且摩擦功率整体波动幅度较为均匀。由图9b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率80 Hz处,扣件横向阻尼为7 kN·s/m时对应的摩擦功率幅值最小,然后按照扣件横向阻尼为1 kN·s/m、9 kN·s/m、5 kN·s/m和3 kN·s/m顺序,摩擦功率幅值依次增大,且不同扣件横向阻尼所对应的主要特征频率处摩擦功率幅值相差不大,说明在主要特征频率处,扣件横向阻尼对钢轨波磨的影响不明显。同时,随着扣件横向阻尼的增大,摩擦功率的特征频率没有发生改变,表明扣件横向阻尼的变化不会对钢轨波磨的特征频率产生影响。
2.6 扣件垂向阻尼
在保持其他控制变量不变的情况下,按照表3所示改变扣件垂向阻尼,得到摩擦功率时程曲线和频谱曲线如图10所示。
由图10a可得,在不同的扣件垂向阻尼下,轮轨接触斑内摩擦功率随时间的变化具有一定的波动性,且摩擦功率整体波动幅度较为均匀。由图10b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率80 Hz处,扣件垂向阻尼为7 kN·s/m时对应的摩擦功率幅值最小,然后按照扣件垂向阻尼为5 kN·s/m、3 kN·s/m、1 kN·s/m和9 kN·s/m顺序,摩擦功率幅值依次增大,且不同扣件垂向阻尼所对应的主要特征频率处摩擦功率幅值相差不大,说明在主要特征频率处,扣件垂向阻尼对钢轨波磨的影响不明显。同时,随着扣件垂向阻尼的增大,摩擦功率的特征频率没有发生改变,表明扣件垂向阻尼的变化不会对钢轨波磨的特征频率产生影响。

(a) 摩擦功率时程图
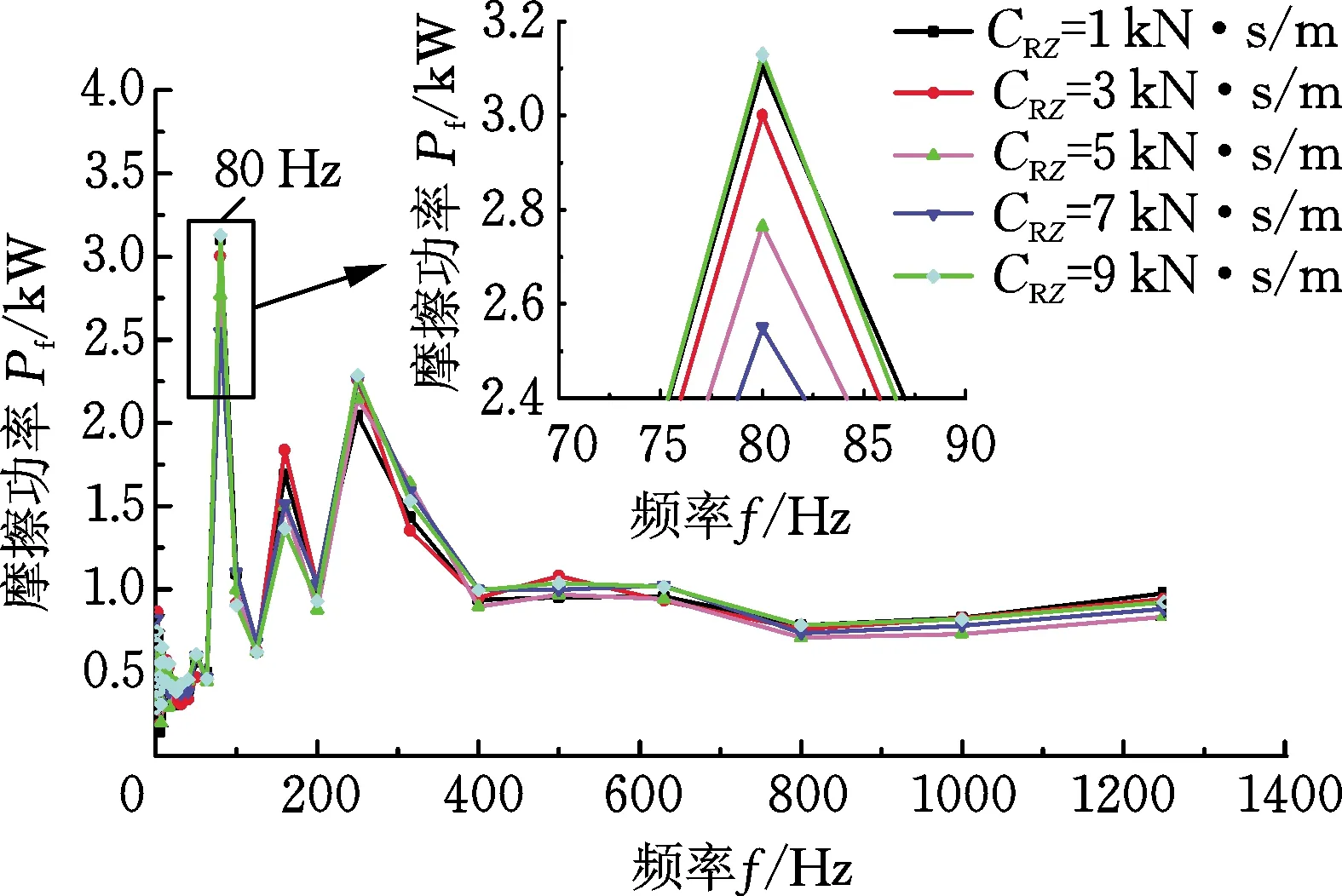
(b) 摩擦功率1/3倍频程图图10 改变扣件垂向阻尼时的摩擦功率时频图Fig.10 Friction power time-frequency diagrams when changing the vertical damping of fasteners
2.7 扣件间距
在保持其他控制变量不变的情况下,按照表3所示改变扣件间距,得到摩擦功率时程曲线和频谱曲线如图11所示。
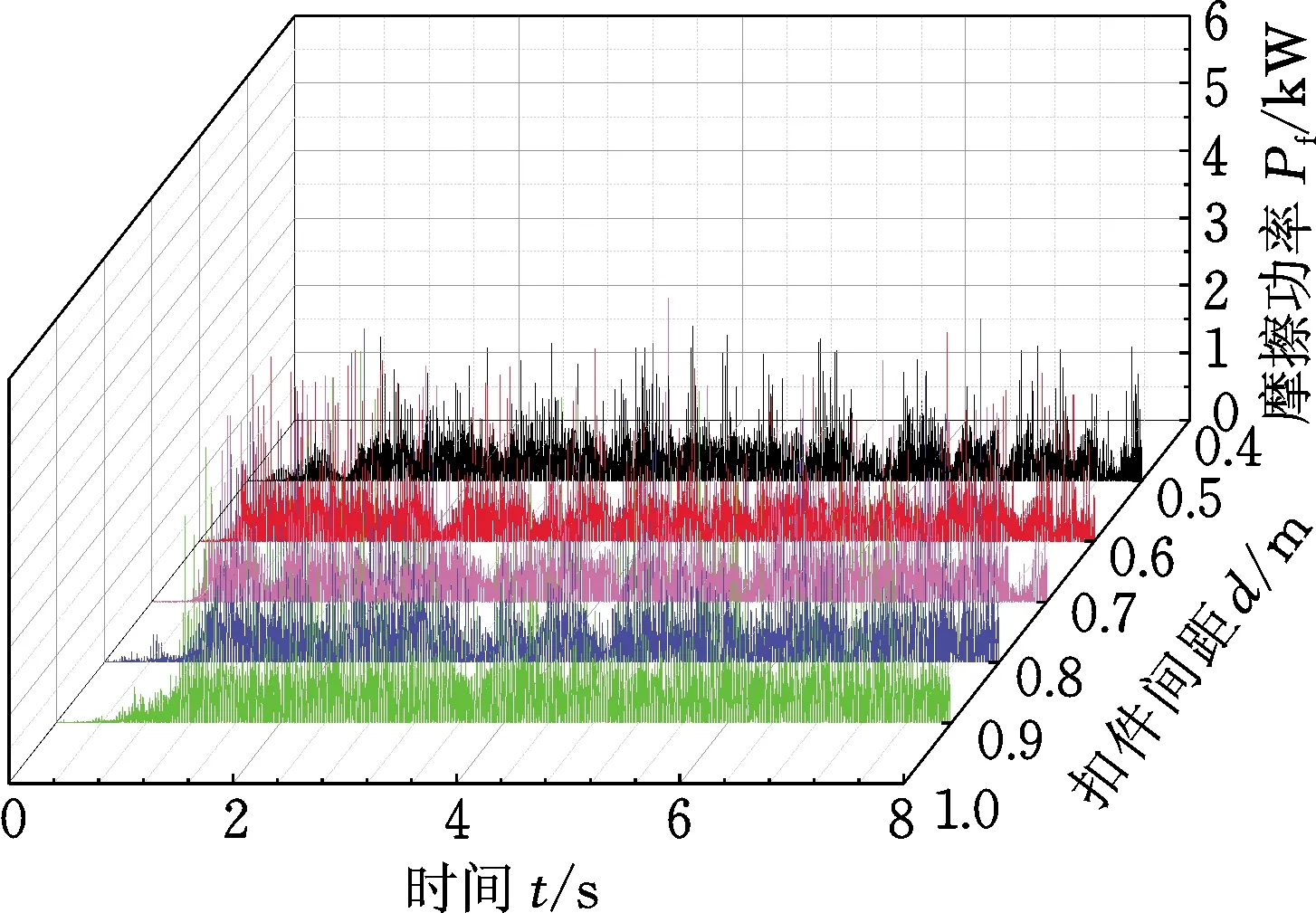
(a) 摩擦功率时程图
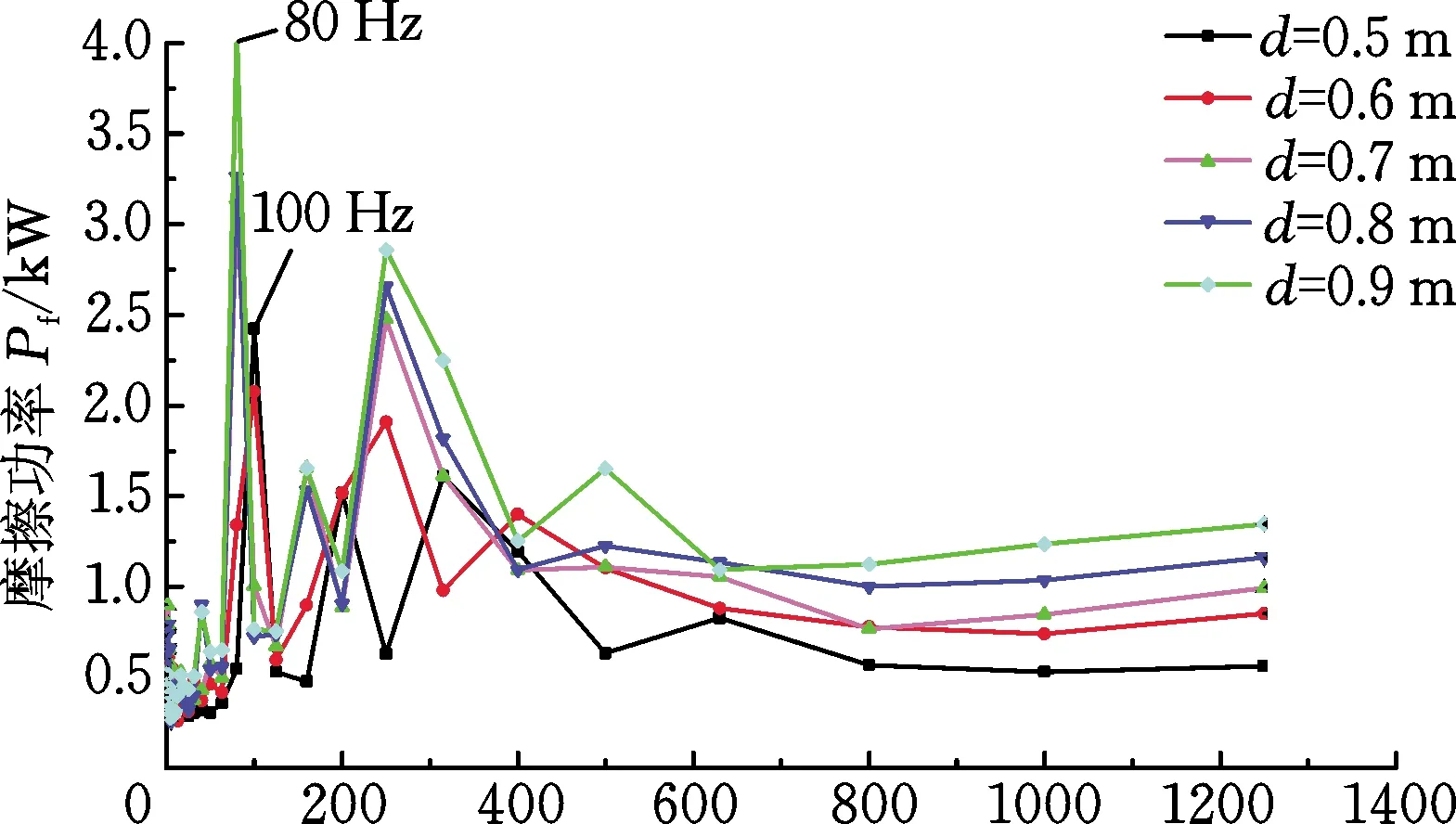
(b) 摩擦功率1/3倍频程图图11 改变扣件间距时的摩擦功率时频图Fig.11 Friction power time-frequency diagrams when changing the spacing of fasteners
由图11a可得,在不同的扣件间距下,轮轨接触斑内摩擦功率随时间的变化都具有一定的波动性,且摩擦功率整体波动幅度较为均匀。由图11b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在0~600 Hz范围内,扣件间距为0.6 m和0.5 m时所对应的摩擦功率幅值较小;扣件间距为0.9 m、0.8 m和0.7 m时所对应的摩擦功率幅值较大,且所对应的主要特征频率相对扣件间距0.6 m和0.5 m所对应的主要特征频率而言有所偏移(主要特征频率从80 Hz偏移至100 Hz),说明扣件间距对特定频率处钢轨波磨的产生和发展具有较大的影响。
2.8 轮轨摩擦因数
在保持其他控制变量不变的情况下,按照表3所示改变轮轨摩擦因数,得到摩擦功率时程曲线和频谱曲线如图12所示。
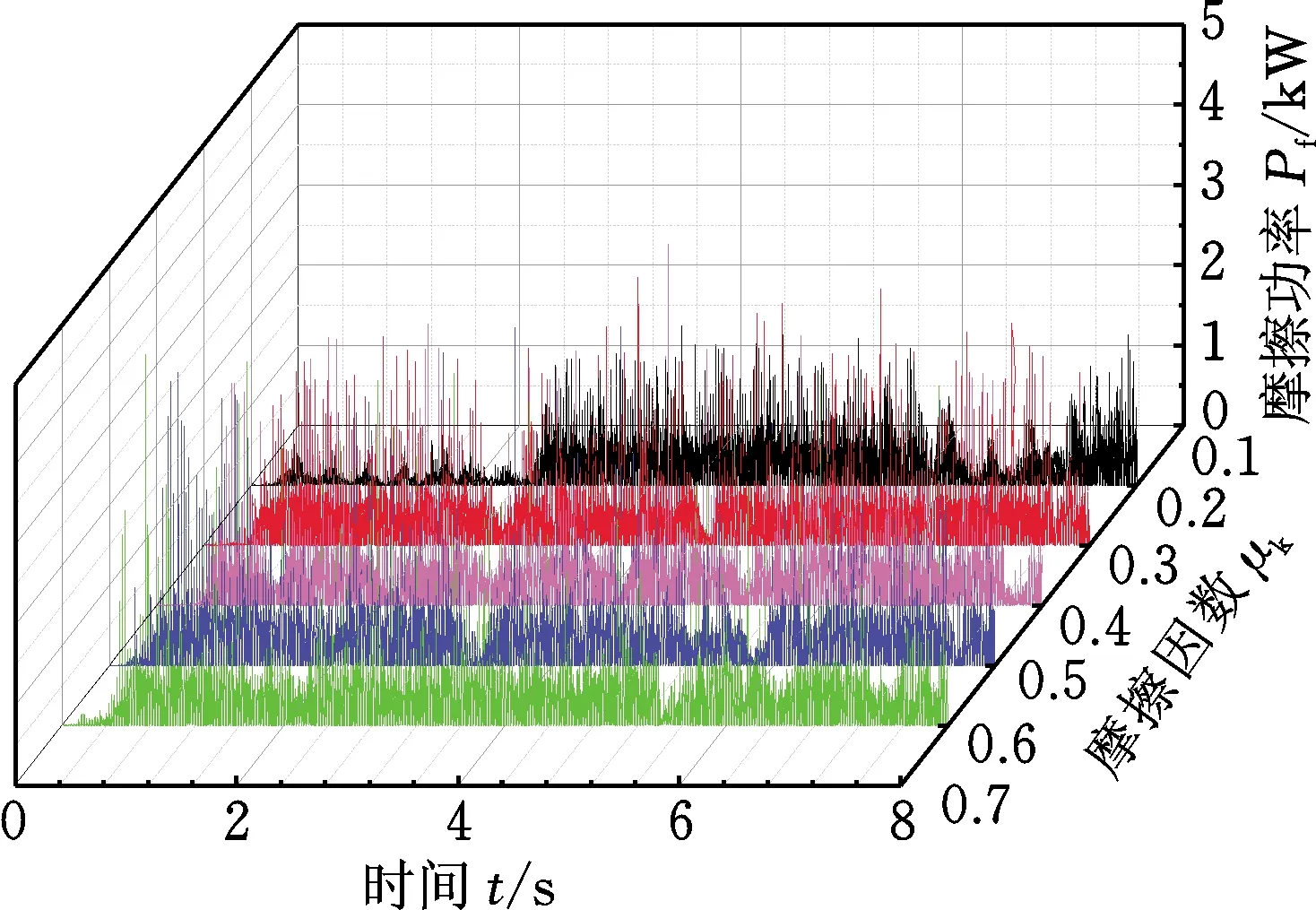
(a) 摩擦功率时程图
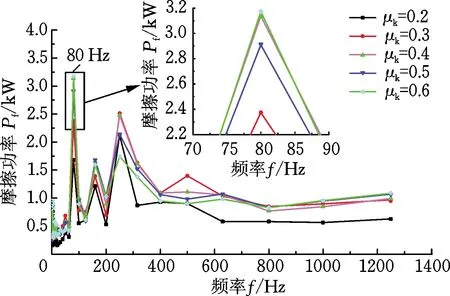
(b) 摩擦功率1/3倍频程图图12 改变轮轨摩擦因数时的摩擦功率时频图Fig.12 Friction power time-frequency diagrams when changing the wheel-rail friction coefficient
由图12a可得,在不同的摩擦因数下,轮轨接触斑内摩擦功率随时间的变化具有一定的波动性,且摩擦功率整体波动幅度较为均匀。由图12b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率80 Hz处,摩擦因数为0.2时对应的摩擦功率幅值最小,然后按照摩擦因数为0.3、0.5和0.4顺序,摩擦功率幅值依次增大,摩擦因数为0.6时对应的摩擦功率幅值最大。同时,随着摩擦因数的增大,摩擦功率的特征频率几乎没有发生改变,表明摩擦因数的变化对钢轨波磨特征频率的影响也相对较小。
3 车辆运行速度
本节主要分析车辆运行速度为40 km/h、50 km/h、60 km/h、70 km/h和80 km/h条件下,轮轨接触斑内摩擦功率的变化规律,同时对其进行频谱分析,研究不同频率处钢轨波磨的发生和发展情况。在保持其他控制变量不变的情况下,改变运行速度,作出摩擦功率的时程曲线图和频谱曲线图,见图13。
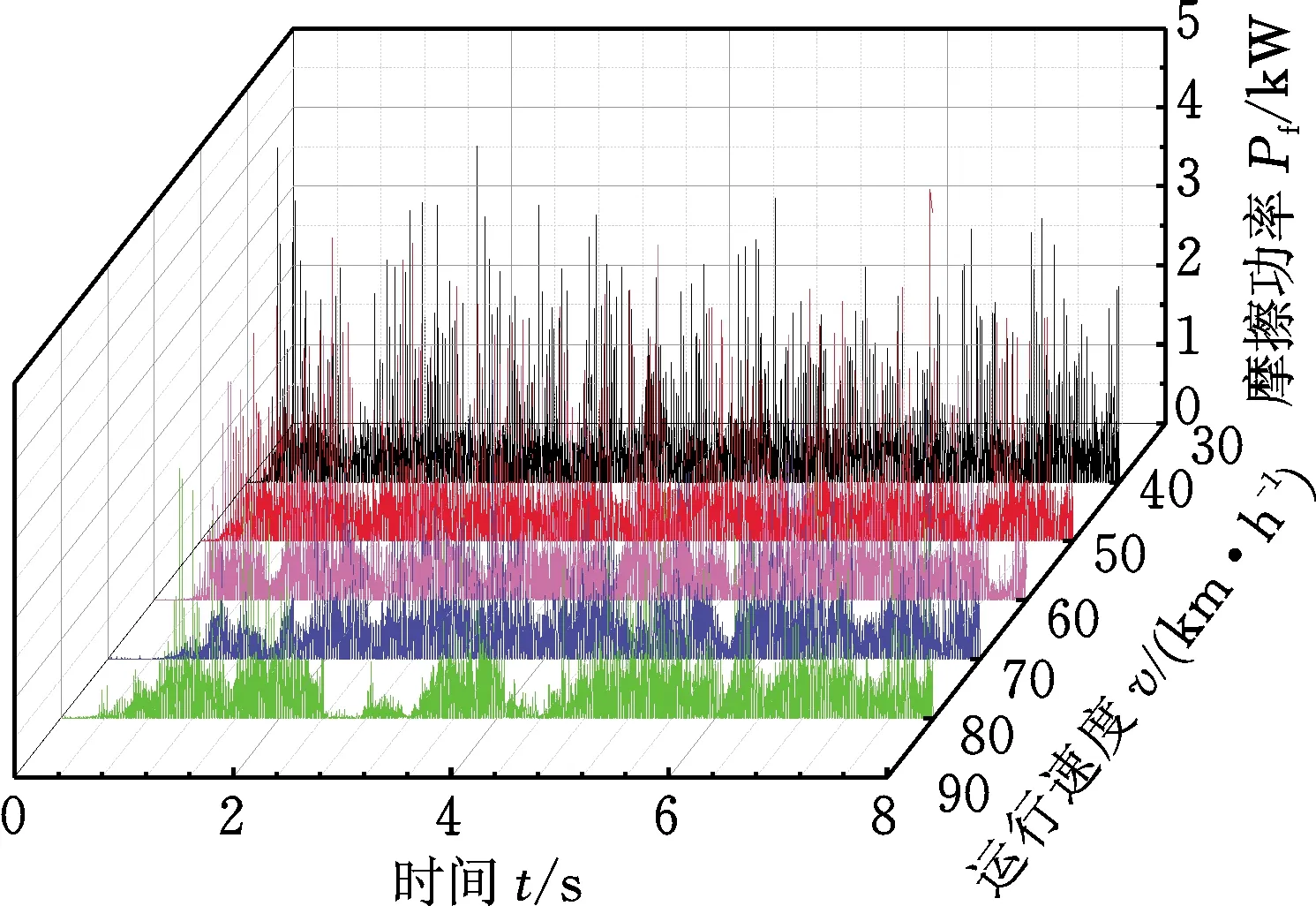
(a) 摩擦功率时程图
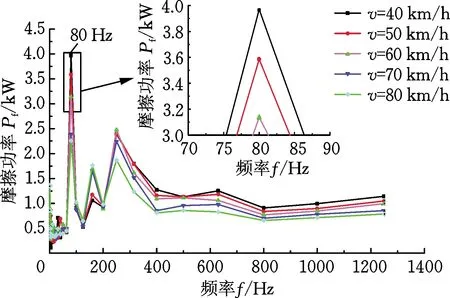
(b) 摩擦功率1/3倍频程图图13 改变车辆运行速度时的摩擦功率时频图Fig.13 Friction power time-frequency diagrams when changing the running speed of vehicles
由图13a可得,在不同的运行速度下,轮轨接触斑内摩擦功率随时间的变化具有一定的波动性,且摩擦功率整体波动幅度较为均匀。由图13b摩擦功率1/3倍频程图分析可知,摩擦功率的特征频率主要集中在中低频范围。在主要特征频率80 Hz处,运行速度为80 km/h时对应的摩擦功率幅值最小,然后按照运行速度为70 km/h、60 km/h和50 km/h的顺序,摩擦功率幅值逐渐增大。运行速度为40 km/h时对应的摩擦功率幅值最大。同时,随着运行速度的增大,摩擦功率的特征频率没有发生改变,表明运行速度的变化不会对钢轨波磨的特征频率产生影响。
综合图5~图13可知,特征频率为80 Hz处所对应的摩擦功率峰值均较大。分析认为,特征频率80 Hz为轮轨冲击的低频力所致。低频力可视为簧下质量与轨道作为整体质量在轨下弹性基础上的振动力,其频率范围为20~100 Hz,是由线路上不可避免的轨道不平顺以及车轮周向不圆顺引起的冲击力[31-32]。此外,特征频率160 Hz处所对应的摩擦功率峰值也较高。究其原因,对于1/3倍频程带宽而言,中心频率160 Hz所对应的频率范围为141~178 Hz,包含于初始不平顺所对应的通过频率范围为83~208 Hz,因此,可知钢轨表面初始不平顺是造成峰值频率160 Hz形成的主要原因。特征频率所对应的摩擦功率峰值越大,振动能量越高,钢轨磨耗也越大。依据波磨的固定频率特性可知,钢轨磨耗的加剧会进一步导致钢轨波磨的产生和发展。
4 结论
本文基于车辆-轨道耦合动力学模型和钢轨材料摩擦磨损计算模型,利用控制变量法,分析了不同轨道结构参数(扣件垂向刚度、扣件垂向阻尼、扣件横向刚度、扣件横向阻尼、扣件纵向刚度、扣件纵向阻尼、扣件间距以及轮轨摩擦因数)和车辆运行速度对直线轨道钢轨波磨发生和发展的影响,主要得到以下结论:
(1)对于不同的变量参数,轮轨接触斑内摩擦功率随时间的变化都具有一定的波动性,且摩擦功率整体波动幅度较为均匀。同时,摩擦功率1/3倍频程图分析结果表明,摩擦功率的特征频率主要集中在中低频范围。
(2)在主要特征频率处,扣件纵向刚度、扣件纵向阻尼、扣件横向阻尼和扣件垂向阻尼对钢轨波磨的影响较小,扣件横向刚度、扣件垂向刚度、扣件间距、轮轨摩擦因数和车辆运行速度对钢轨波磨的影响较大。
(3)扣件垂向刚度和扣件间距的变化会导致摩擦功率的特征频率发生偏移(主要特征频率从80 Hz偏移至100 Hz),从而导致对应波长的钢轨波磨,说明扣件垂向刚度和扣件间距对特定频率处钢轨波磨的产生和发展具有重要影响。其余变量的增大并未导致摩擦功率的特征频率发生改变,表明其余变量不影响钢轨波磨的特征频率。

