弹性车轮作用下低地板有轨电车轮轨磨耗研究
杨 阳 沈 健 王孔明 占 俊
1. 中铁二院工程集团有限责任公司科学技术研究院,成都,610031 2. 中铁第四勘察设计院集团有限公司,武汉,430063
0 引言
低地板有轨电车作为中等运量的城市轨道交通系统,具有造价远低于地铁系统、运量大于公交系统、线路条件灵活、环保节能等优点,是城市层次化公共交通体系的重要组成部分。截至2019年6月,中国大陆共有15座城市累计开通运营27条有轨电车线路,总里程355.33 km。
车辆在地面或高架的轨道上行驶时所产生的噪声会对周围居住生活环境造成一定的影响。随着生活品质的上升,城市居民对生活环境的要求越来越高,噪声问题变得日益突出。弹性车轮在轮箍与轮心之间安装有弹性橡胶元件,这使得轮箍相对于轮心变得更加柔软。弹性车轮能够有效地隔离振动和噪声,已在低地板有轨电车上得到广泛的应用[1-2]。
弹性车轮所使用的橡胶元件是一种非线性材料,因此对弹性车轮进行分析研究具有一定的难度。目前,有关弹性车轮的研究主要集中在减振降噪、轮轨动作用力、结构强度与疲劳方面[3-4],关于轮轨磨耗方面的研究报道较少。WEBER等[5]对使用弹性车轮的车辆的外场及车内噪声进行了分析,结果表明与使用刚性车轮的车辆相比,使用弹性车轮后车内噪声降低了3 dB,曲线尖啸噪声降低了8~10 dB。佐藤洁等[6-7]对弹性车轮的噪声进行了整车线路试验,对比25 m处的远场噪声降低了1~2 dB。在轮轨动作用力方面, ISHIDA等[8]分别将刚性轮对和弹性轮对单侧车轮抬起并进行落放试验,结果表明,弹性车轮与刚性车轮的动载荷之比约为0.8。丁军君等[9]利用Zorbory磨耗预测模型对弹性车轮作用下弹性车轮地铁车辆的车轮磨耗进行了分析,预测了弹性车轮的磨耗深度及镟修周期,并与使用刚性车轮的车辆进行了对比,结果表明,使用弹性车轮时车辆的镟修周期延长了27.8%。
目前,弹性车轮主要应用于低地板有轨电车,低地板有轨电车的车辆结构以及运行线路均与地铁有较大的差别。使用弹性车轮的地铁车辆踏面磨耗研究成果无法直接应用在有轨电车上,也未见学者们开展有关弹性车轮作用下低地板有轨电车轮轨磨耗方面的研究。本文基于Archard磨耗预测模型设计了使用弹性车轮的70%三模块低地板有轨电车车轮磨耗计算程序,研究了弹性车轮作用下车轮及钢轨的磨耗情况。
1 轮轨磨耗计算模型
1.1 弹性车轮结构
1950年美国人Herschfeld 发明了第一个可以用于商业运营的弹性车轮,随后弹性车轮得到了不断的发展与完善。在弹性车轮的发展历程中,按弹性车轮结构形式的不同可将其分为压缩型、剪切型和压剪复合型三种类型。压剪复合型弹性车轮的橡胶元件采用V形橡胶块,如图1所示,该弹性车轮能够同时承担径向和轴向载荷,可以通过改变V形的角度来合理匹配弹性车轮的径向和轴向刚度,使车辆具有较好的动力学性能。

图1 弹性车轮结构图Fig.1 Structure of resilient wheel
弹性车轮轮心相对于轮箍有6个方向的刚度,分别为相对于x、y和z轴的移动刚度,以及绕x、y和z轴的转动刚度。x向移动刚度与z向移动刚度的大小相同,统称为径向刚度,y向移动刚度称为轴向刚度;绕x向转动刚度与绕z向转动刚度的大小相同,统称为偏转刚度,绕y方向的刚度称为扭转刚度。
本研究通过试验及仿真分析相结合的方式来获取弹性车轮的各向刚度[10]。首先通过压力试验机获得橡胶元件的载荷位移曲线,橡胶块及试验装置如图2所示。

图2 橡胶块参数试验装置Fig.2 Rubber block parameter test device
然后利用有限元分析软件ABAQUS建立上述试验装置的有限元模型,其中橡胶元件为一种典型的超弹性材料,与线性材料不同,其本构模型一般采用多项式形式的应变势能密度U来表征。本文橡胶材料的本构模型选用Mooney-Rivlin模型,其应变能密度函数如下:
(1)

通过改变有限元分析模型中C10、C01参数,可得到变形量与作用力曲线,并与试验结果进行对比,当C10=1.21、C01=0.23时橡胶元件的载荷位移曲线试验结果与非线性有限元分析结果具有较好的一致性,如图3所示。

图3 试验结果与非线性有限元分析结果对比Fig.3 Comparison of test and nolinear finite element analysis results
建立弹性车轮的有限元模型如图4所示,采用六面体实体单元离散。轮箍、轮心、压环和螺栓的单元类型均为C3D8R,划分单元数目分别为 44 016、37 686、29 769和252; 橡胶的单元类型为C3D8H非线性大变形单元,橡胶块的单元数目为 760。

图4 弹性车轮有限元模型Fig.4 Finite element model of resilient wheel
根据图4所示的有限元模型得到弹性车轮各向载荷-位移曲线,并将线性化处理后的弹性车轮各向刚度汇总于表1。

表1 弹性车轮等效刚度Tab.1 Equivalent stiffness of resilient wheel
1.2 车辆动力学模型
以国内自主设计的70%低地板有轨电车为研究对象,该车辆采用三编组形式,如图5所示。两端为动力车、中间为拖车,动车与拖车之间采用固定铰、转动铰及自由铰连接,使其形成静定结构。

(a) 车辆结构形式

(b) 车辆原型图5 低地板有轨电车Fig.5 Low floor tram
车辆动力及非动力转向架的结构形式如图6所示,转向架采用轴箱外置的结构形式,一系采用锥型橡胶堆,二系采用沙漏簧,并设置二系横向减振器。

(a) 动力转向架

(b) 非动力转向架图6 转向架结构形式Fig.6 Bogie structure type
低地板有轨电车目前没有标准踏面形式,车辆采用为其设计的非标准踏面,轨道采用59R2槽型轨,轮轨接触关系如图7所示,可以看出,接触点分布均匀,接触状态良好。

图7 轮轨接触关系Fig.7 Wheel rail contact relationship
由于弹性车轮采用橡胶元件,弹性车轮动力学模型与刚性车辆动力学模型具有较大区别,因此在多体动力学分析软件SIMPACK中建立弹性车轮六自由度复合模型,其拓扑关系及建模方法如图8所示。其中,kx、ky、kz分别为沿x、y、z轴的移动刚度,kα、kβ、kγ分别为绕x、y、z轴的转动刚度。轮心和轮毂相互独立,通过力元模拟橡胶元件的刚度特性。每个轮毂与车轴之间均有一个绕y向旋转的自由度,并设置对应的扭转刚度。

图8 弹性车轮六自由度复合模型拓扑图Fig.8 Topological diagram of resilient wheel 6-DOF composite model
1.3 轮轨磨耗计算程序
机车车辆轮轨磨耗预测常应用的计算模型有Archard磨耗模型、Zobory磨耗模型、Specht磨耗模型。其中Archard磨耗模最为常用,在轮轨磨耗预测计算时取得了良好的效果[11-12]。故本文选用Archard磨耗模型计算机车车轮磨耗。
Archard磨耗模型认为[13],磨耗量与材料的表面硬度成反比,与摩擦行程以及法向载荷成正比。根据Archard磨耗模型进行轮轨磨耗计算时,车轮接触斑内任一单元(i,j)内的磨耗量可表示为
(2)
式中,KJ为Archard磨耗系数,与轮轨接触点的接触压力及滑动速度相关;pz为轮轨接触斑内相应单元的法向应力,MPa;Δl为单元的滑动距离,m;H为材料的布氏硬度,HBW。
车轮磨耗计算程序如图9所示,根据给定线路条件下车辆-钢轨耦合动力学模型,得到轮轨接触斑内每个单元的应力、滑动距离等数据,根据Archard磨耗预测模型计算接触斑内每个单元的磨耗量,并累积到车轮踏面上。磨耗分析过程中踏面更新策略受磨耗精度影响较大,为得到较为精确的计算结果,本研究将磨耗深度达到0.1 mm作为踏面更新条件[14-15],即当踏面的磨耗深度达到限值时对磨耗的踏面进行更新,用更新后的踏面再进行动力学计算,并用新的动力学计算结果进行磨耗分析。

图9 车轮磨耗仿真计算程序Fig.9 Wheel wear simulation program
钢轨磨耗计算模型与车轮磨耗计算程序类似,即计算接触斑内钢轨上每个单元的磨耗量,并累积到钢轨外形上。钢轨磨耗计算模型与车轮磨耗模型的不同之处在于统计磨耗量时不再是根据车辆运行里程,而是依据车辆通过次数,在计算过程中使车辆在某一段钢轨上行驶,钢轨磨耗量为车辆多次通过这一段线路的平均磨耗量[16]。
2 车轮踏面磨耗
2.1 轨道不平顺对车轮磨耗的影响
轮轨动作用力是影响车轮磨耗的重要因素,而轨道不平顺会直接影响轮轨作用力的大小。本文对使用弹性车轮及刚性车轮的车辆在美国Ⅴ、Ⅵ级谱的线路上运行时车轮的磨耗情况进行了研究。将车辆一位轮对作为研究对象,车轮运行速度为80 km/h,运行工况为直线工况。
当车辆在美国Ⅴ级谱工况下运行13.85万km后,车轮磨耗情况如图10a所示,可以看出:弹性车轮和刚性车轮的最大累积磨耗量分别为0.982 mm和1.083 mm,弹性车轮较刚性车轮的最大累积磨耗量减小了9.32%;弹性车轮和刚性车轮的累积磨耗截面面积分别为36.57 mm2和43.75 mm2,弹性车轮较刚性车轮的累积磨耗截面面积减小了16.41%。
当车辆在美国Ⅵ级谱工况下运行17万km后,车轮磨耗情况如图10b所示,可以看出:弹性车轮和刚性车轮的最大累积磨耗量分别为0.518 mm和0.584 mm,弹性车轮较刚性车轮的最大累积磨耗量减小了11.3 %;弹性车轮和刚性车轮的累积磨耗截面面积分别为21.49 mm2和23.50 mm2,弹性车轮较刚性车轮的累积磨耗截面面积减小了8.6%。

(a) Ⅴ级谱

(b) Ⅵ级谱图10 不同轨道不平顺条件下车轮累积磨耗量Fig.10 Wheel cumulative wear under different track irregularity conditions
车轮累积磨耗截面面积更能反映整个车轮的实际材料去除量。由图10可知,在美国Ⅴ级谱工况及美国Ⅵ级谱工况下,与刚性车轮相比,弹性车轮的累积磨耗截面面积更小,因此,在线路较差的情况下弹性车轮具有更好的减磨效果。这主要是因为随着线路条件变差,车辆振动剧烈,弹性车轮可表现出更好的减振效果。
2.2 曲线半径对车轮磨耗的影响
小半径曲线是造成车轮磨耗的重要因素,本文研究了曲线半径分别为200 m和500 m时弹性车轮和刚性车轮的磨耗情况。
车辆在半径为200 m的曲线线路上运行1800 m后车轮磨耗情况如图11所示,可以看出,弹性车轮曲线外侧和内侧的最大累积磨耗量分别为2.81 mm和0.55 mm,刚性车轮曲线外侧和内侧的最大累积磨耗量分别为2.70 mm和0.53 mm,弹性车轮较刚性车轮曲线外侧和内侧的最大累积磨耗量分别减小了3.9%和3.6%。

(a) 曲线外侧车轮

(b) 曲线内侧车轮图11 200 m半径曲线下车轮累积磨耗Fig.11 Cumulative wear of wheel under 200 m radius curve
车辆在半径为500 m的曲线线路上运行1800 m后车轮磨耗情况如图12所示,可以看出,弹性车轮曲线外侧和内侧的最大累积磨耗量分别为0.76 mm和0.25 mm,刚性车轮曲线外侧和内侧的最大累积磨耗量分别为0.88 mm和0.26 mm,弹性车轮较刚性车轮曲线外侧和内侧的最大累积磨耗量分别减小了13.64%和3.85%。

(a) 曲线外侧车轮

(b) 曲线内侧车轮图12 500 m半径曲线下车轮累积磨耗Fig.12 Cumulative wear of wheel under 500 m radius curve
由上述分析可知,弹性车轮在曲线半径较小的线路上对磨耗的降低效果较小,这主要是因为在小半径曲线下曲线外侧车轮轮缘与钢轨发生紧靠,并且车辆运行速度较低,振动较小,弹性车轮的作用不明显。随着曲线半径的增大,车辆通过曲线线路时轮缘与钢轨逐渐不再接触,并且随着车辆运行速度的提高,车轮会发生一定程度的振动,弹性车轮具有良好的减振作用,从而降低了轮轨磨耗。对于曲线内侧车轮,不同曲线半径对磨耗的影响不大,这是由车辆通过曲线线路时曲线内侧车轮减载,轮轨垂向力本身较小造成的。
3 钢轨型面磨耗
3.1 直线工况
当车辆以80 km/h的速度、共计90万次通过一段轨道不平顺为Ⅵ级谱的线路时,钢轨磨耗后的轨面外形和平均累积磨耗情况如图13所示,可以看出,运行弹性车轮和刚性车轮时钢轨的最大累积磨耗量分别为0.71 mm和1.06 mm,运行弹性车轮时比运行刚性车轮时钢轨的最大累积磨耗量减小了33%。运行刚性车轮时钢轨磨耗在轨距角处最大,而运行弹性车轮时钢轨磨耗量在整个磨耗区域内的分布较为均匀,主要是因为弹性车轮在横向振动时当轮缘与钢轨贴靠振动,橡胶元件会起到一定的减振作用,减小了轮轨动作用力,从而减小了钢轨轨距角处的磨耗量。

(a) 钢轨型面

(b) 累积磨耗量图13 直线钢轨磨耗情况Fig.13 Wear of straight rail
3.2 曲线工况
车辆以50 km/h 的速度通过半径为500 m的曲线线路100万次时,外侧和内侧轨道的平均累积磨耗如图14和图15所示。对于曲线外侧轨道,磨耗量主要集中在轨距角处,这主要是由车辆通过曲线线路时在离心力的作用下车轮向曲线外侧偏移,车轮轮缘与钢轨轨距角处接触造成的。当轨面坐标点从轨距角向钢轨两侧移动时,钢轨磨耗量急剧减小。对比图14和图15可知,弹性车轮对曲线钢轨有一定的降磨效果。

(a) 累积磨耗量

(b) 钢轨型面图14 500 m曲线半径钢轨外侧磨耗Fig.14 Outer rail wear of 500 m curve radius

(a) 累积磨耗量
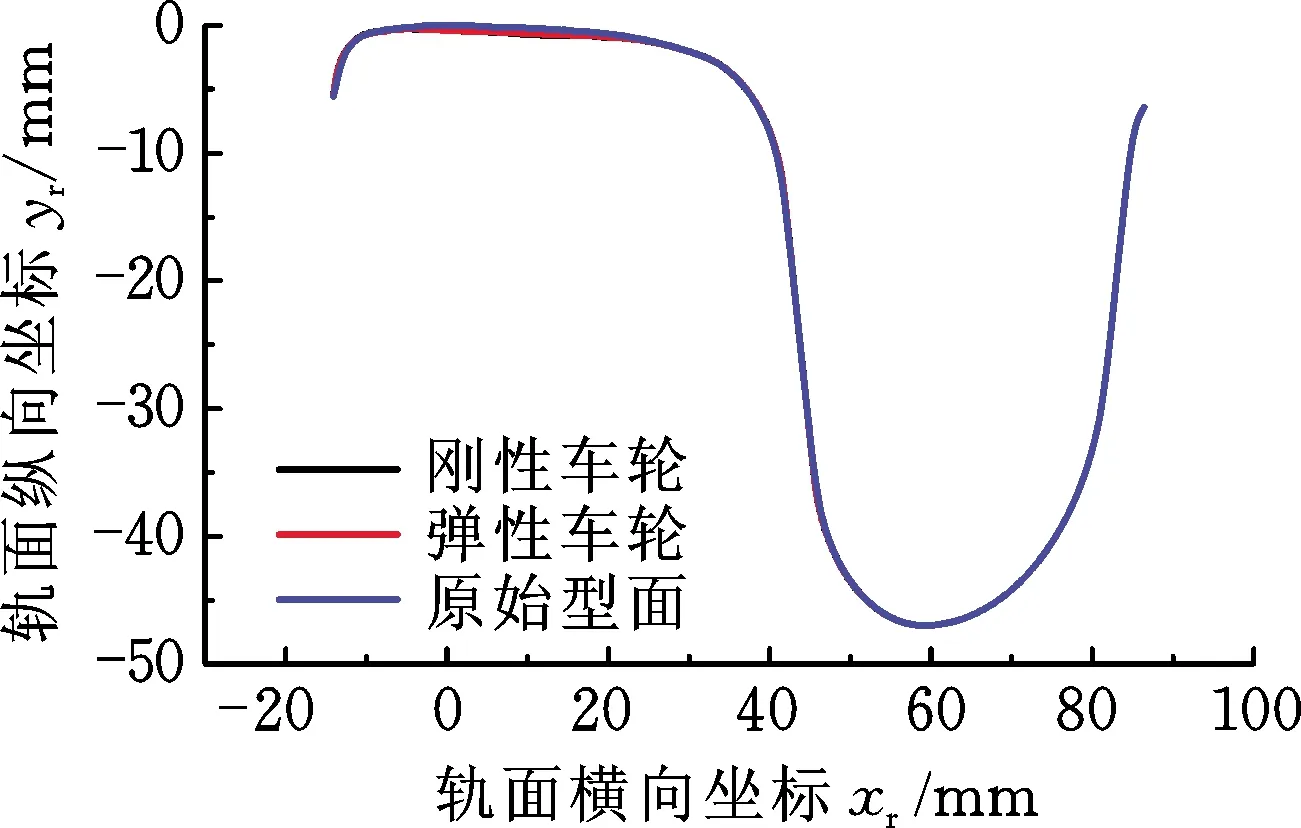
(b) 钢轨型面图15 500 m曲线半径钢轨内侧磨耗Fig.15 Inner wear of 500 m curve radius rail
4 结论
(1)车辆在美国Ⅴ级谱工况下运行时,弹性车轮比刚性车轮的累积磨耗截面面积减小了16.41%;在美国Ⅵ级谱工况下运行时,弹性车轮比刚性车轮的累积磨耗截面面积减小了8.6%;在线路较差的情况下弹性车轮具有更好的降磨效果。
(2)弹性车轮在曲线半径较小的线路上对磨耗的降低效果较小,随着曲线半径的增大,弹性车轮的减磨效果更加明显。
(3)运行弹性车轮时比运行刚性车轮时钢轨的最大累积磨耗量减小了33%。运行刚性车轮时钢轨磨耗在轨距角处最大,运行弹性车轮时钢轨磨耗量的分布较为均匀。
(4)弹性车轮对曲线钢轨有一定的降磨效果,对于曲线外侧钢轨,磨耗量主要集中在轨距角处,当轨面坐标点从轨距角向钢轨两侧移动时,钢轨磨耗量急剧减小。

