基于分岔理论的永磁同步电机非确定参数混沌控制

李洋洋，戴 磊，张 懿，魏海峰，李垣江

(1. 江苏科技大学 电子信息学院，镇江 212003；2. 江苏舾普泰克自动化科技有限公司，镇江 212003)

0 引 言

永磁同步电机系统具有复杂的非线性行为，凭借着小的转动惯量、高的工作效率、快速的响应性能被广泛地应用于各种工业场合。因此,研究永磁同步电机运行系统的非线性动力特性就变得十分有意义。就永磁同步电机的非线性分岔行为来说，复杂的连续Hopf分岔运动行为会导致运行系统进入混沌状态，一般发生在电机正常运行情况下受到外界干扰，亦或是受到系统本身传动装置的某种影响，导致电机在高性能发展领域受到阻碍[1-2]。永磁同步电机运行中，表现为转速与转矩的间歇性振荡，控制性能不稳定及不规则的电磁噪声等无规则运动现象，都有可能是电机运行系统中的混沌运动行为，这些行为会严重影响电机系统的高性能运转，使系统的稳定性、安全性得不到保障[3-5]。电机系统运行时所造成的突发性病态现象，会严重影响负载系统运行，降低系统的工作效率，所以对永磁同步电机运行系统的这种复杂非线性行为进行研究具有非常重要的应用价值。

对于永磁同步电机系统中的分岔与混沌行为，国内外已有研究人员提出了许多分析和控制的方法。文献[6-8]引入线性变换定理，得到永磁同步电机的无量纲化数学模型，基于Lyapunov稳定性判据推导出了电机运行系统的Hopf分岔条件。文献[9-10]研究了d,q旋转坐标系下的永磁同步电机模型，发现系统参数的变化会直接影响到系统平衡点的运行轨迹，从而会影响到系统的稳定性能。文献[11-13]引入非线性系统的闭环稳定性控制理论，设计了一种误差反馈学习算法进行控制电机运行系统的混沌行为，实现了对系统误差的实时补偿，该方法从很大程度上提高了系统的跟踪性能。文献[14-16]基于反步法设计了全局有限时间控制器，但是控制器中的一些参数很难确定。文献[17-18]基于一般非线性系统的分岔理论，研究了电机系统的分岔特性，该文献运用模糊控制原理对电机系统的分岔行为进行了同步控制，但是模糊控制容易降低控制系统的精度。文献[19-20]以永磁同步电机是参数不确定的非线性系统为切入点，基于自适应控制律提出了一种参数不确定的永磁同步电机混沌控制策略，用于对系统的不确定参数进行在线修正。该文献从理论上利用李雅普诺夫稳定性定理证明了控制算法的正确性，后又通过仿真进一步证明了处于混沌状态的系统在加入该控制器后能够很快进入稳定状态。

本文基于分岔理论研究了永磁同步电机通向混沌的道路，针对永磁同步电机运行系统的参数不确定性，设计了一种自适应混沌控制器，实现对系统的不确定参数实时预估，最终达到有效地抑制系统的混沌行为。

1 永磁同步电机运行系统的混沌数学模型

对永磁同步电机的电压平衡方程和转矩平衡方程通过d,q轴坐标旋转变换，得到常用数学模型如下式：

(1)

式中:id，iq，ud，uq分别为直轴，交轴定子电流和电压；ω是转子角速度；Rs为定子电阻；Ld,Lq分别为直轴和交轴的定子电感；ψr为磁链系数；TL为外部扭矩；β是摩擦系数；J是转动惯量；p为极对数。

永磁同步电机不管是在不断电运行的情况下，即ud,uq,TL不全为0；还是在负载为0并突然断电的情况下，即ud=uq=TL=0，永磁同步电机运行系统都有可能发生混沌行为。而本文就第一种情况展开研究，特取永磁同步电机系统运行条件为ud≠0，uq=0，TL=0，且运行环境为均匀气隙，即Ld=Lq。对式(1)进行仿射变换和时间尺度变换，得到其无量纲模型：

(2)

式(2)中的γ和σ是不确定参数，已有文献证明在特定的参数条件下，永磁同步电机系统会产生混沌运动。若永磁同步电机系统在运行过程中由于某种干扰或其他因素产生混沌行为，这种混沌行为往往会使得系统产生不规则的电磁噪声，又或者造成突发性的病态机电振荡现象，并且对电机转子造成极大的破坏，减少电机的使用寿命。因此，本文就永磁同步电机在运行过程中产生的混沌行为进行分析并进行控制具有很大的研究意义。

2 永磁同步电机运行系统的分岔分析

ud≠ 0，uq= 0，TL=0，是指电机于空载状态运行，且只有d轴电压供电的情况下，从式(2)中可以得出系统的平衡点为O(ud，0，0)。其中，令[x1,x2,x3]=[id,iq,ω]，则其余两个非零平衡点由下列方程组决定：

求得系统两个非零平衡点：

(3)

本文就系统平衡点的稳定性展开分析系统的分岔行为，首先求解系统的雅克比矩阵：

(4)

根据系统的雅可比矩阵求解特征多项式：

L(λ)=λ3+(σ+2)λ2+

(1) 当平衡点为O(ud，0，0)时，代入特征多项式：

L(λ)=λ3+(σ+2)λ2+

(σud+2σ+1-σγ)λ+

(ud+1-γ)σ

解得对应的特征值：

λ1=-1

① 当γ∈(0,ud+1)时，特征值全部为负数，所以平衡点O是稳定的；

② 当γ=ud+1时，有λ1=-1，λ2=-(σ+1),λ3=0时，即系统有一个零特征值，说明平衡点O附近还存在其他平衡点，则系统的拓扑结构发生了变化，即系统在此时出现了分岔现象；

③ 当γ>ud+1时，系统有两个负的特征值λ1、λ2和一个正的特征值λ3，此时平衡点O成为鞍点，且系统不再稳定。

综合①②③可知，系统在γ=ud+1时发生叉形分岔，此时，平衡点O由稳定变为不稳定，并且将出现新的平衡点X1和X2。

(2) 针对于非零平衡点，由于X1和X2严格对称，本文只分析其中一个，就平衡点X1作为研究对象进行分析。由式(3)和式(4)可得系统对应于平衡点X1的特征式：

L(λ)=λ3+(σ+2)λ2+(γ+σ-ud)λ+

2(γ-1-ud)σ

由Hopf分岔判定定理得在平衡点X1处产生Hopf分岔的临界条件：

(5)

即当γ=γ0时，系统状态变量id，iq，ω将产生Hopf分岔；当γ>γ0且γ继续变化，系统状态变量id，iq，ω将通过产生连续的Hopf分岔最终进入混沌状态，即永磁同步电机运行系统将会产生不规则的电磁噪声，甚至有可能造成突发性的电机故障。

系统参数σ取18.24，ud取2.56，可求得系统静态分岔参数γ=3.56，Hopf分岔参数γ0≈24.66，为了方便分析系统平衡点的分岔现象，取状态变量x2，做出其随分岔参数变化的分岔图，如图1所示。

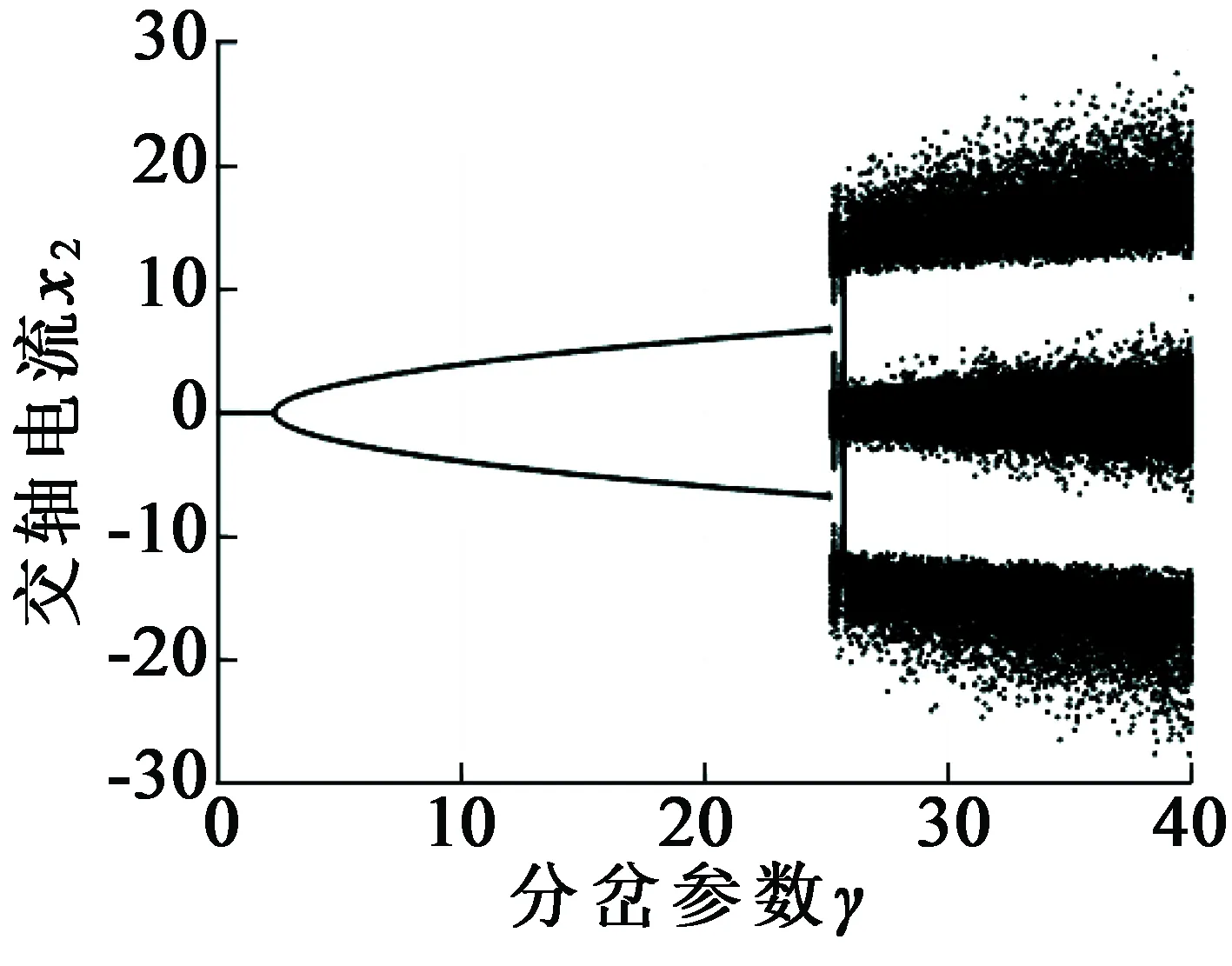
图1 系统分岔图

从图1中可以看出，系统在γ=3.56左右产生静态分岔，系统由一个平衡点变为两个平衡点；在γ=24.66左右产生了Hopf分岔，系统的平衡点逐渐稳定于一个极限环上；当γ>24.66时，系统的平衡点呈现出无规则的分布，此时系统进入混沌运行状态。分别取三组γ参数，γ1=2.2、γ2=16.6、γ3=28.4，做出不同的分岔参数下的系统相图。

永磁同步电机运行系统在工作过程中，随着分岔参数的变化，系统首先会产生静态分岔，即γ=ud+1，此时系统的平衡点将会变为两个新的平衡点，之前的平衡点将不再稳定，系统相图会体现为系统的平衡点收敛至一个点，即系统稳定；如图2所示，当分岔参数γ∈(0，24.66)时，系统的平衡点的轨迹稳定并且收敛，即永磁同步电机运行系统在此参数区间是稳定的。

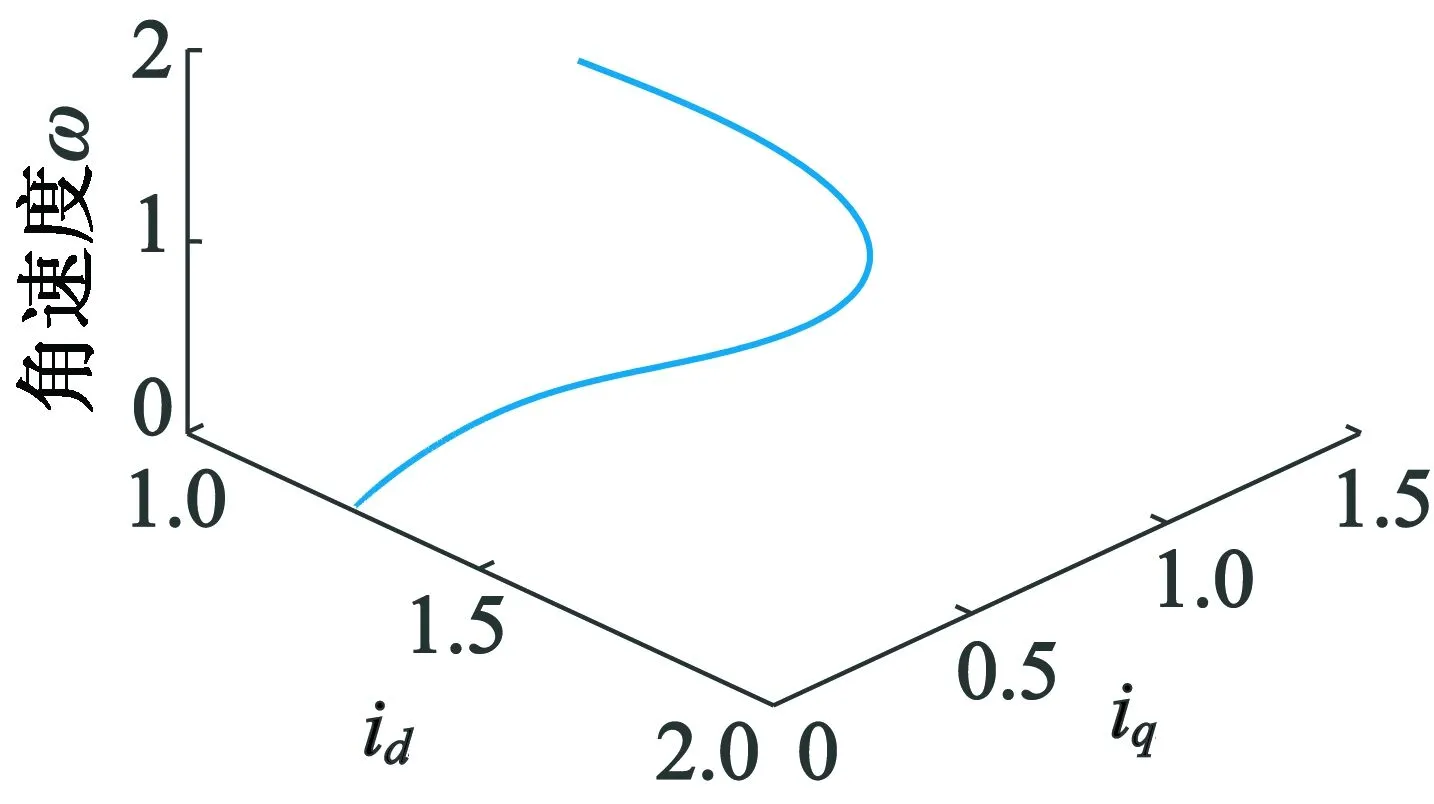
(a) γ1=2.2

当γ>ud+1时，系统会产生Hopf分岔，此时系统相图的拓扑结构发生变化，系统相图会体现为系统的平衡点将收敛到一个环上，而不再是收敛到点，此时的环称为极限环，同时系统的解会呈现周期性，显然此时的系统依然稳定，还未出现混沌现象。然而,随着系统分岔参数的继续变化，直至分岔参数突破某一临界点，系统平衡点稳定的环状结构将会被打破，最终系统平衡点将会无规则分布。

当参数γ>24.66时，随着γ的变化，系统平衡点的轨迹将不会始终稳定在极限环上，如图3所示。从图3中可以看出，系统的轨线从初始点(0,1,1)出发，先绕平衡点X1旋转再绕平衡点X2旋转，然后又绕平衡点X1旋转，但是轨线绕每个点旋转的圈数都是不确定的，具有随机性，这就形成了系统的奇怪吸引子。此时系统的解是无规则的，不再是稳定于极限环上的周期解，系统已经进入混沌运行状态，称此时的系统是混沌系统。

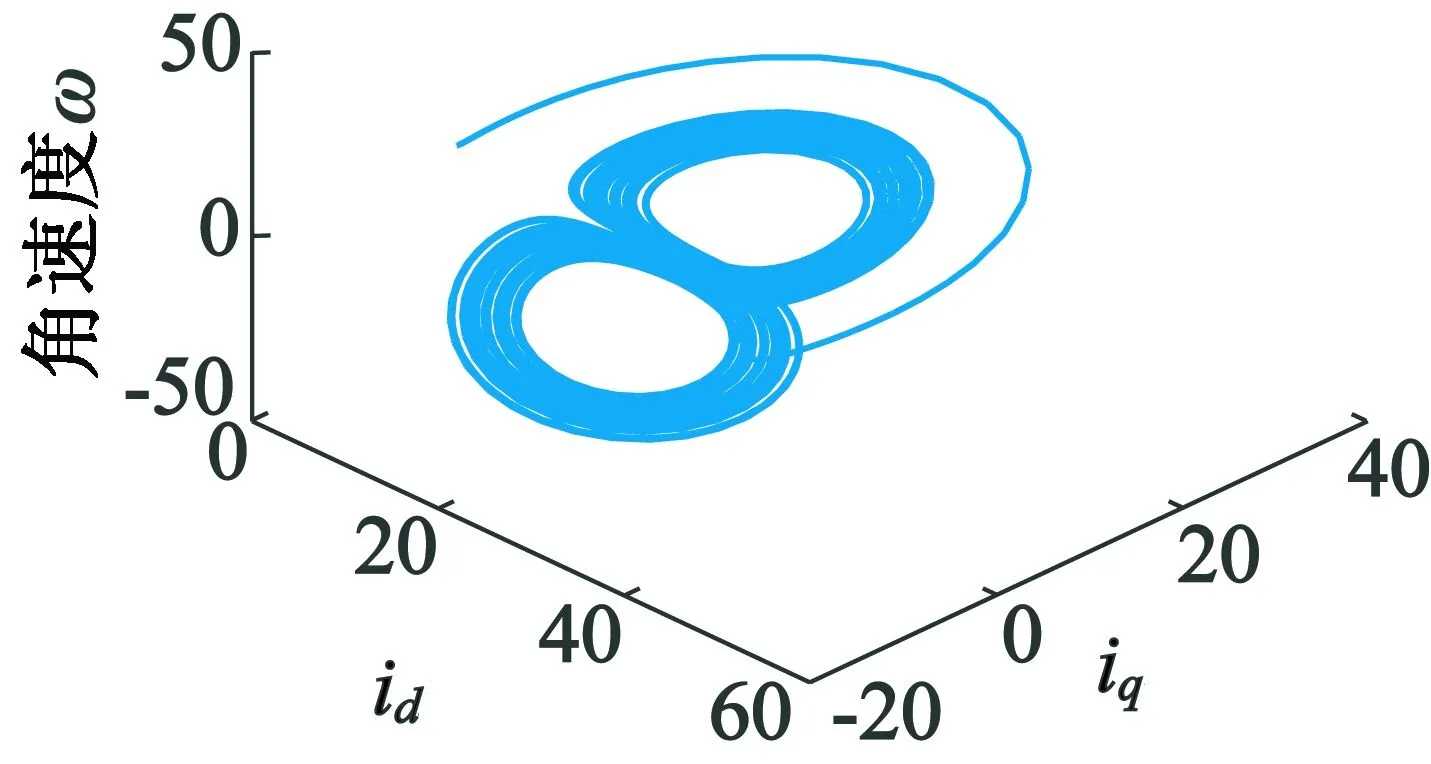
图3 γ3=28.4时的系统相图

3 永磁同步电机运行系统的混沌控制

上述对永磁同步电机一种参数情况下进行了分岔研究，分析得知当分岔参数大于临界值，即γ>24.66时，运行系统会进入混沌运行状态，即系统将不再稳定。为了仿真工作在混沌状态下的永磁同步电机运行系统，系统参数σ取18.24，分岔参数γ取28.4，对应图3，永磁同步电机运行系统工作在混沌状态下。由式(3)可得系统此时的平衡点X=(27.4，4.984，4.984)，为了有效控制这种混沌行为，本文基于自适应理论设计了混沌控制器，使得进入混沌状态的永磁同步电机运行系统最终稳定于平衡点。

本设计相对于文献[20]在控制器的数量上进行了优化，减少了控制器的数量，加入控制器后的系统模型：

(6)

系统中的控制器的推导如下，令：

u=-βsign(x2)|x2|k-γ0a-σ0b-c

式中:γ0，σ0分别为γ和σ的估计值；β为控制增益；a,b,c分别为设定的变量。

取Lyapunov函数V1：

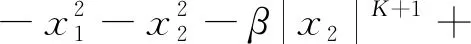
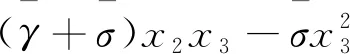
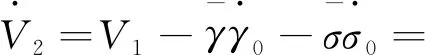
即系统的控制器：

根据Lyapunov稳定性定理可知，式(7)在加入控制器后是Lyapunov稳定的。

4 仿真分析

永磁同步电机是一种多参数系统，具有复杂的非线性行为，在实际的工程环境下，系统中的参数值是未知的，通常会因为外界的干扰导致参数的精确值很难得到，本文为了解决参数不确定问题，采用自适应控制方法来消除系统参数不确定的混沌问题，并取得了良好的控制效果。

本文在t=15时，对系统加入自适应控制器u，抑制系统的混沌行为。图4为加入控制器后的系统状态图。从图4中可以发现，在受外界因素影响，系统内部参数很难确定的情况下加入自适应控制器，能够有效地控制电机稳定运行，并且最终稳定到平衡点X=(27.4，4.984，4.984)。

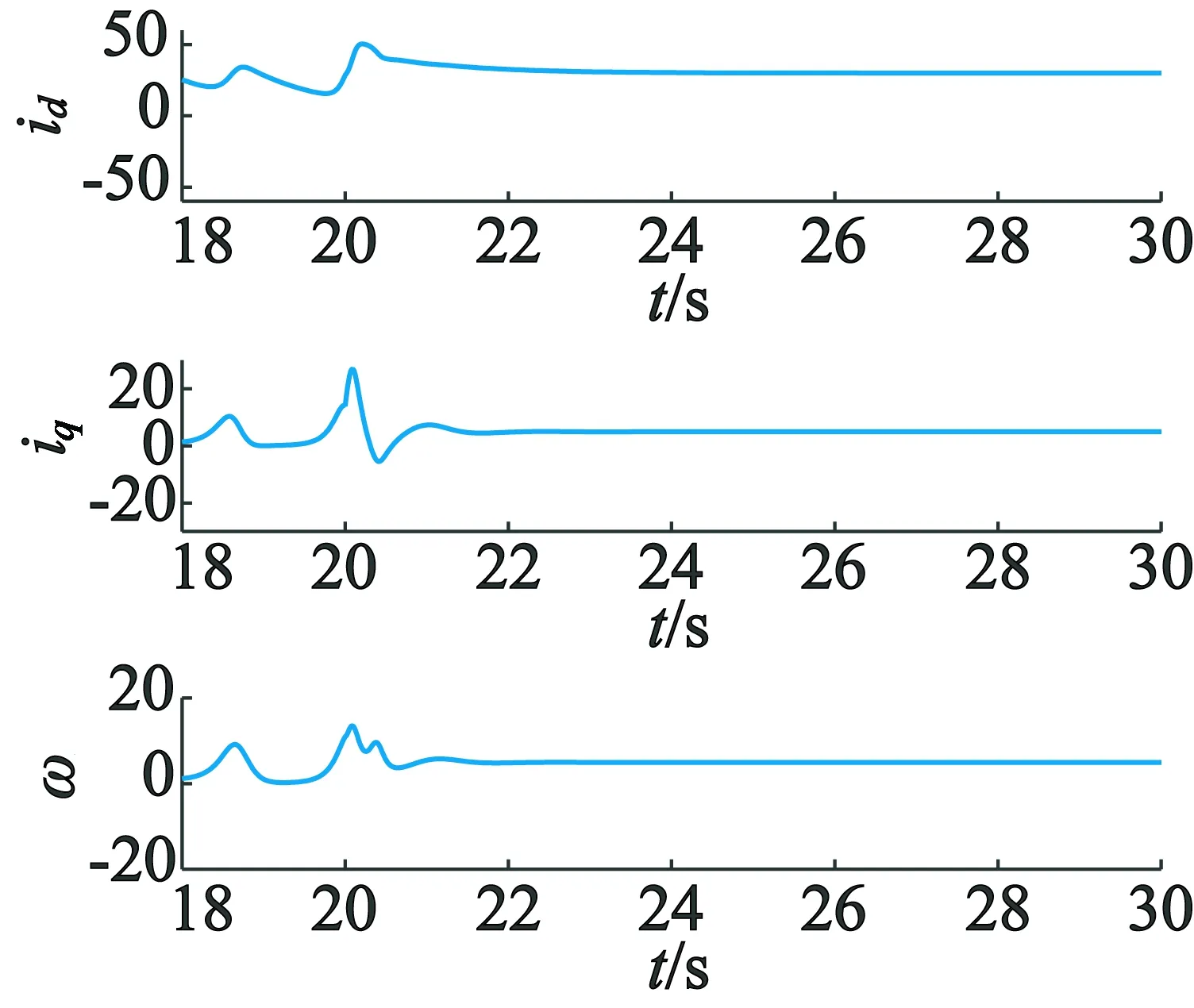
图4 加入控制后iq，id，ω的状态图

5 结 语

本文将永磁同步电机运行系统的物理模型进行时间尺度变换和线性仿射变换，得到一个无量纲化数学模型，减少了系统模型中的参数，方便了对系统状态的分析。

本文分析了系统平衡点的分岔特性，发现系统的静态分岔点和Hopf分岔点最终都与系统参数σ和ud有关。在仿真中，取σ=18.24，ud=2.56，计算得系统的静态分岔点为3.56，Hopf分岔点为24.66，随着分岔参数γ的继续增大，系统出现了连续的Hopf分岔现象，最终进入混沌状态。

为了有效地控制永磁同步电机系统的混沌行为，采用自适应控制算法，基于系统参数的不确定性设计了一种自适应混沌控制器。根据Lyapunov稳定性理论，证明了控制器的稳定性。通过MATLAB仿真，在t=20时加入控制器，仿真图表明，在加入控制器后，系统各个状态能够快速地进入稳定状态。