基于稳健卡尔曼滤波的倾斜探测电离层MUF短期预报方法

李国军，郑广发，叶昌荣，周银萍

（重庆邮电大学超视距可信信息传输研究所，重庆 400065）

1 引言

电离层是随时间、空间高度变化的复杂系统，它对短波天波的传播、地空和星间的信息链路有着至关重要的影响，是短波通信链路的中间介质。由于受太阳辐射、大气环流和地磁环境等多种因素的影响，电离层具有时变色散特性，容易发生扰动，影响短波通信质量，甚至导致通信中断。因此准确预报电离层能反射的最大可用频率（MUF,maximum usable frequency）[1]，在短波通信[2-3]以及电离层探测[4]中具有重要的意义。

电离层的频率预报主要分为2 种，即长期预报[5]和短期预报[6]。长期预报是通过建立电离层参考模型（IRI,international reference ionosphere）[7]，根据太阳活动指数以及电离层月中值参数，预测未来时间电离层的变化情况。正是由于这种月中值特性，长期预报方法在具体时刻的预报存在较大的偏差，往往仅适用于频率的初选[8]。相比于长期预报，短期预报根据电离层短期内会保持相对稳定的电离特性，结合实测数据，通过算法得出短期电离层的变化情况，预报准确性更高，适用性更强。因此，在过去的几十年里，电离层预报的发展趋势也逐步由长期预报向短期预报发展[9]。目前，电离层短期预报方法主要有等效太阳黑子数法[10]、自相关分析法[11]、多元线性回归法[12]、神经网络法[13-14]、卡尔曼滤波（KF,Kalman filter）法[15-16]、相似日法[17]等。其中，等效太阳黑子数法和神经网络法需要大量的历史数据作为输入，而自相关分析法和卡尔曼滤波法需要的历史数据相对较少，因此更常用。文献[18]对比了卡尔曼滤波法和自相关分析法在电离层短期预报的精度，得出卡尔曼滤波法短期预报的性能总体上优于自相关分析法。但对于卡尔曼滤波法，当观测噪声为非高斯干扰噪声或者存在大量观测野值的情况下，滤波精度和稳定性会下降，甚至可能会导致不收敛。本文旨在提出一种强跟踪的稳健卡尔曼滤波（RKF,robust Kalman filter）频率预报方法，改善传统电离层频率预报的准确性。

2 卡尔曼滤波

卡尔曼滤波是1960 年由Kalman 提出的，其基本思想是以分析误差的最小方差为标准，假设系统为线性系统，噪声为高斯白噪声，采用信号与噪声的状态空间模型，根据预测方程和量测方程对系统状态进行评估与预测，是一种最优化自回归数据处理方法。具体地，利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，得到最佳的状态估计值。由于卡尔曼滤波的基本方程在时间域中是递推形式的，递推过程是一个“预测−修正−再预测”的过程，在求解时不需要大量的已知数据，一旦观测到新的数据，就可以根据算法得到新的滤波值，保持结果最优，因此非常便于数据的实时处理和计算机实现，得到广泛的应用[19]。

2.1 传统卡尔曼滤波预测模型

考虑到电离层MUF 的时间离散性，系统的预测过程可看作简单的时间离散、线性随机的动态系统，模型框架如图1 所示，其中，IZ 表示正向推导（滤波），IZ−1表示反向推导的上一时刻的状态。

图1 模型框架

模型表达式为[20]

式(1)是描述随机动态系统状态随时间变化的状态方程，式(2)是描述状态矢量与观测矢量之间关系的量测方程。通过状态方程，可以利用上一时刻（t时刻）的状态随机变量Xt估计出下一时刻（t+1时刻）的状态随机变量Xt+1，估计过程受到随机噪动wt的影响，这种随机噪动也称为动态噪声，其均值为0、方差为Q，服从wt≈N(0,Q)。对于量测方程，状态变量与量测变量之间也受到量测噪声的影响，其均值为0、方差为R，服从vt≈N(0,R)。

式(1)和式(2)所组成的系统模型，可用于预测电离层的最大可用频率，进而得出传统的卡尔曼滤波方法，递推预测过程如下。

协方差矩阵量测更新为

KF 状态和递推转移流程如图2 所示。

图2 KF 状态和递推转移流程

2.2 Huber-M 稳健卡尔曼滤波方法

在传统卡尔曼滤波中，w t和vt为互不相关的高斯白噪声，实现的功能也是最小均方根误差意义下的最优估计。在标准模型里，量测方程中噪声是一种理想的情况，而在实际的量测中，测量值可能会存在野值，一旦量测中含有大量的野值，标准卡尔曼滤波的性能就会大幅退化，甚至是不收敛的。因此本文提出一种基于Huber-M 估计的稳健式卡尔曼滤波方法，来消除量测野值对预报精度的影响。

考虑到实际测量中包含野值的情况，本文改进量测噪声的分布函数，具体描述为

其中，FN为量测噪声的主体分布，保持和原模型一致的高斯分布；FP为污染部分，它可以是方差远大于主体分布的其他厚尾分布；α为污染率，其值越大，代表在实际的测量过程中存在野值的数量就越多。

Huber 最先提出M 估计[21]，其核心是使定义的代价函数取得最小值。本文将该方法应用于传统卡尔曼滤波的观测更新方程中，并对其进行改进。推导过程如下。

首先，定义了t+1 时刻的状态误差为

其中，xt+1为t+1 时刻的状态真实值，为t时刻对t+1 时刻状态的先验预测值。

联合式(2)构造线性回归模型为

定义矩阵

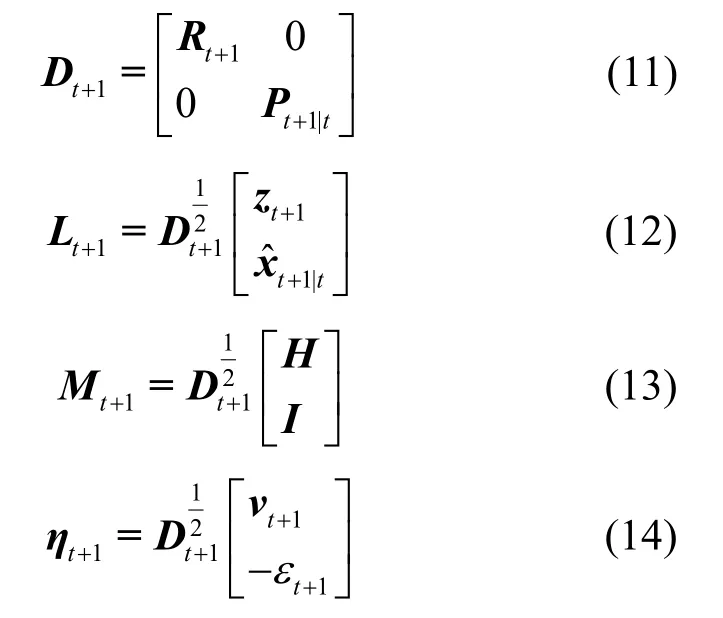
则式(10)可以改写为

定义Huber-M 估计的代价函数为

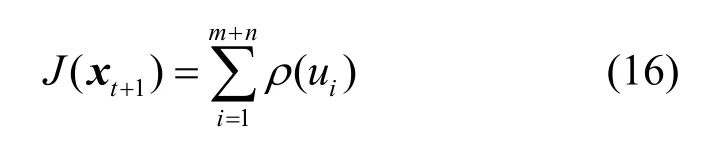
其中，ui为残差向量u=Lt+1−M t+1xt+1的第i个分量；ρ为Huber 函数，表达式为

其中，γ为可调节因子，取值为1～2，本文中，γ=1.345。因为在纯高斯分布的条件下，该值的效率是基于L2范数估计的95%。

当代价函数存在极小值时，本文可以通过对代价函数求偏导的方式对其进行求解。因此对于式(16)，在等式左右两边分别同时对xt+1求偏导，并令其结果等于0。

将上述量测数据值和预测状态值之间的线性回归问题添加到卡尔曼滤波递推公式的量测更新方程中，就得到了Huber-M 估计的稳健卡尔曼滤波，简称RKF。图3 为RKF 状态模型与递推转换的流程框架。

图3 RKF 状态模型与递推转换的流程框架

2.3 递推参数初值确定

由于短波通信频率的日变化性，因此需要对预报前一个月的数据进行日变换统计分析。参考文献[22]中递推参数初值的确定方法，初始化P0、Q、R这3 个参数的初始值。

P0为初始系统状态的噪声协方差矩阵，由于X0是从实测的样本数据获取的，严格为系统真值，因此认为P0=0，即为零矩阵。

对于动态随机噪声和量测随机噪声，如果采用经验进行分析估计，则具有随机性，不便于实际模型的输入。于是本文采用回归系数估计的方法，建立倾斜链路探测站8 月和9 月的回归方程，根据2 个月所得回归方程的系数变化进行估算，确定Q矩阵为

3 数据来源和误差分析方法

分析用到的电离层MUF 样本数据采用重庆、海南、昆明3 个电离层观测站的倾斜探测数据，该数据由中国电波传播研究所计算中心提供。由于短波在单个频率点进行通信时，通信时间具有连续性。结合该特性，本文在选择探测样本数据时，每小时内选取2 个探测频率点作为验证数据，使检验结果更具代表性。

采用均方根误差（ERMS）和相对误差（ΔPD）这2 个指标[23]来评估与分析预报结果的好坏，指标定义分别为

其中，MUFob为某个时刻的探测值，MUFpre为相应时刻的预报值，N为所选样本数据的总数。

4 预报结果比对与分析

图4～图7 分别为2019 年10 月4 日—6 日，重庆到海南、昆明探测站（正向、反向）通过传统卡尔曼滤波（KF）、稳健卡尔曼滤波（RKF）和国际电离层参考模型（IRI）3 种预报方法得到的MUF 预报结果，同时给出不同方法在相同时刻频率预报的误差。

从预报结果来看，IRI 的预报值与实际观测值相比偏差较大，但是在部分时间节点上也能取得不错的预测效果；KF 和RKF 在整个预报过程中都保持着较高的精度和稳定性。

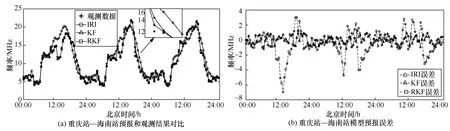
图4 重庆站—海南站的MUF 预报结果

图5 海南站—重庆站的MUF 预报结果

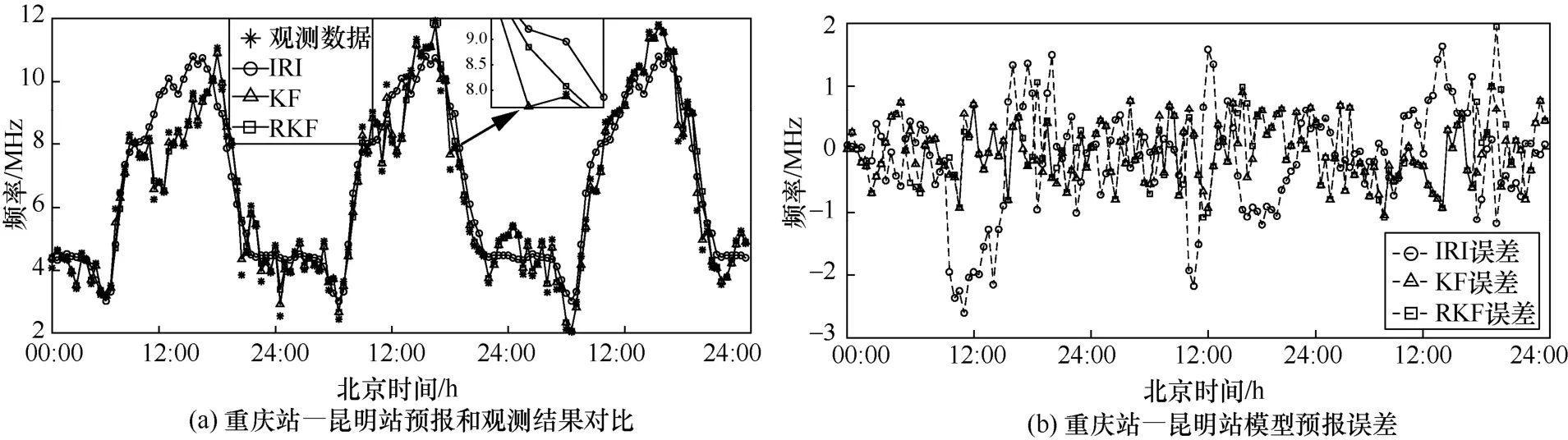
图6 重庆站—昆明站的MUF 预报结果

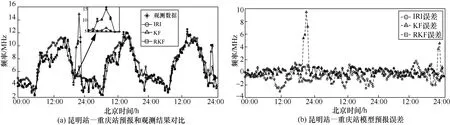
图7 昆明站—重庆站的MUF 预报结果

表1 3 种预报方法的结果分析

表1 分别给出了RKF、KF、IRI 这3 种预报方法在不同探测链路上预报结果的误差分析。在重庆到海南（正、反向）没有观测野值的探测链路上，相比IRI，KF 的平均相对误差降低了6.665%，平均均方根误差减少了1.100 85 MHz；RKF 的平均相对误差降低了6.525%，平均均方根误差减少了1.117 35 MHz。对比均方根误差和相对误差可以得出，RKF 和KF 预报精度均高于IRI。将KF 和RKF两者相比，平均的 ΔRMS=0.0165、ΔPD=0.14%，说明在无探测野值的链路上KF 和RKF 的预报精度相差不大。

在重庆到昆明探测链路上，相比IRI，KF 的相对误差降低了2.48%，均方误差减少了0.383 1 MHz；RKF 的相对误差降低了2.08%，均方根误差减少了0.331 5 MHz，ΔRMS=0.0516、ΔPD=0.4%。但从图7(a)的探测数据看出，实际观测的第一天和第三天在21:00—24:00（夜间）时间段，探测到的最大可用频率异常偏高，根据实测经验夜间短波通信频率较低，该时间段存在探测野值。对于该条链路，若采用KF，均方根误差为1.373 4 MHz，比IRI 高出0.298 7 MHz，滤波性能下降；若采用RKF，则比IRI 的相对误差降低了5.96%，均方根误差也减少了0.468 3 MHz，ΔRMS=0.767、ΔPD=3.59%。结合重庆到昆明的数据分析结果可知，RKF 在有观测野值的情况下性能明显优于KF，稳定性和抗干扰能力更强，具有更好的稳健性。通过图7(b)误差结果分析也可以看出，在存在观测野值的情况下，RKF 的滤波性能最好，KF 次之，IRI 稍差。

最后，根据2019 年10 月多个电离层探测站点探测到的数据，采用本文提出的RKF 短期预报方法，获得MUF 三维曲面，如图8 所示。

选取MUF 频点的85%作为测试频点，在重庆到广州（超过1 000 km）短波通信链路上进行测试分析。通过短波电台，每30 min 呼叫一次，重庆到广州24 h 可通率高于90%；每10 min 呼叫一次，重庆到广州24 h 可通率高于87%。

5 结束语

本文提出的稳健卡尔曼滤波短期预报方法，进一步提高了电离层频率预报方法的准确性。通过对实测MUF 数据变化规律及观测误差产生的成因与特征进行回归分析，利用电离层参考模型作为先验信息，改进卡尔曼滤波模型的状态估计方程；引入代价函数机制，通过Huber-M 估计实现对预报状态的量测更新，消除观测野值带来的污染。验证结果表明，本文提出的稳健卡尔曼滤波方法在实际链路的频率预报上均方根误差和相对误差均优于传统的卡尔曼滤波方法，在昆明到重庆（存在观测野值）的探测链路上，所提方法比KF 的相对误差降低了3.59%，均方根误差也减少了0.767 MHz。能够对电离层的最大可用频率实现更好的追踪，具有更好的稳健性和稳定性。此外，根据多个电离层探测站点探测到的数据，采用本文提出的稳健卡尔曼滤波短期预报方法，获得最高可用频率曲面图，最后通过短波电台，进行了重庆到广州数千米链路的实际通信测试，可通率达87%以上，具有良好的连通率。考虑到短波信道的特点，后续工作将结合不同季节电离层的信道特性、磁暴现象等因素展开进一步的分析与研究。

图8 不同时间、不同距离最高可用频率三维曲面