船舶倾斜对不同行人流疏散效率影响的数值分析

房斯明，刘正江，封室丞，王新建

(大连海事大学，航海学院，辽宁大连116026)

0 引言

客船作为运输旅客的主要交通工具，其安全一直是一个敏感问题，一旦发生事故，后果可能是灾难性的，疏散是降低伤亡的一种有效措施。通过分析船舶疏散过程[1]，发现船舶倾斜会在很大程度上影响船上行人运动，尤其当倾斜程度严重时，行人通常会出现行走困难，进而影响整个疏散过程，使疏散时间增加。例如，2012年载有4229 名乘员的“歌诗达协和号”在意大利海岸附近触礁，触礁事故发生一段时间后，船舶处于右倾状态，且随着倾斜角度不断加大，行人在疏散过程中无法正常行走，需要借助扶手等设施缓慢移动。因此，掌握行人在船舶倾斜状态下的运动特征，将有助于提升紧急情况下疏散过程的安全性和高效性。

针对船舶倾斜状态下的疏散研究起步较晚且研究成果较少，大多局限于行走速度的单独研究。SUN等[2]研制了一个模拟船舶倾斜的走廊装置，通过实验研究了不同倾斜角度对行人快速行走和正常行走速度的影响。KIM等[3]研究了倾斜状态下的人员行为，通过实船仿真，分析疏散过程，预测伤亡人数。KANG 等[4]研究发现，沉船过程中的船舶倾斜角度，行人的移动方向和期望速度在一定程度上影响疏散效率，并在疏散过程中加入了异质行人，发现少量的异质行人会减少疏散时间，对疏散过程起到促进作用。WANG 等[5]通过实船实验，对比船舶在航行过程中遇到小角度倾斜和停泊期间行人正常行走和快速行走的速度，并得出在相同大小的倾斜角度下，所处位置距离横摇中心的距离也会影响其行走速度。德国汉堡水池研究机构(HSVA)结合其他组织的实验研究结果，提出人员行走速度随倾斜角变化的衰减公式，向国际海事组织(IMO)提交了一个有关船舶倾斜疏散的报告[6]，并利用AENEAS 仿真软件模拟了在不同倾斜角度下的人员疏散过程。

船舶进水倾覆过程中，倾斜角会不断增大，对行人紧急疏散提出较大挑战，考虑到实验安全性和经费资助问题，无法再现极端情况下的疏散场景，故使用仿真模型进行研究。本文在基础社会力模型中加入船舶倾斜状态下的行人受力情况，并考虑行人视角问题，对比AENEAS 向IMO 提交报告中的实验数据，验证模型的有效性；并将其应用于多种行人流场景，分析不同倾斜角对人员平均行走速度和疏散时间的影响，确定最佳的疏散策略。

1 改进社会力模型

社会力模型由Helbing[7]首先提出，经不断优化改进，已经被成熟地应用到陆地人员疏散中。基础社会力模型中考虑了行人自驱动力fwill、行人i和行人j间作用力fij和与运动边界(Wall)的作用力fiW。在合力的作用下，质量为mi的行人以加速度移动(vi为行人i在t时刻的速度矢量)，即

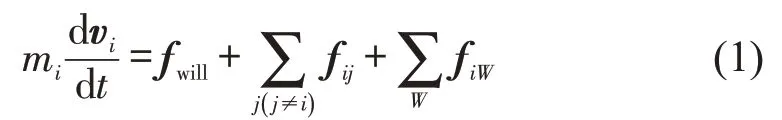
1.1 行人视角

基础社会力模型中，行人会感知其周边所有人，且都对自身产生影响；现实生活中，若周围行人距离目标行人较远，尤其是同向行人，其作用力影响很小。因此，本文在基础模型中增加行人视野问题，即并不是所有行人都会对目标行人产生心理排斥力，定义目标行人的视野区域为其移动方向的[-60°,60°]范围。若两行人间距离超过3 m，目标行人则会在当前时间步中忽略对方的影响。但处在目标行人视野盲区，与其距离较近的行人仍然会产生排斥力，因为在现实生活中会通过声音等方式感知到盲区内距离较近的行人。

如图1所示，实心行人代表目标行人i，其周围分布了10 个人，此时目标行人需要根据自身运动方向，划分视野范围，图1浅色区域代表视野范围，深色区域代表视野盲区。以此确定对其产生作用力的行人，并将他们标记为实线空心行人，而其他不在视野范围内的行人标记为虚线空心。目标行人还需确定视野盲区内距离很近的行人j5，此处暂定视野盲区的行人影响范围为0.6 m，如图1中视野盲区内的浅色区域。最后目标行人根据距离依次计算对其产生影响的行人间作用力。改进后的行人间作用力fij计算公式为

式中：lij为行人间是否产生作用力；dij为行人间的距离；r为行人的视野范围。

1.2 船舶倾斜时行人受力模型

与在平整稳定的陆地建筑物中行走不同，行人在船上行走，尤其当船舶进水倾覆的过程中，会处于复杂的倾斜状态，故本文提出一种在船舶倾斜状态下的行人行走社会力模型(SFMS)，即

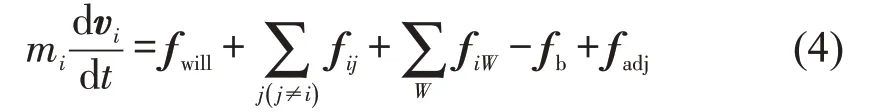
式中：fb为行人受到的倾斜力或由倾斜带来的摩擦力；fadj为行人主观上的自调整力。

如图2(a)所示，行人在船上行走，当船舶发生倾斜时，行人行走方向与倾斜方向相同时，行人相当于行走在一个下坡的走廊，如图2(b)右侧行人。若船舶倾斜角为φ，此时行人受到的倾斜力是沿着倾斜方向自身重力G的分力fb=G×sinφ。如果只考虑倾斜力对行人的影响，行人的速度会不断增加，显然与实际不符。因此，在社会力模型基础上加入一个行人主观上的自调整力fadj。若坡度角较小，该力将有助于行人行走，行人通过有效控制行走姿态，速度也会有微幅上升；当坡度角超过行人可控范围时，行人需要通过自调整力使重心后倾，避免摔倒。行人行走方向与倾斜方向相反时，行人处于上坡情景，如图2(b)左侧行人，在行走过程中，行人受到由倾斜带来的摩擦力fb=G×sinφ。同样，若只考虑摩擦力fb，在社会力合力与摩擦力的抵消作用下，当倾斜角约为15°时，行人即停止运动，但在现实中，行人往往可以克服15°角的坡度。此种情况下，行人一方面受到的摩擦力作用会降低速度；另一方面，通过自调整力调整重心和步态，克服部分摩擦力以更省力的姿态爬坡。船舶倾角正负判断，根据船舶原理中的通用定义[8]，船体处于正浮状态时，平衡水线的位置为WL，如图2(d)所示；若船体向船首倾斜(平衡水线W1L1)，φ为正；若船体向船尾倾斜(平衡水线W2L2)，φ为负。

图1 根据行人视角计算行人间的作用力Fig.1 Force between pedestrians calculated from pedestrian perspective

如图2(c)所示，当行人行走方向与倾斜方向垂直时，相当于行人受到一个侧向力，该力使行人运动轨迹一直朝着较低的倾斜面行走。简而言之，行人在此种情况下，受到的是横倾带来的倾斜力，为方便表达，将该种情景统称为横倾对行人的影响，包含船舶纵倾带给行人在横向行走时的影响和船舶横倾给纵向行走行人带来的影响。实际中，行人遇到此种情况时，往往会通过调整身体状态，寻找可以协助行走的扶手或栏杆，以降低速度为代价，保持身体平衡。因此，在横倾时，行人的自调整力fadj主要用于回正身体状态，克服倾斜力。

结合HSVA 项目报告的研究成果，如图3和图4的AENEAS 曲线，通过MATLAB 线性拟合，发现自调整力随着倾斜角度和行人所受摩擦力改变，得出行人在不同角度的横、纵倾状态下自调整力与倾斜力的规律为

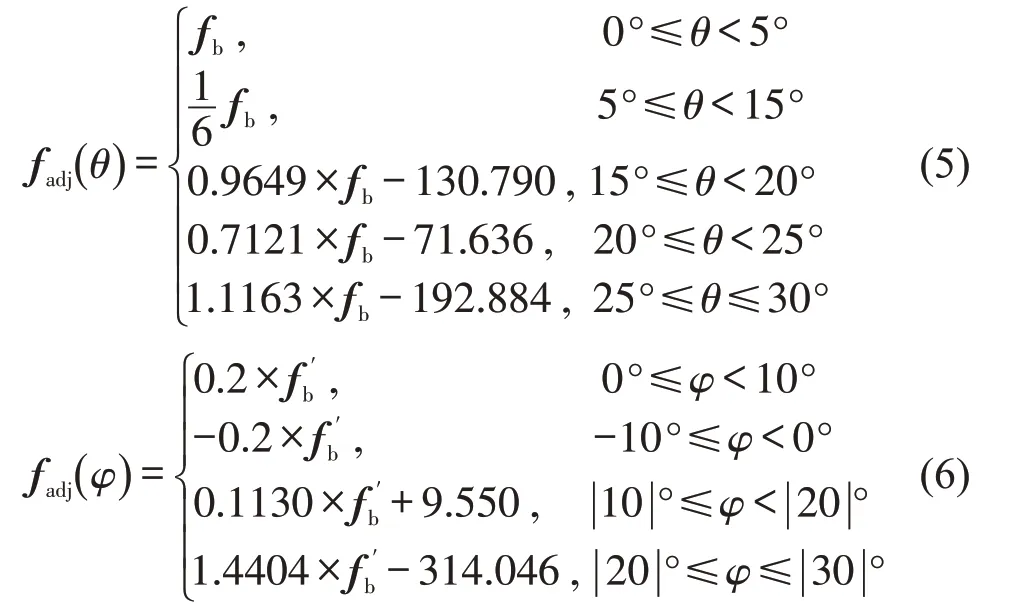
式(5)为横倾状况下的人员自调整力，式(6)为纵倾状况下的人员自调整力。式(6)中fb′为fb的转置矩阵，由于当纵倾角度超过10°后，无论纵倾角的正负，自调整力的计算公式相同，故用 |10|°～|30|°表示。

为避免偶然性，在实验开始前，进行100次横倾角度θ在[0°,30°]，纵倾角度φ在[-30°,30°]的仿真。对比HSVA向IMO提交报告中的速度衰减因子与本文结果发现，本实验与其他实验结果变化趋势一致，验证了实验的有效性，结果如图3和图4所示。

2 仿真结果分析

2.1 仿真场景

实验模拟船上两种走廊行人行走情况，即单向走廊和交叉走廊。单向走廊主要模拟行人仅受纵倾或横倾的单一倾斜作用，交叉楼梯为纵倾和横倾同时作用对行人疏散过程的综合影响，如图5所示。图5(a)、(b)实验场景为一条长20 m，宽2 m 的单向走廊；图5(c)、(d)实验场景为两条相同大小的交叉走廊，夹角为90°。基于上述两种走廊仿真4种场景：场景1 为单向走廊的单向行人流，包含一个20 人的群组，如图5(a)所示；场景2 为单向走廊的双向行人流，包含两个10人的群组相向而行，如图5(b)所示；场景3 模拟交叉走廊中，横、纵向两组行人流，每组行人流由两个10 人的群组组成，如图5(c)所示；场景4 模拟交叉走廊中4 组行人流，每组5 人，如图5(d)所示。图中，箭头表示各组行人的行走方向。行人期望速度和重量分别设置为 1.48 m·s-1，70 kg，且均满足正态分布。

图2 行人在船舶横、纵倾状态下行走示意图Fig.2 Schematic diagram of pedestrians walking under trim and heel condition

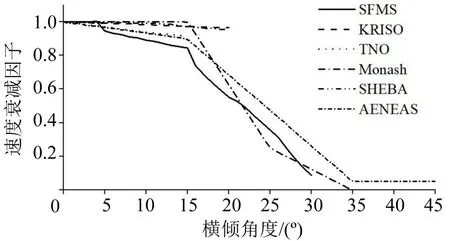
图3 行人速度在不同横倾角度下的衰减情况Fig.3 Attenuation of pedestrian speed at different heel angles

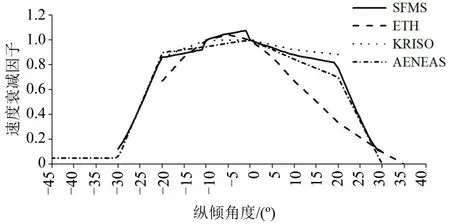
图4 行人速度在不同纵倾角度下的衰减情况Fig.4 Attenuation of pedestrian speed at different trim angles

图5 各种场景的行人流Fig.5 Pedestrian flows in various scenarios

2.2 结果分析

(1)倾斜对疏散速度的影响

根据SFMS模型，通过100次实验模拟，绘制出人员在不同倾斜角度下的平均速度曲线，如图6和图7所示。

实验结果表明，在倾斜状态下，4种场景人员的平均速度走势相近，但也有细微区别。在纵倾情况下，除φ=[-10°,0°]外，场景2人员的平均速度均略大于场景1，差值约为0.082 m·s-1，这是由于场景1中行人流密度较大引起的。场景1 中：当φ为[-10°,0°]时，即纵倾向下状态，行人被视为可控的下坡行走，故其平均速度最大；φ大于0°时，场景1中的行人处于上坡状态，故φ越大，其速度越低；当大角度纵倾(|φ|＞15°)时，各场景中人员疏散速度开始显著下降。相比之下，场景3 和场景4 的平均速度相差不大，场景2 的平均速度约比场景3 和4高出2.25%，说明在大角度纵倾情况下，横向行走的行人受到影响比纵向行走的大。

图6 各场景中纵倾角度对人员平均速度影响Fig.6 Influence of trim angle on average speed of pedestrian in scenarios

图7 各场景中横倾角度对人员平均速度的影响Fig.7 Influence of heeling angle on average speed of pedestrian in scenarios

横倾对疏散速度的影响与纵倾相似，且各场景的速度变化趋势相近，其中，场景1 的平均疏散速度最低，场景4最大。在小角度横倾(θ ＜15°)时，各场景的速度下降较缓；当θ=15°时约减少14.40%，图7中场景2 和场景3 的速度曲线几乎重合；但是当横倾角超过15°时，场景3中的平均速度比场景2大17.38%，这是因为场景3 中有一组行人横向行走，而场景2 中两组行人均是纵向行走，这也说明在大角度横倾情况下，纵向行走的行人受到的影响比横向行走的行人大。

船舶走廊实际宽度可以满足两个正常行人并排行走[9]，因此，可以将场景1中的单向行人流有效分散，即一股同向行人流分为多股同向行人流，从而提高人员疏散效率。对于场景2对向行人流，在疏散交汇过程中应当列队有序撤离，否则行人间的避碰行为会增大疏散时间。在交叉走廊中，重点关注交汇区域的疏散行为，各方向的行人均汇集于交汇区域，极易造成拥堵，即便在小角度倾斜下，行人的疏散速度也会因拥堵而降低。故可在交汇区域安排工作人员进行现场指挥，通过合理安排，尽可能提高各方向的行人通过率，减少交汇区域的拥挤程度。

(2)倾斜对疏散时间的影响

与速度分析不同，疏散时间计算的是从第一个人至最后一个人到达目标点的整体时间间隔，因此在考虑不同倾斜角对整体疏散时间的影响时，以角度变化量Δ(φ,θ)=5°为增量。经过100次仿真，得到各种场景中平均疏散时间随横、纵倾角度变化关系，并运用MATLAB 工具箱拟合关于倾斜角度和时间的变化曲线，如图8和图9所示。

图8 不同纵倾角度的各场景疏散时间和拟合曲线Fig.8 Evacuation time and fitting curve of each scenario under different trim angles

图9 不同横倾角度的各场景疏散时间和拟合曲线Fig.9 Evacuation time and fitting curve of scenarios under different heel angles

纵倾情况下，φ=[-15°,15°]时，各场景的疏散时间变化不大，变化量约为2 s；当 |φ|＞15°时，疏散时间开始显著增加。随着纵倾角度加大，相同增量Δφ内，疏散时间的增加量ΔT也变大，当φ由25°变为30°时，疏散时间达到最大值150 s，时间变化量ΔT也最大，为89 s，增幅为145.9%。与其他场景相比，在大角度纵倾时，场景3的疏散时间明显多于其他场景；但图6速度变化曲线中，场景3的疏散速度并非最低，说明整体疏散时间不仅仅受速度影响，行人流向也对其产生一定影响作用。对不同纵倾角度下4种场景的疏散时间平均值进行数据拟合，得出曲线变化规律，如图8中的拟合曲线。分析可知，在该实验工况下，纵倾角度φ=[-30°,30°]时，疏散时间与纵倾角度呈六次关系。

小角度横倾状态下，疏散时间也没有明显增加，如图9所示；当横倾角度θ ＞15°时，疏散时间开始显著增加，且增加量ΔT大于相同情况的纵倾，此时4种场景的最大平均疏散时间达到163.2 s，相比纵倾最大平均疏散时间131.8 s增加了31.4 s。当倾斜角度大于15°时，同等情况下，横倾相比于纵倾，计算得出的平均疏散时间增加约16.07%。虽然在横倾角度对速度影响的分析中，场景2的平均疏散速度比场景1 大，但是横倾角超过20°时，场景2 的疏散时间最多，与相同倾斜角度的平均疏散时间相比，增加约10.37%。同样，拟合4 种场景在不同倾斜角度下的平均数据得出，该实验工况下，时间与横倾角度仍呈六次关系。

从疏散结果来看，当倾斜角小于15°时，倾斜角度对各场景的疏散速度和疏散时间都没有明显影响，此时为疏散的最佳时机，船舶工作人员应尽快疏散乘客，避免因倾斜角过大使疏散效率降低，进而造成人员拥堵，人员密度增加，进一步阻碍疏散进程。当不得不在大角度倾斜下进行疏散时，相比横倾对疏散过程的影响，纵倾对行人速度衰减的影响较少，故行人应当尽可能调整其运动方向，以便更好地行走。除此之外，行人在走廊疏散时，还可以借助墙边扶手等维持身体状态，调整疏散行为。

3 结论

本文在原始社会力模型基础上增加行人视角问题，以及行人受到的倾斜力和克服倾斜影响的自调整力，利用MATLAB仿真4种不同疏散场景。实验结果发现，速度并不是影响行人疏散的唯一因素，相同船舶倾斜状态下行人不同行走方向也会一定程度地影响疏散过程。相同倾斜角度下，横倾对行人的影响要大于纵倾；小角度倾斜(＜15°)会降低行人平均速度，但没有大幅度增加整体疏散时间；当倾斜角度超过15°时，无论是纵倾还是横倾，疏散时间都会随着倾斜角度的增大而迅速增加。因此，在船舶进水倾覆的紧急疏散过程中，倾斜角小于15°是最佳的疏散时机，应该尽快组织人员进行疏散，使灾害影响降到最低。