基于换道轨迹规划模型的车道级行程时间估计方法研究
管德永,张树鹏,刘海青
(山东科技大学,交通学院,山东青岛266000)
0 引言
随着智能交通与精细化交通信息服务的发展,车道级行程时间研究成为热点。作为车道级行程时间估计的基础,GUO C.Z.等[1]通过使用低成本热传感器与雷达设备,结合全球定位系统(GPS)、惯性导航系统(INS)与视觉测程技术,根据路网拓扑结构及车辆轨迹信息,构建车道级地图。余志等[2]以数据为基础,进行车辆路段轨迹重构。
轨迹规划研究早期在自动机器人领域应用较为普遍,通过搭建轨迹模型,实现机器人的精确移动,如Bezier曲线、K-均值、支持向量回归等[3]模型。KAWABATA 等[4]利用分段Bezier 曲线生成机器人的光滑轨迹,用于实时避障。在车辆换道轨迹规划方面,邓建华等[5]将元胞自动机模型应用于换道决策中,在不同内外因子影响下的换道次数与速度波动规律,对换道机理做出清晰描述。然而,5次多项式模型具有轨迹位置过渡平滑、加速度连续的特点,可以实现有界约束,拥有更大的优势。
传统行程时间估计主要针对长路段路径规划,以路段和交叉口为基本研究单元,较少区分每个车道的交通状态,无法支撑精细化交通信息服务应用,未来车辆的精细化导航需要在车道等微观层面进行剖析。U.CHIDA[6]提出两种出行行为的行程时间估计问题,一种是单调可分链路模型唯一解的优化问题;一种是非单调不可分链路模型考虑OD的非线性互补问题。罗霞等[7]根据浮动车数据建立行程时间融合模型,但无法解决车道级交通状态判别的问题。随着车联网技术的不断发展,行程时间的估计方法逐步完善,IN L.等[8]提出一种压缩感知(CS)方法,提高复杂路况条件下的网联车辆(Connected Vehicles)CVs行程时间估计水平。
为精确高效地估计微观道路下车辆的行程时间,本文采用改进的5次多项式曲线进行车道级路径轨迹的描述,并对进入路段Link 的不同车道、不同车速的换道轨迹进行求解,得到全路段最短行程时间,并通过仿真验证用车道级轨迹进行行程时间估计的合理性。
1 路网模型构建
路网模型构建包括:车辆行驶数据采集与处理、车道级基础路网建模及路网Link划分等环节。
1.1 车辆行驶数据采集与处理
利用车载毫米波雷达、OBD(On Board Diagnostics)采集终端设备获得行驶数据,并提取各路段车辆行驶数据中的有效字段信息:车辆ID、采集时间、经度、纬度,以及转向角。将所得数据进行预处理,清除异常数据和重复数据,统一数据格式,根据时间维度对行驶数据进行排序,形成车辆行驶轨迹时间序列。
1.2 车道级基础路网建模
构建车道级路网模型,为车道级交通状态判别提供微观道路拓扑结构支撑,如图1所示。
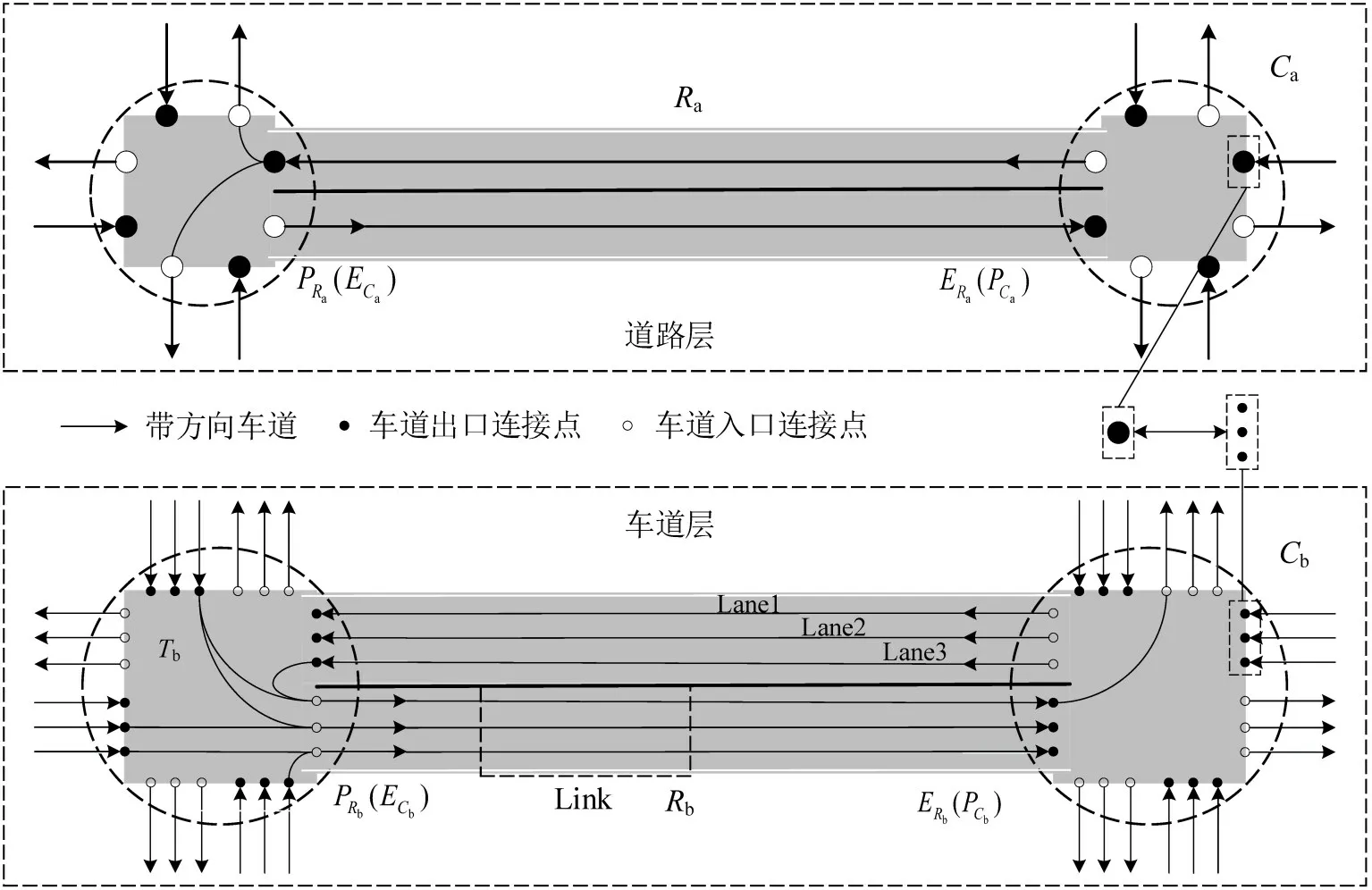
图1 车道级路网模型Fig.1 Lane level network model
道路网络表示为

式中:G为基础路网模型;Ra为道路级的路段集合;Ca为道路级的路口集合;Rb为车道级的路段集合;Cb为车道级的路口集合。
车道级路段集合中的每个路段表示为R(bn),即

式中:n为路段编号;Lanek为第k条车道。
根据道路渠化设计与车辆行驶规则,路网的道路与路口之间可以划分进出的连接点,分别为进入、离开第m个车道级路口的端点集合,分别是为进入、离开第n个路段中各车道的端点集合,i、j分别为路口与车道之间横向和纵向连接点。
车道级路口Cb和路段Rb分别为
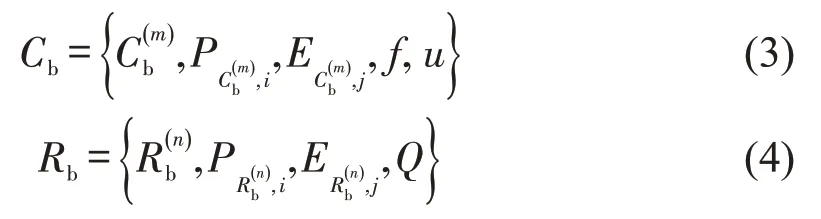
式中:Cb(m)为第m个车道级路口;f为能否通行,1为可以通行,0为不可通行;u为通行方式(直行、左转等);Q为车道属性(车道级别、车道标志线等)。
道路各连接点之间的拓扑关系用交通关联度矩阵Tb表示为

式中:为车道与路口出入端点之间的联系,
1.3 路网Link划分
根据车道级路网模型对路段进行Link划分,如图2所示。将交叉口之间的路段划分为若干个Link单元,单元的节点为Node,根据路段的长度决定单元个数。根据车辆换道情况,分别设置道路Link单元与换道Link单元。
设基础路网中各路段的长度为dn,利用二级长度阈值对各路段进行Link 划分,分别为d1(Link)、d2(Link),且d1(Link)<d2(Link),则路网Link划分表达式为

式中:e、z分别为不同长度阈值下的系数;分别为对应路段剩余长度。
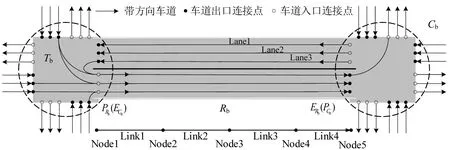
图2 路段Link划分示意Fig.2 Schematic diagram of section Link division
在市区工况下,根据实际道路状况、车辆行驶速度,将道路Link单元设置为200 m。
当dn≤d1(Link)时,以整个路段作为一个Link;当dn >d1(Link)时,由路段下游往上游方向依次进行Link划分,每个Link长度为d1(Link),最后一个Link的长度为路段剩余划分长度d3(Link)。
同理,在城市快速路或高速度行驶情况下,道路Link单元设置为500 m;按照以上划分方法对每一路段中Link 按照由路段下游至上游的顺序依次进行编号。
2 车道级行程时间估计模型
将车辆行驶数据与基于Link 划分的基础路网进行位置匹配,并根据车辆ID对车辆行驶状态进行聚类,使相同ID的车辆信息归为同一集合并分别对多车和单车轨迹数据匹配分析,形成速度热力图,得到单车换道轨迹模型,完成车辆行程时间估计。
2.1 多车轨迹数据匹配分析
道路空间上的Link 单元,可以进行速度标定。根据车辆行驶通过该区域的速度统计,在时间和空间两个维度下将此道路区域的速度表征为

式中:ΔT为研究区域分析时段的时间长度(s);vs,t为路段节点s在t时刻的速度(m·s-1);Mt为在t时刻分析时段的车辆总数量;vi,t为车辆i在t时刻的速度(m·s-1)。速度分布热力如图3所示。

图3 速度分布热力图Fig.3 Thermal diagram of velocity distribution
2.2 车辆换道轨迹规划模型
为精确刻画车辆换道过程的轨迹,采用车辆换道模型,结合路网Link划分基础与道路速度分布热力图进行分析。该模型在多项式生成的基础上,考虑车辆运行状态,确定最小换道时间内的车辆行驶最优轨迹。
通过实际数据检测到车辆在一定时间点上的位置、速度和隶属车道,由实际经验将车辆抽象到隶属车道的中心线位置。Link 内车辆换道模型如图4所示。

图4 Link内车辆换道模型Fig.4 Link vehicle lane change model
图4中,矩形代表车辆;虚线、实线分别代表换道前、后车辆中心线;o、o′分别代表换道的始点、终点,nx、tx分别为曲线的法向量、切向量。则车道中心线r(s)的参数方程为

式中:x(s)、y(s)分别为笛卡尔坐标系中横、纵坐标方程。
对于曲线上二维空间的任意一点(s,d),[s(t0),d(t0)]为换道过程的初始点,坐标表示为
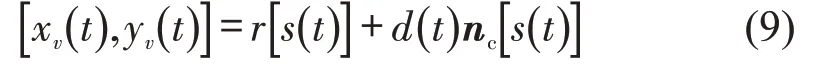
式中:xv(t)、yv(t)为时间变量下的车辆质心坐标位置;s(t)、d(t)分别为换道曲线的横、纵向位移;tc为曲线的单位切向量,即
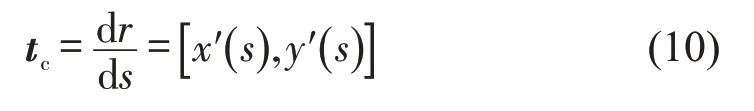
nc为曲线的单位法向量,即
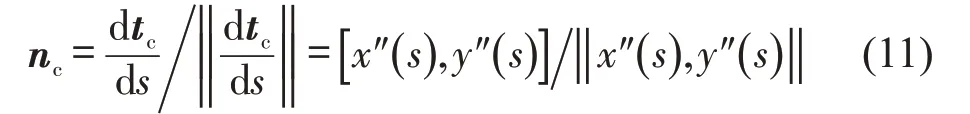
σ为换道曲线的曲率,即

式中:˙为x对变量t求导;x′为x对变量s求导;、y′同理。
根据车辆的初始状态、速度、终止状态,采用5次多项式拟合车辆行驶曲线,设换道时间为tθ,根据不同场景产生约束条件,从而生成最优行驶轨迹。
根据道路交通条件及相关法规,弯道及路口条件不允许超车变道,因此,主要分析车辆直行条件下的换道行为轨迹。直线状态换道如图5所示。
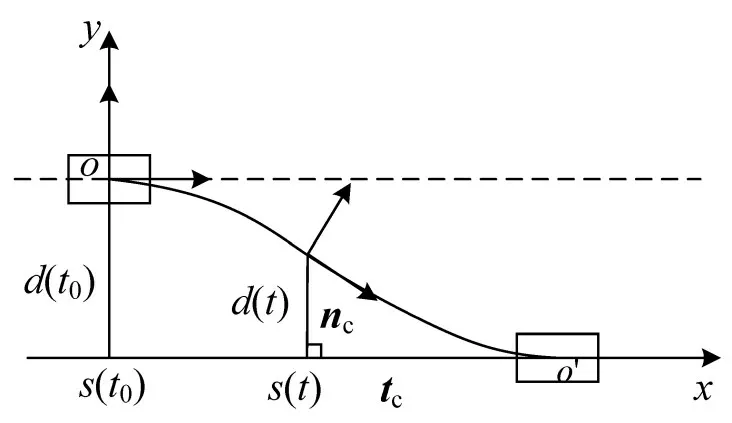
图5 直线状态换道示意Fig.5 Schematic diagram of straight state lane change
直线场景所对应的曲线向量为

该场景下设置5次多项式拟合函数为
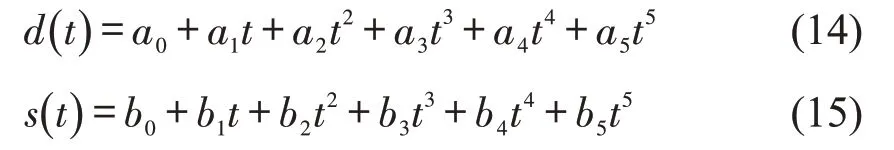
式中:a0~a5、b0~b5分别为5次多项式系数。
根据换道过程车辆状态,可得d(t)为

式中:tθ为车辆换道时间。
根据式(16)和式(17)可得
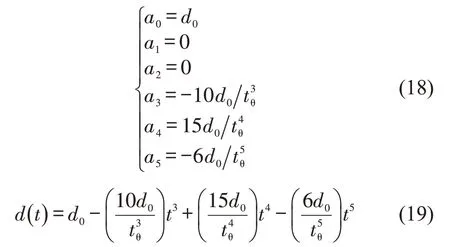
同理,可得s(t)为
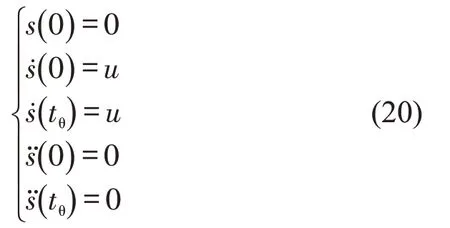
式中:u为车辆换道起始点速度。
根据5次多项式及式(20)可得
和普通输尿管硬镜相比较,输尿管软镜可以到达许多硬镜不能到达的肾盂及肾盏,与PCNL手术相比较又避免了通道建立对肾脏的损伤,因此近年来输尿管软镜越来越多地应用于肾脏及输尿管上段结石的治疗,其适应证也越来越扩大,从结石大小、结石部位都有不同程度的放宽[7,8]。除此之外,术者的经验也越来越影响手术的效果,相同情况下,经验越丰富,手术时间越短,结石清除率越高。但输尿管软镜的使用过程中,仍有一定比例的病例无法上镜,不能顺利进行输尿管软镜下碎石取石,限制了输尿管软镜的更大范围应用[9]。

由式(22)可知,参数方程s(t)与5 次多项式中参数b5有关,令

考虑到车辆行驶过程中的横向加速度为

在一般道路的直线行驶过程中,速度一定,转角小,则横向加速度可以近似为

这里令

整理可得

为使得最大瞬时加速度最小,则
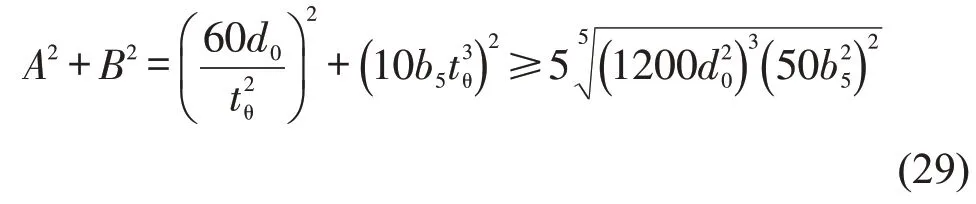
式(29)成立条件为
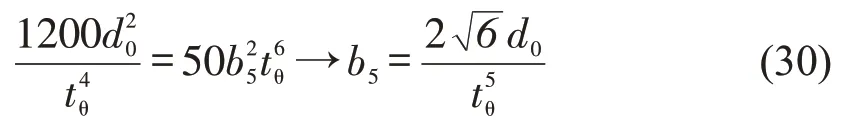
根据实际道路测量状况与速度热力图,车道间距d0和车辆行驶速度u为已知量,车辆换道时间为tθ,因此,参数方程为

根据车辆行驶加速度确定车辆的换道时间,横向加速度较大时,车辆的换道时间较少,由式(31)和式(32)可得
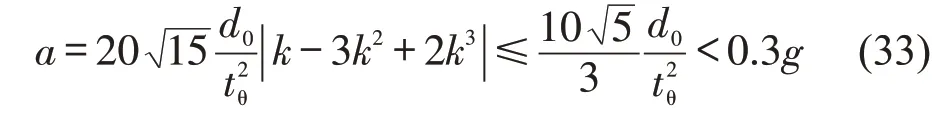
车辆加速度的一般经验阈值为0.3g,g为重力加速度。因此,可得最小换道时间为

车辆换道需要考虑车辆的安全性与舒适性,换道时间不能过长,根据上述参数分析,得到车辆最优轨迹F为
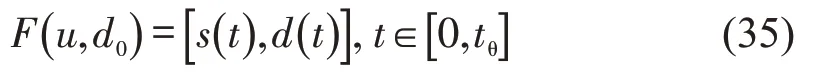
式中:d0为车道之间的距离。
2.3 车道级行程时间估计方法
根据改进的5 次多项式模型,得到路段换道Link 单元内车辆换道的最优轨迹F。以速度热力图为基础,获得换道Link 单元轨迹的换道时间,与道路Link单元的行程时间累加,生成车辆在全路段的行程时间。
当换道Link单元在道路Link单元之内时,有
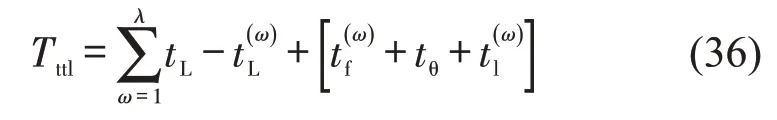
当换道Link 单元在两个道路Link 单元之间时为

式中:Tttl为全路段行程时间;tL为道路Link单元行程时间;ω为换道Link 单元所在的道路Link 单元的编号;λ为道路Link单元的数量;为需要换道的道路Link 单元的行程时间;为需要换道的道路Link 单元下一个单元的行程时间为道路Link 单元中换道之前的行程时间;道路Link单元中换道之后的行程时间。
3 实例分析
选取长度为2215 m 的城市道路作为研究对象,该道路包含2个路段和1个交叉口,属于典型的单向4 车道城市道路,车辆种类较多,各个车道平均速度有较明显的差异,交叉口及路段示意如图6所示。通过PTV VISSIM 软件建立仿真环境,考虑车辆排队,车道选择及交叉口信号的影响,设置车辆轨迹跟踪并记录相关状态数据,包括:车辆ID、仿真时间、车道编号、Link 编号、行驶方向表示、路段编号,以及车辆位置。
在道路路线规划的基础上,对路网进行基础建模,通过交通关联度矩阵Tb,将各车道与路口相连接。规定由南向进口道最右侧为起点,对进口车道顺时针编号,出口车道以同样方式编号。

图6 交叉路段仿真示意Fig.6 Simulation schematic diagram of intersection section

实验选取编号为Vehicle101 测试车辆5 s 的数据,方向为规定的目的地方向,按照Link 划分原则对路网进行划分,在正常市区道路条件下采用标准。时空轨迹数据如表1所示。
由表1可知,车辆起初在该路段第4个Link、第2条车道,后经变道至第3条车道,纵向位置的变化与速度关系服从速度公式。
计算车辆在道路上相同Link、不同轨迹的行程时间。在车辆的变道过程中,由于车道速度不同,导致车辆在不同行驶条件下的轨迹曲线不同,如图7所示。
根据车辆在车道的行驶速度,得到单车轨迹规划,如图8所示。换道轨迹曲线标号1~4,在此Link内,车辆在初始车道以一定的速度直行后进行换道,然后在目标车道继续行驶。
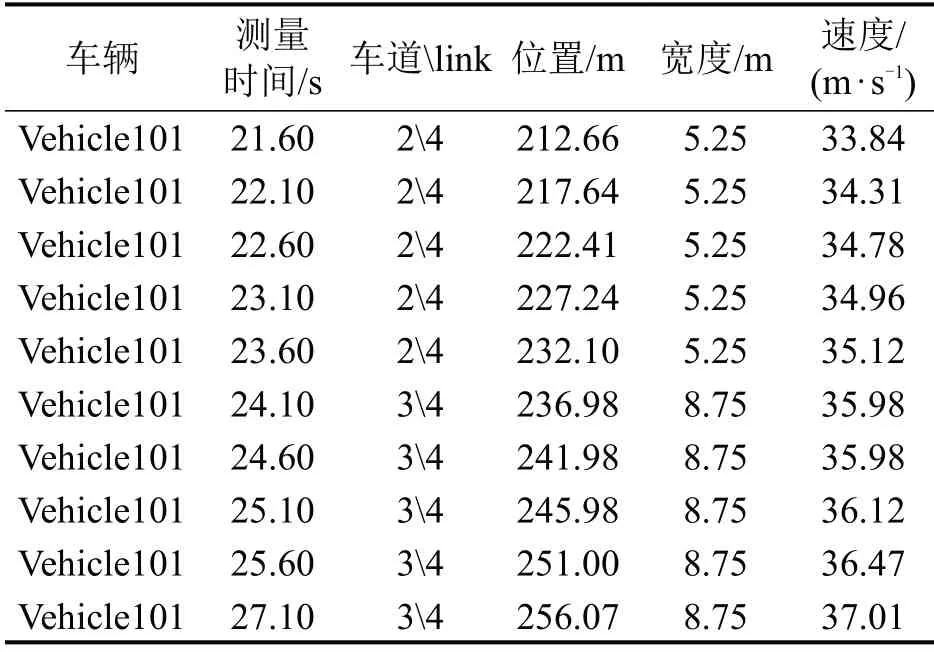
表1 时空轨迹数据示例Table 1 Example of space-time trajectory data
根据单车轨迹规划图,在横向车道距离不变的情况下,纵向位移变化按表2所示的不同车辆换道情况进行分类。
由表2可知,车辆在初始车道中心线换道至目标车道中心线,由于速度变化,换道轨迹改变,纵向位移也因速度的增加而增大,Link内车辆行程时间减少。根据上述图表信息,不同状态下的行程时间最短轨迹如下。
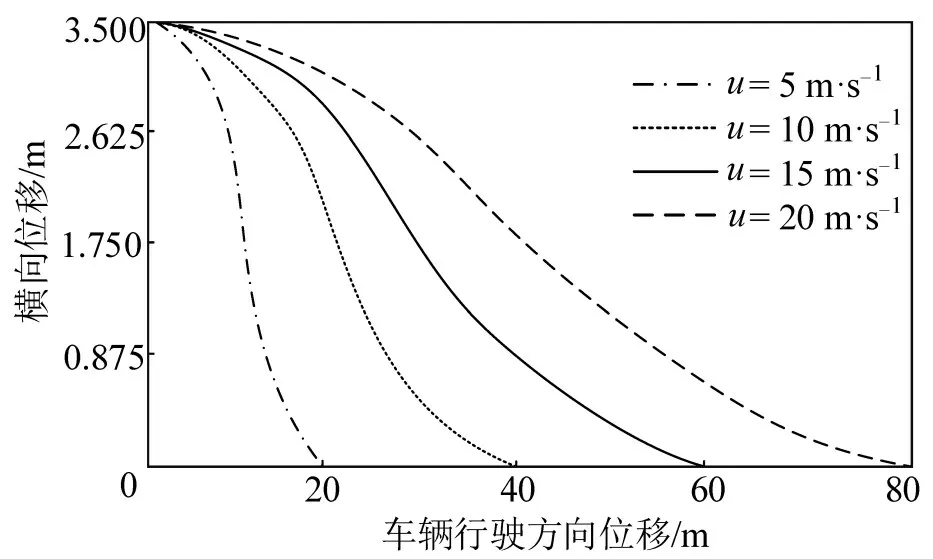
图7 不同纵向速度下的换道轨迹曲线Fig.7 Lane change trajectory curve at different longitudinal velocities
(1)当初始速度和换道后的速度均为15 m·s-1时,有
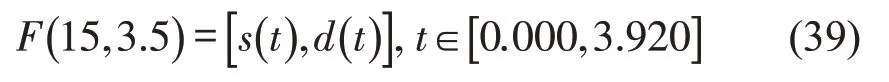
换道轨迹曲线为
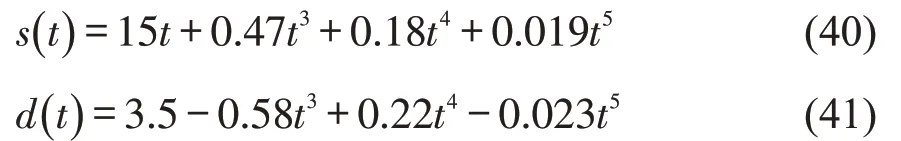
(2)当初始速度为15 m·s-1,换道后的速度均为13 m·s-1时,有

此时,换道轨迹曲线分为两部分,一部分是车辆以15 m·s-1的速度由初始车道中心线位置行驶到车道边界位置,即

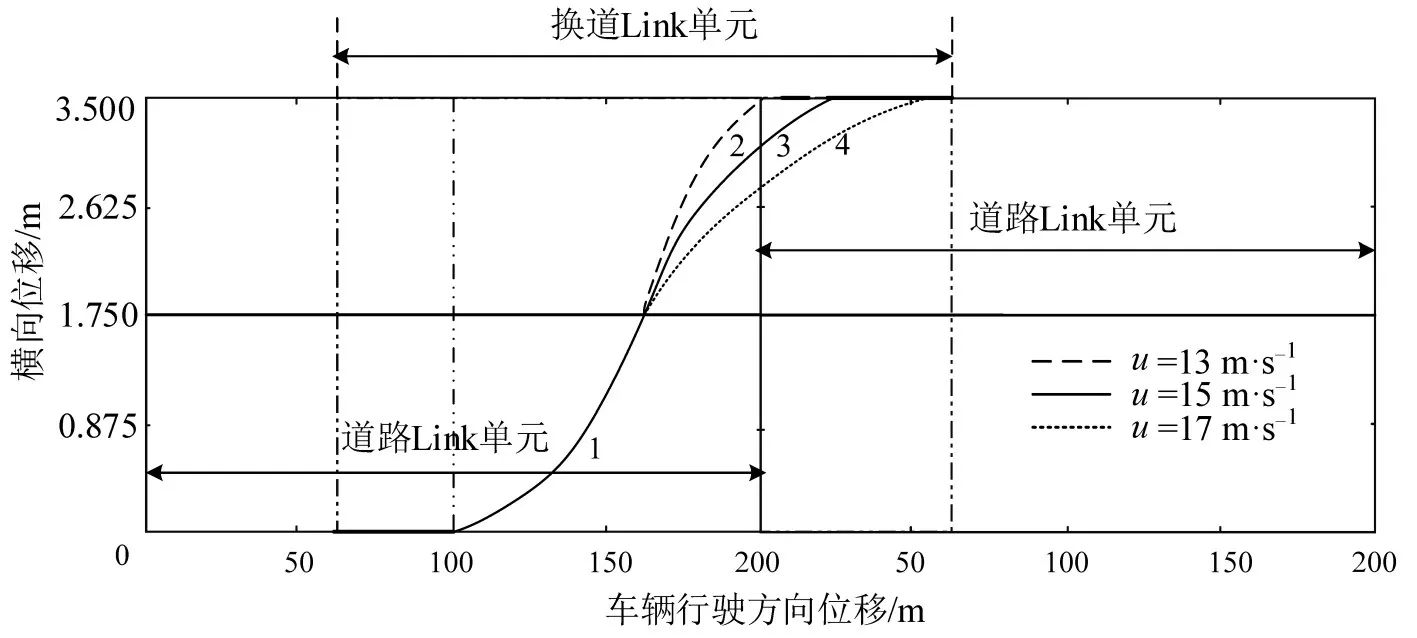
图8 Link单元车辆轨迹规划Fig.8 Link unit vehicle trajectory planning diagram

表2 不同车辆换道情况分类Table 2 Classification of lane change of different vehicles
另一部分是车辆以13 m·s-1的速度由车道边界位置行驶到目标车道中心线位置,即

同理,当初始速度为15 m·s-1,换道后的速度均为17 m·s-1时,换道轨迹曲线可用上述方法表示。路段的行程时间是多个换道Link 单元与道路Link单元行程时间的整合,研究路段的全程行程时间如图9所示。
分析该交叉口及路段全部直行车辆的行程时间得知:全程行程时间众数最小出现在Lane3,换道次数为0次;Lane2最短行程时间与此相接近,且均在第一个Link 换道1 次;车辆平均速度最快的Lane4,在直行方面各项数据并不优于Lane3,均有1,2次变道;平均行程时间、最短行程时间的最小值均出现在Lane3,分别节省25.7%、18.3%的时间,且此车道进入路段的车道较少进行变道。
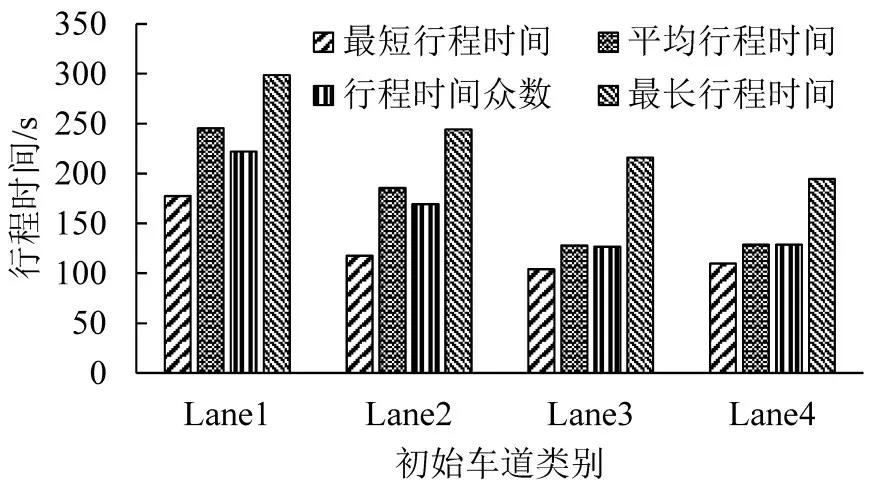
图9 实验路段全程行程时间Fig.9 Simulation section of whole journey time
4 结论
本文将改进的5 次多项式换道轨迹模型引入到车道级行程时间估计问题研究中,不同于传统基于低频GPS数据的估计方法,该模型可以很好地利用轨迹信息,并且生成的轨迹与实际道路行车轨迹吻合度较高;根据实际道路条件设置仿真环境,对换道轨迹进行跟踪仿真,通过Link划分与整合得到车辆在该路段行程时间。结果表明,在路段起、终点之间,该方法能够精准刻画车辆的车道级行驶轨迹,并得到该轨迹下的最短行程时间,完成车道级行程时间估计。

