考虑航艏向与数据变化差异的船舶轨迹预测

高天航，徐力，靳廉洁,2，葛彪

(1.交通运输部规划研究院，水运所，北京100028；2.大连海事大学，交通运输工程学院，辽宁大连116000)

0 引言

随着我国水路运输货物需求不断提升，我国多个港口水域或长江等内河水域已出现船舶流量巨大的情况。船舶流量巨大，船舶密度较高的水域，更容易出现船舶碰撞等事故问题。为此，如何根据船舶AIS数据对船舶实时轨迹进行准确跟踪预测，在船舶交通事故发生前给出有效预警，就显得十分重要。

国内外关于船舶轨迹预测研究采用过：k 阶马尔科夫链[1]，TREAD 方法[2]，Ornstein-Uhlenbeck 随机过程法[3]，粒子滤波器的贝叶斯网络方法[4]，改进的高斯模型[5]等多种不同的方法。而神经网络算法，作为一种非线性、自适应信息处理算法，在与AIS 数据相结合的船舶轨迹预测中更是有所尝试。甄荣[6]、徐婷婷[7]分别利用BP 神经网络算法对航行行为和轨迹进行预测；雷进宇[8]改进传统的二维轨迹预测方式，创新使用三维可视化模型进行更加直观的船舶轨迹预测；徐国庆[9]构建Attenton-LSTM神经网络模型，采用注意力机制突出对船舶航行起关键作用的输入特征，实现对船舶行为的预测；胡玉可[10]构建循环神经网络模型进行船舶轨迹预测，设计基于对称分段路径距离的数据预处理方法，构建基于门控循环单元的循环神经网络模型，实现船舶位置信息精准且高效的预测。综上，已有研究鲜有考虑航艏向数据变化对预测带来误差影响的研究，且鲜有进行针对性的处理。因此，在模型中进行对应改进来解决航艏向数据变化所带来的预测误差问题显得十分必要。

1 基于AIS信息的船舶轨迹分析

船舶AIS 数据包含静态信息和动态信息。静态信息主要涉及船舶的船名、IMO 号、船籍国和船舶载重吨等基本不随时间推移而变化的数据，动态信息包括某一时刻的时间(TIME)、航艏向(COG)、速度(SOG)、经度(LONGITUDE)和纬度(LATITUDE)数据。

对于某一船舶而言，船舶AIS数据动态信息表示其一段时间内的航行行为特征，TIME 表示其时间特性，COG表示其方向特性，SOG表示其速度特性，LONGITUDE和LATITUDE共同表示其空间属性。将一段时间内空间属性所对应的方位点按照TIME 顺序连接起来，就得到该船舶在该时间内的船舶轨迹，即该轨迹由其动态信息中的5种数据共同影响决定。一般假设，船舶下一时刻的船舶AIS数据动态信息与前一时段的船舶AIS数据动态信息存在较强的关系。因此，若要对船舶航行轨迹进行预测就需要将上述5种数据同时纳入考虑。

2 模型构建

2.1 BP神经网络模型

BP 神经网络模型是一种改进的神经网络算法，根据误差反向传播算法进行训练，内部架构如图1所示。

BP神经网络包含输入层、隐含层和输出层3部分。输入层内含n个神经元节点，其编号为i(i=1,2,…,n)，输入向量为u=(x1,x2,…,xn)T，其中，xn代表第n个神经元节点的输入信息；隐含层内含l个神经元节点，其编号为j(j=1,2,…,l)；输出层内含m个神经元节点，其编号为k(k=1,2,…,m)，输出向量为v=(y1,y2,…,ym)T。ωij为输入层神经元与隐含层神经元之间相连接的权重值；ωjk为隐含层神经元与输出层神经元之间的连接权重；θj为隐含层神经元阈值；θk为输出层神经元阈值。

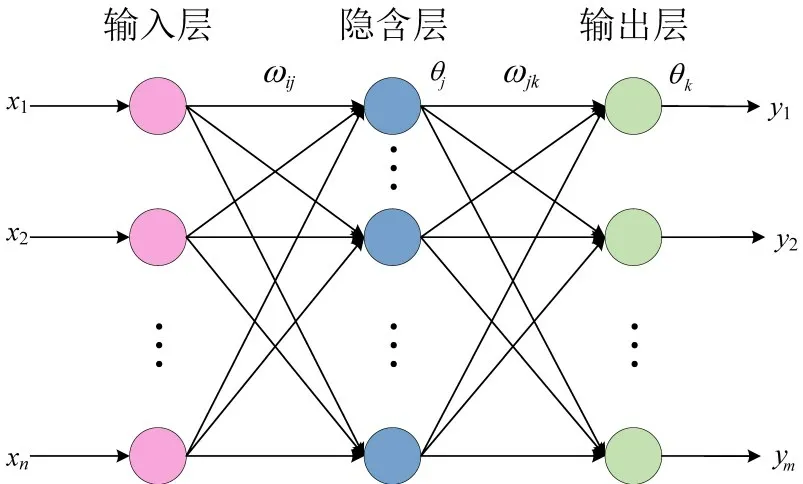
图1 BP神经网络内部架构图Fig.1 Internal structure of BP neural network

BP 神经网络属于有监督学习算法的一种，具体训练步骤如下：

Step 1 初始化参数。根据系统要求准备输入向量u和输出向量v，确定网络输入层和输出层的神经元节点个数，对权重值ωij和ωjk及阈值θj和θk进行初始化设置，选取合适的网络学习速率和传递函数。

Step 2 输入层至隐含层计算。代入ωij和θj，计算隐含层值Hj为

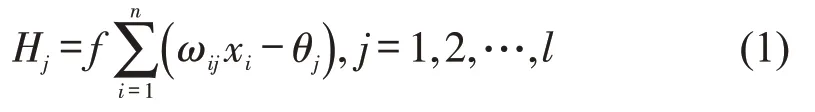
式中：f为从输入层到隐含层的传递函数，常用的传递函数包括双曲正切、Sigmoid函数和Softmax函数等。

Step 3 隐含层至输出层计算。运用已计算得到的Hj，ωjk和θk，通过传递函数计算Ok为

Step 4 误差计算。通过单样本训练方法计算误差，每一个样本，都要根据网络计算结果回传误差进行调整，误差计算方式为

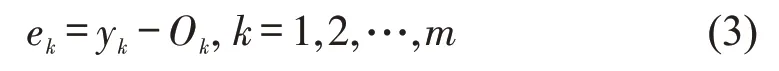
Step 5 权重值更新。根据误差结果ek，采用梯度下降法，计算误差与对应参数的偏导数，得到权重值和阈值的更新值，更新权重值ωij和ωjk，为使误差逐渐得到改善，更新后值为ω′ij和ω′jk。其中，η为学习率，通常在0-1范围内取值。

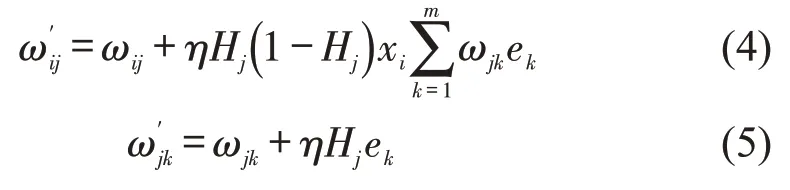
Step 6 阈值更新。根据误差值ek更新阈值θj和θk，更新后的值为θ′j和θ′k，即

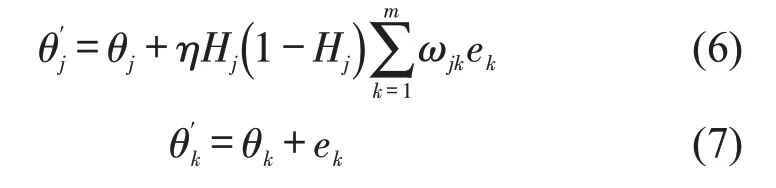
式中：j=1,2,…,l，k=1,2,…,m。

Step 7 计算对比更新后的权重值和阈值的误差，若小于预先设定的误差，则迭代结束；否则，重复Step 2～Step 6，直到满足误差要求为止。

2.2 船舶轨迹预测模型

2.2.1 航艏向变动与数据变化差异处理

在AIS 数据动态信息中，航艏向(COG)代表船舶此刻航行方向，运用0～360间不同数字表示不同方向，以正北为基准按顺时针度量。如图2所示，一般情况下，当船舶航艏向从30变为90，航艏向数据变化为60°。但存在一类特殊情况，当船舶转向恰巧跨越正北向，如从330 变为30，实际船舶转向60°，但在航艏向数据中变化幅度为300°。此种情况，使基于AIS数据动态信息预测该时刻后的船舶轨迹存在比较大的误差。

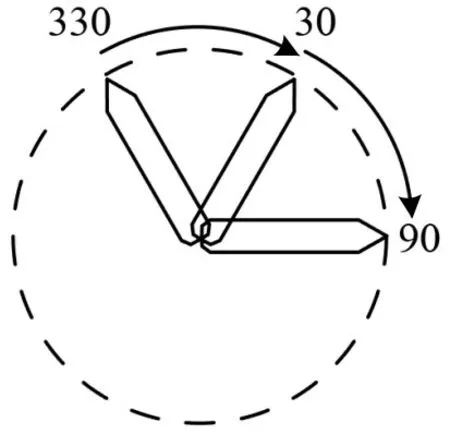
图2 航艏向变化示意图Fig.2 Schematic diagram of heading change

为解决该问题，引入双三角函数，处理航艏向数据，分别计算其正弦和余弦函数值，将其替代航艏向数据引入船舶轨迹预测模型。采用该处理方法的原因是，三角函数可以较准确地体现航艏向度数的周期性变化。考虑正弦和余弦在360°周期内均存在同一函数值对应两种可能度数的问题，同时引入正余弦计算，将航艏向转换值对应角度唯一化。设t时刻的航艏向为Ct，其对应三角函数转换后值为sinCt和cosCt，设为δt和ϕt。

2.2.2 船舶轨迹预测模型构建

基于BP 神经网络的船舶轨迹预测模型是将AIS 历史数据和当前数据作为输入变量，将未来AIS数据动态信息作为输出变量，通过历史数据和当前数据与真实值相对比进行网络训练，建立一种历史和当前船舶AIS 动态信息与未来船舶AIS 动态信息的函数映射关系，预测船舶轨迹。设某一时刻t的经度、纬度、速度和航艏向分别为αt，βt，Vt和Ct，则该时刻船舶的AIS动态信息可以表示为

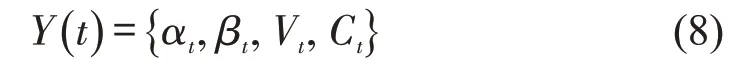
考虑航艏向变动与数据变化差异，将要纳入BP神经网络预测模型的AIS动态信息转换为

选取3个连续时刻t-2，t-1，t的AIS数据转换信息Z(t-2)，Z(t-1)和Z(t)作为输入变量，将t+1 时刻的动态转换信息Z(t+1)作为输出变量，训练模型参数，函数关系为φ，Z(t)i表示包含的第i种信息。得到船舶轨迹预测模型函数为

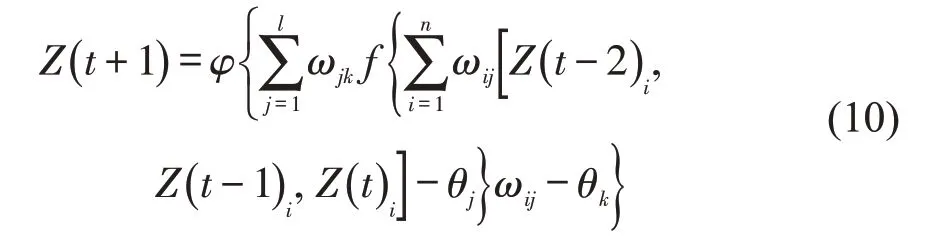
虽然完成了对船舶轨迹的预测，但仍需将Z(t+1)重新转换为Y(t+1)，进行反三角函数转换，反正弦与反余弦在360°内均对应两个数值，将两者相对照便可得到唯一航艏向。

4个反三角函数变化后的数值为

经过BP 神经网络训练或预测后的δt和ϕt与原始数据有可能存在微小偏差，故选取反正弦值C′(t+1)，C″(t+1)与反余弦值中数值相近的两个值进行平均处理，降低误差的基础上实现逆转换，得到训练或预测中的航艏向C(t+1)。

需特别注意，该模型是基于分析历史AIS数据动态信息进行预测，为保障预测精度，需保证所获取历史数据时间间隔较短，相邻AIS数据动态信息间存在着较强的关联性和相似性。

3 实例分析

AIS数据动态信息中的经纬度、速度和航艏向在实际中的数值范围不相同，经度范围为-180°～180°，纬度为-90°～90°，速度一般在0～20 kn，航艏向处于0～360之间。将不同数量级差距代入函数会存在预测误差较大的情况，为解决该情况，采用离差标准化方法，将所有数据均转化为[0,1]数据，即

式中：x为AIS 数据动态信息的原始数据；X为原始数据所构成的集合；minX为原始数据中的最小值；maxX为原始数据中的最大值。由此，既消除了因数据量纲差异所带来的误差影响，同时保留了数据的相对关系，得到转换后的训练数据x′。

通过宝船网(https://www.myships.com)选取某一实际船舶作为研究对象，截取其2020年6月23日某时间段的260 组船舶AIS 数据动态信息，时间间隔3 min，筛除问题数据后作为样本数据。其中，80%作为训练数据，20%作为验证数据，共拥有15个输入神经元节点，5个输出神经元节点。

使用Matlab R2017a 计算，得到AIS 数据动态信息的拟合结果。为验证本文方法在模型拟合与船舶轨迹预测方面的精确度提升，同时进行不考虑航艏向变动与数据变化差异的神经网络模型船舶轨迹预测，结果如图3所示。

图3 运算误差对比图Fig.3 Comparisons of operation error

由图3可知：改进方法在经度、纬度、航速和航艏向4 个方面的均方差分别为0.00086，0.21194，0.05102 和4.65336，原始方法的均方差为0.20908，0.62978，0.55823 和779.24740；考虑航艏向变动与数据变化差异的改进模型比不考虑该情况的传统神经网络模型误差幅度大幅降低，即改进方法误差更小且更加稳定。具体分析发现，当船舶航速出现波动变化时，即时高时低，对原始方法影响较大，其出现经纬度、航速和航艏向误差较大情况。

本文提出模式是一种采用历史数据对未来轨迹预测的模型，船舶后续轨迹与预测轨迹的误差作为评判模型预测是否准确的依据。为此，在该拟合结果基础上，对选取260 组船舶AIS 数据动态信息之后的3组数据进行预测，误差结果如表1所示。

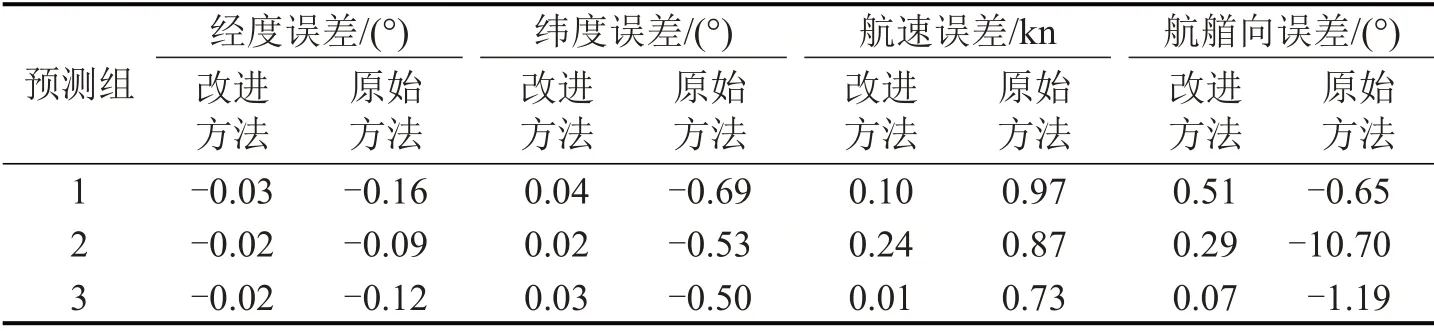
表1 预测误差对比Table 1 Prediction error comparison

由表1可知，本文改进模型误差更小，经度、纬度、航速和航艏向的最大误差分别-0.03°、0.04°、0.24 kn 和0.51°，传统方法的最大误差为-0.16°、-0.69°、0.97 kn 和-10.7°。

4 结论

本文基于BP 神经网络模型，创新性的引入双三角函数变换，将其正弦与余弦两个值作为基础数据纳入BP 神经网络模型，降低航艏向和数据表示在零度方向附近变化带来的差异。经过实例验证，由于改进方法平滑处理了航艏向数据变化在零度方向附近的跨越性，误差均方差大幅低于传统BP神经网络模型。因此，本文所提出的引入双三角函数的方法，是一种BP 神经网络模型针对具体问题的深化，具有一定的理论意义。同时，由于其实例验证有效降低了预测误差，提高预测精确性，证明其在实际应用中更具有实用意义。