基于时空特性和组合深度学习的交通流参数估计
张文松,姚荣涵
(大连理工大学,交通运输学院,辽宁大连116024)
0 引言
城市经济和人口的快速增长使机动车保有量和居民出行需求不断增加,导致城市道路拥堵问题日益严峻。为预防交通拥堵和事故发生,智能交通系统(Intelligent Transportation System, ITS)能获取并准确估计实时的交通流参数。交通流参数估计是ITS提供实时信息的重要前提,越来越受到学者的关注,很多方法被应用于交通流参数估计,包括:自回归积分滑动平均(Autoregressive Integrated Moving Average,ARIMA)模型[1]、K 近邻(K-Nearest Neighbor,KNN)算法[2]、支持向量机(Support Vector Regression, SVR)[3]等。随着计算机技术的迅猛发展,更多的机器学习方法逐渐涌现,给交通流参数估计带来了新的思路。在众多机器学习方法中,深度学习能从海量数据中深入挖掘和捕捉序列规律,故深度学习也被应用于交通流参数估计,具体方法包括:卷积神经网络(Convolutional Neural Network, CNN)[4]、长短期记忆(Long Short-Term Memory, LSTM)神经网络[5]、门控循环(Gated Recurrent Units,GRU)神经网络[6]、卷积长短期记忆(Convolutional LSTM,ConvLSTM)神经网络[7]等。
研究表明,单一估计方法较难完全捕捉交通流参数的规律[8],有学者为提高估计精度,使用组合方法进行交通流参数估计[8-11]。ZHANG Y.R.等[8]将交通流分为趋势、确定和波动3 部分,使用光谱分析法、ARIMA 模型和Glosten Jagannathan Runkle-广义自回归条件异方差模型分别预测交通流的这3部分。基于SVR模型和CNN,罗文慧等[9]提出一种交通流参数组合预测方法。还有学者采用小波分析和LSTM 神经网络提出交通流参数预测的组合方法[10]。为更好地捕捉交通流的时空特性,MA D.F.等[11]使用CNN捕捉交通流数据的空间规律,利用LSTM神经网络捕捉交通流数据的时间规律,基于这两种深度学习方法对交通流参数提出一种组合预测模型。
现有估计交通流参数的研究,大多没有充分考虑交通流的时空特性,忽略了上下游断面之间交通流的密切关系;另外,交通流数据多以时间序列的形式存在,只有足够深入挖掘时间序列的特征才能获得理想的估计效果。目前,大多方法仅使用一种方法挖掘交通流数据在时间上的规律,一些组合方法在交通流数据挖掘的深度和广度方面还不够深入。因此,本文将上游断面的交通流数据作为估计目标断面交通流参数的辅助数据,采用CNN 捕捉交通流序列在空间上的规律,引入LSTM 和GRU神经网络同时挖掘交通流序列在时间上的规律,通过方法融合提出一种基于深度学习的交通流参数估计方法。
1 深度学习-交通流参数估计模型
定义目标断面p的交通流数据序列为,其中,为第t个时间间隔目标断面p的交通流数据,T为分析期内的时间间隔数。基于序列及其上游断面交通流数据构造估计模型所需的输入矩阵,其中,xt,p为第t个时间间隔目标断面p的输入向量,h˜为使用所选模型进行一次估计时所选目标断面p的历史数据个数。
1.1 CNN
构造输入矩阵后即可使用CNN进行交通流参数估计。CNN 包括:输入层、卷积和池化层、全连接层和输出层。将输入矩阵放入输入层,通过卷积和池化层提取输入矩阵的特征,卷积和池化层的输出[4]为
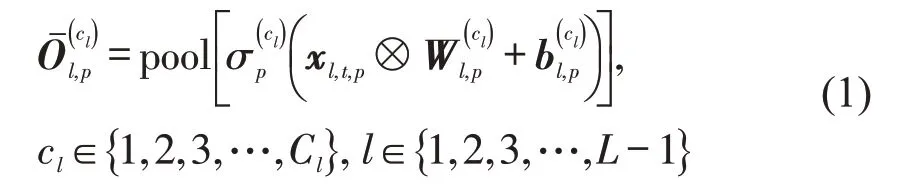
然后,将卷积和池化层的输出放入全连接层,此前对其进行扁平化操作,即
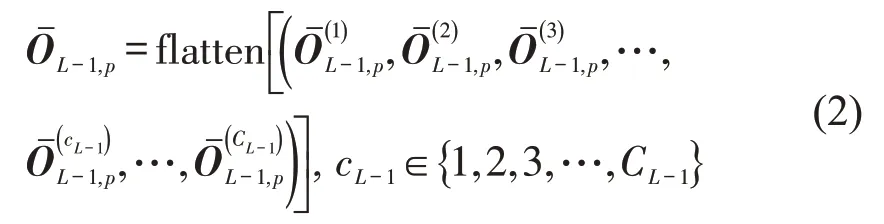
式中:为对第L-1 层输出进行扁平化操作后所得目标断面p的输出;flatten 为扁平化操作;为第L-1 层使用第cL-1个卷积核进行卷积和池化后所得目标断面p的输出;CL-1为第L-1 层卷积核个数。
最后,经全连接层可得交通流参数估计值,即
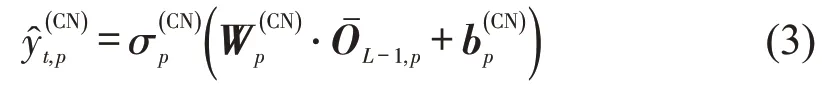
式中:为CNN所得第t个时间间隔目标断面p的交通流参数估计值;σp(CN)、Wp(CN)和bp(CN)分别为CNN 全连接层对目标断面p所选激活函数、权重和偏置向量。
由于风筒出口至工作面距离不同流场分布状况也不尽相同,取风筒中心平面z=2.4 m的速度等值线进行分析,如图2所示。
1.2 LSTM神经网络
LSTM神经网络由输入层、隐藏层和输出层组成,其中,隐藏层包括输入门、遗忘门和输出门。输入矩阵X′p对应隐藏层的记忆信息为,其中,ht,p为LSTM神经网络所得第t个时间间隔目标断面p的记忆信息,第t个时间间隔输入门、遗忘门和输出门的输出分别为it,p、ft,p和ot,p[5],即

式中:ht-1,p为LSTM神经网络中第(t-1)个时间间隔目标断面p的记忆信息;σp(I)、σp(F)和σp(O)分别为输入门、遗忘门和输出门对目标断面p所选激活函数;Wp(I)、Wp(F)和Wp(O)分别为输入门、遗忘门和输出门对目标断面p所选权重;bp(I)、bp(F)和bp(O)分别为输入门、遗忘门和输出门对目标断面p所选偏置向量。
第t个时间间隔目标断面p隐藏层单元的状态ct,p可表达为
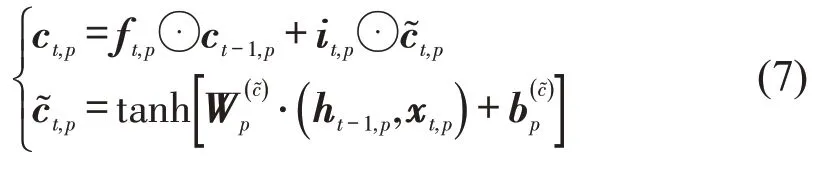
式中:ct-1,p为第(t-1)个时间间隔目标断面p隐藏层单元的状态;⊙为哈达玛积;为计算ct,p时产生的变量;tanh 为双曲正切函数;、分别为计算时所选权重、偏置向量。
基于ot,p和ct,p可得ht,p,即

将隐藏层的记忆信息放入全连接层得到LSTM神经网络在第t个时间间隔内目标断面p的交通流参数估计值,即

式中:σp(LS)、Wp(LS)和bp(LS)分别为LSTM 神经网络全连接层对目标断面p所选激活函数、权重和偏置向量。
1.3 GRU神经网络
GRU 神经网络由输入层、隐藏层和输出层组成,隐藏层包括更新门和重置门。输入矩阵Xp′对应的隐藏层的记忆信息为,其中,为GRU神经网络所得第t个时间间隔目标断面p的记忆信息。相应地,GRU神经网络中第t个时间间隔目标断面p的更新门和重置门的输出分别为zt,p和rt,p[6],即
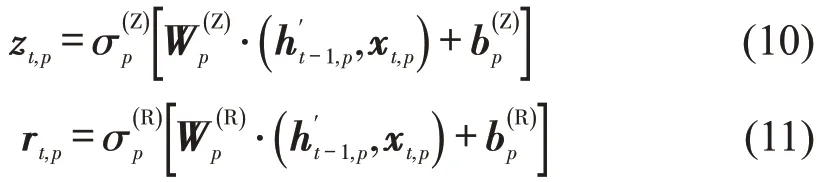
式中:h′t-1,p为GRU 神经网络所得第(t-1)个时间间隔目标断面p的记忆信息;σp(Z)、σp(R)分别为更新门、重置门对目标断面p所选激活函数;分别为更新门、重置门对目标断面p所选权重;分别为更新门、重置门对目标断面p所选偏置向量。
基于zt,p和rt,p计算h′t,p,即

式中:为计算h′t,p时产生的变量;、分别为计算时所选权重、偏置向量。
将隐藏层的记忆信息放入全连接层得到GRU神经网络在第t个时间间隔内目标断面p的交通流参数估计值,即
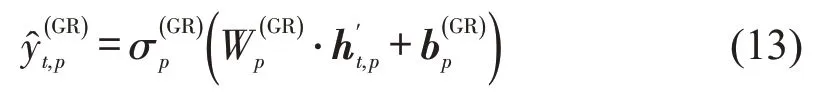
式中:σp(GR)、Wp(GR)和bp(GR)分别为GRU 神经网络全连接层对目标断面p所选激活函数、权重和偏置向量。
1.4 深度CN-LS-GR模型
使用CNN 挖掘交通流在空间上的相关性,引入LSTM和GRU神经网络共同捕捉交通流在时间上的规律,将这种组合模型称为CN-LS-GR 模型。将、ht,p和h′t,p放入全连接层得到CN-LS-GR模型在第t个时间间隔内目标断面p的交通流参数估计值,即
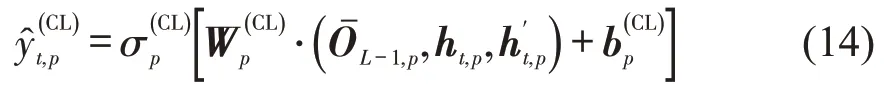
式中:σp(CL)、Wp(CL)和bp(CL)分别为CN-LS-GR 模型全连接层对目标断面p所选激活函数、权重和偏置向量。
CN-LS-GR模型包括3条路径,实施步骤如下:
Step 1 根据交通流的时空特性,使用目标断面和上游断面的交通流数据序列和构造CNLS-GR模型所需的输入矩阵,并将其进行归一化后放入输入层。
Step 2 使用2 层Conv 层和1 层Pooling 层捕捉交通流数据的空间规律,使用2层LSTM层和GRU层捕捉交通流数据的时间规律。
Step 3 将卷积和池化层的输出、LSTM神经网络和GRU神经网络隐藏层的记忆信息进行拼接后放入全连接层,利用交通流历史数据对CN-LS-GR模型进行训练。
Step 4 判断模型是否满足精度要求或达到最大迭代次数,若是,则输出交通流参数估计值;否则,返回step 3继续训练。
CN-LS-GR模型结构如图1所示。

图1 CN-LS-GR模型结构Fig.1 Structure of CN-LS-GR model
2 实例分析
使用中国安徽省合肥市和美国加州萨克拉门托的实测交通流数据验证CN-LS-GR 模型的准确性和可靠性。选取KNN 模型及CNN、LSTM、GRU、ConvLSTM 神经网络和CNNs-LSTM 模型[11]作为对比模型。
2.1 性能指标
使用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error,RMSE)评价CN-LS-GR模型及对比模型的性能。MAPE、MAE和RMSE计算式为


根据图1所示CN-LS-GR 模型,经过测试,第1条路径中第一、第二Conv 层的神经元数分别为16和32,第2 条路径中第一、第二LSTM 层的神经元数分别为16 和32,第3 条路径中第一、第二GRU层的神经元数分别为16 和32,Dropout 层的丢失率均为0.15,激活函数均为Relu 函数。选择MAE作为损失函数,采用Adam 算法对CN-LS-GR 模型进行训练,目标为最小化MAE,训练迭代次数取100,批大小取64。KNN 模型历史数据个数取7;综合模型深度和性能,CNN、LSTM、GRU 和ConvLSTM 神经网络的隐藏层数取3,第一、第二、第三层隐藏层单元数分别取16、64、32;CNNs-LSTM 模型包括2 层Conv 层、1 层Pooling 层和2 层LSTM 层,2 层Conv 层的单元数依次为16 和64,2层LSTM 层的单元数依次为16 和32,其他参数与CN-LS-GR模型相同。
2.2 案例1验证结果
从OpenITS 网站“http://www.openits.cn/”下载中国安徽省合肥市蜀山区内的交通流数据集,选取利用微波检测器获取交通量的4 个断面为研究对象,所选交叉口和断面位置如图2所示,其中断面4在断面1上游,断面9在断面6上游,该区域潮汐交通特征明显。获取2016年7月11日-15日、7月18日-22日及8月8日-12日共15 个工作日的检测器数据,将包含小客车和载货车的交通流数据作为研究数据,采样时间间隔为15 min。图3为断面1 和断面4的交通流变化情况。
由图3可知:在不同工作日,各断面的交通量波动规律大体相同;断面1 和断面4 均有早、晚高峰,上下游断面的交通量变化规律具有一定相似性。因此,在估计下游断面交通量时,将上游断面的历史数据作为辅助数据,挖掘上游断面与目标断面交通流数据的空间关联性,提高交通流参数估计精度。以估计断面1和断面6在8月8日-12日的交通量为例,验证CN-LS-GR模型的性能,其中,使用7月11日-15日和7月18日-22日的交通流数据构造输入矩阵。
以PC(CPU: Intel(R)Core(TM)i7-7700HQ @2.80 GHz, GPU: NVIDIA GeForce GTX 1050Ti)为实验平台,在Python 的TensorFlow 2.0 中搭建CNLS-GR模型。估计断面1的交通量时,基于序列X˜1和构造所需输入矩阵;估计断面6的交通量时,基于序列和构造所需输入矩阵,其中目标断面和上游断面的历史数据个数均取6。图4为8月8日-12日交通量的各模型估计值和实测值。

图2 所选交叉口和断面位置示意图Fig.2 Locations of selected intersections and sections

图3 交通量变化Fig.3 Variations of traffic volume
由图4可知:各模型所得估计值均与实测值的整体走势相同,各估计曲线均与观测曲线较接近,说明各模型的参数设置是合理的;相比其他模型,KNN 模型估计值在峰值处偏离实测值,可见KNN模型性能略差。
表1为断面1 和断面6 中7 种模型的平均性能指标,表中加粗的数字为最小值。由表1可知:相比KNN模型,其他6种深度学习模型的性能指标普遍更小,表明深度学习方法优于传统机器学习方法;相比现有模型,CN-LS-GR模型3个指标均最小,断面1 处MAPE 降低7.51%~26.59%,断面6 处MAPE降低5.72%~21.07%,说明CN-LS-GR模型最优。
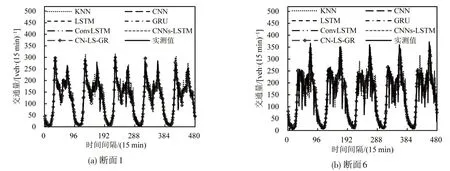
图4 交通量实测值和估计值Fig.4 Observed and estimated values of traffic volume

表1 各模型在断面1和断面6的性能指标Table 1 Performance indices obtained from each method for Sections 1 and 6
2.3 案例2验证结果
从PeMS网站“http://pems.dot.ca.gov”下载美国加州萨克拉门托US-50走廊中的交通流数据集,获得311974线圈检测器和311903线圈检测器于2020年7月20日-9月20日共9周的交通量数据,采样间隔为5 min。数据预处理后,剔除2020年7月20日、8月1日、8月9日-16日、8月24日-31日、9月1日和9月17日的交通量数据,得到43 d 的交通量数据,包括31 d 工作日和12 d 周末。图5为311974 检测器和311903 检测器所处位置,311903 检测器位于311974检测器上游。将这2个检测器在7月20日-9月13日筛选后所得交通量数据作为历史数据,估计311974 检测器在9月14日-20日的交通量。
图6为工作日和周末各模型的平均性能指标,图中MAPE 单位为%,MAE 和RMSE 单位为veh·(5 min)-1。由图6可知:对于工作日,各深度学习模型与KNN模型的MAPE相近,但前者的MAE和RMSE 远小于后者的MAE 和RMSE;对于周末,各深度学习模型的3 个指标均远小于KNN 模型的3个指标;无论工作日还是周末,CN-LS-GR模型的3个指标都比较小。
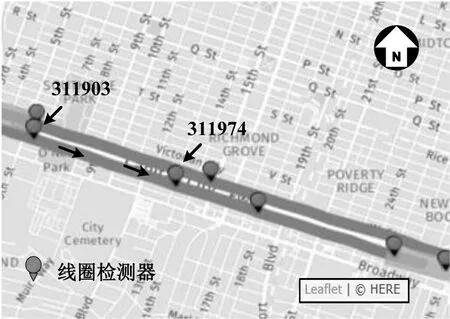
图5 所选线圈检测器位置示意图Fig.5 Locations of selected loop detectors
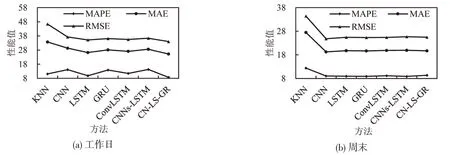
图6 各模型在工作日和周末的性能指标Fig.6 Performance indices obtained from each method on weekdays and weekends
表2为各模型在2020年9月14日-20日一 周的平均性能指标。由表2可知,CN-LS-GR 模型各指标均最小,其中,MAPE 降低6.40%~28.58%,进一步表明CN-LS-GR模型最优。

表2 各模型在311974检测器的性能指标Table 2 Performance indices obtained from each method for Sensor 311974
2.4 案例3验证结果
为验证所提模型在特殊场景下的性能,对案例2 获取311974 线圈检测器和311903 线圈检测器于2019年6月10日-7月7日和12月2日-29日的交通量数据,其中,7月4日和12月25日分别为美国独立日和圣诞节,这2个重要节日的交通量明显小于正常工作日的交通量。将这2 个检测器在6月10日-7月3日和12月2日-24日筛选后所得交通量数据作为历史数据,分别估计311974 检测器在独立日和圣诞节的交通量。
图7为各模型在独立日和圣诞节的性能指标,图中MAPE 单位为%,MAE 和RMSE 单位为veh·(5 min)-1。由图7可知,各深度学习模型的3个指标均远小于KNN模型的3个指标。
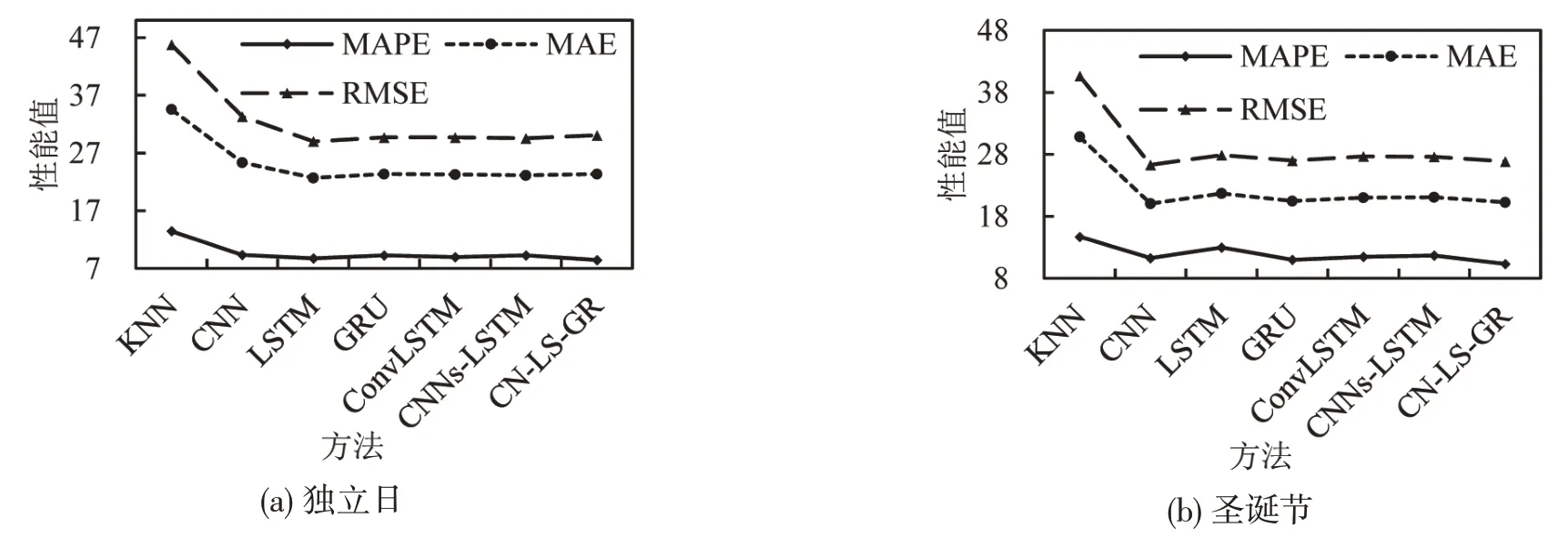
图7 各模型在独立日和圣诞节的性能指标Fig.7 Performance indices obtained from each method on Independence Day and Christmas Day
表3为各模型在独立日和圣诞节的平均性能指标。结果表明,相比现有模型,CN-LS-GR 模型的MAPE 降低7.02%~33.29%,其MAE 虽最小但与其他深度学习模型的MAE 接近,说明CN-LS-GR模型的性能在重要节日也是最优。

表3 各模型在重要节日的性能指标Table 3 Performance indices obtained from each method on holidays
3 结论
针对道路交通流,提出一种基于深度学习的组合估计方法。首先,利用目标断面及其上游断面的交通流数据构造输入矩阵;然后,使用CNN捕捉输入数据在空间上的规律,使用LSTM 和GRU 神经网络同时挖掘输入数据在时间上的规律;最后,将这3种模型的输出放入全连接层,获得交通流参数估计值。将6 种现有方法作为对比模型,选取MAPE、MAE 和RMSE 这3 个性能指标,使用微波和线圈检测器数据验证CN-LS-GR 模型的性能。研究结果表明:CN-LS-GR模型的性能优于所选各种现有模型的性能,在工作日、周末和节假日亦有最优的性能表现,说明该模型具有很高的准确性和稳定性。因此,为提供更准确可靠的交通流信息,建议使用CN-LS-GR模型进行交通流参数估计。

