基于康奈尔笔记法的Nyquist判据教学方法研究
王立国, 刘 丽
(哈尔滨工业大学电气工程及自动化学院,化工与化学学院,哈尔滨150001)
0 引 言
自动控制原理课程中的Nyquist 稳定判据是美国Harry Nyquist于1932 年提出的用于确定动态系统稳定性的一种图形方法[1-3]。Nyquist稳定判据的贡献突出在两方面[4-8]:①从时域到频域,解决了微分方程模型的复杂求解问题;②应用开环传递函数分析闭环系统的稳定性,降低了求解的维数。但由于Nyquist稳定判据需要根据s平面上奈氏图与(-1,j0)点的包围关系来进行定量分析,会对初学者造成如下困惑[9-10]:①在(-∞,+∞)内奈氏图与实轴多次相交时难以把握环绕次数;②当奈氏图从无穷远处开始时,起点与终点间如何构成封闭曲线难以判断。教学中经常发现Nyquist稳定判据的应用误判,亟待探究一种易于理解的Nyquist判据教学方法。
康奈尔笔记法由康奈尔大学的Walter Pauk 博士提出[9],以Keywords(关键词)、Notes(注解)及Summary(概括)为主要特征,涵盖Record(记录)、Reduce(简化)、Recite(背诵)、Reflect(补充)、Review(复习)5 个阶段,故又称为5R笔记术,目前该方法已在化学、生物、医学、计算机教学与深度阅读、英语阅读及大学英语听力理解中得到成功应用[11-15]。鉴于Nyquist稳定判据机理分析的抽象性、分析对象的多样性,应用康奈尔笔记法建立其思路复杂的学习与求解方案尤其必要。
本文以哈尔滨工业大学-伊顿联合实验室为依托,针对Nyquist稳定判据教学及实践教学中存在的问题,从教学理念、教学内容、教学方法等实践环节方面进行改进。依据康奈尔笔记法将Nyquist 稳定判据适用的稳定性分析进行5R 归纳,总结为开环传递函数极点分析、幅频特性与相频特性分析、典型环节频率特性、逆时针环绕(-1,j0)点次数分析、正负穿越分析、开环Nyquist曲线不能构成闭合轨迹分析等特定学习要点,注解其作用与实质。所做工作有助于学生对Nyquist稳定判据内容的深入理解,教学思路构建与具体案例相结合,促进自动控制原理这一课程教学与国际知名院校的接轨。
1 康奈尔笔记法
康奈尔笔记法是根据艾宾浩斯遗忘曲线[16]展开的,是以5R为特征的集记录、复习、自测和思考于一体的笔记方法。通过笔记本三栏区间划分,将课前预习、自测与复习相结合,快速、准确地进行课堂记录,方便快速查找重点、有条理地学习、提炼内容要点、有针对性地思考;康奈尔笔记法的核心在于记录、简化、背诵、补充与复习。以Nyquist 稳定判据学习为背景,相应的康奈尔笔记总结如下。
1.1 Record(记录)
Record(记录),在最大的笔记栏(Notes)中先进行快速直接的记录与收集,突出记录对象的本质特征、数学机理与应用条件。
(1)Nyquist稳定判据的基本概念。如图1 所示,Nyquist稳定判据:立足于Cauchy定理之上,设P 为系统在右半s平面开环极点数、Z为系统在右半s平面闭环极点数;当ω 从-∞变化到+∞时,系统的开环频率特性G(jω)H(jω)按逆时针方向包围(-1,j0)点次数为N,定义Z =P-N,则闭环控制系统稳定的充分必要条件是Z =0。
(2)Nyquist稳定判据的前期知识点复习。如图2所示,Cauchy定理:设Ω 是复平面的一个单连通的开子集,f:Ω→ 是一个Ω 上的全纯函数;设γ 是Ω 内的一个分段可求长的简单闭曲线;无论γ是自交还是卷绕数多于1,只要γ能够通过连续形变收缩为Ω 内的一点,则满足:

图1 Nyquist稳定判据的基本知识点总结

与G(jω)H(jω)相对应,设F( s )为s 平面内的函数、L 为s 平面内逆时针旋转的封闭曲线且不经过F( s )的零极点;P1为F( s )位于封闭曲线L 内的极点数、Z1为F( s )位于封闭曲线L 内的零点数;N1为F( s )按逆时针方向包围(0,j0)点次数,则F( s )稳定的充分必要条件是Z1=P1-N1=0。
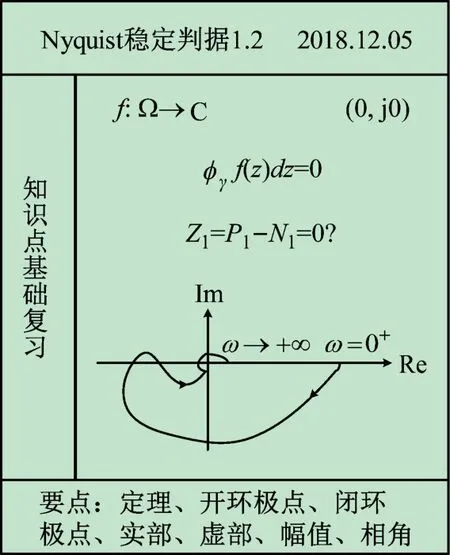
图2 Nyquist稳定判据学习的前期知识概括
1.2 Reduce(简化)
Reduce(简化),提炼重点,专注于从纷繁冗杂的知识信息中获取关键词、关键语句,提纲契领,以便跟上授课速度,提高课堂学习效率。Nyquist 曲线绘制规则:
(1)时域到频域的计算基础

(2)频域传递函数的环节简化。如图3 所示,式(2)~(5)可分为如下特征环节:
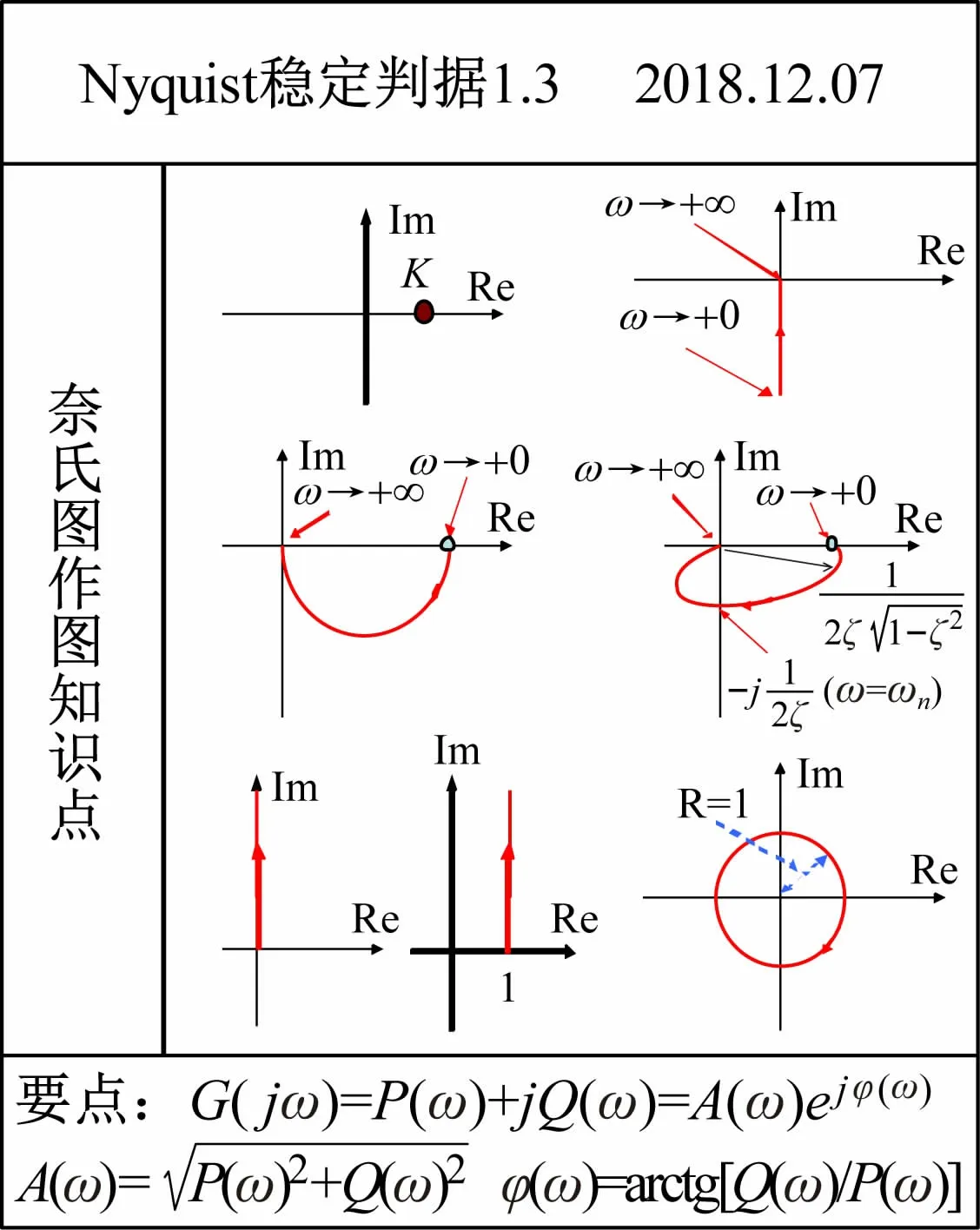
图3 传递函数的特征环节奈氏图
比例环节
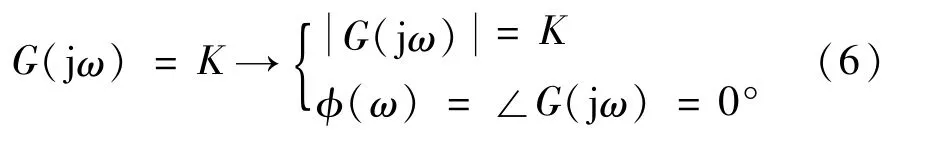
积分环节
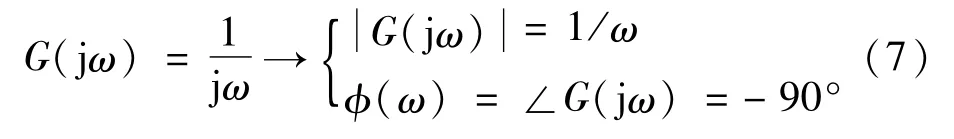
惯性环节
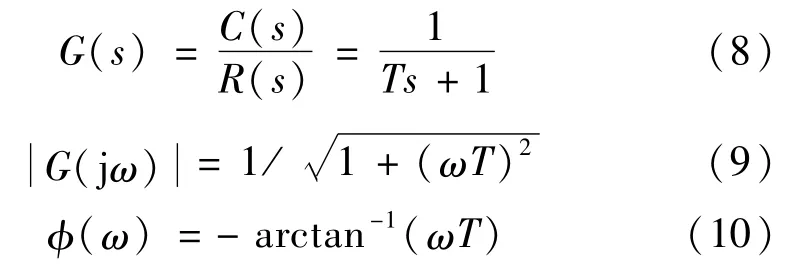
振荡环节
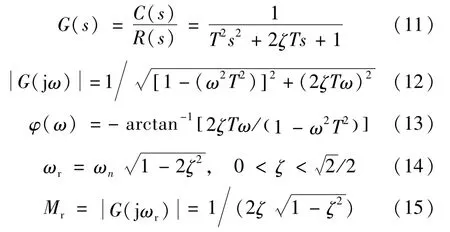
微分环节
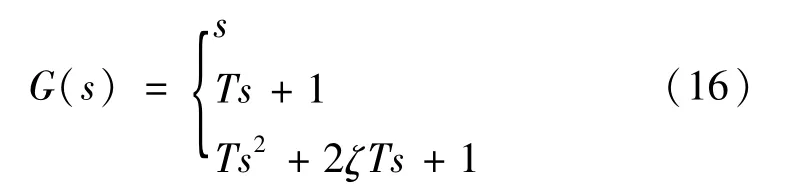
滞后环节
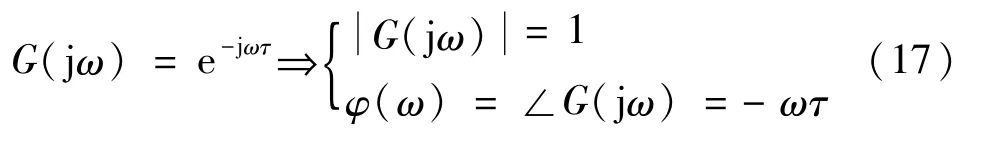
1.3 Recite(背诵)
Recite(背诵),通过重点与资料的对照,转化出可以执行的学习行动。核心思想在于突出内容的实质与深度,力求精简,方便记忆。根据讲义,Nyquist稳定判据的应用准则总结为如下两种情况:
(1)奈氏图与负实轴(-∞,0 )只有一个交点。① 起点G(0+)H(0+)和终 点G(+∞)H(+∞);②与实轴对称补足( -∞,0-)部分奈氏图;③确定P,应用Z =P - N 进行稳定性判定,其中N 为在( -∞,+∞)区间内G(jω)H(jω)按逆时针方向包围( -1,j0)点次数; ④ 如图4 所示, 以为终点、( -1,j0)为起点构建矢量,然后以(-1,j0)为圆心、令所构建矢量沿着奈氏图(逆时针/顺时针)旋转,判断从到转过的角度α,若α =n·( 2π),n =1,2,…,则N =2n;若矢量逆时针绕(-1,j0)旋转,则N为正、反之为负。

图4 Nyquist稳定判据应用1
(2)奈氏图与负实轴(-∞,0 )有多个交点。①确定起点G(0+)H(0+)和终点G(+∞)H(+∞);②正穿越:当ω∈ (0,+ ∞),开环幅相曲线(Nyquist 曲线)从s上半平面穿过负实轴的(-∞,-1 )段到s 下半平面,穿越次数定义为N+;反之称为负穿越,穿越次数定义为N-;③ 要点:ω∈ (0,+ ∞),穿过负实轴的(-∞,- 1 )段;( -1,0 )段穿越无效;④ 与Z =P -N 相对应,此时Nyquist 稳定判据定义为Z =P -2 (N+-N-),详见图5。
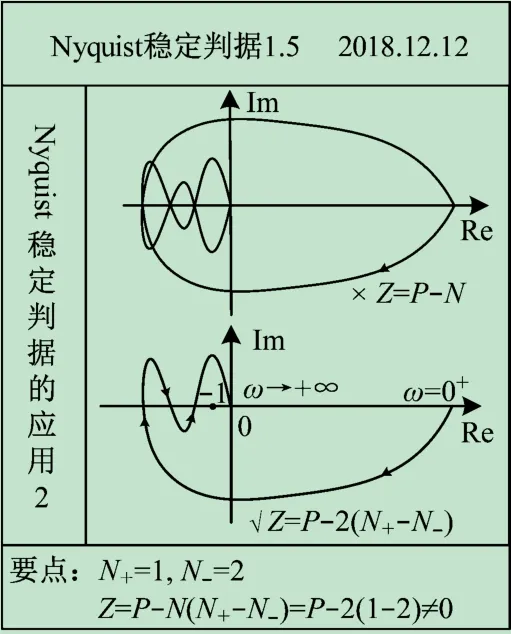
图5 Nyquist稳定判据应用2
1.4 Reflect(补充)
Reflect(补充),对Nyquist稳定判据常规有了了解后,对于开环传递函数中包含积分环节的奈氏图需要单独处理,因为此时奈氏图起始于无穷远处,不构成封闭的曲线(不满足Cauchy 定理),此时需要补足积分环节造成的缺陷。
当控制系统开环传递函数为如下形式时:

由于系统中含有v 个积分环节,奈氏图起始于无穷远处,开环Nyquist 曲线不能构成闭合轨迹,无法确定Nyquist曲线包围(-1,j0)点的圈数N。
如图6 所示,需要先把开环幅相曲线补为封闭曲线,方法是从原开环幅相曲线的ω =0+这一点,逆时针补画半径为无穷大的v ×90°圆弧,并用虚线表示;即一个积分环节补90°,v个积分环节补v×90°。
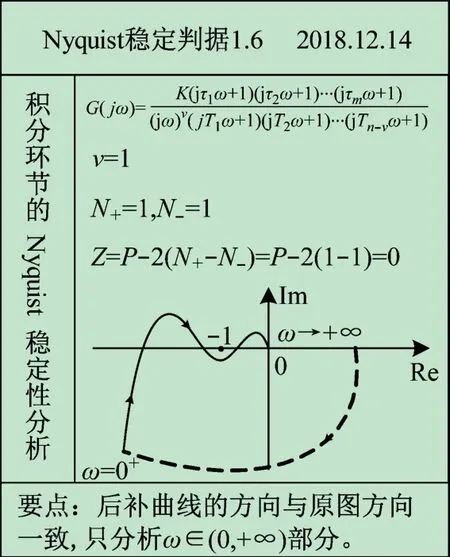
图6 含积分环节奈氏图Nyquist稳定性分析
教学过程中,体现的难点在于,补足v ×90°后,学生不清楚后补曲线的方向性,此时最简捷的方向判定方法就是令后补曲线的方向与原奈氏图方向一致,而且只分析ω∈(0,+∞ )这一部分奈氏图。
1.5 Review(复习)
Review(复习),Nyquist稳定判据在笔记中主要突出频域分析、奈氏图绘制、不同情况下的Nyquist 判据表现形式等,核心在于总结关键词,提炼应用准则、浓缩要点。与式(18)相对应(n个极点、m个零点)。
1.5.1 频率特性
涵盖幅频特性与相频特性,其中实频特性与虚频特性分别表示如下:
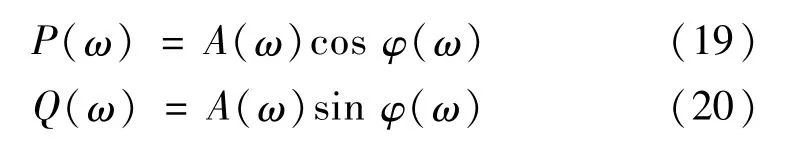
1.5.2 绘制奈奎斯特图
如图7 所示,核心问题:① ω→0+时,低频段从何处出发?②ω→+∞时,高频段以何种姿态收敛?③在ω为何值时穿越实轴和虚轴?④ 与坐标轴的交点为多少?给出每一点处的幅值与相角。
(1)ω→0+时,低频段的表达式为:

ω→0+时,满足表1 所示计算数据。
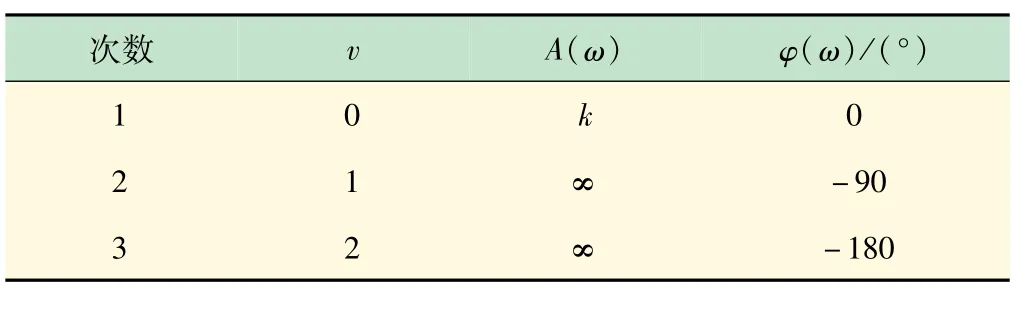
表1 不同数量积分环节的出发点幅值与相角分析
(2)ω→+∞时,高频段幅频和相频特性为:
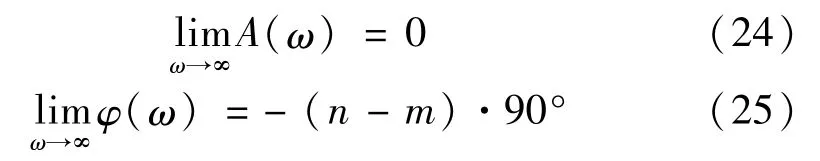
满足如下规律:①n -m =1,曲线沿负虚轴向原点收敛;②n - m =2,曲线沿负实轴向原点收敛;③n-m =3,曲线沿正虚轴向原点收敛。
图7 所示是对Nyquist稳定判据的图形总结,可解决学生对起始于无穷远处奈氏图画图、补足全图及稳定性分析的困惑,简单直观、易于理解。

图7 Nyquist稳定判据准则总结
2 实例分析
已知某单位负反馈系统开环传递函数为:
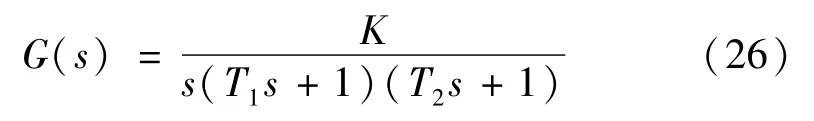
试用奈奎斯特判据判断闭环系统稳定性。
应用康奈尔笔记法求解过程如图8 ~11 所示。
图8 所示为时域到频域、起点到终点的计算过程;图9 所示为奈氏图与实轴交点的计算过程;图10 ~11分别展示了如何将起始于无穷远处的奈氏图补足及应用Z =P -N及Z =P -2 (N+-N-)进行稳定性分析的具体过程。与图1 ~7 相对应,借助于康奈尔笔记法,此实例可将Nyquist 稳定判据应用过程系统、直观地展示给学生。

图8 Nyquist频率特性分析

图9 奈氏图相关绘制过程
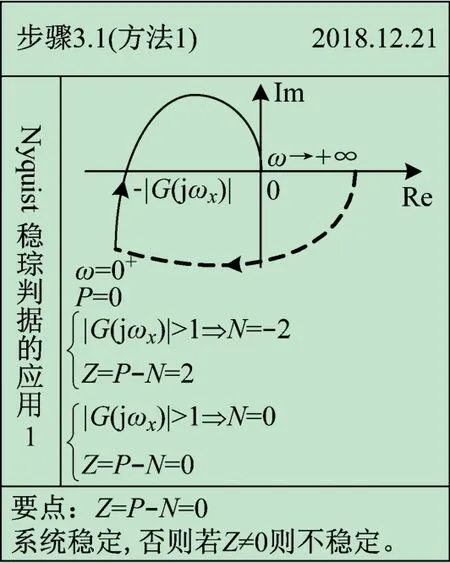
图10 应用Z =P-N方法的Nyquist稳定性分析
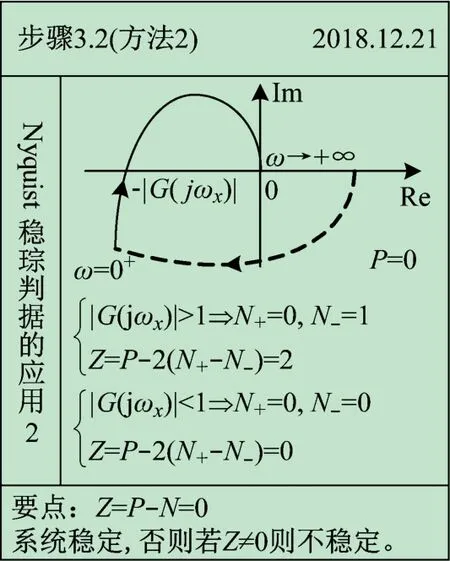
图11 应用正负穿越方法的Nyquist稳定性分析
3 结 语
基于康奈尔大学笔记法思想,将其与自动控制原理教学中的Nyquist 稳定判据有机结合,建立机理分析、绘制规则、稳定判据与康奈尔大学笔记之间的逻辑教学体系,突出记录、简化、背诵、补充与复习5 个环节教学方法的改进;以哈尔滨工业大学-伊顿联合实验室为依托,提出了具有电气工程教学特色的康奈尔大学笔记法思路。2018 年,将康奈尔大学笔记法思想融于自动控制原理双语教学中,突出图1 ~7 所示的教学体系模式,取得了较为理想的授课效果,15 人的大四授课对象中保研比例为93%,这在一定程度上验证了所提康奈尔大学笔记法教学思想的有效性。

