基于分段PD控制的振动基弹药传输机械臂轨迹跟踪控制

席宝成， 郭宇飞， 王志刚， 郝志强

(1.武汉科技大学 冶金装备及其控制教育部重点实验室,武汉 430081;2.武汉科技大学 机器人与智能系统研究院，武汉 430081)

主战坦克和自动火炮由于其优势火力和机动性能是现代军队不可或缺的重要组成部分。尤其因为现代大多数火炮和坦克装配了自动装弹机，这使得它们的优势更加明显。弹药传输机械臂作为坦克自动装弹机最重要的组成部分，取代了传统的人工搬运传送炮弹或手动推入炮膛的动作，一般安装在坦克车体内的弹药仓与炮尾之间，负责将弹药仓内的弹药协调到炮尾的待装填位置，也被称之为弹药协调器[1]。但是，现有的弹药传输机械臂还有很多的不足，比如控制精度低、可靠性差以及抗干扰能力不足等。

在实际使用中弹药传输机械臂的最大挑战为车体(基座)引发的随机振荡[2]。该振荡主要来源于随机激励的不规则路面与火炮的反冲击后坐力的激励，这两种情况均会导致弹药传输机械臂的底座发生剧烈的振动，由此产生的不确定扰动给自动装弹机的运动可靠度与操作安全性造成很大的影响。现有弹药传输机械臂系统大多采用传统的PID,PD控制策略，该控制策略已经被证明控制精度低，对车体振动、惯量变化等不确定因素的鲁棒性差，并且还存在控制性能依赖高控制增益、控制功率高、驱动器容易饱和等缺点[3]。为了解决这个问题，采用了定点的机械制动方式，虽然可以提高定位精度，但会增加一定的惯性冲击力，降低系统的可靠性。因此，对弹药传输机械臂的控制研究还处于初始阶段。

带有振动底座的弹药传输机械臂可以看作一种特殊类型的振动基座机械手(oscillation base manipulator, OBM)。OBM是安装在具有振动基座的机械系统的统称，如空间自由浮动机械手[4-5]、水下机器人[6-7]、海上起重机[8-11]、钻井船等都属于这一类系统。已有大量关于OBM的研究工作，为弹药传输机械臂的研究提供了丰富的经验。OBM通常根据振动的来源和起因分为两种主要类型，分别为基座固有结构柔性振动和外部干扰激励[12]。对于类型一，典型的相关应用是由刚性微机械手和柔性宏机械手组成的宏/微机械手[13]，它用于较大范围的操作任务，如核废料清理。微机械手的运动可以抑制宏机械手运动过程中造成的结构柔性振动。这类OBM面临的主要问题是振动阻尼问题，为此，已经开发了主动阻尼法，如输入整形技术[14-15]。针对宏/微机械手的运动控制问题，提出了多种控制策略，如基于神经网络的控制[16-17]、笛卡尔柔度控制[18]、监督控制[19]、模糊李雅普诺夫控制[20]等。此外，Lin等[21-22]也研究了此类型OBM，将其基本动力学简化为一种带弹簧的集中质量块，将动态模型通过奇异摄动技术解耦，通过混合控制实现振动阻尼，如模糊逻辑与PD控制相结合、分层模糊控制与监督控制相结合。然而，上述OBM的研究都基于基座振动可测量，从而建立反馈控制律来抑制这种振荡，这对于随机振动底座的弹药传输臂来说非常难以实现。对于第二种类型的OBM，最具代表性的应用是船用起重机及其它装置。这种类型的OBM通常在恶劣的海洋环境中工作，因此，安装的基座会受到海浪和海风造成的不可预测的倾斜和俯仰运动的干扰，从而会导致安装在船舶上的机械手产生较大的扰动和影响，如科氏力和作用在起重机上的离心力，这些非线性的变化使得机械手的控制和稳定问题变得十分棘手。此外，船舶的振荡频率有可能接近起重机系统固有频率的频率分量，导致意外的共振效应。为了解决这些问题，开发了几种控制方法，如基于李雅普诺夫的控制，主动补偿控制。Toda等[23-25]对发展此类OBM的运动控制有着重要贡献，建立了局部和全局坐标系下的通用动态模型，提出了基于H∞控制和滑模控制的鲁棒跟踪控制策略。但是，这些研究都建立在系统是线性的假设之上，并且基础振动的频率范围可以提前预测。

弹药传输机械臂基座振动问题属于第二类振动基座机械手。它的底盘振动主要来源于火炮反冲力和不平坦路面引起的外部激励，更为复杂。因此，从这个意义上说，基座振动的弹药传输机械臂与其它OBM有很大不同。首先，振荡频率范围无法准确测量或提前预测；此外，底座的振动表现为不规则干扰，不能通过主动补偿技术(如调节自身的执行器)来抑制。同时，弹药传输机械臂还面临另一个问题，随着现代军事要求不断地增强，武器的多元化和功能多样化更加重要，这就需要同一门火炮可能要发射有效载荷不同的炮弹来达到不同的军事目的，所以，弹药传输机械臂的控制必须满足系统的惯量参数的不确定性。因此，采用现有的针对上述对象的控制方法来解决基座振动的传输机械臂的控制问题是不现实的。

本文为了研究方便将弹药传输机械臂简化为升降部分和翻转部分的两自由度机械臂，研究其在随机振动以及有效载荷不确定情况下的轨迹跟踪问题。它兼有任意角度协调及抓取、推送弹药的功能。将基座振动的影响看作是机械臂所受的外部不确定扰动，采用Lagrange方程建立系统的不确定动力学方程。以此为基础，设计一种结合计算力矩法和分段线性反馈控制的不确定系统的轨迹跟踪控制器。该控制器属于滑模变结构控制器，本质上是一类特殊的非线性控制，其非线性表现为控制的不连续性，这种控制策略与其它控制的不同之处在于系统的“结构”并不确定，而是可以在动态过程中根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化，迫使系统按照预定的状态轨迹运动。由于滑动模态可以进行设计且与对象参数及扰动无关，使得变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辩识、物理实现简单等优点[26-27]。该控制器有以下几个特点：①控制对象为拉格朗日机械系统，控制器对系统的有界外部扰动具有很强的鲁棒性；②控制律表现为增益可变的比例微分控制，在动态过程中，控制器增益根据系统当时状态偏差以阶跃方式按设定规律作相应改变；③控制输入的大小有界[28-31]。最后基于MATLAB/Simulink软件对系统进行了运动仿真，对控制器的鲁棒性进行了验证。

1 弹药传输机械臂模型

1.1 三维模型与结构原理

弹药传输机械臂的三维模型如图1所示，结构原理如图2所示，它由安装架、升降部分与翻转部分组成。它的安装基座同时受到垂直上下振动、俯仰振动以及左右摇摆振动三个因素的影响。安装架固定在车体内，位于炮尾与弹药仓之间；升降部分采用双链传动，两主动链轮同轴固定且由同一电机驱动；升降部分固定在紧边链条上，可沿导轨上下滑动；翻转部分由电机通过减速器、转向器驱动，可360°翻转，兼有抓取与推送弹药的功能。

图1 弹药传输机械臂三维模型Fig.1 3D model of the ammunition transfer manipulator

图2 弹药传输机械臂的结构原理Fig.2 Structural model of the ammunition transfer manipulator

1.2 动力学建模

为了研究方便，将机械臂模型作如下简化：将其本体简化为一个升降部分加一个翻转部分。忽略升降部分链条传动部分的动力学特性和驱动回路的动态特性，将其简化为一个上下移动的质量块；不考虑翻转部分运动部件之间的摩擦与运动阻尼，将其简化为连接在升降部分的转动臂，如图3所示。图中，xOy为笛卡尔坐标系；B1,B2和B3分别为车体、自动装弹机的升降部分与翻转部分；C1,C2与C3分别为链条、升降部分与翻转部分的质心；L3为C2与C3之间的距离；yr1,yr2与θ3分别为各部分的相对位移或角位移。

图3 考虑车体俯仰振动的弹药传输机械臂的简化模型Fig.3 Simplified model of ammunition transmission manipulator considering pitch vibration of vehicle body

将车体振动的影响看作自动装弹机所受的不确定外部扰动，并且选取q=[q1,q2]T=[yr2,θ3]T为系统的广义坐标，则弹药传输机械臂的动力学模型为

(1)

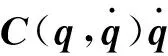
式(1)中各项的表达式分别为

其中，

式中：m1与m2分别为升降部分与翻转部分的质量；J为翻转部分等效到电机转轴上的转动惯量；g为重力加速度。

形如式(1)的动力学方程具有以下几个性质：

性质1惯量矩阵H(q)为正定对称矩阵，且上下有界，即对于任意一个向量λ，有

μ1λ2≤‖λTH(q)λ‖≤μ2λ2

式中：μ1,μ2为正实数;‖‖为矩阵或向量的欧式范数。

性质2存在常数g0>0，使得系统重力势能V(q)满足以下公式

性质3存在常数U0>0，使得广义控制力向量满足‖U‖≤U0。

性质4存在常数S0>0，使得广义外部扰动力向量满足‖S‖≤S0。

2 控制器设计与稳定性分析

2.1 计算力矩法

引入变量τ，S′，并定义

(2)

将式(2)代入式(1)，消去非线性项后，得

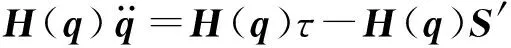
(3)

此外，根据矩阵H(q)的可逆性以及性质1和性质4，可以推断出S′是正定有界的，也就是说

(4)

由于H(q)的可逆性，进一步化解式(3)，得

(5)

定义

(6)

式中,qd为广义坐标的期望轨迹，是一个连续且二次可微的时变函数。将式(6)代入式(5)，得到误差方程

(7)

式中,e=qd-q。

如果不考虑车体振动的影响，即在S′=0的情况下，用经典调节原理中的方法便可以确定PD增益αk和βk的值。

2.2 基于分段线性反馈控制的控制律

如果考虑车体振动的影响，即在S′≠0的情况下，上述定常增益的PD控制器不再适用，重新选择增益αk和βk的值为

(8)

式中：u0为一个正实数；Wk为一组预先给定的正实数集

(9)

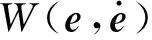
(10)

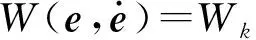
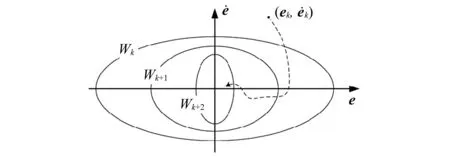
图4 系统状态图Fig.4 System state diagram

(11)

为了简单起见，我们选择W(t0)=Wk，在系统轨迹首次与(k+1)椭球面相交之前，保持当前Wk值；同样，Wk+1也将保持到系统遇到(k+2)椭球面为止，然后依次是Wk+2,Wk+3，…。这里我们定义了选择Wk作为tk时刻的值，选择Wk+1作为tk-1的值。

定义辅助控制变量

(12)

为误差系统式(7)的控制力向量，其满足条件

‖u‖≤u0

(13)

为了分析上述控制系统的运动稳定性，引入了一组李雅普诺夫函数

(14)

式中，εk为一组正数且满足以下条件

(15)

根据柯西不等式得

(16)

首先，我们来证明所提出的Lyapunov函数是正定的，根据式(16)和式(14)可写为

(17)

结合等式(15)与不等式(17)可得出

(18)

第二，由式(14)和式(16)的第二个不等式来求所提的Lyapunov函数的上界，可得

(19)

由式(15)，进一步化解式(19)，可得

(20)

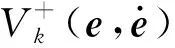
第三，我们将证明如下的关系

(21)

(22)

(23)

显然可见，基于式(22)和式(23)已然证明式(21)的合理性。

(24)

根据柯西不等式、式(21)和式(24)可以得到

(25)

因此，对于任意时刻t，可以得到

(26)

最后，来证明前面所提Lyapunov函数的导数是全局负定的。

(27)

然后，将式(7)和式(12)代入式(27)，可以得出

(28)

对于式(28)的最后一项，根据不等式(4)，可得

(29)

(30)

(31)

对于式(28)的第三项，根据柯西不等式可以得到

(32)

把不等式(31)和不等式(32)代入式(28)，最后可以得到

(33)

因此，根据表达式(15)，可以得到

(34)

然后，根据式(24)，不等式(33)可以进一步改写为

(35)

(36)

(37)

此外，我们将证明所提出的控制的有界特性，如性质3不等式所示。根据柯西不等式和不等式(20)，可以得出

(38)

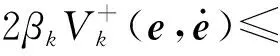
(39)

由此，性质3可证明成立。

于是，系统式(1)的广义控制力的完整表达式可以写为

(40)

由性质1、性质2、性质5与式(13)、式(40)可知

(41)

2.3 控制回路与计算流程

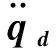
图5 控制回路Fig.5 Control loop

3 仿真计算

在这一节中，我们首先以某履带车辆为对象，基于ADAMS/ATV软件获得了其以40 km/h的恒定速度行驶在F级路面上的车体振动曲线。根据上文可知，弹药传输机械臂受到三种基座振动(垂直振动、俯仰振动、左右摇摆振动)的影响。根据前人的研究可知，俯仰振动对机械臂动力性能产生的影响最大，因此为了简单起见本文只关注俯仰振动。振动响应如图6所示。然后，选择系统各参数值如表1所示。

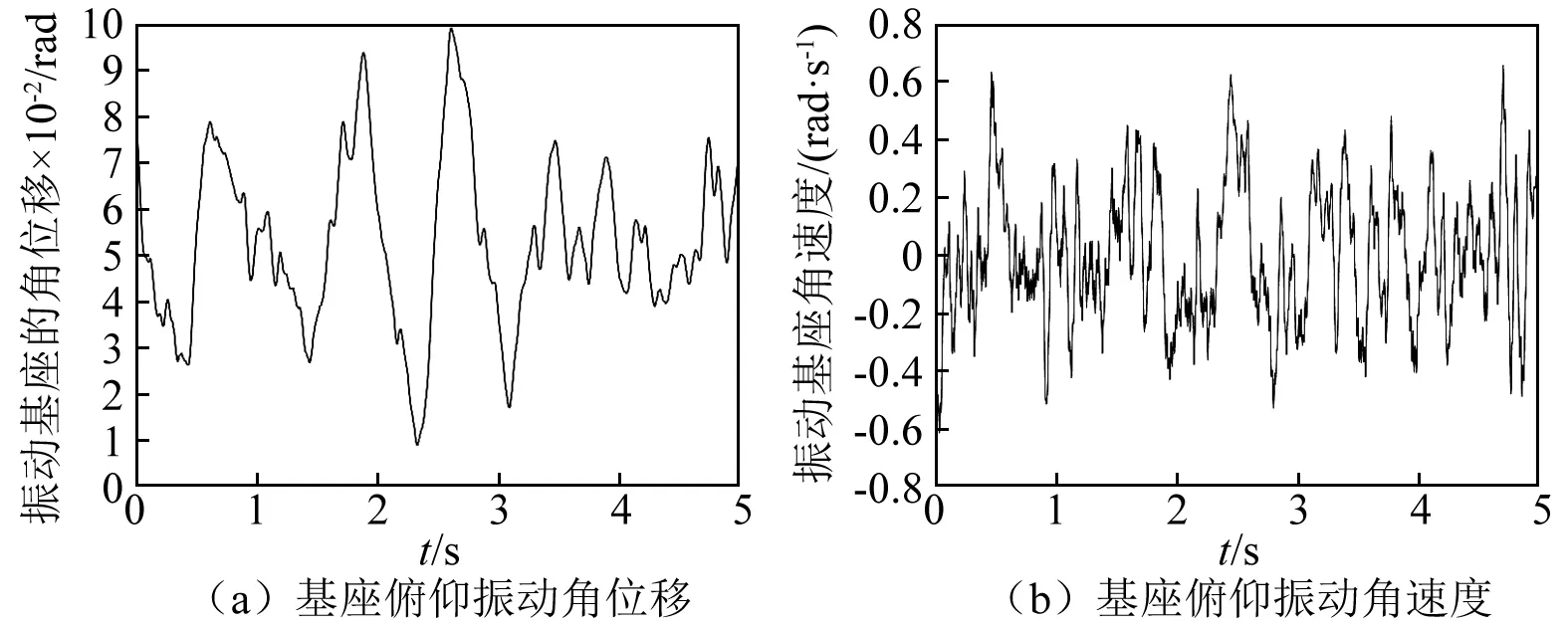
图6 基座俯仰振动响应曲线图Fig.6 Response curves of base pitch vibration

表1 系统仿真参数Tab.1 System simulation parameters

期望轨迹弹药转运机械手的跟踪控制的目的是实现火炮在俯仰过程中的自动装弹，因此配置机械手轨迹与火炮角度位置之间的关系非常重要。机械手与弹仓之间的几何关系如图7所示。其中B4和B5为炮筒和弹药仓，O4为炮筒的转动耳轴，θ为炮筒的仰角。图7中的其它符号含义与图3相同。基于上述关系，预先给出火炮装弹过程的运动情况，通过进一步的几何推导，可以得到比较理想的自动装弹机弹导曲线。

图7 弹药传输机械臂、弹仓和炮筒的几何关系Fig.7 The geometric relations among the transfer manipulator, magazine and gun barrel

仿真1为了验证本文所设计的控制器的有效性，对二自由度自动装弹机进行了运动仿真，仿真时间设置为5 s，相应的仿真结果如图8所示。可见，本文所设计控制器在俯仰振动的作用下表现出良好的跟踪性能，弹药传输机械臂升降部分与翻转部分位移曲线(实线)在很短的时间里就实现了对期望轨迹(虚线)的有效跟踪，并且两部分的稳态误差都很小，升降部分小于0.000 1 m，翻转部分小于0.000 3 rad。这已经非常好的达到了控制要求的精度，如图8(a)和图8(c)所示。不仅如此，在位置精度很高的前提下，机械臂的运动速度同样也能很好跟随期望的速度曲线，由图8(c)和图8(d)所示。为了更清楚地显示所提控制器的性能和分段特性，在图9(a)中显示了上述仿真的位移响应误差，可以看出两个部分的误差都在0.63 s左右趋近于0；在图9(b)给出了控制系统增益的选择系数k,可见k值随着系统的变化呈现出分段特性。图10(a)和图10(b)为比例增益βk和微分增益αk的曲线图，由局部放大图明显可以看出两者都呈现出分段特性；图10(c)和图10(d)为误差系统控制输入，即分段控制。由此可见，本文所提的分段控制器对基座振动状态下的弹药传输机械臂的位移表现出了良好的控制性能，同时也对速度有很好的跟随性。根据以上所述，本文所提的控制器具有良好的鲁棒性。

图8 标称惯量系统跟踪轨迹响应曲线Fig.8 Tracking trajectory response curves of nominal inertia system

图9 位移误差与选择系数k曲线Fig.9 Position error and selection coefficient k curves

图10 增益响应和控制输入曲线Fig.10 Gain response and control input curves

仿真2为了验证控制器对传输机械臂有效载荷不确定性的鲁棒性，进行了另外一组仿真。由于有效载荷属于旋转部分，因此对惯性以及旋转部件的质量分别增加了20%(惯量正偏差)和减少了20%(惯量负偏差)，其它参数保持不变，仿真结果如图11所示。惯量正偏差和惯量负偏差的响应分别用全点线和点划线表示。可以看出，惯量不确定性对控制性能仅在跟踪时间上有微小的差别。与预期的情况一样，在惯量正偏差时，系统达到有效跟踪的时间比标称惯量所用时间晚了0.33 s，而负惯量偏差则快了0.32 s。除此之外，系统的稳态误差与跟踪状态并没有什么区别，这进一步证明了该控制器具有良好的鲁棒性。

仿真3为了更好的证明本文所提控制器的良好性能，进行了一组对比仿真实验。在保证系统参数不变的情况下，采用传统的PD控制代替本文的分段线性反馈控制器，比例增益与微分增益分别为2 400和50。仿真结果如图12所示。由图11(a)可以明显的看到上升部分的位移响应曲线在整个跟踪过程中产生较大的超调并且稳态误差达到了0.02 m；翻转部分同样具有很大的超调，而且跟踪响应很不稳定。由此可见，在传统的PD控制条件下，基座振动的弹药传输机械臂无法达到需要的控制精度。综上所述，可以说明本文所设计的控制器比一般基于恒定增益PD的控制方法具有更好的控制效果和鲁棒性。

图11 惯量参数不确定系统跟踪轨迹响应曲线Fig.11 Tracking trajectory response curves of uncertain inertia parameter system

图12 PD控制系统跟踪轨迹响应曲线Fig.12 Tracking trajectory response curves of PD control

4 结 论

本文以现代军用火炮和主战坦克的自动装弹机为研究背景，研究了在车体(底座)随机振动以及有效载荷不确定的情况下，弹药传输机械臂的轨迹跟踪控制问题。在研究过程中将机械臂简化为升降部分和翻转部分两部分，将基座的振动看作外部不确定扰动。基于分段线性反馈控制算法与计算力矩法相结合的方法设计鲁棒控制器，为带有基座振动的机械臂控制问题以及自动装弹机的随动装填提供了新的解决方案。该控制器表现为增益可变的比例微分控制，在动态过程中，控制增益根据系统实时状态偏差以阶跃方式按设定规律作相应改变，随着系统状态与期望状态误差逐渐趋近于零，增益处于动态平衡状态，且控制力始终满足给定约束。采用龙格库塔法在MATLAB/Simulink环境下进行数值仿真，仿真结果显示，所设计控制器能够克服车体在振动作用下以及有效载荷不确定情况下的轨迹跟踪问题，具有良好的鲁棒性。