大型浮筏姿态及弹性变形控制算法研究

秦文政， 施 亮

(1. 海军工程大学 振动与噪声研究所，武汉 430033； 2. 船舶振动噪声重点实验室，武汉 430033)

将气囊隔振器应用于浮筏隔振系统，可以显著提高浮筏隔振效果，但也会带来筏架姿态平衡欠佳的问题[1]。目前，国内学者已经在浮筏姿态平衡控制[2-5]、轴系对中控制[6-9]等方面开展了大量研究工作，并取得了较好的控制效果。

然而，随着浮筏气囊隔振系统趋于大型化[10-11]，其筏体结构刚度不可避免的降低。在外界扰动作用下，筏架不仅会偏离平衡位置，还会产生较大的弹性变形，造成筏上设备之间、设备与外接管路之间产生较大的相对位移，严重时容易超出其许用位移，危及设备运行安全。此外，筏架的弹性变形还可能影响主机与轴系的对中安全性，如图1所示。因此，对大型浮筏气囊隔振系统而言，不仅需要控制筏架姿态平衡，还必须考虑筏架弹性变形的控制问题。

图1 某大型浮筏气囊隔振系统示意图Fig.1 Diagram of a large floating raft air spring isolation device

上述文献中的气囊控制方法对结构刚度较大的中小型筏架姿态平衡问题具有理想的控制效果，但尚未涉及大型筏架弹性变形的控制问题。

本文对大型浮筏气囊隔振系统筏架姿态和弹性变形控制问题进行了研究。建立了某船舶浮筏隔振装置柔性筏架响应模型，并在此基础上提出了一种基于气囊压力参数识别的控制方法，最后在试验平台上进行试验。试验结果表明：该方法不仅可以控制筏架姿态平衡，还能够有效抑制筏架弹性变形，并且具有较高的控制精度。

1 柔性筏架响应模型

以某船舶大型浮筏隔振装置为研究对象如图2所示，建立了该装置的柔性筏架响应模型。其中，筏体尺寸为10.0 m×6.5 m×2.0 m；在筏架两舷侧均匀布置20个气囊隔振器；另布置6个位移传感器用于监测筏架姿态和弹性变形。

图2 浮筏气囊隔振系统示意图Fig.2 The sketch of floating raft air spring isolation device

建立以系统重心为原点的总体坐标系O-XYZ和以各气囊重心为原点的局部坐标系oi-xiyizi。根据文献[12-13]，可得到浮筏刚体静力学模型，其静力学方程表达式为

Kxc=F

(1)

式中：K为系统总体刚度矩阵；xc为系统重心在O-XYZ坐标系中的平动位移和绕各坐标轴的转动角度；F为系统受到的外力。

气囊在额定高度附近工作时，其有效面积Se可近似为常数[14]，此时气囊承载变化ΔF与压力变化ΔP的关系可表示为

ΔF=ΔP·Se

(2)

由式(1)和式(2)经坐标变换可得到任一气囊充/放气时刚体筏架响应位移dij。

在浮筏刚体静力学模型的基础上，针对筏架弹性变形的特点，引入筏架响应修正系数矩阵，表达式为

(3)

式中：Ac，Af分别为充气、放气条件下筏架响应修正系数矩阵；aij为第i个气囊在j号传感器处筏架的响应修正系数，表达式为

(4)

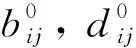
由式(1)～式(4)可求得任一气囊调整后柔性筏架响应理论值

(5)

综上，依据此柔性筏架响应模型，可预判任一气囊充/放气操作后筏架的调整效果。

2 控制性能指标

2.1 筏架弹性变形表示方法

筏架弹性变形是相对而言的。外界扰动作用下筏架产生的实际位移包含“刚体位移”和“弹性变形位移”，两者相互耦合，难以完全分离。因此，研究筏架弹性变形问题时，必须选择一个合适的参考基准。

通常，气囊控制系统将筏架四角高度作为筏架姿态平衡的控制参数，会优先将其位移控制在精度指标范围内，所以将1#～4#传感器位移作为筏架弹性变形的参考基准。

5#，6#传感器处筏架的弹性变形位移可用其实际位置到参考基准的距离表示，如图3所示。

图3 筏架弹性变形表示方法Fig.3 Expression method of elastic deformation of raft

以5#位移传感器为例，该处筏架弹性变形位移Δx5可表示为

(6)

式中，x1，x3，x5分别为1#，3#和5#位移传感器读数。

2.2 控制性能指标函数

大型筏架由于设备工况多，局部载荷变化大，导致筏架弹性形态复杂，难以通过气囊压力调整使所有位移参数同时收敛。

为避免系统振荡甚至不收敛，在控制性能指标函数Hs中引入动态权重系数a，以提高控制算法对筏架不同弹性形态的适应性。筏架姿态及变形控制性能指标函数Hs可定义为

(7)

式中： |xj|为各位移传感器读数的绝对值，反映了筏架偏离理想姿态位置的大小；a为动态权重系数，用于提高控制算法对复杂工况的适应性，初始值为1，取值范围为[0,1]；ε为筏架控制精度，由于ε关于筏架理想姿态位置对称分布，所以式(7)中取ε/2。

显然，当Hs<1时，筏架在控制精度ε范围内，此时算法收敛。反之，若Hs>1并且最近两次筏架调整效果不明显，表明调整气囊压力已经难以改善筏架姿态及弹性变形，此时需要减小a值使筏架快速收敛，避免系统振荡。

3 筏架姿态及弹性变形控制算法

3.1 主控制器设计

筏架姿态及弹性变形控制原理如图4所示。假定控制系统将进行第k+1次调整，其调整步骤如下：

图4 筏架姿态及弹性变形控制原理图Fig.4 Flow diagram of attitude and elastic deformation control for raft

步骤1判断动态权重系数a是否需要调整。以第k次调整后各位移传感器参数变化量绝对值的最大值表示第k次筏架的调整效果

(8)

步骤2判断气囊是否需要调整。若Hs<1则表明筏架在控制精度指标ε范围内，此时不需要调整气囊；反之，进行下一步。

步骤3选择需要调整的气囊编号。

步骤4根据模糊控制规则确定气囊充放气时间。

步骤5预判筏架调整效果。

步骤6对筏架姿态和弹性变形进行调整。

3.2 气囊选择策略及预判

假设筏架处于理想姿态位置时，各位移传感器读数为0并且各气囊均处于额定状态，则气囊高度偏差也可以反映筏架偏离理想姿态位置的大小。

以气囊额定工作高度为零点，当筏架偏离理想姿态位置时，气囊高度偏差为

Δh=h-H

(9)

式中： Δh为气囊高度偏差，可由筏上各位移传感器参数线性差值得到；h为气囊实际工作高度；H为气囊额定高度。显然，当筏架位于理想姿态位置上方时，Δh为正值；反之，Δh为负值。

大型筏架姿态和弹性变形控制的实质是通过调整气囊压力来减小气囊的高度偏差。但大型浮筏气囊数量多，气囊工作高度之间的耦合作用也较强，所以对某个气囊进行充、放气操作时，筏架其他位置气囊的工作高度也发生变化，如图5所示。

图5 气囊耦合作用的影响Fig.5 Influence of air spring coupling

显然，充气过程中，若两个气囊的高度偏差Δh相同，则控制系统应当优先对其中压力较小的气囊实施充气操作；而放气过程中，若气囊高度偏差Δh相同，则控制系统应当优先对其中压力较大的气囊进行放气。

因此，可以利用气囊压力参数对气囊高度偏差进行定性识别，以减小气囊耦合作用的影响。

(10)

图5展示了筏架刚体假设条件下气囊耦合作用的影响，然而大型筏架柔性较大，其弹性变形复杂，大大增加了气囊调整时其他气囊高度偏差变化的复杂性，可能会使筏架不收敛。

因此，为提高气囊调整的准确性，需要对筏架调整效果进行预判，并根据预判结果对气囊编号选择进行修正。引入修正系数χ，得到气囊编号选择判据为

Qi=λi·χi·Δhi

(11)

式中：Qi为气囊广义高度偏差，用于判断气囊调整的优先级，Qi绝对值越大，则气囊调整优先级就越高；λi为通过识别气囊压力参数得到的修正系数，用于减小气囊耦合作用的影响；χi为根据筏架预判结果得到的修正系数，用于提高气囊编号选择的准确性，χi初始值为1，取值范围为[0,1]； Δhi为气囊高度偏差。

根据式(11)选择优先级最大的气囊进行调整，然后由模糊控制规则表确定气囊充放气时间，最后依据式(5)预判筏架的响应位移。

定义判据Jy来表示筏架调整是否有效

(12)

显然，不论充气还是放气过程，当两者符号相反，即Jy<0时，表明此次调整有效； 反之，需要减小χi重新选择气囊编号。根据试验平台系统调试结果，取χi的减小幅值为0.2。气囊编号选择及预判流程如图6所示。

图6 气囊选择及预判流程图Fig.6 Flow diagram of air spring selection and prediction

4 试验研究

本文试验装置为某船舶大型浮筏气囊隔振装置2∶1缩比试验平台，如图7所示。其中，筏架尺寸为5.5 m×3.5 m×0.2 m；沿筏架两舷侧均匀布置20个气囊隔振器；另布置6个位移传感器，位置分布与图2相同；通过一套液压伺服加载装置调整浮筏载荷。

图7 浮筏气囊隔振装置试验平台Fig.7 Floating raft air spring isolation device test platform

根据相关技术标准，取筏架姿态及弹性变形控制精度ε为-1～+1 mm。试验前手动调整气囊使筏架偏离平衡位置约±3 mm，然后分别采用刚体浮筏控制算法和本文控制算法对筏架进行调整。

其中，刚体浮筏控制算法主要通过筏架四角高度控制筏架姿态平衡，控制目标是将1#～4#位移传感器参数控制在精度指标范围内；而本文控制算法是在控制筏架姿态平衡的基础上尽可能地抑制筏架的弹性变形，控制目标是尽量将1#～6#位移传感器参数同时控制在精度指标范围内。

充气调整过程试验结果如图8所示，调整后筏架弹性变形位移如表1所示。

图8 筏架调整试验曲线Fig.8 Raft adjustment test curve

表1 筏架弹性变形位移试验值Tab.1 Test values of elastic deformation displacement of raft mm

从图8和表1可知，采用刚体浮筏控制算法时，经14次调整，筏架姿态可被控制到-1～+1 mm，此时筏架最大变形位移为1.75 mm；采用本文控制算法时，经13次调整，筏架姿态可被控制到-1～+1 mm，再经过2次调整，筏架姿态可被控制到-0.5～+0.5 mm，调整后筏架最大变形位移为0.74 mm。对比可知，充气调整时，本文控制算法能有效抑制筏架弹性变形，并且具有较高的控制精度。

放气调整过程试验结果如图9所示，调整后筏架弹性变形位移如表2所示。

图9 筏架调整试验曲线Fig.9 Raft adjustment test curve

表2 筏架弹性变形位移试验值Tab.2 Test values of elastic deformation displacement of raft mm

从图9和表2可知，采用刚体浮筏控制算法时，经70次调整，筏架姿态可被控制到-1～+1 mm，此时筏架最大变形位移为1.99 mm；采用本文控制算法时，经50次调整，筏架姿态即可被控制到-1～+1 mm，调整后筏架最大变形位移为1.16 mm。对比可知，放气调整时，本文控制算法调整速度较快，并且能有效抑制筏架弹性变形。

综上，试验结果表明本文控制算法不仅可以控制筏架姿态平衡，还能够有效抑制筏架弹性变形，并且控制精度较高。

5 结 论

本文研究了大型浮筏气囊隔振系统筏架姿态和弹性变形的控制问题。针对大型浮筏的特点，建立了柔性筏架响应模型并用于预判筏架的调整效果，同时提出了一种基于气囊压力参数识别的控制方法，并将筏架预判结果融入到该控制方法中，实现了大型浮筏姿态和弹性变形的自动控制。试验结果表明：该控制方法可以控制筏架姿态平衡并有效抑制筏架弹性变形，同时还具有较高的控制精度。