矿用铰接式车辆路径跟踪控制研究现状与进展

白国星，罗维东，刘 立，孟 宇，顾 青，李凯伦

北京科技大学机械工程学院，北京 100083

✉通信作者，E-mail: myu@ustb.edu.cn

采矿作业环境恶劣，自动化已经成为世界矿业的主要发展趋势，矿用车辆的自主行驶是采矿自动化的重要研究方向. 在矿用车辆中，铰接式车辆（可简称为铰接车）采用前后车体折腰的形式完成转向. 因此铰接式车辆具有较为特殊的运动学、动力学特性，其路径跟踪控制也成为了矿用车辆自主行驶的一个热点和难点. 2005 年Dragt 等对铰接式铲运机的自动化进行了综述，回顾了铰接式车辆的运动学模型、路径跟踪控制方法等路径跟踪控制关键研究点的研究进展[1]. 而在最近的十五年中，铰接式车辆的路径跟踪控制研究又有了一些新的发展动态.

在数学建模方面，由于运动学模型日益难以满足铰接式车辆路径跟踪控制的需求，所以研究者们逐渐将注意力集中到了动力学模型的研究.路径跟踪控制方法也迎来了发展的高潮，研究者们基于不同的控制方法提出了多种高性能的路径跟踪控制器. 基于上述发展趋势，从铰接式车辆数学模型和铰接式车辆路径跟踪控制方法两个方面，阐述了矿用铰接式车辆路径跟踪控制研究的现状和进展. 在此基础上，总结了不同数学模型和控制方法对路径跟踪控制性能的影响，提出了进一步提高路径跟踪控制精确性和安全性的研究思路，以图为矿用铰接式车辆的路径跟踪控制提供技术参考.

1 铰接式车辆数学模型

在Dragt 等的工作中，铰接式车辆的模型分为无侧滑模型、有侧滑模型和误差模型[1]. 不过无侧滑模型和有侧滑模型均属于运动学模型的范畴，而误差模型通常是基于运动几何关系推导获得的运动学模型衍生物. Dragt 等没有回顾关于铰接式车辆动力学模型的研究，但是该模型对路径跟踪控制意义较大. 综上可将铰接式车辆的模型研究分为运动学模型和动力学模型两类.

（1）运动学模型.

根据Dragt 等的工作，可以将关于铰接式车辆运动学模型的研究成果分为两类，即无侧滑模型和有侧滑模型.

A. 无侧滑模型

关于无侧滑铰接式车辆运动学模型的研究工作历史较为悠久. Hemami 和DeSantis 参考前轮转向车辆的运动学模型建立了早期的无侧滑铰接式车辆运动学模型[2-4].

如果铰接角定义为后车体航向减去前车体航向之差，即γ=θr-θf，该模型在全局坐标系下的一般形式可以列为：

式中，x 为横坐标，y 为纵坐标，θ 为航向角，v 为纵向速度，l 为车桥到铰接点的距离，下标f 表示前车体，下标r 表示后车体，δ 表示铰接点速度矢量与前车体之间的夹角，γ 为铰接角.

在较早的铰接式车辆路径跟踪控制中，该模型得到了较为广泛的应用[5-7]. 但是由于该模型中存在中间变量tan δ，计算过程复杂且映射关系不够直观，所以研究者们对该模型又做了一些改进.将式（1）中的tan δ 消去，并用ωγ表示铰接角速度，即可获得该运动学模型的另一种形式：

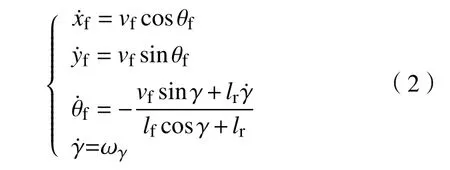
1999 年Altafini 给出了与式（2）相近的铰接式车辆运动学模型[8]，但是没有给出具体的推导过程. 而且在Altafini 的模型中，模型的输出状态是后桥中心的状态，但是在铰接式车辆的路径跟踪控制中，很少采用以后桥中心状态作为输出状态的运动学模型. 2001 年Corke 和Ridley 给出了形如式（2）的铰接式车辆运动学模型的详细推导过程[9]. 2019 年白国星等基于非完整约束条件提出了一种更加简便的铰接式车辆运动学模型推导方法，并得到了相同的运动学模型[10].

该模型还有一个变体，如果将铰接角定义为前车体航向减去后车体航向之差，即 γo=θf-θr，最终得到的模型为：

式（2）和式（3）之间的区别仅为铰接角正方向的定义，两个模型的特性完全相同.

在行驶速度较低时，这种运动学模型的精度较高，而铰接式车辆的多数工况都不需要高速行驶，所以该模型的应用十分广泛，很多研究者基于这种模型设计了路径跟踪控制器[11-20]. 因此该模型可称为铰接式车辆的经典运动学模型.

B. 有侧滑模型

铰接式车辆的运动学模型中，有侧滑模型的出现时间略晚于无侧滑模型. 1997 年Scheding 等参考前轮转向车辆的运动学模型提出了考虑侧滑的铰接式车辆运动学模型[21]，并证明了相比无侧滑模型，有侧滑模型与实车测试的数据更加接近[22].2011 年Nayl 等在形如式（3）的经典运动学模型中加入了侧偏角，建立了新的有侧滑模型[23]，其后基于该模型设计了用于铰接式车辆的路径跟踪控制器[24-26].

在有侧滑模型中，需要将侧偏角作为已知量输入运动学模型. 在作为被控对象验证控制算法时，该模型相对无侧滑模型更加接近实际工况. 但是由于运动学模型中不考虑侧向加速度，有侧滑模型无法预测铰接式车辆未来的侧滑情况. 在作为参考模型设计控制器时，如果铰接式车辆的纵向行驶速度较低，该模型相对无侧滑模型对控制精确性的提升极为有限，而如果铰接式车辆的纵向行驶速度较高，误差中将包含较多侧滑导致的成分，控制器会通过增大横摆角速度来消除侧向速度带来的额外误差，从而进一步增大侧向加速度，导致铰接式车辆侧向速度的进一步增大，最终发生危险. 因此从理论上来看，有侧滑铰接式车辆运动学模型更加适合作为仿真系统中的被控对象，而在作为路径跟踪控制器的参考模型时存在增大侧滑趋势的倾向.

总而言之，在运动学模型层面，经典铰接式车辆运动学模型虽然无法将轮胎侧滑等现象纳入考虑，但是由于其结构简单，在行驶速度较低时精确性尚可，所以在铰接式车辆的路径跟踪控制中，该模型的应用较为广泛.

（2）动力学模型.

由于基于运动学模型的控制器无法有效处理侧滑问题，所以目前铰接式车辆的自动行驶控制通常仅在低速工况下运行. 但是铰接式卡车等矿用车辆也有高速运行的需求，所以铰接式车辆的动力学模型也是铰接式车辆路径跟踪控制领域中的一个研究热点.

在铰接式车辆动力学模型的研究工作中，虚拟样机和数学模型是两个主要研究方向. 研究虚拟样机的目的通常是为悬架系统、差速系统的设计提供参考[27-29]，而在针对路径跟踪控制的研究工作中，虚拟样机通常仅作为用于测试控制方法的被控对象，所以本文主要针对铰接式车辆数学模型的研究工作进行回顾. 铰接式车辆动力学模型的数学建模方法可以分为两类，即牛顿-欧拉法和拉格朗日法，其中基于牛顿-欧拉法的铰接式车辆动力学模型较为常见.

A. 基于牛顿-欧拉法的动力学模型

基于牛顿-欧拉法的建模研究，还可以根据模型的自由度继续细分，分为二自由度、三自由度、四自由度和多自由度模型. 二自由度的铰接式车辆模型较为罕见，仅He 等在其论文中有所提及[30]，而且在该论文中二自由度模型仅作为四自由度动力学模型的对照，目前也未见其他学者对二自由度模型进行深入研究.

铰接式车辆的三自由度模型较为常见，按照自由度的选择，该模型也可以分为两类. 其中最常见的一类是选择前后车体的横向速度和横摆角速度作为输出状态的模型，由于前后车体的横向速度存在耦合，所以其自由度为三，这种模型也常被叫做原地转向模型[31-36]. 另一类是将铰接角视为固定值的动力学模型，在这种模型中前后车体被视为刚性连接或弹簧阻尼连接，其输出状态为前车体纵向速度、横向速度和横摆角速度，这种模型也被叫做稳态转向模型[37-47]. 上述模型常用于铰接式车辆行驶稳定性等领域的研究，而铰接式车辆的路径跟踪控制需要同时对前车体的纵向速度、横向速度、横摆角速度和后车体的横摆角速度进行控制，所以三自由度模型对于铰接式车辆路径跟踪控制不具有完备性.

铰接式车辆四自由度动力学模型的研究也具有较长的历史，周国建在1992 年即采用牛顿-欧拉法建立了四自由度铰接式车辆转向动态数学模型[48-49]. 1997 年DeSantis 在其论文中给出了相似的模型[4]. 此后He 等[30]、Azad[40,50]、Dou 等[51-52]也提出了四自由度铰接式车辆动力学模型. 上述四自由度动力学模型能够完备地反映铰接式车辆前车体纵向速度、横向速度、横摆角速度和后车体横摆角速度等状态，原则上可以满足铰接式车辆路径跟踪控制的需求. 不过在这些研究成果中，文献[48]～[49]只考虑了铰接式车辆前、后车体在铰接角发生变化时的瞬态转向特性，而忽略了铰接角不变时前、后车体受纵向力和横向力作用的稳态转向. 文献[11], [30], [40], [50]～[52]则试图通过将液压转向机构简化为弹簧阻尼结构来解决这个问题，但是简化后模型的特性是内力矩随铰接角近似线性变化，而实际的铰接式车辆内力矩是由纵向力、横向力以及车身加速度等状态决定的变量. 因此虽然四自由度模型在理论上可以满足路径跟踪控制的需求，但是现有模型仍不足以作为铰接式车辆路径跟踪控制的理论基础.

已知的多自由度铰接式车辆动力学模型包括Azad 提出的五自由度模型和七自由度模型[40]，以及Gao 等提出的十二自由度模型[53]. 对于路径跟踪控制而言，多自由度模型包含了过多非控制目标的状态变量，而多个变量之间的耦合关系可能会引起控制器优化函数非凸等问题，因此这种模型通常更适合作为测试控制方法的被控对象. 不过多自由度模型处理瞬态转向与稳态转向之间关系的方法，可以被移植到四自由度模型的建模研究中，从而帮助建立能够满足铰接式车辆自动行驶控制需求的动力学模型.

B. 基于拉格朗日法的动力学模型

基于拉格朗日法的铰接式车辆动力学模型较为少见，刘刚等[54]、葛强胜等[55-56]和Alshaer 等[57]分别基于该方法建立了铰接式车辆的动力学模型. 通过拉格朗日法建立的模型计算量较大，不利于作为路径跟踪控制的参考模型，因此基于拉格朗日法的铰接式车辆动力学模型通常仅作为被控对象，用于验证控制器的性能.

总而言之，在动力学模型层面，基于牛顿-欧拉法的四自由度铰接式车辆动力学模型在理论上较为适合作为路径跟踪控制的参考模型. 但目前存在的四自由度模型还存在无法同时反映瞬态转向特性和稳态转向特性的问题，因此还需参考多自由度模型的建模方法继续改进，才能满足铰接式车辆路径跟踪控制的需求.

2 铰接式车辆路径跟踪控制方法

在实现矿用铰接式车辆自主行驶的过程中，需要运用实时通信、环境感知、决策规划、路径跟踪等技术. 其中实时通信、环境感知、决策规划是可以用于不同领域的共性技术，而路径跟踪是自主行驶系统的最终实现手段，也是自主行驶系统的核心技术. 矿用铰接式车辆的路径跟踪，即通过对巷道环境信息和车身姿态信息进行实时感知，控制铰接式车辆的车速和转向，从而在保证安全的前提下，使铰接式车辆沿着规划决策系统给出的参考路径行驶.

根据日常的驾驶经验，如果驾驶员将目光适当前移，偏离预定路线的情况将大幅减少. 目光前移的动作可以称为预瞄，其本质是在驾驶员的控制行为中加入预定路线上的前馈信息. 由于引入前馈信息可以有效提高铰接式车辆路径跟踪控制的精确性，因此可以按照有无前馈信息对铰接式车辆路径跟踪控制方面的研究成果进行分类.

（1）无前馈信息的路径跟踪控制方法.

无前馈信息的路径跟踪控制方法还可以细分为有模型控制方法和无模型控制方法.

A. 有模型控制方法

常用于铰接式车辆路径跟踪控制的有模型控制有两类，分别是反馈线性化控制和最优控制（Optimal control）.

a. 反馈线性化控制

反馈线性化控制在铰接式车辆路径跟踪控制中较为常见，该方法通过将铰接式车辆的运动学模型推导为误差模型，然后基于状态反馈控制解算消除各误差值所需的控制输入，从而获得能够使移动装备跟踪参考路径的控制律. 从1996 年直到2019 年， Hemami 和Polotski[58-59]、 Polotski[2-3]、DeSantis[4]、Petrov 和Bigras[5]、Bigras 等[6]、Ridley和Corke[11]、Marshall 等[12]、Zhao 等[13]、Bian 等[16]和Dekker 等[20]等先后使用该方法研究了铰接式车辆的路径跟踪控制.

根据上述研究工作可知，基于反馈线性化控制的路径跟踪控制器可以有效控制铰接式车辆跟踪参考路径. 但是这类控制方法在跟踪不同参考路径时需要设置相应的控制器参数来保证控制效果，所以在参考路径较为复杂时难以保证路径跟踪控制的效果. 这个特点导致基于反馈线性化控制的铰接式车辆路径跟踪控制器在实际应用中受到了诸多限制.

b. 最优控制

最优控制与其他反馈控制的区别主要在于其镇定函数为运动状态等性能指标的泛函. 通过求解泛函的极大值或极小值，即可获取某一个或某几个性能指标的最优控制律. 镇定函数为二次型的最优控制，即LQR（Linear quadratic regulator）控制，Meng 等[19]根据这种控制方法设计了用于铰接式车辆的路径跟踪控制器. 相对反馈线性化等控制方法，LQR 具有设计简便、鲁棒性较强等优势.但是由于缺乏前馈信息，传统的LQR 路径跟踪控制器在参考路径存在较大幅度的曲率突变时仍然性能不佳.

B. 无模型控制方法

常用于铰接式车辆路径跟踪控制的无模型控制方法有三类，分别是PID（Proportion integral differential）控制、滑动模态控制（Sliding mode control，SMC）和智能控制.

a. PID 控制

PID 是最为经典的无模型反馈控制方法，其设计过程简便，适合用于工程开发，因此PID 控制在铰接式车辆路径跟踪控制中的应用十分广泛. 但是由于控制性能受参数影响较大，目前研究者们通常将PID 控制器作为改进基础或对照基准. 近年来的研究成果中，Alshaer 等采用PID 控制作为模糊控制（Fuzzy control）的对照组，研究了这两种控制器在铰接式车辆路径跟踪控制中的性能差异[57].

b. 滑动模态控制

滑动模态控制也就是变结构控制（Variable structure control，VSC），通常也可以简称为滑模控制. SMC 是一种出现于20 世纪50 年代的特殊非线性反馈控制，其原理是基于系统的状态，动态改变控制系统的结构，迫使系统按照预先设定的状态轨迹运动. SMC 在路径跟踪控制中的应用较为广泛，赵翾等[14]、Nayl 等[60]基于这种方法设计了铰接式车辆路径跟踪控制器. 由于SMC 的设计与被控对象的模型无关，所以具有响应速度快、鲁棒性强等优点. 但是SMC 也具有固有缺陷，当状态轨迹到达滑模面后，控制量可能会产生颤动[61].

c. 智能控制

智能控制的定义是具有学习功能、适应功能、组织功能等能力的新型控制方法，是人工智能和自动控制学科交叉产生的最新成果. 目前已经出现了多种智能控制方法，其中较为重要的分支包括模糊控制、神经网络（Neural network，NN）和遗传算法（Genetic algorithm，GA）[62]，这些智能控制方法本身属于无模型控制，但是也可以和其他有模型控制或无模型控制结合，形成复合控制器，从而提高控制性能.

在铰接式车辆的路径跟踪控制中，Sasiadek 和Lu 结合反馈线性化控制与模糊控制建立了控制器[7]，Tan 等基于PID 控制的框架设计了模糊控制器[17]，Alshaer 等则基于误差设计了单独的模糊控制器[57]. 这些工作证明了模糊控制性能优于反馈线性化控制、PID 控制等作为改进基础或对照基准的控制方法. 但是也表明模糊控制的性能受限于控制系统的结构.

神经网络也被称为人工神经网络（Artificial NN，ANN），在路径跟踪控制中较为常见的神经网络包括BP（Back propagation）神经网络、径向基（Radial basis function，RBF）神经网络、强化学习（Reinforcement learning，RL）神经网络等. 在铰接式车辆的路径跟踪控制中，邵俊恺等提出了基于RL-PID 的控制器[15]. 与模糊控制一样，神经网络控制虽然能改进控制性能，但是这种控制方法的性能也取决于控制框架.

遗传算法是一种计算智能，常用于PID、LQR、SMC 等控制方法中的参数自适应调整. 孟宇等采用GA 优化了LQR 控制器的参数，提高了铰接式车辆的路径跟踪控制性能[19]，但是GA 仍然只能对控制方法的某些性能指标进行改进，无法弥补控制方法机理方面的不足.

总而言之，受限于前馈信息的缺乏，所有无前馈信息的路径跟踪控制方法均无法有效解决参考路径存在较大幅度的曲率突变时误差较大的问题. 而对于铰接式车辆等工作环境较为狭窄的移动装备，跟踪存在较大幅度曲率突变的参考路径是十分常见的工况，因此无前馈信息的控制方法在铰接式车辆路径跟踪控制中的应用受限颇多.而就无前馈信息的控制方法本身而言，模糊控制、神经网络等智能控制方法可以有效改善其他控制方法的性能，所以这些控制方法在铰接式车辆路径跟踪控制中仍然具有较为广阔的应用前景.

（2）有前馈信息的路径跟踪控制方法.

有前馈信息的路径跟踪控制方法可以再细分为两类，前馈-反馈（Feedforward-Feedback）控制和模型预测控制.

A. 前馈-反馈控制

在路径跟踪控制中，前馈-反馈控制即将参考路径上的前馈信息引入无前馈信息的反馈控制器的控制方法，上文中提到的反馈线性化控制、最优控制、PID 控制、SMC 和智能控制均可作为前馈-反馈控制中的反馈控制方法. 在乘用车等移动装备的路径跟踪控制中，前馈-反馈控制已经得到了较为广泛的应用[63-64]. 在铰接式车辆的路径跟踪控制中，孟宇等采用将预瞄误差加入优化目标的方法提出了前馈-LQR 路径跟踪控制器，一定程度改善了铰接式车辆跟踪曲率变化幅度较大的参考路径时的性能[18]. 但是受限于预瞄距离的设置，前馈-反馈控制器在参考路径包含不同幅度的曲率突变时仍然误差较大.

B. 模型预测控制

模型预测控制也是一种最优控制，MPC 与最优控制的关系如图1 所示. MPC 通常也会被称为后退时域控制（Receding horizon control，RHC）、滚动时域控制（Moving horizon control，MHC）等[65].MPC 在路径跟踪控制中的应用十分广泛，其原理是基于移动装备的数学模型建立预测模型，然后通过预测模型基于当前的位姿状态和所有可行的控制输入预测未来所有可能的位姿状态，接着通过优化目标函数找出其中与参考状态最为接近的位姿状态，进而得到该状态对应的控制输入. 由于在引入参考状态时，可以加入参考路径的变化趋势等信息，所以MPC 跟踪复杂参考路径的能力显著优于其他控制方法. 而且在确定控制输入的可行范围时，可以加入系统的约束条件，所以MPC能够显式地处理系统约束，从而获得相对其他控制方法十分显著的优势.

图 1 MPC 与最优控制的关系Fig.1 Relationship between MPC and optimal control

在2012 年至2015 年，Nayl 等提出了一种基于切换模型预测控制（Switching-MPC，SMPC）的铰接式车辆路径跟控制器，并证明了SMPC 的性能优于LQR 和基于极点配置（Pole placement，PP）的反馈线性化控制[24-26]. 考虑到该控制器的预测模型是由铰接式车辆的运动学模型推导获得的线性误差模型，所以SMPC 是一种线性MPC（Linear MPC,LMPC）. 在2019 年，孟宇等提出了基于线性时变MPC（Linear time varying MPC, LTV-MPC）的铰接式车辆路径跟踪控制器[66]，这种控制方法也是一种典型的LMPC.

上述LMPC 是一种采用当前误差预测未来误差的控制方法，当参考路径存在较大幅度的曲率突变且铰接式车辆的纵向行驶速度较高时，预测获得的未来误差和实际的未来误差之间偏差较大，所以在这种情况下LMPC 控制器的精确性仍然不足[10]. 非线性MPC（Nonlinear MPC, NMPC）在跟踪存在大幅度曲率突变的参考路径时相比LMPC性能更佳，因此白国星等提出了一种基于NMPC 的铰接式车辆路径跟踪控制器[10]和一种基于NMPC的铰接式车辆反应式导航运动控制器[67]，取得了相比LMPC 控制器更加精确的控制效果. 不过NMPC 控制器的计算成本较高，所以其实时性还有待进一步优化.

综合上述研究现状可知，在有前馈信息的路径跟踪控制方法中，MPC 能够有效引入参考路径的前馈信息，而且无需考虑预瞄距离的设置等问题，此外MPC 在处理系统约束方面也具有十分显著的优势，所以MPC 有助于提高铰接式车辆路径跟踪控制在参考路径存在较大幅度曲率突变时的精确性. 而在现存的多种MPC 中，NMPC 能够更加充分地利用参考路径的前馈信息，在铰接式车辆等工作环境狭窄的移动装备的路径跟踪控制中具有较为广泛的应用前景.

3 NMPC 路径跟踪控制方法

白国星等在对基于MPC 的路径跟踪控制进行回顾和比较时发现，目前存在两种NMPC 控制器设计思路，一种是以离散化后的运动学模型作为预测模型的典型NMPC 设计方法，另一种是以离散化后的非线性误差模型作为预测模型的非线性误差MPC（Nonlinear error MPC, NEMPC）[68]，各种MPC 的关系如图2 所示，下文中的NMPC 专指典型NMPC.

图 2 MPC 及其分支Fig.2 MPC and its branches

在文献[68]中，白国星等比较了NMPC 与NEMPC在移动机器人路径跟踪控制中的性能，但是移动机器人的运动学特性较铰接式车辆较为简单，因此对于这两种控制方法在铰接式车辆路径跟踪控制中的性能目前还未进行比较. 将式（3）中的模型代入文献[68]中的NEMPC 控制器设计过程，即可建立基于NEMPC 的铰接式车辆路径跟踪控制器.NMPC 控制器的设计过程则可以参考文献[10]和[69].为了保证比较的一致性，两个控制系统中铰接式车辆和控制器的参数均一致，如表1 所示.

表 1 铰接式车辆和控制器参数Table 1 Parameters of the articulated vehicle and controllers

参考路径为直线和圆弧组成的路径. 其中圆弧路径的半径为15 m，仿真起点的坐标为（20, 80）.参考速度设置为4 m·s-1时，仿真结果如图3 所示.图4 所示为仿真结果的局部放大. 图5 和图6 显示了横向误差和航向误差. 图7 显示了控制器在每个控制周期内的运算时间.

图 3 NMPC 和NEMPC 的仿真结果Fig.3 Simulation results of NMPC and NEMPC

图 4 NMPC 和NEMPC 的仿真结果局部放大Fig.4 Partial enlargement of simulation results of NMPC and NEMPC

图 5 NMPC 和NEMPC 的横向误差Fig.5 Lateral error of NMPC and NEMPC

图 6 NMPC 和NEMPC 的航向误差Fig.6 Heading error of NMPC and NEMPC

图 7 NMPC 和NEMPC 的运算时间Fig.7 Computation time of NMPC and NEMPC

根据仿真结果可知，NEMPC 在精确性方面逊色于NMPC. 而在实时性方面，NEMPC 的平均运算时间和最大运算时间小于NMPC 的平均运算时间和最大运算时间，但是NEMPC 的最大运算时间大于控制周期，所以它的实时性同样有待进一步优化.

总之在参考路径存在较大幅度的曲率突变时，NMPC 精确性显著优于NEMPC，与文献[68]中得到的结论一致，由此可知该结论不受被控平台运动学特性的影响. 至于在参考路径存在较大幅度的曲率突变时NEMPC 误差较大的原因，与文献[10]中LMPC 误差较大的原因类似. NEMPC 也通过当前误差预测未来误差，它与LMPC 的区别仅为预测的迭代过程中保留了非线性项.

接着继续分析NMPC 的性能. 通过图5 和图6可知，NMPC 在跟踪直线路径时误差较小，而参考路径在直线和弯道之间切换时，即参考路径存在较大幅度的曲率突变时，横向误差和航向误差均有所增大. 因此可以合理推断，当参考路径的曲率突变幅度更大时，路径跟踪控制将产生更大的误差. 此外当基于NMPC 的铰接式车辆路径跟踪控制器以不同的参考速度跟踪上述参考路径时，可以得到不同的横向误差最大值和航向误差最大值. 随着参考速度的增加，误差最大值也会出现增加的趋势. 当其他参数与上述仿真一致时，NMPC的误差最大值变化趋势如图8 所示.

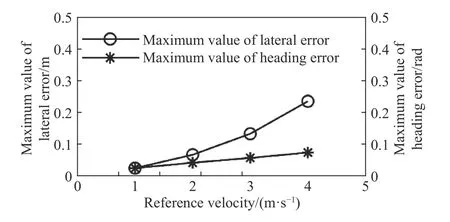
图 8 NMPC 的误差最大值随参考速度变化趋势Fig.8 Change trend in maximum error of NMPC with reference velocity changes

由此可知，在参考路径存在较大幅度的曲率突变以及参考速度较高时，虽然基于NMPC 的铰接式车辆路径跟踪控制器较基于其他控制方法的控制器精确性较高，但是这种控制器仍然存在继续改进的余地.

针对上述问题，至少存在两种解决思路. 第一种思路是继续改进NMPC，白国星等在针对移动机器人的路径跟踪控制中发现NMPC 的优化目标和参考速度之间存在耦合关系[70]，针对该耦合关系进行解耦研究，能够进一步提高在参考路径存在较大幅度曲率突变时的路径跟踪控制精确性.第二种思路是加入速度决策控制器，白国星等提出了一种结合NMPC 和LMPC 的多层MPC（Multilayer MPC, MMPC）路径跟踪控制器. 这种控制器采用能够在更长的预测时域精确预测铰接式车辆位姿的NMPC 控制器作为速度决策控制器，采用实时性更好的LMPC 控制器作为底层路径跟踪控制器，从而实现了通过动态调节纵向速度进一步提高路径跟踪控制精确性的目的[71]. 不过在路径跟踪控制系统存在较大幅度的定位误差时，MMPC控制下的铰接式车辆可能会陷入低速行驶的状态，因此这项工作还需进一步完善.

目前，基于NMPC 的铰接式车辆路径跟踪控制存在的另一个问题是预测模型仍然以运动学模型为基础. 在铰接式车辆以较低的参考速度（如5 m·s-1以下）运行时，以运动学为基础的NMPC 路径跟踪控制系统性能较好，但是在铰接式车辆以较高的参考速度（如10 m·s-1以上）运行时，侧向速度导致的精确性下降和安全性恶化的问题必须被纳入考虑. 研究者们针对移动机器人的研究[70]和针对乘用车等移动装备的研究[72-76]表明，以动力学模型作为预测模型的基础可以有效解决这个问题. 因此基于NMPC 的铰接式车辆路径跟踪控制的一个重要发展方向，就是建立以动力学模型为预测模型的控制器，提高铰接式车辆以较高参考速度运行时路径跟踪控制的精确性.

此外，根据前文中的仿真结果可知，目前基于NMPC 的铰接式车辆路径跟踪控制器还面临着实时性方面的挑战. 随着计算机硬件性能的飞速进步，实时性问题已经不再是限制NMPC 路径跟踪控制方法应用的瓶颈，本文仿真中使用的计算机处理器仅为Intel（R）Core（TM）i5-8500 @ 3.00 GHz，如果采用性能更强的处理器，NMPC 在实时性方面的表现必然会有所提升，但是出于成本控制的考虑，实时性方面的优化仍然是基于NMPC 的铰接式车辆路径跟踪控制领域中的一个重要发展方向.

4 结论与展望

从铰接式车辆数学模型和铰接式车辆路径跟踪控制方法两个方面，回顾了矿用铰接式车辆路径跟踪控制关键研究点的现状和进展，并得出了以下结论与展望：

（1）在数学模型研究中，铰接式车辆的无侧滑经典运动学模型在行驶速度较低时精确性较高，完全能够满足铰接式车辆低速路径跟踪控制的需求，可以作为低速路径跟踪控制的参考模型. 而有侧滑运动学模型在低速时性能与无侧滑经典运动学模型相近，高速时则存在可能增大侧滑趋势的问题. 在动力学模型层面，目前基于牛顿-欧拉法建立的铰接式车辆四自由度动力学模型原则上能够满足路径跟踪控制的需求，但是目前存在的四自由度模型无法同时反映铰接式车辆的瞬态转向特性和稳态转向特性，还需要继续加以改进.

（2）在路径跟踪控制方法研究中，传统的无前馈信息控制方法，如反馈线性化控制、最优控制、PID 控制、SMC 等，均无法有效解决铰接式车辆跟踪存在较大幅度曲率突变的参考路径时误差较大的问题. 基于上述反馈控制提出的前馈-反馈控制可以用于解决上述问题，但是受限于预瞄距离的设置，前馈-反馈控制器在参考路径包含不同幅度的曲率突变时仍然误差较大，在后续的研究中可以通过自动调整预瞄距离进一步提高前馈-反馈控制的精确性. MPC 是另一种引入前馈信息的控制方法，这种控制方法可以更加有效地利用前馈信息，且不需要考虑预瞄距离的设置. 而在目前存在的多种MPC 中，NMPC 较LMPC、NEMPC 等方法在跟踪存在较大幅度曲率突变的参考路径时精确性更高

（3）对于基于NMPC 的铰接式车辆路径跟踪控制，目前仍然存在三方面的问题. 首先，这种控制方法仍然存在误差最大值随参考速度增大而增加的趋势. 这个问题可以通过对NMPC 进行解耦研究和增加速度决策控制器来解决，但是目前尚未出现成熟的研究成果. 其次，目前基于NMPC 的铰接式车辆路径跟踪控制仍然以运动学模型作为预测模型的理论基础，从而无法解决铰接式车辆以较高的参考速度运行时侧向速度导致的精确性下降和安全性恶化的问题. 这个问题需要通过建立以动力学模型为预测模型的路径跟踪控制器来解决，因此必须加紧研究面向路径跟踪控制的铰接式车辆动力学模型. 最后，这种控制方法仍然面临着实时性方面的挑战，所以还需对该控制方法进行实时性优化研究.