用环状阵列式透镜板实现平顶声压
谷成富,王 华*
(1.超声医学工程国家重点实验室 重庆医科大学生物医学工程学院,重庆 400016;2.重庆市生物医学工程学重点实验室,重庆 400016)
引言
在声学领域,能量均匀分布的平顶声场存在着广泛的应用价值,如,用于工业无损检测的超声全息,为了获得更好的成像质量,通常选择面积较大的换能器工作在近场区以获得近似均匀的声场。[1-2]在现有的超声回波成像中,人们往往忽略了声场均匀性对于增强成像可靠性的作用。在超声生物学效应的研究中,声场的不均匀性也会使同一区域不同位置的观察结果出现一定的差异,给研究者探究超声以外的因素分析带来干扰。
然而目前几乎都是用平面超声的近场区来近似代替均匀声场,缺乏针对产生均匀声场的相关设计。理论上,相控阵超声换能器能实现任意声压分布的声场模式,不过其相移系统昂贵,制作工艺复杂,难以在实际应用中普及。[3]最近新出现的声学超表面,对离散化的相位设计出对应的单元构成的阵列,能将波前塑造成期望的形状,但其设计和实现条件较为苛刻,也存在入射波前和目标波前之间阻抗失配带来的低效等问题。[4-5]声透镜具备与平面压电陶瓷结合可用的灵活性以及制造成本较低等优势,成为我们研究的主题,传统的声透镜设计主要依赖于弯曲曲面或改变整个体积的折射率以实现聚焦超声或波束转向,对于实现平顶声场的透镜研究较少。[6-9]探究出一种用透镜实现平顶声场的方法具有重要科学价值和实际意义。
声透镜作为典型的相位调控元件,其输入面的声场振幅通常呈均匀分布,在满足输入面和输出面之间波传输关系的条件下,找出输入面上声场适当的相位分布,使得输出面上的振幅分布为平顶分布就能完成透镜的设计。基于这一思想,本文基于惠更斯原理的瑞利积分法为基础协同模拟退火粒子群算法,提出用环状阵列式透镜板来实现平顶声压,该设计方法无需构造复杂的衍射分析模型,也不涉及利用等效参数模型完成对应透镜材料参数的配置,方式简单,灵活。同时,该方法将在很大程度上迎合当前科技工作者在实际应用中遇到的逆向设计问题,因此我们的工作不仅在于设计出简单结构的平面声学设备来实现平顶声压,也为解决一些逆向设计问题提供了解决方案参考。
1 实现平顶声压分布的透镜板设计原理
当透镜输入面作均匀振动时,在忽略声衰减的情况下,振动源在声场中某点产生的复声压pm=aeiφ可以用基于惠更斯原理的瑞利积分法表示:[10-11]

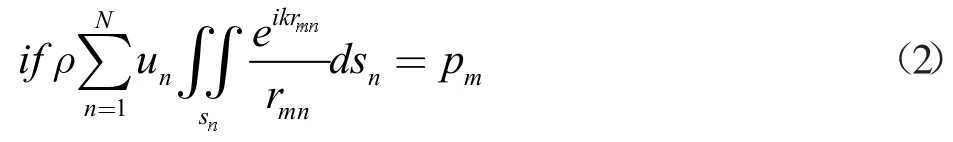
式中un和sn分别为阵列中第n 个单元的输入声场复压和振动源面积,rmn为振动微元dsn中心到场点m 的距离。那么声场中场点m=1,2,3,…,M 的复声压可以用矩阵的形式表达为:

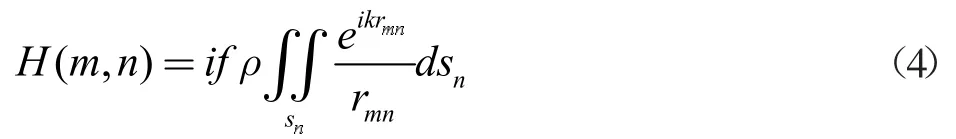
对于一块给定厚度的透镜圆板,将其声场输入面划分为N 个环形辐射单元,与输出圆面构建空间关系如图1 所示。
圆对称划分的优势在于只需获得输出圆面上过圆心任意直线上的声压分布,就能获得整个圆面上的声压分布,为计算方便选择图中的A 直线为计算直线。空间关系一旦建立,前向传输算子H 就得到确定,如果期望计算直线上振幅分布am为平顶分布ad,接下来就是需要找出输入面声场上适当的相位分布φn,使得HuN的振幅分布接近平顶分布。为了描述HuN振幅与ad的接近程度,引入一个量E,其定义为:
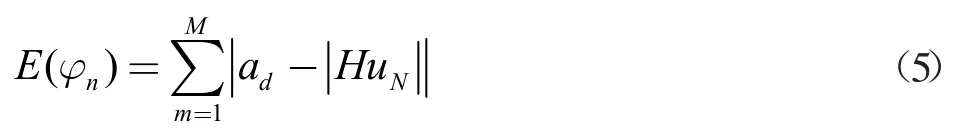
如果E=0,则能完美找出输入面声场相位分布φn。在这里我们将模拟退火粒子群算法引入到最优φn的寻找中,以使得E 小于给定的误差。
算法的寻优过程通俗来讲就是随机生成一定数量的初始解,每个初始解既代表一组相位分布φn,然后各个初始解并行进行不断的扰动变化,每次扰动变化的方向由原行方向,当前自身最优解方向和当前全局最优解(退火机制和轮盘赌选择法的引入将会改变全局最优解的位置)方向决定,如果原解经过一次扰动变化后生成新解的E 小于原解的E,则新解将会替代原解,反之新解将会被舍弃原解得到保留,经过不断迭代后,当全局最优解满足预设的精度即可获得较优的相位分布,具体算法步骤详见参考文献[12]。
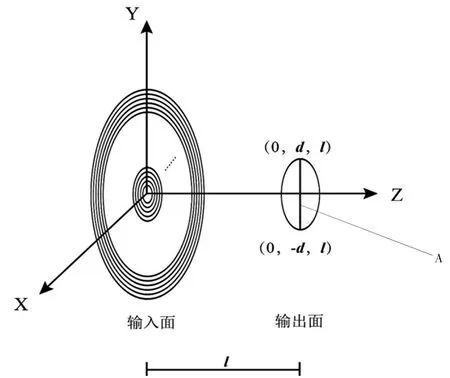
图1 输入面与输出面空间关系示意图

图2 全局最优解对应的E 迭代曲线
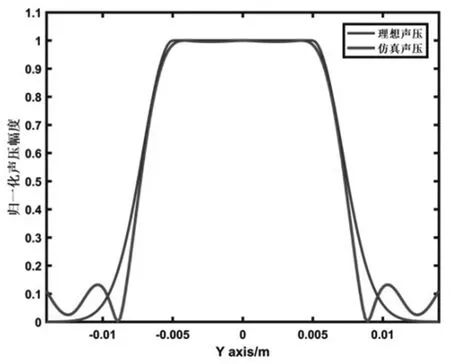
图3 理论仿真声压与理想平顶声压比较
2 结果
本文在理论仿真中,选取传播媒质为水,声速c1为1500m/s,密度 ρ 为 1000kg/m3,超声频率 f 为 1MHz。声场输入面划分参数:半径为R=0.06m 的辐射圆面划分为n=149 个等宽度为0.0004m 的环形带,中心圆的半径为0.00045m,声场输入面与输出圆面的水平距离l=0.208m,观察区域半径d=0.014mm。算法中最大迭代数定为400,学习因子β1和β2均取2.05,粒子群规模设为60,退火系数取0.5,运算精度要求:全局最优解的误差小于10。
经计算得到的迭代曲线如图(2)所示。
从图中可以看出,运用模拟退火粒子群算法能够使E 较为快速的收敛到误差极小值8.188,将全局最优解代入Hun中得到计算直线上的理论声压分布,同时与构造的理想平顶声压分布相比,如图(3)所示。可以看出计算直线上的仿真声压分布接近于能量均匀分布的理想平顶声压,两者间均方误差为0.0044,属于较为理想的结果。
又由于辐射面属于圆对称分割,将图(3)中的仿真声压绕其对称中心二维旋转,既能得到整个输出圆面上的声压分布,如图(4)所示。最后可以根据声程差与相位延迟之间的关系以及所选的声透镜材料将各环单元的相位转换为透镜的深度分布,为透镜的加工提供理论支持。[13]

图4 输出圆面上的二维声压分布
3 结论
本文提出一种环状阵列式透镜设计用于产生平顶声压,将经透镜调制后的相位分布寻找与基于模拟退火粒子群算法联系起来,通过仿真在空间特定输出区域获得了平顶声压分布,结果与构造的理想平顶声压分布相比符合较好。不足之处在于,由于受到透镜精密加工的条件限制,该透镜目前只停留于理论仿真阶段。总体来说,本文所提透镜设计方法可以为透镜的加工提供理论依据,具有一定的实际意义。平顶声压分布的实现,具有促进超声应用范围扩大的潜力,加速声学技术的发展。

