地铁通道行人流交通特性分析
庄子翌
(西安公路研究院,陕西 西安 710000)
引言
行人交通特性是指行人作为群体表现出来的宏观特性,行人宏观交通特性用速度、密度、流率三个基本参数来表征,描述交通流三参数基本关系的图像称为基本图。本文研究的交通流参数特性主要包括两方面:一是交通流参数随时间的变化特性,即交通流参数的时变特性,二是交通流参数之间的相互关系特性。
关于交通枢纽内换乘通道的行人交通特性,国内外学者采用视频调查法进行了大量研究。William H. K. Lam[1]研究了香港走行设施的行人速度/流量关系;徐蔷薇[2]对水平通道上不同性别与通道坡度的乘客步速分布进行调查与拟合,得到水平通道上步速-个人空间关系曲线;周继彪[3]通过设计数据采集试验定量研究枢纽内水平通道处行人流量、速度、密度和空间占有率之间的相互关系;王飞[4]通过视频调查数据拟合得到单向换乘通道流量和走行速度的关系,进而得到单向换乘通道自由流下的走形时间;杨丽丽[5]通过实测数据对水平通道行人流基本模型进行修正;刘立元[6]利用实测数据拟合得到双向水平通道上行人步频、步幅、步速的相互关系等,但缺少Y 型换乘通道内行人流交通特性研究。目前Van Aerde 模型多应用在道路交通,WuNing 等[7]应用串联-排队论理论考虑道路上连续车辆的相互关系来推导Van Aerde 模型;赵娜乐等[8]利用Van Aerde 交通流模型对北京市三环快速路典型路段的交通流参数进行了标定,并对比分析了不同天、内外环及不同车道的交通流特性。邹娇等[9]对经典Van Aerde 模型进行推导,并标定了合肥市城市主干路的Van Aerde 模型。陈大山等[10]基于实测数据建立占有率与密度的关系,并采用遗传算法与最小二乘法对快速路Van Aerde 模型进行标定,但目前尚未有Van Aerde 模型在行人交通流方面的应用研究。本文以Y 型通道内行人交通流实测数据为基础,描述通道内行人交通特性,并利用绘制的交通流参数基本图标定Van Aerde 模型,建立行人流速度-密度关系模型。
1 调查准备

图1 数据采集及处理示意图
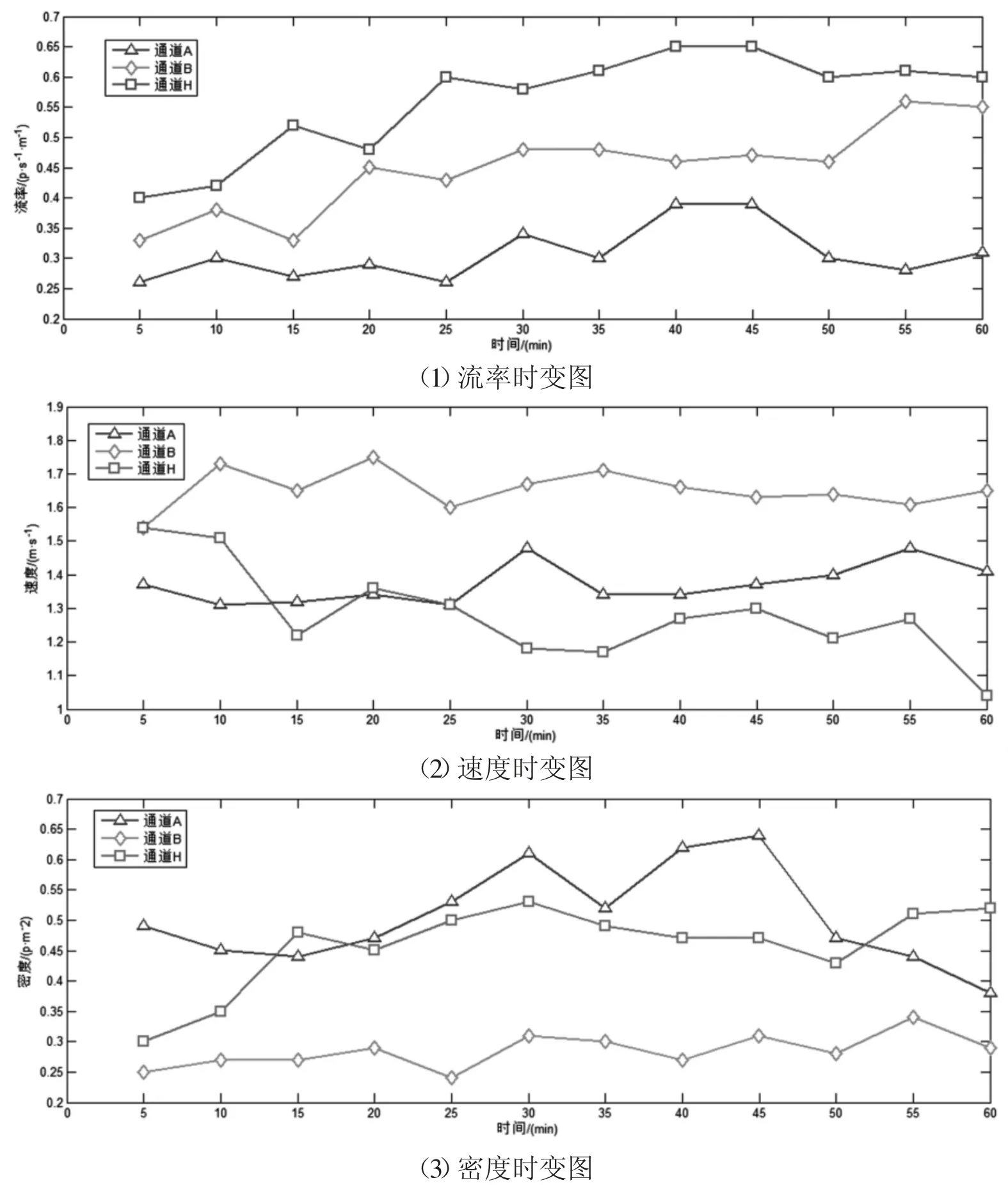
图2 以5min 为时间间隔的各通道交通流参数时变图
本文基于北京市西直门地铁站历史数据,选择周五早高峰为调查时段(7:30~8:30),采用视频调查法观测Y型单向换乘通道分支及汇集处典型区域的高峰小时行人步行状况。本文以流率、速度、密度为参数来研究行人流的宏观交通特性,以10s 为时间间隔对视频资料中行人交通流三参数的数据进行统计处理,数据采集及处理示意图如图1 所示。
1.1 行人交通流率(V)
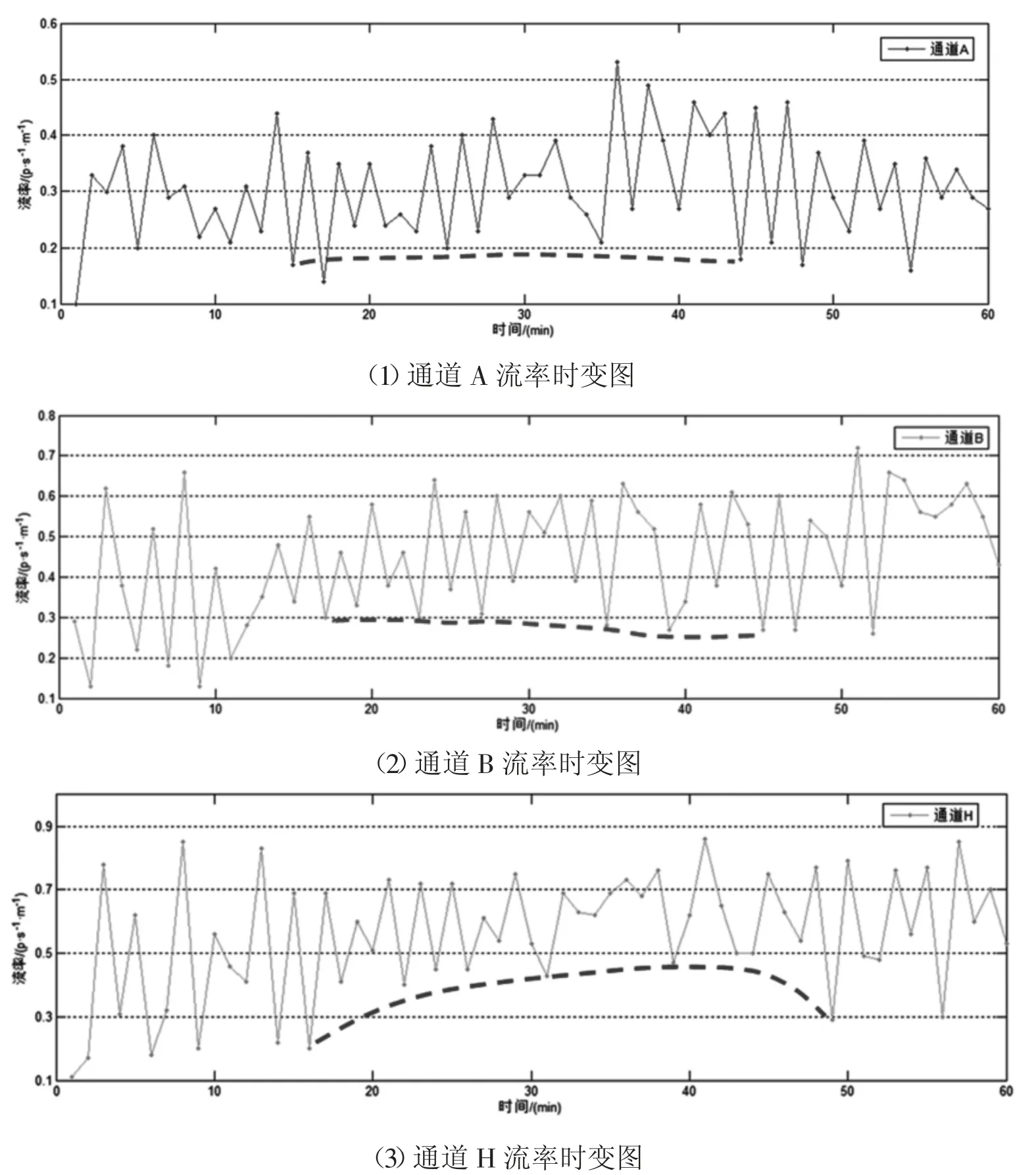
图3 以1min 为时间间隔的各通道流率时变图
指单位时间间隔单位宽度内通过换乘通道某一断面的行人数,单位为p/(s·m),数据处理方法是记录某时间间隔内通过研究区域内单位宽度某断面的行人数。
1.2 行人密度(K)
指某个瞬间通道内单位面积或研究区域上存在的行人数量,一般数据处理方法是统计某一时刻末停留在调查区域内的行人数量,然后除以调查区域的面积(L×W)。
1.3 行人速度(U)
指行人流的空间平均速度,即某一时间段内行人通过通道一段距离的平均值,一般处理方法是记录视频中给定范围内不同行人进入观测区域和离开观测区域的准确时间(t1,t2),并根据第i 个行人在观测区域内的步行长度(xi2-xi1)计算行人的步行速度。
2 交通流参数的时变特性
Y 型通道行人交通流的时变特性就是指行人交通流基本参数:流率、速度、密度随时间的变化特性。将数据处理结果分别以 5min、1min、30s、10s 为时间间隔绘制交通流参数时变图,观察各参数随时间的变化规律,并对比不同通道内行人交通特性的异同。
2.1 以5min 为时间间隔可看出通道内行人交通流总体变化趋势
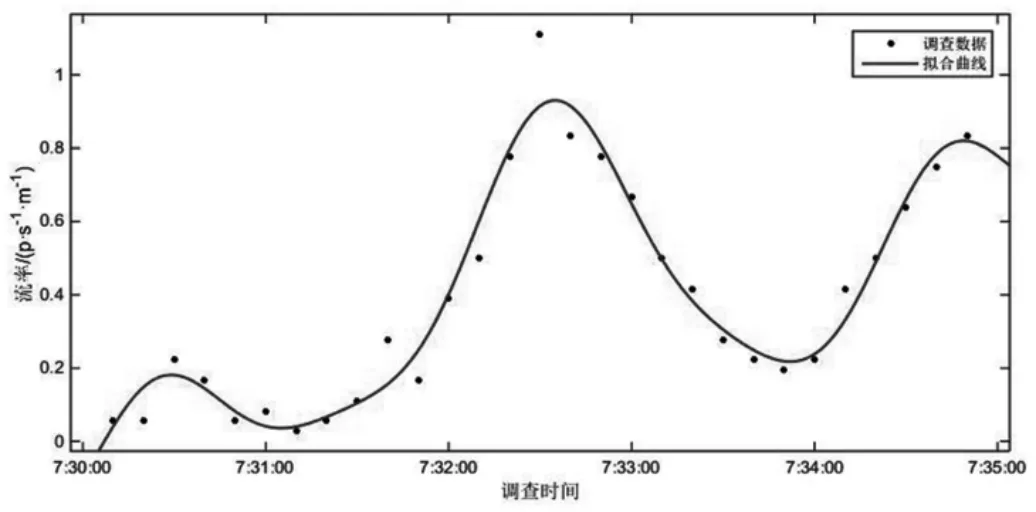
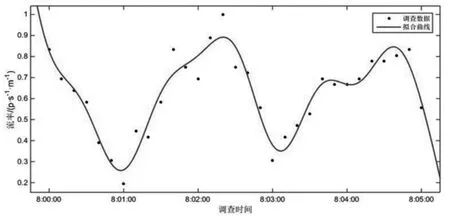
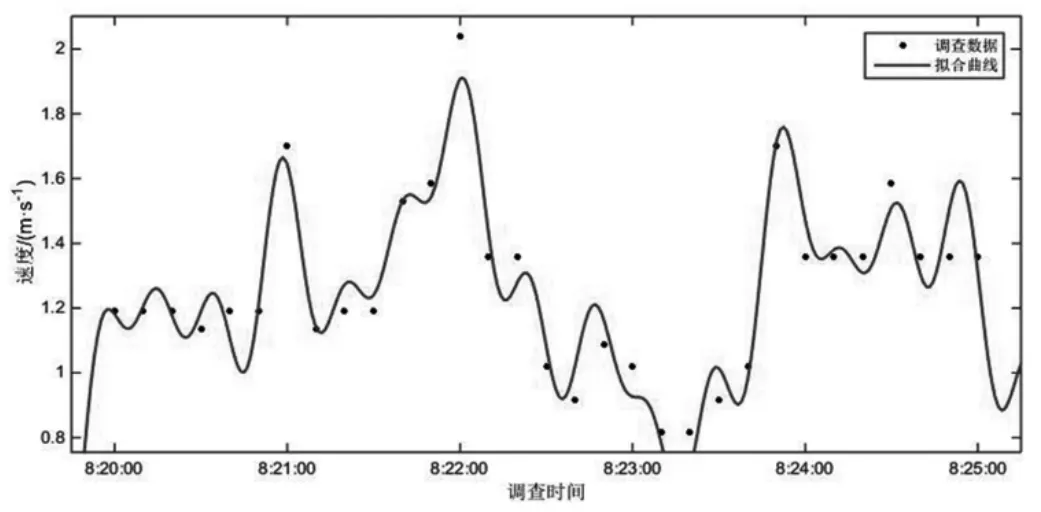
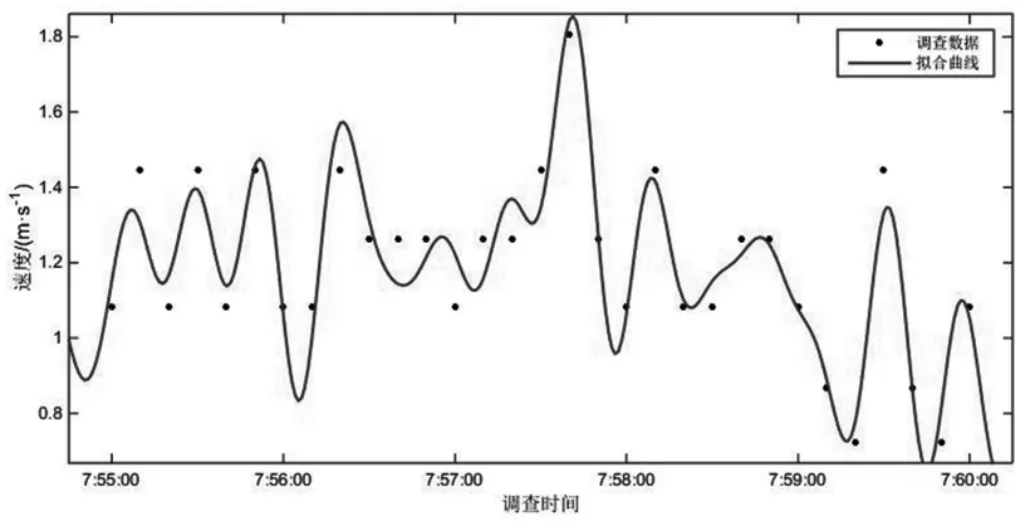
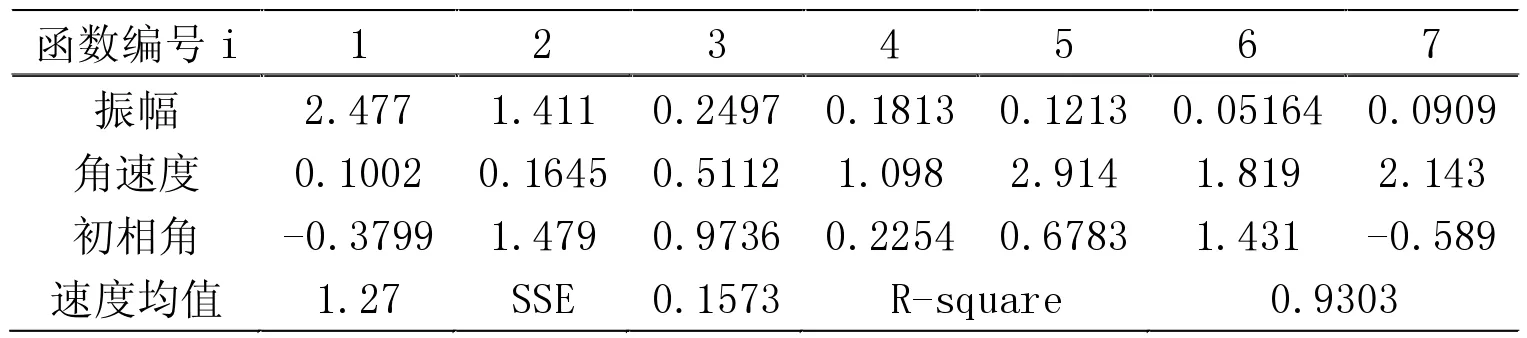
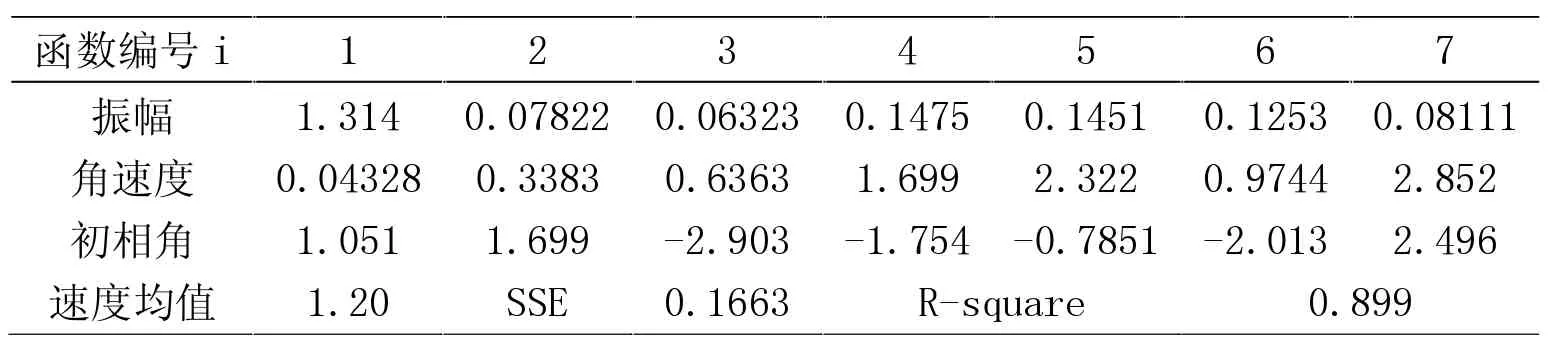
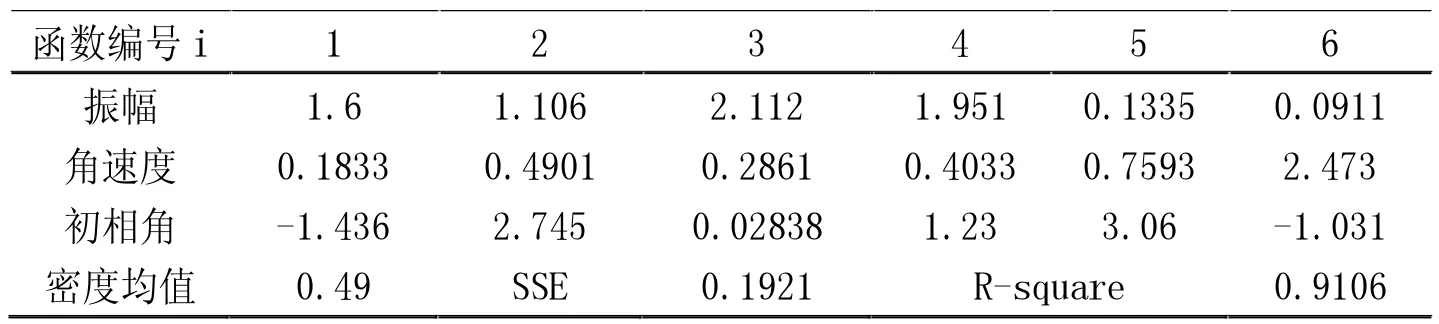
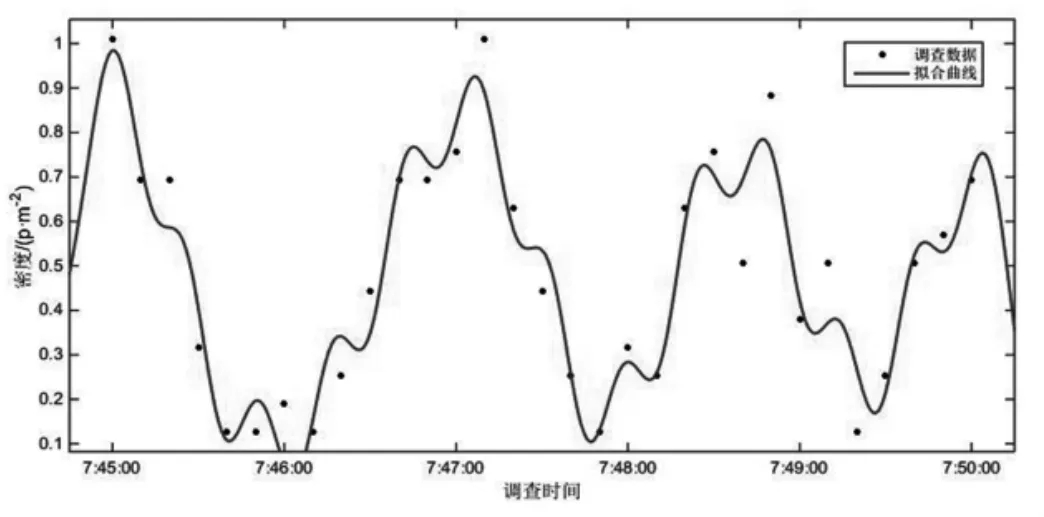
以5min 为时间间隔的交通流参数时变图(图2)显示,调查期间所选通道各分支行人交通量相差较大,大小关系为VH>VB>VA。其中,流率时变图前30min(自由流状态下)内分支通道与汇集通道行人流率变化状态相反,分支通道流率下降时,汇集通道流率处于上升趋势,说明了通道内交通波的传播及延迟性。汇集处交通量为各分支交通量在该点的叠加,叠加的交通量大小和叠加时间与通道的长度及行人的走行速度有关,而30min 后(拥挤状态下),通道内行人密度较大,相互干扰,行人受到周边行人的影响不能按自由意愿行走,交通波的传播受到影响。结合行人速度时变数据可以看出,当流率增加时速度先增加后减小,即UB>UA>UH。由于通道A、H 调查地点选择通道入口处,通道B 选择通道中部,因此行人密度关系为KA>KH>KB,KH 图4 以1min 为时间间隔的各通道密度时变图 行人步行速度随自身条件及外界环境影响会发生突变,数据存在不稳定性,相比之下,流率和密度数据变化趋势更稳定,更能显示出拥挤前后的状态转变过程,因此选择流率和密度数据进行对比绘制时变图。 图5 各通道速度分布直方图 表1 行人平均速度表 以1min 为时间间隔的流率、密度时变图(图3、图4)显示,分支通道A、B 内的行人交通流未发生拥挤现象,随着列车到发,通道内行人流率和密度发生周期性波动变化,波峰和波谷分布均匀,而汇集通道H 中行人流率和密度的时变图能明显显示出平峰与高峰的转变过程,行人流由非拥挤向拥挤状态逐渐过渡,在15min 处流率和密度开始快速上升,波峰波谷的变化率逐渐减少,在30~40min 处流率和密度的波峰达到最大值,变化率最小,此时通道内行人处于拥挤状态,40min 后波谷明显开始下降,拥挤状态开始消散,高峰期逐渐过去,流率和密度整体呈现先增加后减小的趋势。 将速度数据以30s 为时间间隔进行统计处理,汇总得到行人速度平均表(表1),并以频率百分数为纵轴,速度为横轴绘制Y 型通道不同分支及汇集处速度分布直方图如图5 所示。行人在Y 型通道内的平均速度符合正态分布,通道A、B、H 的速度平均值分别为1.37m/s、1.65m/s 和1.28m/s,说明通道中段的行人速度大于入口处的行人速度,且速度随流量的增加先增加后减小。 根据国内外研究,美国纽约地铁站内行人在水平通道内的速度符合正态分布,平均走行速度为1.4m/s,大于其他环境的速度。一项针对北京地铁西直门站的行人交通数据调查显示,出口通道行人速度变化范围男性为1.84~0.9m/s,女性为1.68~1.05m/s,换乘通道行人速度变化范围男性为1.93~1.02m/s,女性为1.96~0.98m/s[11],与本文调查结果类似,本文将速度分布区间更加细化。 行人交通流参数时变图显示,随着地铁列车的到发,Y 型通道内行人流呈现出急剧升高的特性,这种状态持续一段时间(与列车到发间隔相关)后,通道行人流率逐渐减少,下趟列车到来后,这种现象既而复现,因此Y 型通道各分支与汇集通道处行人交通流参数可能存在某种周期性变化趋势。本文对以10s 为时间间隔的调查数据每5 分钟一组采用正弦函数进行周期性拟合,以SSE 趋近于0,R2接近于1 的次数最低为目标,拟合结果证明了这一特性,同时显示流率的数据拟合度最高,其次是密度,速度的拟合度最低,主要因为行人的速度突变性较强。在Y 型通道中,汇集通道H 的数据拟合度较通道A、B 更高,且拟合次数更低,自由流状态较拥挤状态拟合度更高。限于篇幅,本文以通道H 拥挤状态和自由流状态数据拟合图形为例来说明行人交通流三参数的波动特性。 平滑曲线为正弦函数拟合曲线,拟合通式如下: 式中:ai为振幅;bi为角速度;ci-初相角;x 为时间间隔;n 为正弦函数数目。 交通流参数之间的相互关系特性用行人交通流基本图表示,该图描述了速度、流率、密度三个参数之间的关系,同时也反映了行人交通流从自由到拥挤、从稳定区到非稳定区的过程[11]。根据交通流理论,得到交通流三参数关系模型如图12 所示。完整的行人交通流基本图包括如下特征值:通行能力、自由流速度、临界速度、能力密度和拥挤密度。 图6 通道H 自由流状态流率波动特性 表2 通道H 自由流状态流率数据波动性拟合函数参数取值 图7 通道H 拥挤状态流率波动特性 表3 通道H 拥挤状态流率数据波动性拟合函数参数取值 图8 通道H 自由流状态速度波动特性 图9 通道H 拥挤状态速度波动特性 图10 通道H 自由流状态密度波动特性 由图12 中可以看出,行人流具有自由流和拥挤流两种交通状态。vf为自由流速度,其值为流率曲线在密度为0 处的斜率,此状态下行人根据自身意愿自由行走无相互影响。随着行人流率增加,密度也逐渐增加,当q=qc时,流率达到最大值,该值可用于描述步行交通设施的通行能力,此时对应能力密度kc和临界速度vc,当密度超过能力密度kc时,流率开始下降,行人流的状态由自由流转变为拥挤流。当拥挤导致行人流率和速度均为0 时,此时的密度为拥挤密度kmax。 表4 通道H 自由流状态速度数据波动性拟合函数参数取值 表5 通道H 拥挤状态速度数据波动性拟合函数参数取值 表6 通道H 自由流状态密度数据波动性拟合函数参数取值 表7 通道H 拥挤状态密度数据波动性拟合函数参数取值 图11 通道H 拥挤状态密度波动特性 本文选择荷兰Van Aerde 提出的速度-密度模型,该模型结构简单,易于标定,通用性强。文章根据地铁Y 型通道各分支处采集到的行人交通流数据有针对性地完成Van Aerde 模型中交通流特征参数的标定,主要方法是:利用采集到的Y 型通道内研究区域的行人交通流数据,绘制交通流参数流量-密度关系散点图并对图像进行拟合,从而得到Van Aerde 模型中各交通流特征参数的值,将特征参数值带入变量表达式,即可求得c1、c2、c3的具体数值,从而得到研究区域的密度-速度关系函数。Van Aerde 模型由式(2)~式(5)组成。 式中:k 为密度(p/m2);vs为空间平均速度(m/s);vf为自由流速度(m/s);vc为临界速度,m/s;qc为通行能力(p/(s·m));kmax为阻塞密度(p/m2)。 通过对高峰时段Y 型通道行人流实际调查数据的处理,绘制各分支通道的流率-密度关系散点图,由图像知仅通道H 的流量-密度曲线近似通过原点,符合流率-密度的抛物线关系,因此对通道H 的流率-密度关系散点图进行二次多项式拟合,拟合结果如图13 所示,并得到Van Aerde 模型中各交通流特征参数的值。 根据汇集通道H 交通流特征参数的值,标定Van Aerde 模型的中间变量,得到适用于Y 型通道汇集处行人交通流的密度-速度关系模型如下式。 本文利用北京市地铁西直门站Y 型通道的行人调查数据,探讨Y 型通道内行人交通流参数的时变特性和相互关系特性,研究得到的结论如下: (1)以5min 为时间间隔绘制交通流参数时变图,描述各分支通道流率、密度、速度随时间变化的情况; (2)以1min 为时间间隔对比各通道流率、密度时变图,汇集通道的时变图可明显体现行人交通流由自由流状态向拥挤状态的转变过程; (3)以30s 为时间间隔绘制各通道速度、密度直方图,得到通道A、B、H 的速度平均值分别为 1.37m/s、1.65m/s 和1.28m/s,密度平均值分别为0.51p/m2、0.29p/m2和0.46p/m2; (4)以10s 为时间间隔对汇集通道自由流及拥挤状态下的行人数据进行正弦函数拟合,得到拟合图像及拟合函数参数取值; 图12 交通流三参数关系模型图 图13 通道H 流率-密度关系散点图拟合结果 (5)根据交通流基本图绘制Y 型通道汇集处的流量-密度散点图,对图像进行二次多项式拟合,并得到Van Aerde 模型中各交通流特征参数的值,带入变量表达式,求得Y 型通道汇集处的密度-速度关系函数。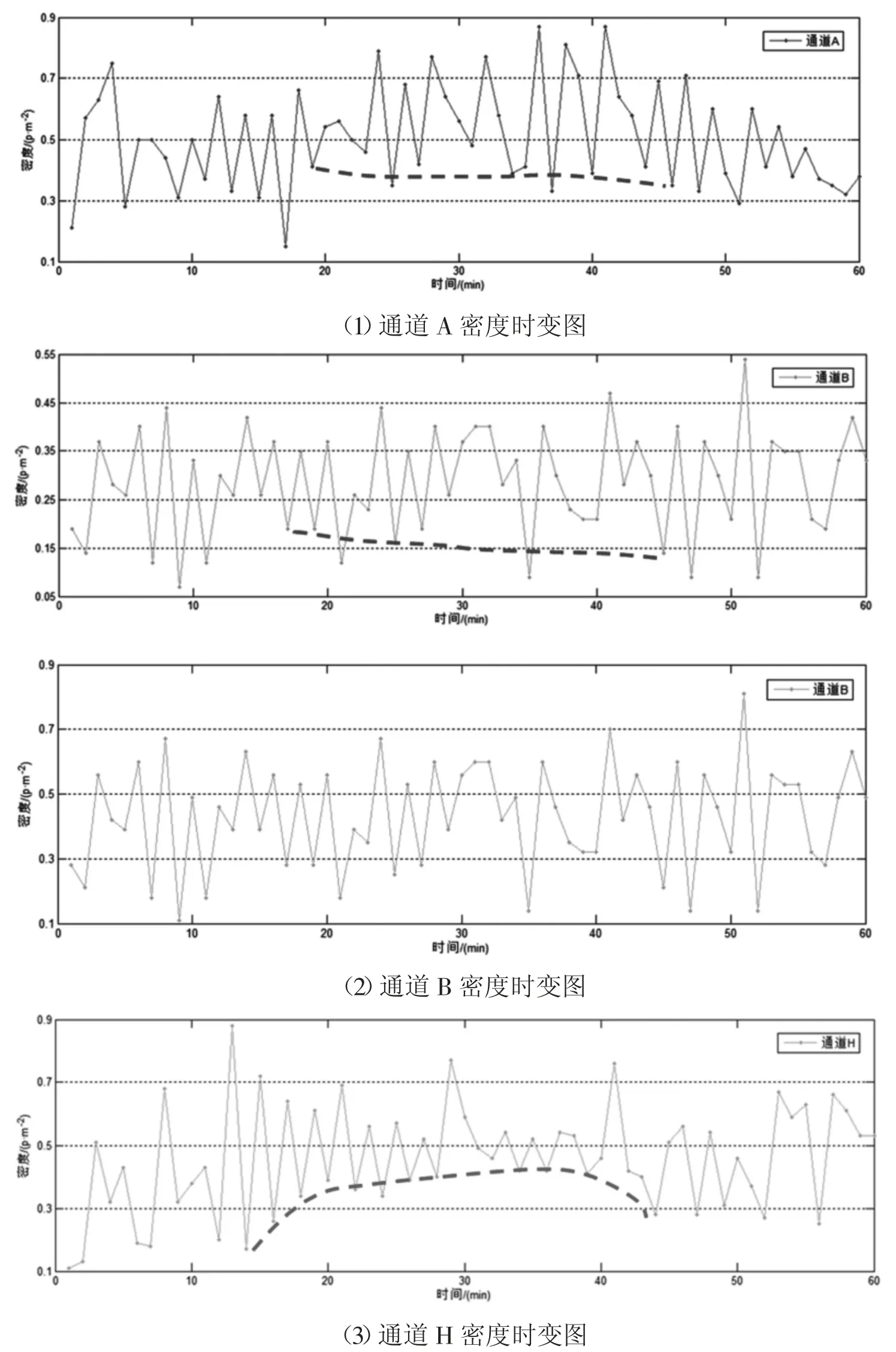
2.2 以1min 为时间间隔可看出通道内行人交通的状态转变过程


2.3 以30s 为时间间隔得到通道行人流速度频率直方图
2.4 以10s 为时间间隔可对通道行人流数据进行正弦函数拟合

3 交通流参数之间的相互关系特性
3.1 交通流基本图




3.2 Van Aerde 速度-密度模型
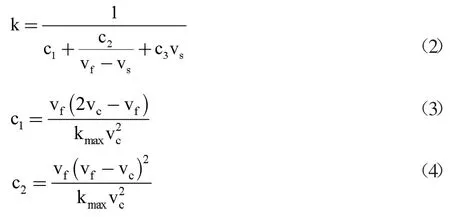

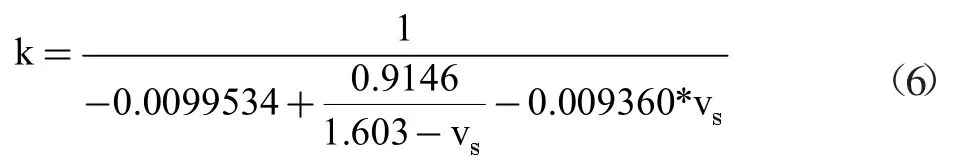
4 结论



